2024-2025学年湖南省耒阳市冠湘中学数学九年级第一学期开学达标检测模拟试题【含答案】

这是一份2024-2025学年湖南省耒阳市冠湘中学数学九年级第一学期开学达标检测模拟试题【含答案】，共22页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、（4分）下列图形具有稳定性的是（ ）
A．三角形B．四边形C．五边形D．六边形
2、（4分）如图，长方形ABCD中，BE、CE分别平分∠ABC和∠DCB，点E在AD上，①△ABE≌△DCE；②△ABE和△DCE都是等腰直角三角形；③AE=DE；④△BCE是等边三角形，以上结论正确的有( )
A．1个B．2个C．4个D．3个
3、（4分）在实数范围内，有意义，则x的取值范围是（ ）
A．x≥0B．x≤0C．x＞0D．x＜0
4、（4分）已知A（1，y1）、B（2，y2）、C（-3，y3）都在反比例函数y=的图象上，则y1、y2、y3的大小关系的是（ ）
A．y2＞y1＞y3B．y1＞y2＞y3C．y3＞y2＞y1D．y1＞y3＞y2
5、（4分）如图，的周长为，对角线，相交于点，点是的中点，，则的周长为（ ）
A．B．C．D．
6、（4分）已知：a=，b=，则a与b的关系是（ ）
A．相等B．互为相反数C．互为倒数D．平方相等
7、（4分）某单位向一所希望小学赠送1080本课外书，现用A、B两种不同的包装箱进行包装，单独使用B型包装箱比单独使用A型包装箱可少用6个；已知每个B型包装箱比每个A型包装箱可多装15本课外书．若设每个A型包装箱可以装书x本，则根据题意列得方程为（ ）
A．B．
C．D．
8、（4分）下列各组数中，可以构成直角三角形的三边长的是（ ）
A．1，2，3B．2，3，4C．1，，D．1，，3
二、填空题（本大题共5个小题，每小题4分，共20分）
9、（4分）若直角三角形的两直角边长为a、b，且满足，则该直角三角形的斜边长为 ．
10、（4分）已知关于的方程会产生增根，则的值为________．
11、（4分）因式分解：______.
12、（4分）一个等腰三角形的周长为12cm，设其底边长为y cm，腰长为x cm，则y与x的函数关系是为_____________________.(不写x的取值范围)
13、（4分）已知，则的值是_______．
三、解答题（本大题共5个小题，共48分）
14、（12分）解一元二次方程：
(1)6x2﹣x﹣2＝0
(2)(x+3)(x﹣3)＝3
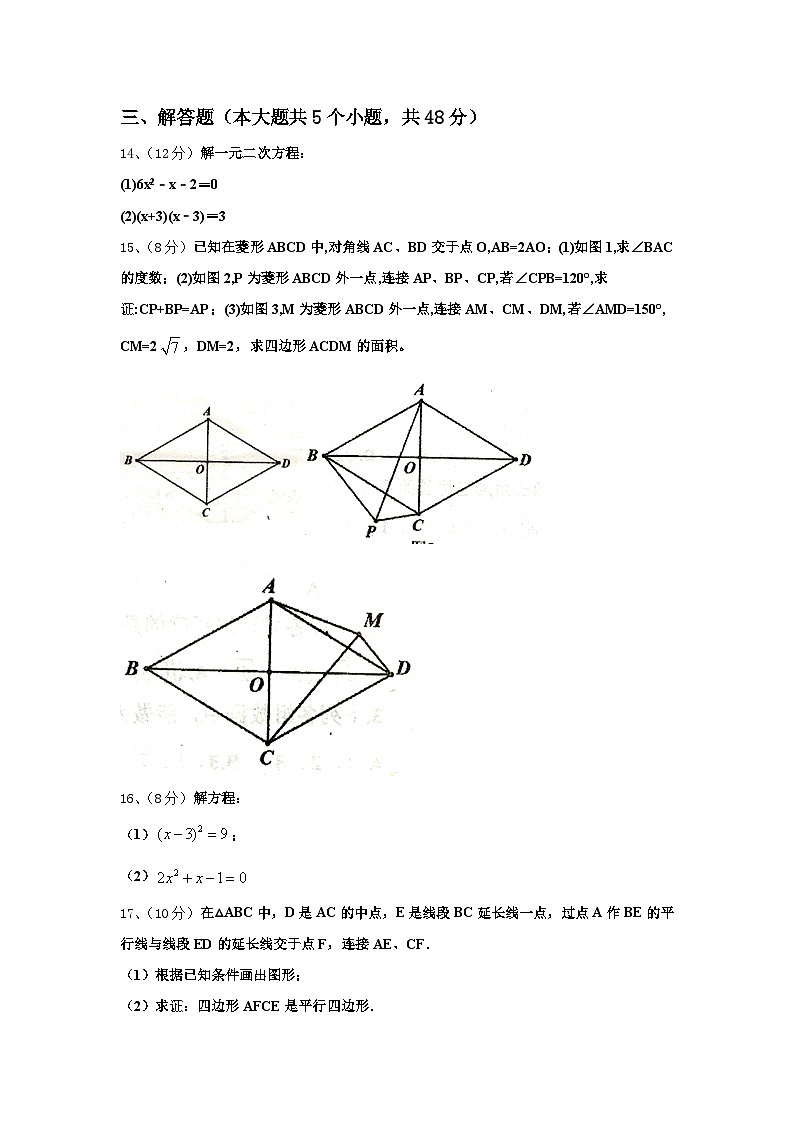
15、（8分）已知在菱形ABCD中,对角线AC、BD交于点O,AB=2AO；(1)如图1,求∠BAC的度数；(2)如图2,P为菱形ABCD外一点,连接AP、BP、CP,若∠CPB=120°,求证:CP+BP=AP；(3)如图3,M为菱形ABCD外一点,连接AM、CM、DM,若∠AMD=150°,
CM=2，DM=2，求四边形ACDM的面积。
16、（8分）解方程：
（1）；
（2）
17、（10分）在△ABC中，D是AC的中点，E是线段BC延长线一点，过点A作BE的平行线与线段ED的延长线交于点F，连接AE、CF．
（1）根据已知条件画出图形；
（2）求证：四边形AFCE是平行四边形．
18、（10分）黄岩岛是我国南沙群岛的一个小岛．一天某渔船离开港口前往该海域捕鱼．捕捞一段时间后，发现一艘外国舰艇进入我国水域向黄岩岛驶来，渔船向渔政部门报告，并立即返航．渔政船接到报告后，立即从该港口出发赶往黄岩岛．如图是渔政船及渔船与港口的距离s（海里）和渔船离开港口的时间t（时）之间的函数图象．（假设渔船与渔政船沿同一航线航行）
（1）直接写出渔船离开港口的距离s和渔船离开港口的时间t之间的函数关系式；
（2）已知两船相距不超过30海里时，可以用对讲机通话，在渔政船驶往黄岩岛的过程中，求两船可以用对讲机通话的时间长？
B卷（50分）
一、填空题（本大题共5个小题，每小题4分，共20分）
19、（4分）某书定价25元,如果一次购买20本以上,超过20本的部分打八折,试写出付款金额y(单位:元)与购书数量x(单位:本)之间的关系:______________.
20、（4分）已知一次函数的图像经过点，那么这个一次函数在轴上的截距为__________．
21、（4分）计算的结果是_____。
22、（4分）直线中，y随的减小而_______，图象经过______象限．
23、（4分）分式方程的解为_____．
二、解答题（本大题共3个小题，共30分）
24、（8分）甲、乙两车分别从A、B两地同时出发，甲车匀速前往B地，到达B地立即以另一速度按原路匀速返回到A地；乙车匀速前往A地，设甲、乙两车距A地的路程为y（千米），甲车行驶的时间为x（时），y与x之间的函数图象如图所示
（1）求甲车从A地到达B地的行驶时间；
（2）求甲车返回时y与x之间的函数关系式，并写出自变量x的取值范围；
（3）求乙车到达A地时甲车距A地的路程．
25、（10分）已知矩形0ABC在平面直角坐标系内的位置如图所示，点0为坐标原点，点A的坐标为(10，0)，点B的坐标为(10，8)，点Q为线段AC上-点，其坐标为(5，n).
(1)求直线AC的表达式
(2)如图，若点P为坐标轴上-动点，动点P沿折线AO→0C的路径以每秒1个单位长度的速度运动，到达C处停止求Δ0PQ的面积S与点P的运动时间t(秒)的函数关系式.
(3)若点P为坐标平面内任意-.点，是否存在这样的点P，使以0，C，P，Q为顶点的四边形为平行四边形?若存在，请直接写出点P的坐标，若不存在，请说明理由.
26、（12分）如图①，在△ABC中，∠ACB是直角，∠B=60°，AD、CE分别是∠BAC、∠BCA的平分线，AD、CE相交于点F．
（1）请你判断并写出FE与FD之间的数量关系（不需证明）；
（2）如图②，如果∠ACB不是直角，其他条件不变，那么在（1）中所得的结论是否仍然成立？若成立，请证明；若不成立，请说明理由．
参考答案与详细解析
一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、A
【解析】
由题意根据三角形具有稳定性解答．
【详解】
解：具有稳定性的图形是三角形．
故选：A．
本题考查三角形具有稳定性，是基础题，难度小，需熟记．
2、D
【解析】
根据矩形性质得出∠A=∠D=90°，AB=CD，AD∥BC，推出∠AEB=∠EBC，∠DEC=∠ECB，求出∠AEB=∠ABE，∠DCE=∠DEC，推出AB=AE，DE=DC，推出 AE=DE，根据SAS推出△ABE≌△DCE，推出BE=CE即可．
【详解】
∵四边形ABCD是矩形，
∴∠A=∠D=90°,AB=CD,AD∥BC，
∴∠AEB=∠EBC，∠DEC=∠ECB，
∵BE、CE分别平分∠ABC和∠DCB，
∴∠ABE=∠EBC，∠DCE=∠ECB，
∴∠AEB=∠ABE，∠DCE=∠DEC，
∴AB=AE，DE=DC，
∴AE=DE，
∴△ABE和△DCE都是等腰直角三角形，
在△ABE和△DCE中，
，
∴△ABE≌△DCE(SAS)，
∴BE=CE，∴①②③都正确，
故选D.
此题考查全等三角形的判定与性质，等腰直角三角形，等边三角形的判定，解题关键在于掌握各判定定理.
3、A
【解析】
由题意得，x≥0 .
故选A.
4、B
【解析】
解：根据函数的解析式可得：，=1，，则
故选：B．
本题考查反比例函数的性质，正确计算是解题关键．
5、C
【解析】
由平行四边形的性质和已知条件得出OD=4，CD+BC=12，再证明OE是△BCD的中位线，得出DE+OE=6，即可得出结果．
【详解】
解：∵四边形ABCD是平行四边形，
∴AB=CD，AD=BC，OB=OD=BD=4，
∵ABCD的周长为24，
∴CD+BC=12，
∵点E是CD的中点，
∴DE=CD，OE是△BCD的中位线，
∴OE=BC，
∴DE+OE=（CD+BC）=6，
∴△DOE的周长=OD+DE+OE=4+6=10；
故选C．
本题考查了平行四边形的性质、三角形中位线定理；熟练掌握平行四边形的性质，运用三角形中位线定理是解决问题的关键．
6、C
【解析】
因为,故选C.
7、C
【解析】
设每个A型包装箱可以装书x本，则每个B型包装箱可以装书（x+15）本，根据单独使用B型包装箱比单独使用A型包装箱可少用6个，列方程得：，故选C.
8、C
【解析】
根据勾股定理的逆定理，判断三角形是否为直角三角形，需要验证三角形三边关系，两小边长的平方和等于最长边的平方即可．
【详解】
A．，不能构成直角三角形，此选项错误；
B．，不能构成直角三角形，此选项错误；
C．，能构成直角三角形，此选项正确；
D．，不能构成直角三角形，此选项错误；
故选：C．
考查了勾股定理的逆定理，利用三角形三边关系判定三角形是否为直角三角形，用到实数平方的计算，熟记定理内容，注意判定时，边长是平方关系．
二、填空题（本大题共5个小题，每小题4分，共20分）
9、1．
【解析】
∵，
∴=0，b－2=0，解得a=3，b=2．
∵直角三角形的两直角边长为a、b，
∴该直角三角形的斜边长=．
10、1
【解析】
增根是分式方程化为整式方程后产生的使分式方程的分母为0的根．把增根代入化为整式方程的方程即可求出k的值．
【详解】
解：方程两边都乘（x-4），得
2x=k
∵原方程增根为x=4，
∴把x=4代入整式方程，得k=1，
故答案为：1．
此题考查分式方程的增根，解题关键在于掌握增根确定后可按如下步骤进行：化分式方程为整式方程；把增根代入整式方程即可求得相关字母的值．
11、a(a+3)(a-3)
【解析】
先提取公因式a，再用平方差公式分解即可.
【详解】
原式=a(a2-9)=a(a+3)(a-3).
故答案为a(a+3)(a-3).
本题考查了因式分解，把一个多项式化成几个整式的乘积的形式，叫做因式分解.因式分解常用的方法有：①提公因式法；②公式法；③十字相乘法；④分组分解法. 因式分解必须分解到每个因式都不能再分解为止.
12、y＝12－2x
【解析】
根据等腰三角形周长公式可求出底边长与腰的函数关系式，
【详解】
解：因为等腰三角形周长为12，根据等腰三角形周长公式可求出底边长y与腰x的函数关系式为：y=12-2x.
故答案为：y=12-2x.
本题考查一次函数的应用以及等腰三角形的周长及三边的关系，得出y与x的函数关系是解题关键．
13、
【解析】
先对原式进行化简，然后代入a,b的值计算即可．
【详解】
，
．
，
，
∴原式= ，
故答案为：．
本题主要考查二次根式的运算，掌握完全平方公式和平方差是解题的关键．
三、解答题（本大题共5个小题，共48分）
14、 (1)x1＝，x2＝﹣；(2)x1＝2，x2＝﹣2.
【解析】
(1)直接利用公式法求解即可；
(2)方程整理后，利用直接开平方法求解即可．
【详解】
解：(1)a＝6，b＝﹣1，c＝﹣2，
∵△＝1+48＝49，
∴x＝，
解得：x1＝，x2＝﹣；
(2)
方程整理得：x2＝12，
开方得：x＝±2，
解得：x1＝2，x2＝﹣2．
本题主要考查解一元二次方程，掌握解一元二次方程的方法，并能根据题目灵活选用合适的方法是解题的关键．
15、（1）∠BAC=60°；（2）见解析；（3）.
【解析】
（1）如图1中，证明△ABC是等边三角形即可解决问题．
（2）在PA上截取PH，使得PH=PC，连接CH．证明△PCB≌△HCA（SAS）即可；
（3）如图3中，作AH⊥DM交DM的延长线于H，延长AC到N，使得CN=AC，连接DN．证明A，N，D，M四点共圆，外接圆的圆心是点C，推出AD=CM= ，解直角三角形求出AH即可解决问题．
【详解】
解：（1）如图1中，
∵四边形ABCD是菱形，
∴AC⊥BD，∠ABD=∠CBD，
∴∠AOB=90°，
∵AB=2OA，
∴∠ABO=30°，
∴∠ABC=60°，
∵BA=BC，
∴△ABC是等边三角形，
∴∠BAC=60°；
（2）证明：如图2中，
在PA上截取PH，使得PH=PC，连接CH．
∵∠BPC=120°，∠BAC=60°，
∴∠BPC+∠BAC=180°，
∴A，B，P，C四点共圆，
∴∠APC=∠ABC=60°，
∵PH=PC，
∴△PCH是等边三角形，
∴PC=CH，∠PCH=∠ACB=60°，
∴∠PCB=∠HCA，
∵CB=CA，CP=CH，
∴△PCB≌△HCA（SAS），
∴PB=AH，
∴PA=PH+AH=PC+PB；
（3）解：如图3中，作AH⊥DM交DM的延长线于H，延长AC到N，使得CN=AC，连接DN．
∵CA=CD=CN，
∴∠ADN=90°，
∵CD=CN，
∴∠N=∠CDN，
∵∠ACD=60°=∠N+∠CDN，
∴∠N=30°，
∵∠AMD=150°，
∴∠N+∠AMD=180°，
∴A，N，D，M四点共圆，外接圆的圆心是点C，
∴CA=CD=AD=CM=，
在Rt△AHM中，∵∠AMH=30°，
∴MH=AH，设AH=x，则HM=x，
在Rt△ADH中，∵AD2=AH2+DH2，
∴28=x2+（x+2）2，
解得x=或-2（舍弃），
∴AH=，
∴S四边形ACDM=S△ACD+S△ADM=×+×2×=．
本题属于四边形综合题，考查了菱形的性质，等边三角形的判定和性质，解直角三角形，四点共圆，全等三角形的判定和性质等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题，属于中考压轴题．
16、（1）；（2）
【解析】
（1）两边开方，即可得出两个一元一次方程，求出方程的解即可；
（2）先把方程左边利用十字相乘法分解因式，即可得出两个一元一次方程，求出方程的解即可．
【详解】
解：（1）两边开方得：x-3=±3，
∴x-3=3或x-3=-3，
∴x1=6，x2=0；
（2）2x2+x-1=0，
∴（2x-1）（x+1）=0，
∴2x-1=0或x+1=0，
∴，x2=．
本题考查了解一元二次方程，能把一元二次方程转化成一元一次方程是解此题的关键．
17、（1）见解析；（2）见解析
【解析】
（1）根据已知条件画出图形即可；
（2）因为AF∥EC，得出∠DFA＝∠DEC，∠DAF＝∠DCE，因为D是AC的中点，可得DA＝DC，推出△DAF≌△DCE，得到AF＝CE，因为AF∥EC，即四边形AFCE是平行四边形；
【详解】
解：
（1）根据已知条件画出图形如下：

（2）证明：∵AF∥EC，
∴∠DFA＝∠DEC，∠DAF＝∠DCE，
∵D是AC的中点，
∴DA＝DC，
∴△DAF≌△DCE，
∴AF＝CE；
又∵AF∥EC，
∴四边形AFCE是平行四边形；
本题主要考查了平行四边形的判定与性质，掌握平行四边形的判定是解题的关键.
18、（1）答案见解析；（2）0.8小时．
【解析】
（1）由图象可得出渔船离港口的距离s和它离开港口的时间t的函数关系式，分为三段求函数关系式；
（2）在渔政船驶往黄岩岛的过程中，8＜t≤13，渔船与渔政船相距30海里，有两种可能：①s渔﹣s渔政=30，②s渔政﹣s渔=30，将函数关系式代入，列方程求t．
【详解】
解：（1）当0≤t≤5时，s＝30t，
当5＜t≤8时，s＝150，
当8＜t≤13时，s＝﹣30t+390；
（2）s渔＝﹣30t+390，s渔政＝45t﹣360，
分两种情况：
①s渔﹣s渔政＝30，﹣30t+390﹣（45t﹣360）＝30，解得t＝（或9.6）；
②s渔政﹣s渔＝30，45t﹣360﹣（﹣30t+390）＝30，解得t＝（或10.4）
所以10.4﹣9.6＝0.8（小时）
所以，两船可以用对讲机通话的时间长为0.8小时．
本题考查了一次函数的应用．关键是根据图象求出渔船的分段函数的解析式及渔政船行驶的函数关系式．
一、填空题（本大题共5个小题，每小题4分，共20分）
19、
【解析】
试题分析：本题采取分段收费，根据20本及以下单价为25元，20本以上，超过20本的部分打八折分别求出付款金额y与购书数x的函数关系式，再进行整理即可得出答案．
解：根据题意得：
y=，
整理得：；
则付款金额y（单位：元）与购书数量x（单位：本）之间的函数关系是y=；
故答案为y=．
考点：分段函数．
20、1
【解析】
先将代入中求出m的值，然后令求出y的值即可．
【详解】
∵一次函数的图像经过点，
∴，
解得，
∴．
令，则，
∴一次函数在轴上的截距为1．
故答案为：1．
本题主要考查待定系数法求一次函数的解析式，能够求出一次函数的解析式是解题的关键．
21、
【解析】
根据运算顺序，先对括号里进行通分，给a的分子分母都乘以a，然后利用分式的减法法则，分母不变，只把分子相减，进而除法法则，除以一个数等于乘以这个数的倒数，并把a2-1分解因式，约分即可得到化简结果．
【详解】
解：
故答案为：
此题考查学生灵活运用通分、约分的方法进行分式的加减及乘除运算，是一道基础题．注意运算的结果必须是最简分式．
22、减小 第一、三、四
【解析】
根据函数解析式和一次函数的性质可以解答本题．
【详解】
解：直线，，
随的减小而减小，函数图象经过第一、三、四象限，
故答案为：减小，第一、三、四．
本题考查一次函数的性质，解答本题的关键是明确题意，利用一次函数的性质解答．
23、x＝﹣3
【解析】
根据分式的方程的解法即可求出答案．
【详解】
解：，
∴，
∴（3﹣x）（1+x）＝x（1﹣x），
解得：x＝﹣3，
故答案为：x＝﹣3
本题考查分式方程，解题的关键是熟练运用分式的方程的解法，本题属于基础题型．
二、解答题（本大题共3个小题，共30分）
24、（1）2.5小时；（2）y=﹣100x+550；（3）175千米．
【解析】
试题分析：（1）根据题意列算式即可得到结论；
（2）根据题意列方程组即可得到结论；
（3）根据题意列算式即可得到结论．
试题解析：（1）300÷（180÷1.5）=2.5（小时）．
答：甲车从A地到达B地的行驶时间是2.5小时；
（2）设甲车返回时y与x之间的函数关系式为y=kx+b，∴，解得：，∴甲车返回时y与x之间的函数关系式是y=﹣100x+550（2.5≤x≤5.5）；
（3）300÷[（300﹣180）÷1.5]=3.75小时，当x=3.75时，y=175千米．
答：乙车到达A地时甲车距A地的路程是175千米．
考点：一次函数的应用；分段函数．
25、 (1) ； (2) 当点P在A0上运动时，S=2t+20 ，当点P在0C上运动时，S (10≤t≤18) ；(3)点P的坐标为(5，12)，(5，-4)，(-5，4)
【解析】
（1）由矩形的性质可得出点C的坐标，根据点A，C的坐标，利用待定系数法可求出直线AC的解析式；
（2）利用一次函数图象上点的坐标特征可求出点Q的坐标，分点P在OA和点P在OC上两种情况，利用三角形的面积公式可找出S与t之间的函数关系式；
（3）分OC为对角线、OQ为对角线以及CQ为对角线三种情况，利用平行四边形的性质（对角线互相平分）即可求出点P的坐标．
【详解】
解：(1)没直线AC的解析式为y=kx+b，
由题知C(0，8)，A(10，0)
∴
解之得
∴
(2)∵Q(5，n)在直线上
∴n=4
∴Q(5，4)
当点P在A0上运动时，
=2t+20
当点P在0C上运动时，
(10≤t≤18)
(3) 设点P的坐标为（a，c），分三种情况考虑（如图2）：
①当OC为对角线时，∵O（0，0），C（0，8），Q（5，4），
∴ ，解得： ，
∴点P1的坐标为（-5，4）；
②当OQ为对角线时，∵O（0，0），C（0，8），Q（5，4），
∴ ，解得： ，
∴点P2的坐标为（5，-4）；
③当CQ为对角线时，∵O（0，0），C（0，8），Q（5，4），
∴ ，解得： ，
∴点P3的坐标为（5，12）．
综上所述：存在点P，使以O，C，P，Q为顶点的四边形为平行四边形，点P的坐标为（-5，4），（5，-4），（5，12）．
故答案为：(1) ； (2) 当点P在A0上运动时，S=2t+20 ，当点P在0C上运动时，S (10≤t≤18) ；(3)点P的坐标为(5，12)，(5，-4)，(-5，4) ．
本题考查矩形的性质、待定系数法求一次函数解析式、一次函数图象上点的坐标特征、三角形的面积以及平行四边形的性质，解题的关键是：（1）根据点的坐标，利用待定系数法求出一次函数解析式；（2）分点P在OA和点P在OC上两种情况，找出S关于t的函数关系式；（3）分OC为对角线、OQ为对角线以及CQ为对角线三种情况，利用平行四边形的对角线互相平分求出点P的坐标．
26、（1）FE=FD （2）答案见解析
【解析】
（1）先在AC上截取AG=AE，连结FG，利用SAS判定△AEF≌△AGF，得出∠AFE=∠AFG，FE=FG，再利用ASA判定△CFG≌△CFD，得到FG=FD，进而得出FE=FD；
（2）先过点F分别作FG⊥AB于点G，FH⊥BC于点H，则∠FGE=∠FHD=90°，根据已知条件得到∠GEF=∠HDF，进而判定△EGF≌△DHF（AAS），即可得出FE=FD．也可以过点F作FG⊥AB于G，作FH⊥BC于H，作FK⊥AC于K，再判定△EFG≌△DFH（ASA），进而得出FE=FD．
【详解】
（1）FE与FD之间的数量关系为：FE=FD．
理由：如图，在AC上截取AG=AE，连结FG，
∵AD是∠BAC的平分线，
∴∠1=∠2，
在△AEF与△AGF中
，
∴△AEF≌△AGF（SAS），
∴∠AFE=∠AFG，FE=FG，
∵∠B=60°，AD，CE分别是∠BAC，∠BCA的平分线，
∴2∠2+2∠3+∠B=180°，
∴∠2+∠3=60°，
又∵∠AFE为△AFC的外角，
∴∠AFE=∠CFD=∠AFG=∠2+∠3=60°，
∴∠CFG=180°-60°-60°=60°，
∴∠GFC=∠DFC，
在△CFG与△CFD中，
，
∴△CFG≌△CFD（ASA），
∴FG=FD，
∴FE=FD；
（2）结论FE=FD仍然成立．
如图，过点F分别作FG⊥AB于点G，FH⊥BC于点H，则∠FGE=∠FHD=90°，

∵∠B=60°，且AD，CE分别是∠BAC，∠BCA的平分线，
∴∠2+∠3=60°，F是△ABC的内心，
∴∠GEF=∠BAC+∠3=∠1+∠2+∠3=60°+∠1，
∵F是△ABC的内心，即F在∠ABC的角平分线上，
∴FG=FH，
又∵∠HDF=∠B+∠1=60°+∠1，
∴∠GEF=∠HDF，
在△EGF与△DHF中，
，
∴△EGF≌△DHF（AAS），
∴FE=FD．
本题属于三角形综合题，主要考查了全等三角形的判定与性质，三角形外角性质，角平分线的性质以及三角形内角和定理的综合应用，解决问题的关键是作辅助线构造全等三角形，根据全等三角形的对应边相等进行推导．
题号
一
二
三
四
五
总分
得分
批阅人