初中数学鲁教版（五四学制）（2024）八年级上册1 图形的平移课前预习课件ppt

这是一份初中数学鲁教版（五四学制）（2024）八年级上册1 图形的平移课前预习课件ppt，共60页。
1.(跨学科·地理)(2024山西大同期末)下列关于天气的图案既 是轴对称图形又是中心对称图形的是 (　    )
A B C D
解析　A中的图案既是轴对称图形,又是中心对称图形.故选 A.
一、选择题(每小题3分,共30分)
2.(2023山东烟台莱州期末)我们学习了三种几何变换:平 移、轴对称、旋转,下列著名商标设计中,有三个都可以由基 本图形平移得到,则不能由基本图形通过平移变换得到的商 标是 (　    )
A B C D
解析　B、C、D中的图形可以由基本图形通过平移得到,A 中的图形无法由基本图形通过平移得到.故选A.
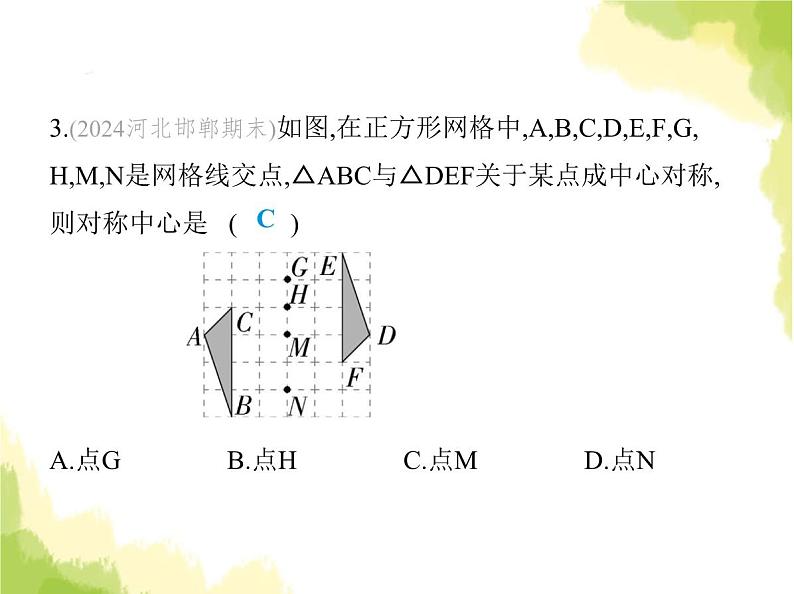
3.(2024河北邯郸期末)如图,在正方形网格中,A,B,C,D,E,F,G, H,M,N是网格线交点,△ABC与△DEF关于某点成中心对称, 则对称中心是 (　    ) A.点G　　　　B.点H　　　　C.点M　　　　D.点N
解析　连接AD、CF、BE相交于点M,∴△ABC与△DEF关 于点M成中心对称,故选C.
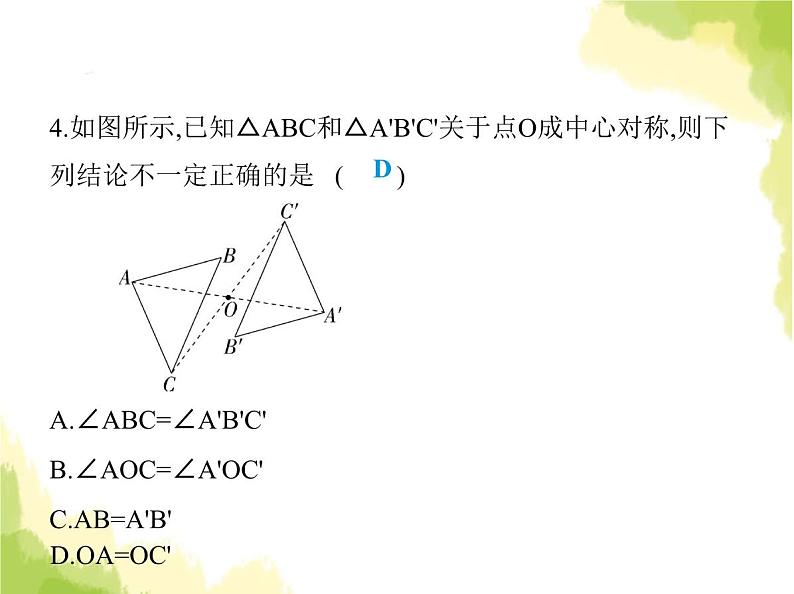
4.如图所示,已知△ABC和△A'B'C'关于点O成中心对称,则下 列结论不一定正确的是 (　    ) A.∠ABC=∠A'B'C'B.∠AOC=∠A'OC'C.AB=A'B'
解析　∵△ABC和△A'B'C'关于点O成中心对称,∴△ABC≌△A'B'C',∠AOC=∠A'OC',∴AB=A'B',∠ABC=∠A'B'C',故A,B,C选项结论正确;∵OA与OC'的大小关系无法确定,∴D选项结论不一定正确.故选D.
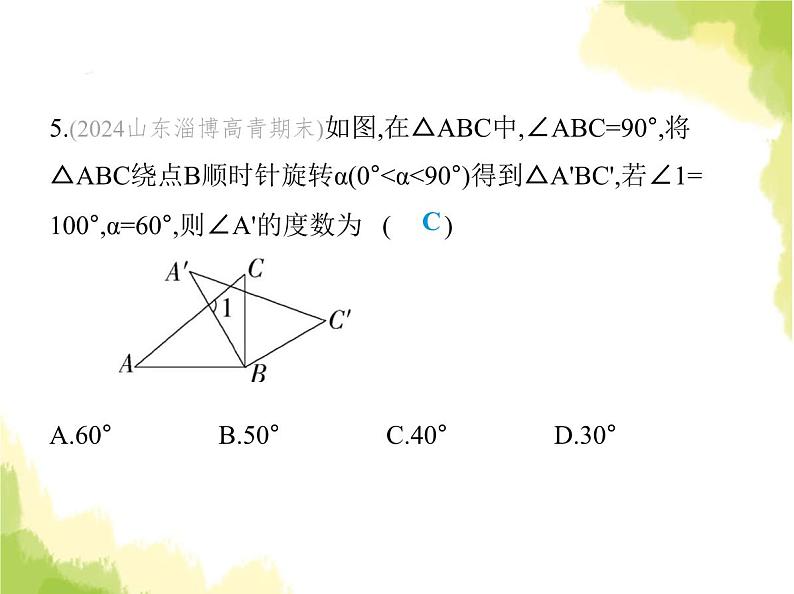
5.(2024山东淄博高青期末)如图,在△ABC中,∠ABC=90°,将 △ABC绕点B顺时针旋转α(0°180°,∴此种情况不成立;
④当ED=EA'时,如图3,  图3∴∠EDA'=∠A'=30°,∴∠DEA'=180°-∠EDA'-∠A'=120°,∵∠A'ED是△ACE的一个外角,
∴∠ACE=∠A'ED-∠A=90°,∴∠ACD=∠A'CD=α= ∠ACE=45°.综上所述,当△A'DE是等腰三角形时,∠α的度数为22.5°或6 7.5°或45°.故答案为22.5°或67.5°或45°.
易错警示    本题易出现分析不全面而漏解的情况.
三、解答题(共46分)
19.(8分)如图,在三角形ABC中,AC=4 cm,BC=3 cm,△ABC沿 AB方向平移至△DEF的位置,连接CF,若AE=8 cm,BD=2 cm.求:(1)平移的距离.(2)四边形AEFC的周长.
解析    (1)∵△ABC沿AB方向平移至△DEF的位置,∴AD= BE.∵AE=8 cm,DB=2 cm,∴AD=BE= =3 cm,故平移的距离是3 cm.(2)由平移的性质知,CF=AD=3 cm,EF=BC=3 cm,∵AE=8 cm,AC=4 cm,∴四边形AEFC的周长=AE+EF+CF+AC=8+3+3+4=18 cm.
故四边形AEFC的周长为18 cm.
20.(2024江西赣州信丰期末)(8分)如图,△ADE由△ABC绕点 A按逆时针方向旋转90°得到,且点B的对应点D恰好落在BC 的延长线上,AD,EC相交于点P.(1)求∠BDE的度数.(2)F是EC延长线上的点,且∠CDF=∠DAC.判断DF和PF的数 量关系,并证明.
解析    (1)由旋转的性质可知,AB=AD,∠BAD=90°,∠ADE= ∠B,∴∠B=∠ADB=45°,∴∠ADE=∠B=45°,∴∠BDE=∠ADB+∠ADE=90°.(2)DF=PF.证明如下:由旋转的性质可知,AC=AE,∠CAE=90°,∴∠ACE=∠AEC=45°,∵∠CDF=∠CAD,∠ACE=∠ADB=45°,∴∠ADB+∠CDF=∠ACE+∠CAD,即∠FPD=∠FDP,
21.(2023山东泰安泰山期末)(9分)如图,△ABC三个顶点分别 为A(1,1),B(4,2),C(3,4).(1)请画出△ABC向左平移4个单位长度后得到的图形△A1B1 C1,并写出A1,B1,C1的坐标.(2)请画出△ABC关于点(1,0)成中心对称的图形△A2B2C2.(3)若△A1B1C1绕点M旋转可以得到△A2B2C2,请直接写出点 M的坐标.
解析    (1)如图,△A1B1C1即为所求.A1(-3,1),B1(0,2),C1(-1,4).(2)如图,△A2B2C2即为所求.(3)点M如图所示,点M的坐标为(-1,0).
22.(手拉手模型)(10分)如图,△ABC、△ECD都是等边三角 形,且B、C、D在同一条直线上.(1)求证:BE=AD.(2)△EBC可以看成是△DAC经过平移、轴对称或旋转得到 的,请说明得到△EBC的过程.
解析    (1)证明:∵△ABC和△ECD都是等边三角形,∴AC=BC,EC=DC,∠ACB=∠ECD=60°,∴∠ACB+∠ACE=∠ECD+∠ACE,即∠ACD=∠BCE,在△ACD和△BCE中, ∴△ACD≌△BCE,∴AD=BE.
(2)∵△ECD是等边三角形,∴CD=CE,∠DCE=60°,∴以点C为旋转中心,将△DAC逆时针旋转60°能得到△EBC.
23.(2024山东淄博高青期末)(11分)阅读下面材料,并解决问 题:(1)如图1,等边△ABC内有一点P,若点P到顶点A、B、C的距 离分别为3,4,5,求∠APB的度数.为了解决本题,我们可以将△ABP绕顶点A旋转到△ACP'处, 此时△ACP'≌△ABP,这样就可以利用旋转变换将三条线段 PA、PB、PC转化到一个三角形中,从而求出∠APB=　        .基本运用:
请你利用第(1)问的方法,解答下面问题:(2)已知:如图2,△ABC中,∠CAB=90°,AB=AC,E、F为BC上 的点,且∠EAF=45°,求证:EF2=BE2+FC2.能力提升:(3)如图3,在Rt△ABC中,∠ACB=90°,AC=1,∠ABC=30°,点O 为Rt△ABC内一点,连接AO,BO,CO,且∠AOC=∠COB=∠BOA=120°,求OA+OB+OC的值.
图1 图2 图3
解析    (1)∵△ACP'≌△ABP,∴AP'=AP=3,CP'=BP=4,∠AP'C=∠APB,由题意知旋转角∠PAP'=60°,∴△APP'为等边三角形,∴PP'=AP=3,∠AP'P=60°,易证△PP'C为直角三角形,且∠PP'C=90°,∴∠APB=∠AP'C=∠AP'P+∠PP'C=60°+90°=150°.故答案为 150°.
(2)证明:如图,把△ABE绕点A逆时针旋转90°得到△ACE',连接E'F, 由旋转的性质知,AE'=AE,CE'=BE,∠CAE'=∠BAE,∠ACE'= ∠B,∠EAE'=90°,∵∠EAF=45°,∴∠E'AF=∠CAE'+∠CAF=∠BAE+∠CAF=∠BAC-∠EAF
=90°-45°=45°,∴∠EAF=∠E'AF,在△EAF和△E'AF中, ∴△EAF≌△E'AF(SAS),∴E'F=EF,∵∠CAB=90°,AB=AC,∴∠B=∠ACB=45°,
∴∠E'CF=45°+45°=90°,在Rt△E'CF中,由勾股定理得E'F2=CE'2+FC2,即EF2=BE2+FC2.(3)如图,将△AOB绕点B顺时针旋转60°至△A'O'B处,连接 OO',
∵在Rt△ABC中,∠ACB=90°,AC=1,∠ABC=30°,∴AB=2,∴BC= = ,∵△AOB绕点B顺时针旋转60°至△A'O'B处,∴∠A'BC=∠ABC+∠ABA'=30°+60°=90°,∵△AOB绕点B顺时针旋转60°,得到△A'O'B,∴A'B=AB=2,BO=BO',A'O'=AO,∠OBO'=60°,∠BO'A ' =∠AOB=120°,∴△BOO'是等边三角形,