2024-2025学年重庆一中八年级（上）入学数学试卷（含答案）

这是一份2024-2025学年重庆一中八年级（上）入学数学试卷（含答案），共15页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

1.下列各数中，是无理数的是( )
A. 75B. 3C. 0D. −3
2.第33届夏季奥运会将于2024年7月26日至8月11日在法国巴黎举行，下列巴黎奥运会的项目图标中，是轴对称图形的是( )
A. B. C. D.
3.下列运算正确的是( )
A. a6÷a4=aB. (2a2)3=4a6C. a2⋅a3=a6D. 4a2−a2=3a2
4.下列事件是必然事件的是( )
A. 黄河入海流B. 白发三千丈C. 鱼戏莲叶间D. 千山鸟飞绝
5.一个正方形的面积是27，估计这个正方形的边长在( )
A. 3到4之间B. 4到5之间C. 5到6之间D. 6到7之间
6.小南准备观察液体中的扩散现象，他先用水管匀速在空脸盆内注满水，然后将墨水滴在水面上，观察到墨水慢慢散开.为了验证墨水扩散速度与水的运动有关，小南在脸盆底部扎了一个口匀速放水.在整个过程中，能大致表示脸盆内水面高度与时间的关系图象是( )
A. B. C. D.
7.下列说法正确的是( )
A. 等腰三角形一边上的中线也是这条边上的高 B. 面积相等的两个三角形全等
C. 三角形三条角平分线的交点一定在三角形的内部 D. 两直线平行，内错角互补
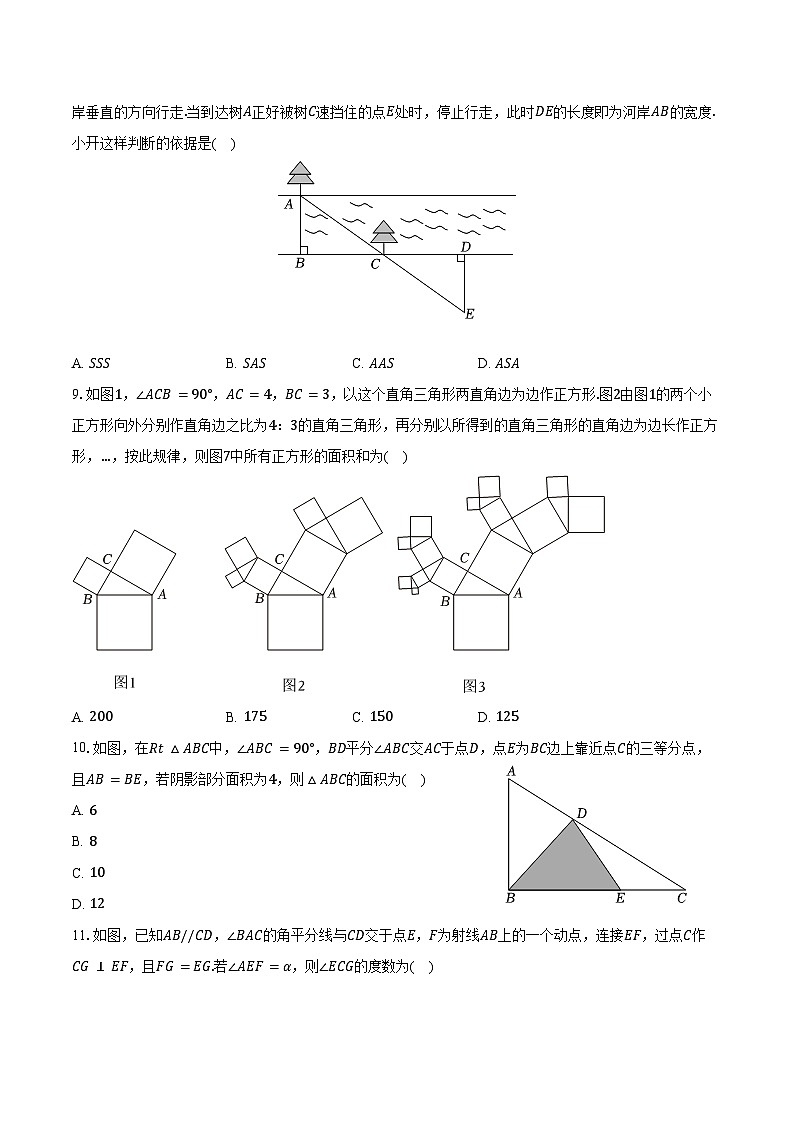
8.如图，某段河流的两岸是平行的，小开想出了一个不用涉水过河就能测得河的宽度的方案，首先在岸边点B处，选对岸正对的一棵树A，然后沿河岸直行20m到达树C，继续前行20m到达点D处，再从点D处沿河岸垂直的方向行走.当到达树A正好被树C速挡住的点E处时，停止行走，此时DE的长度即为河岸AB的宽度.小开这样判断的依据是( )
A. SSSB. SASC. AASD. ASA
9.如图1，∠ACB=90°，AC=4，BC=3，以这个直角三角形两直角边为边作正方形.图2由图1的两个小正方形向外分别作直角边之比为4：3的直角三角形，再分别以所得到的直角三角形的直角边为边长作正方形，…，按此规律，则图7中所有正方形的面积和为( )
A. 200B. 175C. 150D. 125
10.如图，在Rt△ABC中，∠ABC=90°，BD平分∠ABC交AC于点D，点E为BC边上靠近点C的三等分点，且AB=BE，若阴影部分面积为4，则△ABC的面积为( )
A. 6
B. 8
C. 10
D. 12
11.如图，已知AB//CD，∠BAC的角平分线与CD交于点E，F为射线AB上的一个动点，连接EF，过点C作CG⊥EF，且FG=EG.若∠AEF=α，则∠ECG的度数为( )
A. 45°−α2
B. 30°+α
C. 45°−α
D. 2α
12.在整式(3a2−1)，(−5a2+4a)，(8a2−4a+19)前添加“+”或“−”，先求和，再求和的绝对值的操作，称为“优绝对值”操作，将操作后的化简结果记为M.例如：|−(3a2−1)−(−5a2+4a)−(8a2−4a+19)|=|−6a2−18|=|6a2+18|=6a2+18，则M=6a2+18，当a=1时，M的化简求值结果为：M=6×12+18=24.下列说法正确的个数为( )
①至少存在一种“优绝对值”操作，使得操作后的化简结果为常数；
②把所有可能的“优绝对值”操作后的式子化简，共有8种不同的结果；
③在所有可能的“优绝对值”操作中，若操作后的化简求值的结果为17，则满足条件的a有且只有一个，此时a=−14．
A. 0B. 1C. 2D. 3
二、填空题：本题共8小题，每小题4分，共32分。
13.世界上最小的鱼是生活在澳大利亚东海岸的胖婴鱼，它的质量约为0.0000012千克，将数据0.0000012用科学记数法表示为______．
14.若代数式 x−1有意义，则x的取值范围为______．
15.已知△ABC两边长分别为4与5，第三边的长为奇数，则第三边的长的最大值为______．
16.若3− 2的整数部分为a，小数部分为b，则代数式(2+ 2a)⋅b的值是 ．
17.如图，将长方形ABCD沿AE折叠，点D恰好落在BC边的F点上，已知CF=4，AB=8，则AD= ______．
18.如图，在等边△ABC中，点D为线段AB上一点，BD=4AD，连接CD，点E为线段AC下方一点，连接CE，且CD=CE，∠BDC=∠ACE，连接BE交AC于点M，点F为线段AC延长线上一点，AD=CF，连接EF.已知AD=2，则CM的长为______．
19.如图，∠A=∠C=90°，且AB=AC=4，D，E分别为射线AC和射线CF上两动点，且AD=CE，当BD+BE有最小值时，则△BDE的面积为______．
20.对于任意一个三位自然数M，若它的各数位上的数字均不为0，且满足十位数字与百位数字之差等于个位数字与十位数字之差的2倍，则称M为“2阶等差中项数”，将这个三位自然数M的百位数字和个位数字互换位置，得到M′，规定F(M)=M−M′99.已知A、B均为“2阶等差中项数”，其中A=310+10x+y，B=100m+70+n(1≤x≤8,1≤y,m,n≤9，且x，y，m，n均为正整数).令k=F(A)F(B)，当30−3F(A)−F(B)为完全平方数时，则满足条件的所有k之和为______．
三、解答题：本题共8小题，共82分。解答应写出文字说明，证明过程或演算步骤。
21.(本小题10分)
在等腰Rt△ABC中，∠ACB=90°，AC=BC，点D是BC上的任意一点，连接AD，过点C作CE⊥AD交AD于点E．
(l)如图1，若∠BAD=15°，CE= 3，CD=2，求△ACD的面积；
(2)如图2，过C作CF⊥BF，且CF=CE，连接FE并延长FE交AB于M，连接BF，求证：AM=BM．
22.(本小题16分)
计算：
(1)(−1)2024+(−13)−2−( 3+1)0；
(2)(2a2)3⋅3a−7a6⋅a3÷a2+2a7；
(3)(2m−5n)2−(2m+5n)2；
(4)(1+ 2)2+ 45− 24÷ 3．
23.(本小题6分)
先化简，再求值：[(4a−3b)(a+3b)−(a−2b)(a+2b)+5b2]÷3a，其中a=4，b=−23．
24.(本小题8分)
如图，已知在△ABC中，∠BAC=90°，AD⊥BC于点D．

(1)尺规作图：作∠ABC的平分线交AC于点E，交AD于点F；(要求：保留作图痕迹，不写作法，不下结论)
(2)在(1)的条件下，求证：∠AFE=AEF．
∵AD⊥BC，
∴∠ADB=90°，
∴ ______+∠BFD=90°，
又∵∠BFD= ______，
∴∠FBD+ ______=90°，
∵∠BAC=90°，
∴∠ABF+ ______=90°，
∵BF平分∠ABC，
∴∠ABF= ______，
∴∠AFE=AEF．
25.(本小题10分)
“五月五是端阳，插艾叶戴香囊，吃粽子撒白糖，龙船下水喜洋洋.”端午是我国传统节日，也是集拜神祭祖，祈福辟邪，欢庆娱乐和饮食为一体的民俗大节.某校为了更好地调动学生参与端午活动的积极性，采取抽样调查的方法，调查了学生感兴趣的四项端午习俗项目：插艾叶，戴香囊，吃粽子，赛龙舟，并将调查结果绘制成下面两幅不完整的统计图，请你根据图中提供的信息解答下列问题：

(1)在这次调查中，一共调查了______名学生，扇形统计图中m的值为______；
(2)补全条形统计图；
(3)若该校共有3000名学生，请估计该校对插艾叶项目感兴趣的学生有多少人？
26.(本小题10分)
某花店分别以22元/盆和30元/盆的价格两次购进甲、乙两种绿植.花店第一次购进两种绿植共花费4600元，其中甲种绿植盆数的2倍比乙种绿植盆数的3倍少40盆．
(1)请计算该花店第一次分别购进甲、乙两种绿植各多少盆．
(2)该花店将第一次购进的甲、乙两种绿植分别以28元/盆和40元/盆的价格全部售出，则卖出后一共可获得利润______元.
(3)该花店第二次购买这两种绿植时进价不变，其中甲种绿植盆数是第一次的2倍，乙种绿植盆数不变.甲种绿植仍按原售价销售，乙种绿植打折销售.第二次甲、乙两种绿植销售完以后获得的利润比第一次获得的利润多280元，则第二次乙种绿植是按原售价打几折销售的？
27.(本小题10分)
如图1，已知八边形ABCDEFGH相邻的两边互相垂直，且AB=AH，DC=DE.动点P从八边形顶点A出发，沿着八边形的边以每秒a cm的速度逆时针运动，当P运动到点E时调头，以原来的速度原路返回，到A点处停止运动.△PAH的面积为S(cm2)，运动时间为t(秒)，S与t的图象如图2所示，请回答以下问题：
(1)AB= ______cm，DE= ______cm，a= ______cm/s；
(2)当点P第一次在边CD上运动时，求S与t的关系式；
(3)点P在返回过程中，当时间t为何值时，△AHP为等腰三角形？请直接写出t的值．
28.(本小题12分)
已知△ABC中，AB=AC，∠BAC=120°，E为AC边上的中点，取平面上一点D，连接CD，使得∠ACD=∠BAC.连接AD交BE于点F，∠AFB=60°．
(1)如图1，求证：CD=CE；
(2)如图2，延长BE至点G，使得EG=FD，连接CG，CF，求证：BF=3AF；
(3)如图3，若P为直线BE上一点，连接AP，在AP左侧作等边△APQ，连接BQ，若AB=4，请直接写出BQ的最小值．
参考答案
1.B 2.C 3.D 4.A 5.C 6.A 7.C 8.D 9.A 10.C
11.A 12.B
13.1.2×10−6
14.x≥1
15.7
16.2
17.10
18.4
19.6
20.−1
21.(1)解：∵∠ACB=90°，AC=BC，
∴∠BAC=∠B=45°，
∵∠BAD=45°
∴∠CAD=45°−15°=30°，
在Rt△ACD中，CD=2，
∴AD=2CD=4，
∵CE⊥AD，CE= 3
∴S△ACD=12AD×CE=2 3；
(2)证明：过点A作AG//BF交FM的延长线于点G，
在Rt△ECF中，∠ECF=90°，EC=FC，
∵∠ACB=∠ECF=90°，
∴∠ACB−∠ECB=∠ECF−∠ECB，即∠ECA=∠FCB
又∵AC=BC，CE=CF，
∴△ACE≌△BCF(SAS)，
∴AE=BF，
在Rt△ECF中，∠ECF=90°，EC=FC，
∴∠CEF=∠CFE=45°，
∴∠AEG=180°−90°−45°=45°，∠BFE=90°−45°=45°，
∴∠AEG=∠BFE，
∵AG//BF，
∴∠G=∠BFE，∠GAM=∠FBM，
∴∠AEG=∠G，
∴AE=AG
∵AE=BF，
∴BF=AG，
在△AMG和△BMF中，
∠G=∠BFE∠GAM=∠FBMBF=AG，
∴△AMG≌△BMF(ASA)，
∴AM=BM．
22.解：(1)(−1)2024+(−13)−2−( 3+1)0
=1+9−1
=9；
(2)(2a2)3⋅3a−7a6⋅a3÷a2+2a7；
=8a6⋅3a−7a6⋅a3÷a2+2a7
=24a7−7a7+2a7
=19a7；
(3)(2m−5n)2−(2m+5n)2；
=4m2−20mn+25n2−4m2−20mn−25n2
=−40mn；
(4)(1+ 2)2+ 45− 24÷ 3
=3+2 2+3 5−2 6÷ 3
=3+2 2+3 5−2 2
=3+3 5．
23.解：[(4a−3b)(a+3b)−(a−2b)(a+2b)+5b2]÷3a
=[4a2+9ab−9b2−(a2−4b2)+5b2]÷3a
=(4a2+9ab−9b2−a2+4b2+5b2)÷3a
=(3a2+9ab)÷3a
=a+3b，
当a=4，b=−23时，原式=4+3×(−23)=4−2=2．
24.

25.（1）100 10
26.

27.（1）10 5 2
28.(1)证明：∵∠ACD=∠BAC=120°，
∴∠DAC+∠D=60°，
∵∠AFB=60°，
∴∠DAC+∠AEB=60°，
∴∠AEB=∠D，
∵AB=AC，
∴△ABE≌△CAD(AAS)，
∴CD=AE，
∵点E是AC的中点，
∴AE=CE，
∴CD=CE；
(2)方法一，如图1，

作AH⊥AF，交BG于H，
∴∠HAF=90°，
∵∠AFB=60°，
∴∠AHF=30°，
∴HF=2AF，
由(1)知，
CE=CD，∠AEB=∠D，∠ABE=∠CAD，
∵∠CEG=∠AEB，
∴∠D=∠CEG，
∵EG=DF，
∴△CDF≌△CEG(SAS)，
∴∠G=∠DFC，CG=CF，
∴∠G=∠CFG，
∴∠CFG=∠DFC，
∵∠DFG=∠AFB=60°，
∴∠DFC=∠CFG=30°，
∴∠AHF=∠DFC，
∴∠AHB=∠AFC，
∵AB=AC，
∴△ABH≌△CAF(AAS)，
∴BH=AF，
∴BF=3AF，
方法二，如图2，

在FD上截取FW=AF，在FB上截取FV=AF，连接CW，AV，
∴AW=2AF，
∵E是AC的中点，
∴EF//CW，
∴∠AWC=∠AFE=180°−∠AFB=120°，
∵∠AFB=60°，
∴△AFV是等边三角形，
∴AV=AF，∠AVF=60°，
∴∠AVB=120°，
∴∠AWC=∠AVB，
∵∠ABF=∠DAC，AB=AC，
∴△ABV≌△CAW(AAS)，
∴BV=AW=2AF，
∴BF=3AF；
(3)解：如图3，

在BF上截取FV=AF，连接AV，连接QV，作BQ′⊥QV于Q′，作AR⊥BE于R，
由(2)知，
△AFV是等边三角形，
∴∠FAV=∠AVF=60°，AF=AV，VR=FR，
∵△APQ是等边三角形，
∴∠PAQ=60°，AP=AQ，
∴∠PAQ=∠FAV，
∴∠PAQ+∠PAV=∠FAV+∠PAV，
∴∠PAF=∠QAV，
∴△PAF≌△QAV(SAS)，
∴∠AVQ=∠AFB=60°，
∴∠BVQ=180°−∠AVQ−∠AVF=60°，
∴点Q在过点V，与BV夹角是60° 的直线上运动，
∴当点Q在Q′处时，BQ最小，
设AF=2x，则BV=2AF=4x，
∵∠AFB=60°，
∴VR=FR=12AF=x，AR= 32AF= 3x，
在Rt△ABR中，AR= 3x，AB=4，BR=BV+VR=5x，
∴(5x)2+( 3x)2=42，
∴x=2 77，
∴BV=4x=8 77，
∵∠BVQ′=60°，
∴BQ′= 32BV=4 217，
∴BQ的最小值为：4 217．