

四川省成都市树德中学2024-2025学年高三上学期开学考试数学试题
展开1.“”的否定是( )
A.,使得 B.
C.,使得 D.
2.已知全集,集合,则图中阴影部分表示的集合的子集个数为( )
A.2 B.4 C.8 D.16
3.已知等差数列的公差为,前项和为,则“”是“是递增数列”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
4.在同一平面直角坐标系中,直线与圆的位置不可能为( )
A.B.
C.D.
5.一堆苹果中大果与小果的比例为,现用一台水果分选机进行筛选.已知这台分选机把大果筛选为小果的概率为,把小果筛选为大果的概率为.经过一轮筛选后,现在从这台分选机筛选出来的“大果”里面随机抽取一个,则这个“大果”是真的大果的概率为( )
A. B. C. D.
6.某省高考改革试点方案规定:2023年高考总成绩由语文、数学、外语三门统考科目和思想政治、历史、地理、物理、化学、生物六门选考科目组成,将每门选考科目的考生原始成绩从高到低划分为,共8个等级,参照正态分布原则,确定各等级人数所占比例分别为,,选考科目成绩计入考生总成绩时,将至等级内的考生原始成绩,依照等比例转换法则,分别转换到八个分数区间,得到考生的等级成绩,如果该省某次高考模拟考试物理科目的原始成绩,那么等级的原始分最低大约为( )
参考数据:对任何一个正态分布来说,通过转化为标准正态分布,从而查标准正态分布表得到.可供查阅的(部分)标准正态分布表:
A.57 B.64 C.71 D.77
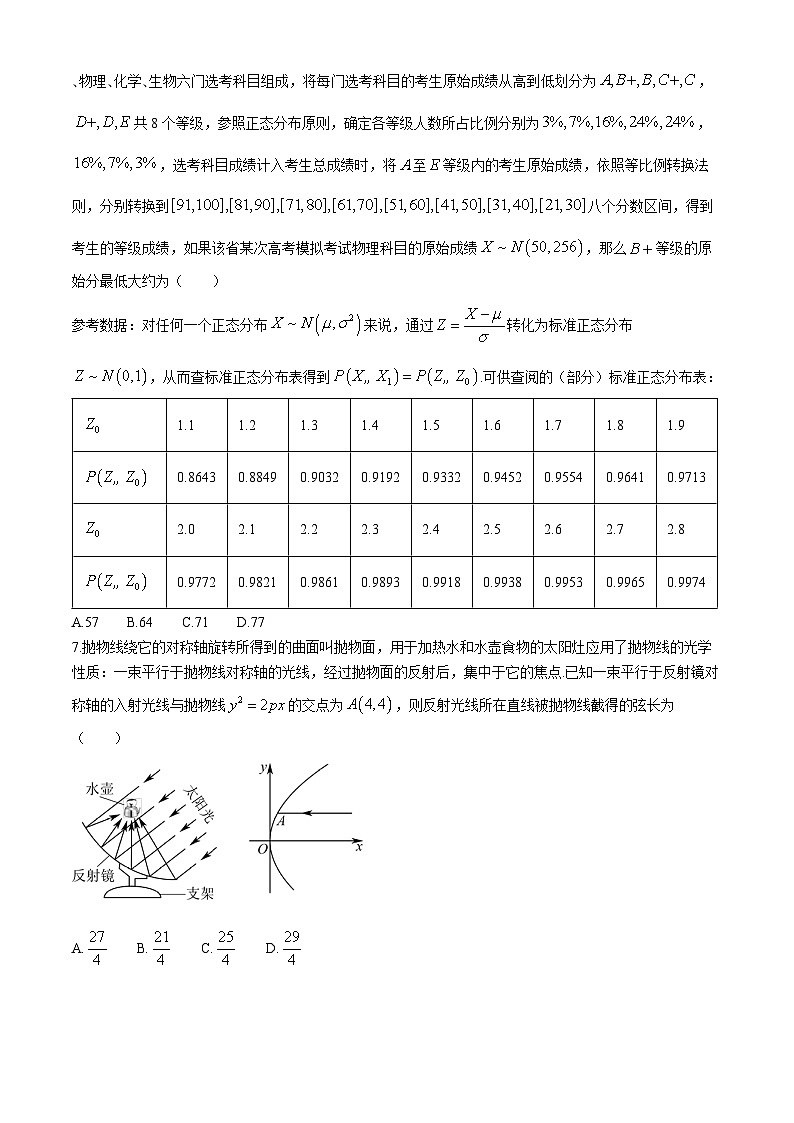
7.抛物线绕它的对称轴旋转所得到的曲面叫抛物面,用于加热水和水壶食物的太阳灶应用了抛物线的光学性质:一束平行于抛物线对称轴的光线,经过抛物面的反射后,集中于它的焦点.已知一束平行于反射镜对称轴的入射光线与抛物线的交点为,则反射光线所在直线被抛物线截得的弦长为( )
A. B. C. D.
8.若对任意的恒成立,则的最小值为( )
A. B. C. D.
二、多项选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全选对的得6分,部分选对的得部分分,有选错的得0分.
9.某科技企业为了对一种新研制的专利产品进行合理定价,将该产品按事先拟定的价格进行试销,得到如下数据:
由表中数据,求得线性回归方程为,则下列说法正确的是( )
A.产品的销量与单价成负相关
B.为了获得最大的销售额(销售额单价销量),单价应定为70元或80元
C.
D.若在这些样本点中任取一点,则它在线性回归直线左下方的概率为
10.已知,则下列结论正确的是( )
A.若,则
B.若,则
C.若
D.的最小值为
11.伯努利双纽线最早于1694年被瑞士数学家雅各布•伯努利用来描述他所发现的曲线.在平面直角坐标系中,把到定点距离之积等于的点的轨迹称为双纽线,已知点是的双纽线上一点,下列说法正确的是( )
A.若直线交双纽线于三点(为坐标原点),则
B.双纽线上满足的点有2个
C.的面积的最大值为
D.的周长的取值范围为
三、填空题:本大题共3小题,每小题5分,共计15分.
12.若,则__________;__________.
13.若不等式成立的一个充分不必要条件是,则实数的取值范围为__________.
14.设函数,正实数满足,若,则实数的最大值为__________.
四、解答题:共77分.解答应写出文字说明,证明过程或演算步骤.
15.已知函数.
(1)若,求不等式的解集;
(2)若,对,使得成立,求的取值范围.
16.2021届高考体检工作即将开展,为了了解高三学生的视力情况,某校医务室提前对本校的高三学生视力情况进行调查,在高三年级1000名学生中随机抽取了100名学生的体检数据,并得到如下图的频率分布直方图.
(1)若直方图中前四组的频数依次成等比数列,试估计全年级高三学生视力的中位数(精确到0.01);
(2)该校医务室发现,学习成绩突出的学生,近视的比较多,为了研究学生的视力与学习成绩是否有关系,对抽取的100名学生名次在1~100名和101~1000名的学生的体检数据进行了统计,得到表中数据,根据表中的数据,能否在犯错的概率不超过0.05的前提下认为视力与学习成绩有关系?
(3)在(2)中调查的不近视的学生中按照分层抽样抽取了6人,进一步调查他们良好的护眼习惯,求在这6人中任取2人,至少有1人的年级名次在名的概率.
,其中.
17.在三棱台中,平面,且为的中点,是上一点,且.
(1)求证:平面;
(2)已知,且直线与平面的所成角的正弦值为时,求平面与平面所成夹角的余弦值.
18.如图,双曲线的左、右焦点分别为双曲线的左、右顶点,过点的直线分别交双曲线的左、右两支于两点,交双曲线的右支于点(与点不重合),且与的周长之差为2.
(1)求双曲线的方程;
(2)若直线交双曲线的右支于两点.
①记直线的斜率为,直线的斜率为,求的值;
②试探究:是否为定值?并说明理由.
19.设实系数一元二次方程①,有两根,则方程可变形为,展开得②,比较①②可以得到这表明,任何一个一元二次方程的根与系数的关系为:两个根的和等于一次项系数与二次项系数的比的相反数,两个根的积等于常数项与二次项系数的比.这就是我们熟知的一元二次方程的韦达定理.事实上,与二次方程类似,一元三次方程也有韦达定理.
设方程有三个根,则有③
(1)证明公式③,即一元三次方程的韦达定理;
(2)已知函数恰有两个零点.
(i)求证:的其中一个零点大于0,另一个零点大于且小于0;
(ii)求的取值范围.
树德中学高2022级高三开学数学考试试题
参考答案
1.A 2.B 3.B 4.C 5.A 6.C 7.C 8.D
9.ACD 10.BC 11.ACD
8.【详解】因为,所以,则可化为,
整理得,因为,所以,
令,则函数在上单调递减,
则在上恒成立,所以在上恒成立,
令,则在上恒成立,
则在上单调递减,所以,
故,所以得最小值为.
11.【详解】由双纽线的定义可得:,
即,化简得:,
当时,点的轨迹方程为,
令,解得或,所以,故A正确;
因为,若满足,则点在轴上,
在方程中令,解得,
所以满足的点为,只有一个,故B错误;
,故C正确;
因为,
又,且,所以,
接下来先证明
在中,由余弦定理可得,
所以.
又因为,所以
所以
,即,
整理可得,所以;所以,
如图以为邻边作平行四边形,
则,所以,
所以,
即的周长的取值范围为,故D正确.
12., 13. 14.
14.【详解】因为,所以,
又,所以,即,
因为,所以,所以,所以,
又,即,所以,所以,
令,则,所以
,
当且仅当,即时取等号,
所以,所以,则实数的最大值为.
15.(1)时,不等式的解集为;
时,不等式的解集为;
时,不等式的解集为;
(2);
16.【详解】(1)由图可知,第三组和第六组的频数为人
第五组的频数为人
所以前四组的频数和为人
而前四组的频数依次成等比数列
故第一组的频数为4人,第二组的频数为8人,第四组的频数为32人
所以中位数落在第四组,设为,
因此有或
解得所以中位数是4.74
(2)因为,所以
因此在犯错的概率不超过0.05的前提下认为视力与学习成绩有关系
(3)依题意按照分层抽样在不近视的学生中抽取了6人中年级名次在1~100名和101~1000名的分别有2人和4人,从6人中任意抽取2人的基本事件共15个至少有1人来自于名的基本事件有9个,所以至少有1人的年级名次在名的概率为.
17.(1),且是的中点,则.
平面平面.
又平面平面,
因为平面.①
,则.
在平面中.②
平面由①②知平面.
(2)由题意得平面,
平面.由(1)可知,故为坐标原点.
如图,以所在直线分别为轴,建立空间直角坐标系.
.
,
由棱台的性质得.
由(1)可知平面的一个法向量为,且.
直线与平面的所成角的正弦值为,
,
即,解得.
平面的一个法向量为,且.
平面的法向量为.
,
,即,当时,.
平面的一个法向量为
平面与平面所成夹角的余弦值.
18.(1)解:设,因为与的周长之差为2,
所以,即,
又因为分别为双曲线的左、右顶点,所以,
联立方程组,解得,所以,
故双曲线的方程为.
(2)解:①由(1)知,双曲线的方程为,
设,则,可得,
则.
②为定值4.
理由如下:
由(1)得直线的方程为,
联立方程组,整理得,
设,则,
因为位于双曲线的左、右两支,所以,即,
可得,
又因为,所以直线的方程为,
根据双曲线的对称性,同理可得,
所以,故为定值4.
19.(1)证明:因为方程有三个根,
所以方程即为,
变形为,
比较两个方程可得.
(2)(i)证明:有两个零点,
有一个二重根,一个一重根,且
由(1)可得,由可得.
由可得.
联立上两式可得,解得,
又,综上.
(ii)解:由(i)可得,
令,则,
,当时,,
在上单调递增,,
.1.1
1.2
1.3
1.4
1.5
1.6
1.7
1.8
1.9
0.8643
0.8849
0.9032
0.9192
0.9332
0.9452
0.9554
0.9641
0.9713
2.0
2.1
2.2
2.3
2.4
2.5
2.6
2.7
2.8
0.9772
0.9821
0.9861
0.9893
0.9918
0.9938
0.9953
0.9965
0.9974
单价元
40
50
60
70
80
90
销量件
50
44
43
35
28
年级名次
是否近视
近视
40
30
不近视
10
20
0.10
0.05
0.025
0.010
0.005
2.706
3.841
5.024
6.635
7.879
四川省成都市树德中学2024-2025学年高三上学期开学考试数学试卷(PDF版附答案): 这是一份四川省成都市树德中学2024-2025学年高三上学期开学考试数学试卷(PDF版附答案),文件包含开学考试答案-数学pdf、树德中学高2022级高三开学数学pdf等2份试卷配套教学资源,其中试卷共8页, 欢迎下载使用。
四川省成都市石室中学2024-2025学年高三上学期开学考试数学试题(Word版附答案): 这是一份四川省成都市石室中学2024-2025学年高三上学期开学考试数学试题(Word版附答案),共10页。试卷主要包含了635等内容,欢迎下载使用。
_数学文|四川省成都市树德中学2024届高三上学期开学考试数学文试卷及答案: 这是一份_数学文|四川省成都市树德中学2024届高三上学期开学考试数学文试卷及答案,共8页。












