

2025年高考数学精品教案第十章 计数原理 概率 随机变量及其分布 第3讲 二项式定理
展开学生用书P229
1.二项式定理
辨析比较
二项式系数与项的系数的区别
(a+bx)n的二项展开式中,二项式系数是指Cn0,Cn1,…,Cnn,其与a,b的值无关,如第k+1项的二项式系数是Cnk;而项的系数是指该项中除变量外的常数部分,其与a,b的值有关,如第k+1项的系数是Cnkan-kbk.
2.二项式系数的性质
1.[北京高考]在(x-2)5的展开式中,x2的系数为( C )
A.-5B.5C.-10D.10
解析 由二项式定理得(x-2)5的展开式的通项Tr+1=C5r(x)5-r(-2)r=C5r-2rx5-r2,令5-r2=2,得r=1,所以T2=C51(-2)x2=-10x2,所以x2的系数-10,故选C.
2.[教材改编]在(x-y)10的展开式中,系数最小的项是( C )
A.第4项B.第5项C.第6项D.第7项
解析 展开式共有11项,奇数项系数为正,偶数项系数为负,且第6项的二项式系数最大,则展开式中系数最小的项是第6项.
3.已知Cn0+2Cn1+22Cn3+23Cn3+…+2nCnn=243,则Cn1+Cn2+Cn3+…+Cnn=( A )
A.31B.32C.15D.16
解析 逆用二项式定理得Cn0+2Cn1+22Cn2+23Cn3+…+2nCnn=(1+2)n=243,即3n=35,所以n=5,所以Cn1+Cn2+Cn3+…+Cnn=25-1=31.
4.[多选]下列说法正确的是( CD )
A.Cnkan-kbk是(a+b)n展开式中的第k项
B.在二项展开式中,系数最大的项为中间的一项或中间的两项
C.在(a+b)n的展开式中,每一项的二项式系数都与a,b无关
D.在(a+b)n的展开式中,某项的系数与该项的二项式系数不同
5.[易错题]已知(2x-1)n=a0+a1x+a2x2+…+anxn(n∈N*),设(2x-1)n的展开式中所有项的二项式系数和为Sn,Tn=a1+a2+…+an(n∈N*),则 S4= 16 ,T4= 0 .
解析 因为(2x-1)n展开式中所有项的二项式系数和为2n,(易混淆:(2x-1)n展开式的二项式系数和为Cn0+Cn1+Cn2+…+Cnn=2n,系数和为a0+a1+a2+…+an)
所以Sn=2n,S4=16.令x=0,则(-1)n=a0,令x=1,则1=a0+a1+a2+…+an,所以Tn=1-(-1)n,所以T4=0.
学生用书P230
命题点1 展开式中的特定项问题
角度1 形如(a+b)n(n∈N*)的展开式中的特定项
例1 (1)[2023南京市中华中学检测]若2-x6=a0+a11+x+a21+x2+…+a61+x6,则a4=( B )
A.270B.135
C.-135D.-270
解析 (2-x)6=a0+a1(1+x)+a2(1+x)2+…+a6(1+x)6,以x-1代替x,得(3-x)6=a0+a1x+a2x2+…+a6x6,而(3-x)6的展开式的通项公式为Tr+1=C6r36-r-xr=C6r36-r(-1)rxr,令r=4,则a4=C64×36-4×(-1)4=135,故选B.
(2)[2023天津高考]在(2x3-1x)6的展开式中,x2的系数是 60 .
解析 解法一 二项式(2x3-1x)6的展开式的通项Tk+1=C6k(2x3)6-k(-1x)k=-1k26-kC6kx18-4k,令18-4k=2,解得k=4,所以x2的系数为(-1)4×22×C64=60.
解法二 将二项式(2x3-1x)6看成6个多项式(2x3-1x)相乘,要想出现x2项,则先在6个多项式中选2个多项式取2x3,然后余下的多项式都取-1x,相乘,即C622x32×C44-1x4=60x2,所以x2的系数为60.
方法技巧
求形如(a+b)n(n∈N*)的展开式中的特定项问题的步骤
角度2 形如(a+b)m(c+d)n(m,n∈N*)的展开式中的特定项
例2 (1)[2023沈阳市三检](2x-3)2(1-1x)6的展开式中,含x-2项的系数为( B )
A.430B.435C.245D.240
解析 (1-1x)6的展开式的通项Tk+1=C6k(-1x)k=(-1)kC6k1xk.(2x-3)2=4x2-12x+9,当在多项式(4x2-12x+9)中取4x2时,令k=4,得4x2·(-1)4C641x4;当在多项式(4x2-12x+9)中取-12x时,令k=3,得-12x·(-1)3C631x3;当在多项式(4x2-12x+9)中取9时,令k=2,得9×(-1)2C621x2.所以含x-2项的系数为4×(-1)4C64+(-12)×(-1)3C63+9×(-1)2C62=60+240+135=435,故选B.
(2)[2022新高考卷Ⅰ](1-yx)(x+y)8的展开式中x2y6的系数为 -28 .(用数字作答)
解析 (x+y)8的展开式的通项Tr+1=C8rx8-ryr,r=0,1,…,7,8.令r=6,得T6+1=C86x2y6,令r=5,得T5+1=C85x3y5,所以(1-yx)(x+y)8的展开式中x2y6的系数为C86-C85=-28.
方法技巧
求形如(a+b)m(c+d)n(m,n∈N*)的展开式中特定项问题的步骤
角度3 形如(a+b+c)n(n∈N*)的展开式中的特定项
例3 (1)(x-y+2)5的展开式中,x3y的系数为( D )
A.80B.40
C.-80D.-40
解析 解法一 (x-y+2)5=[x-(y-2)]5,其通项Tr+1=C5rx5-r(-1)r·(y-2)r,则展开式中含x3的项为C52x3(y-2)2,又(y-2)2的展开式中含y的项为(-2)C21y,所以(x-y+2)5的展开式中,x3y的系数为C52·C21·(-2)=-40,故选D.
解法二 要在展开式中得到x3y,可在5个“x-y+2”中选3个“x”,1个“-y”,1个“2”,故x3y的系数为C53·C21(-1)1×2=-40.
(2)(1+2x-3x2)5的展开式中,x5的系数为 92 .
解析 (1+2x-3x2)5=(1-x)5(1+3x)5,所以展开式中x5的系数为C50C5535+C51(-1)C5434+C52(-1)2C5333+C53(-1)3C5232+C54(-1)4C5131+C55(-1)5C5030=92.
方法技巧
求形如(a+b+c)n(n∈N*)的展开式中的特定项问题的方法
训练1 (1)已知(2x-a)(x+2x)6的展开式中x2的系数为-240,则该展开式中的常数项为( A )
A.-640B.-320C.640D.320
解析 (x+2x)6的展开式的通项为Tk+1=C6kx6-k·(2x)k=C6k2kx6-2k.令6-2k=2,得k=2;令6-2k=1,得k=52,舍去.(注意:k取整数)
故(2x-a)(x+2x)6的展开式中x2的系数为-aC62·22=-240,得a=4.
令6-2k=-1,得k=72,不符合题意,舍去;令6-2k=0,得k=3.故2x-4x+2x6的展开式中的常数项为-4×C63×23=-640.
(2)(x2+x+y)5的展开式中,x5y2的系数为( C )
A.10B.20C.30D.60
解析 (x2+x+y)5表示5个因式(x2+x+y)的乘积,要得到含x5y2的项,只需从5个因式中选2个因式取x2,1个因式取x,其余2个因式取y即可,故x5y2的系数为C52C31C22=30.
命题点2 二项式系数与项的系数的问题
角度1 二项展开式中的系数和问题
例4 [多选]已知(1-2x)2 023=a0+a1x+a2x2+…+a2 023x2 023,则下列结论正确的是( ACD )
A.展开式中所有项的二项式系数的和为22 023
B.展开式中所有奇次项的系数的和为32 023+12
C.展开式中所有偶次项的系数的和为32 023-12
D.a12+a222+a323+…+a2 02322 023=-1
解析 对于A,(1-2x)2 023的展开式中所有项的二项式系数的和为22 023,故A正确;对于B,令f(x)=(1-2x)2 023,则a0+a1+a2+a3+…+a2 023=f(1)=-1,a0-a1+a2-a3+…-a2 023=f(-1)=32 023,所以展开式中所有奇次项的系数的和为f(1)-f(-1)2=-32 023+12,展开式中所有偶次项的系数的和为f(1)+f(-1)2=32 023-12,故B错误,C正确;对于D,a0=f(0)=1,a12+a222+a323+…+a2 02322 023=f(12)-a0=-1,故D正确.故选ACD.
方法技巧
应用赋值法求项的系数和问题
(1)对形如(ax+by)n(a,b∈R,n∈N*)的式子求其展开式中的各项系数之和,只需令x=y=1即可;求系数之差时,只需根据题目要求令x=1,y=-1或x=-1,y=1即可.
(2)对(a+bx)n=a0+a1x+a2x2+…+anxn,令f(x)=(a+bx)n,则(a+bx)n的展开式中各项系数之和为f(1),偶次项系数之和为a0+a2+a4+…=f(1)+f(-1)2,奇次项系数之和为a1+a3+a5+…=f(1)-f(-1)2.
角度2 与二项展开式中的系数有关的最值问题
例5 (1)[全国卷Ⅰ]设m为正整数,(x+y)2m展开式的二项式系数的最大值为a,(x+y)2m+1展开式的二项式系数的最大值为b,若13a=7b,则m=( B )
A.5B.6C.7D.8
解析 根据二项式系数的性质,知(x+y)2m展开式中二项式系数的最大值为C2mm,而(x+y)2m+1展开式中二项式系数的最大值为C2m+1m,则C2mm=a,C2m+1m=b.又13a=7b,所以13C2mm=7C2m+1m,即13×(2m)!m!×m!=7×(2m+1)!(m+1)!×m!,解得m=6.
(2)已知(x+124x)n(n≥2)的展开式中,前三项的系数成等差数列,则展开式中系数最大的项是 7x52和7x74 .
解析 展开式中前三项的系数分别是1,n2,18n(n-1),由题意知,2×n2=1+18n(n-1),解得n=8或n=1(舍去).
于是展开式的通项Tk+1=C8k·(x)8-k·(124x)k=C8k·2-k·x4-34k,所以第k+1项的系数是C8k·2-k,第k项的系数是C8k-1·2-k+1,第k+2项的系数是C8k+1·2-k-1.若第k+1项的系数最大,则C8k·2-k≥C8k-1·2-k+1且C8k·2-k≥C8k+1·2-k-1,解得2≤k≤3.又k∈Z,因此k=2或k=3.故系数最大的项是T3=C82·2-2·x4-34×2=7x52和T4=C83·2-3·x4-34×3=7x74.
方法技巧
1.二项式系数最值的求法
当n是偶数时,第n2+1项的二项式系数最大,最大值为Cnn2;当n是奇数时,第n+12项和第n+32项的二项式系数相等,且同时取得最大值,最大值为Cnn-12或Cnn+12.
2.项的系数最值的求法
设展开式各项的系数分别为A1,A2,…,An+1,且第k项系数最大,解不等式组Ak≥Ak-1,Ak≥Ak+1,求出k即可得结果.
训练2 (1)[多选]已知二项式(x-2x)8,则下列结论正确的是( AB )
A.第5项的二项式系数最大
B.所有项的系数之和为1
C.有且仅有第6项的系数的绝对值最大
D.展开式中共有4项有理项
解析 由题意知,展开式中共有9项,二项式系数最大的项为第5项,A正确;所有项的系数和为(1-2)8=1,B正确;Tr+1=C8rx8-r·(-2x)r=(-2)rC8rx8-3r2,r=0,1,2,…,8,显然r=0,2,4,6,8时,Tr+1是有理项,所以共有5项有理项,D错误;由2rC8r≥2r+1C8r+1,2rC8r≥2r-1C8r-1,得18-r≥2r+1,2r≥19-r,解得5≤r≤6,所以r=5或r=6,故第6项和第7项的系数的绝对值最大,C错误.故选AB.
(2)[2022浙江]已知多项式(x+2)(x-1)4=a0+a1x+a2x2+a3x3+a4x4+a5x5,则a2= 8 ,a1+a2+a3+a4+a5= -2 .
解析 由多项式展开式可知,a2=2C42(-1)2+C43(-1)3=12-4=8.令x=0可得a0=2,令x=1可得a0+a1+a2+a3+a4+a5=0,所以a1+a2+a3+a4+a5=-2.
命题点3 二项式定理的综合应用
例6 (1)利用二项式定理计算1.056,则其结果精确到0.01的近似值是( D )
解析 1.056=(1+0.05)6=C60+C61×0.05+C62×0.052+C63×0.053+…=1+0.3+0.037 5+0.002 5+…≈1.34.
(2)设a∈N,且0≤a<26,若51 2 020+a能被13整除,则a的值为( D )
A.0 B.11或0C.12D.12或25
解析 ∵512 020+a=(52-1)2 020+a=C2 0200522 020(-1)0+C2 0201522 019(-1)1+C2 0202522 018(-1)2+…+C2 0202 019521·(-1)2 019+C2 0202 020(-1)2 020+a,又52能被13整除,∴需使C2 0202 020(-1)2 020+a能被13整除,即1+a能被13整除,∴1+a=13k,k∈Z,又0≤a<26,∴a=12或a=25,故选D.
方法技巧
二项式定理应用的常见题型及解题策略
训练3 (1)设复数x=2i1-i(i是虚数单位),则C2 0241x+C2 0242x2+C2 0243x3+…+C2 0242 024x2 024=( A )
A.0B.-2 C.-1+iD.-1-i
解析 x=2i1-i=2i(1+i)(1-i)(1+i)=-1+i,则C2 0241x+C2 0242x2+C2 0243x3+…+C2 0242 024x2 024=(1+x)2 024-1=i2 024-1=1-1=0.
(2)若(2x+1)100=a0+a1x+a2x2+…+a100x100,则2(a1+a3+a5+…+a99)-3除以8的余数为 5 .
解析 令x=1,得a0+a1+a2+…+a100=3100.令x=-1,得a0-a1+a2-…+a100=1,两式相减得2(a1+a3+a5+…+a99)=3100-1,则2(a1+a3+a5+…+a99)-3=3100-4.3100-4=950-4=(8+1)50-4=C500×850+C501×849+…+C5049×8+C5050-4=C500×850+C501×849+…+C5049×8-3=C500×850+C501×849+…+C5049×8-8+5,则C500×850+C501×849+…+C5049×8-8+5除以8的余数为5,即2(a1+a3+a5+…+a99)-3除以8的余数为5.
1.[命题点1角度1/2022天津高考](x+3x2)5的展开式中常数项为 15 .
解析 (x+3x2)5展开式的通项公式为Tk+1=C5k(x)5-k(3x2)k=3kC5kx5-5k2,令5-5k2=0,得k=1,所以常数项为3×C51=15.
2.[命题点1角度2/全国卷Ⅲ](1+2x2)(1+x)4的展开式中x3的系数为( A )
A.12B.16C.20D.24
解析 (1+x)4的展开式的通项公式为Tr+1=C4r14-rxr(r=0,1,2,3,4).
(1+2x2)(1+x)4的展开式中含x3的项的系数为1×(C43×11)+2×(C41×13)=12.故选A.
3.[命题点1角度3/2023湖南长沙第一中学段考](x-2y+z)8的展开式中x3y3z2的系数是 -4 480 (用数字作答).
解析 (x-2y+z)8可看成8个(x-2y+z)相乘,在8个(x-2y+z)中的3个式子中取x,3个式子中取-2y,剩下的2个式子中取z,则(x-2y+z)8的展开式中x3y3z2的系数是C83×C53×(-2)3×C22=-4 480.
4.[命题点2角度1/2022北京高考]若(2x-1)4=a4x4+a3x3+a2x2+a1x+a0,则a0+a2+a4=( B )
A.40B.41C.-40D.-41
解析 依题意,令x=1,可得1=a4+a3+a2+a1+a0,令x=-1,可得81=a4-a3+a2-a1+a0,以上两式相
加可得82=2(a4+a2+a0),所以a0+a2+a4=41,故选B.
5.[命题点3]今天是星期二,经过7天后还是星期二,那么经过22 021天后是( D )
A.星期三B.星期四
C.星期五D.星期六
解析 22 021=4×22 019=4×8673=4×(7+1)673=4×(C6730×7673+C6731×7672+…+C673672×7+C673673),由于括号中,除了最后一项外,其余各项都能被7整除,故整个式子除以7的余数为4C673673=4,故经过22 021天后是星期六,故选D.
6.[命题点3]已知-C1001(2-x)+C1002(2-x)2-C1003(2-x)3+…+C100100(2-x)100=a0+a1x+a2x2+…+a100x100,则a1+a2+a3+…+a99的值是 -2 .
解析 记f(x)=1-C1001(2-x)+C1002(2-x)2-C1003(2-x)3+…+C100100(2-x)100-1=[1-(2-x)]100-1=(x-1)100-1=a0+a1x+a2x2+…+a100x100.令x=1,得a0+a1+a2+…+a100=-1.令x=0,得a0=0,又易知a100=1,所以a1+a2+a3+…+a99=-2.
7.[命题点3]0.996的计算结果精确到0.001的近似值是( B )
解析 0.996=(1-0.01)6=C60×1-C61×0.01+C62×0.012-C63×0.013+…+C66×0.016=1-0.06+0.001 5-0.000 02+…+0.016≈0.941.
学生用书·练习帮P384
1.[2024河北保定部分示范高中统考](9x+8x)5的展开式中含x2的项的系数为( D )
A.C52×92×83B.C54×9×84
C.C51×94×8D.C52×93×82
解析 (9x+8x)5的二项展开式的通项Tr+1=C5r(9x)5-r·(8x-12)r=C5r·95-r·8r·x5-32r,0≤r≤5,r∈N,令5-32r=2,得r=2,所以展开式中含x2的项为T2+1=C52×93×82x2,其系数为C52×93×82.故选D.
2.[2024湖北武汉第四十九中模拟](1+x+x2)(1-x)10的展开式中x5的系数为( D )
A.120B.135C.-140D.-162
解析 (1-x)10展开式的通项为Tr+1=C10r(-x)r=(-1)r·C10rxr.
令r=5,则1×(1-x)10展开式中x5的系数为(-1)5C105=-252;
令r=4,则x(1-x)10展开式中x5的系数为(-1)4C104=210;
令r=3,则x2(1-x)10展开式中x5的系数为(-1)3C103=-120.
∴(1+x+x2)(1-x)10的展开式中x5的系数为-252+210-120=-162.故选D.
3.[2024陕西宝鸡金台区统考]若(x-1x)n的展开式中第3项与第9项的二项式系数相等,则展开式中二项式系数最大的项为( C )
A.第4项B.第5项C.第6项D.第7项
解析 由二项式定理可得展开式中第3项与第9项的二项式系数分别为Cn2和Cn8,即Cn2=Cn8,解得n=10.因此展开式中二项式系数最大的项为C105x5(-1x)5,是第6项,故选C.
4.[2024山东青岛一中统考]若(x+mx)(x-1x)5的展开式中常数项是10,则m=( D )
A.-2B.-1C.1D.2
解析 (x+mx)(x-1x)5=x(x-1x)5+mx(x-1x)5.
(x-1x)5的展开式的通项为Tr+1=C5rx5-r(-1x)r=C5r·(-1)rx5-2r.令5-2r=-1,解得r=3,则x(x-1x)5的展开式的常数项为-C53=-10,
令5-2r=1,解得r=2,则mx(x-1x)5的展开式的常数项为mC52=10m.
因为(x+mx)(x-1x)5的展开式中常数项是10,所以10m-10=10,解得m=2,故选D.
5.[多选/2024青岛市检测]已知(2x-1x)n的展开式中各二项式系数的和为256,则( ABD )
A.n=8
B.展开式中x-2的系数为-448
C.展开式中常数项为16
D.展开式中所有项的系数和为1
解析 因为(2x-1x)n的展开式中各二项式系数的和为256,所以2n=256,解得n=8,选项A正确;
(2x-1x)8的展开式的通项公式为Tk+1=C8k(2x)8-k·(-1x)k=(-1)k28-kC8kx8-2k,令8-2k=-2,解得k=5,所以展开式中x-2的系数为(-1)5×23×C85=-448,所以选项B正确;
令8-2k=0,解得k=4,所以展开式中常数项为(-1)4×24×C84=1 120,所以选项C错误;
令x=1,得(2x-1x)8=1,所以展开式中所有项的系数和为1,所以选项D正确.综上,选ABD.
6.[多选/2024江苏连云港统考]已知(1-2x)6=a0+a1x+a2x2+…+a6x6,则下列选项正确的是( AC )
A.a0=1
B.a2=120
C.|a0|+|a1|+|a2|+…+|a6|=729
D.a1+a2+…+a5=0
解析
7.二项式(2x2-14x)6的展开式的中间项是 -52x3 .
解析 二项式展开式的通项为Tk+1=C6k(2x2)6-k·(-14x)k=(-14)k26-kC6kx12-3k,二项式展开式一共有7项,所以第4项为中间项,即k=3,T4=(-14)326-3·C63x12-3×3=-52x3.
8.[2024吉林一中、东北师大附中等校联考](x2-x+1)5的展开式中,x5的系数为 -51 .
解析 (x2-x+1)5可以看作5个因式(x2-x+1)相乘,要想得到含x5的项,可分三种情况:
①5个因式中选2个因式取x2,1个因式取-x,2个因式取1;
②5个因式中选1个因式取x2,3个因式取-x,1个因式取1;
③5个因式中都取-x.
所以展开式中含x5的项为C52·(x2)2·C31·(-x)·C22·12+C51·x2·C43·(-x)3·1+C55·(-x)5=-51x5,
所以x5的系数为-51.
9.[2023湖北十堰6月统考](2x+11)10的展开式中系数最大的项是第 10 项.
解析 (2x+11)10展开式的通项为Tr+1=C10r·(2x)10-r11r=C10r·210-r·11r·x10-r,由C10r·210-r·11r≥C10r-1·211-r·11r-1,C10r·210-r·11r≥C10r+1·29-r·11r+1,得10813≤r≤12113,因为r∈N,所以r=9,故系数最大的项是第10项.
10. S=C271+C272+…+C2727除以9的余数为 7 .
解析 依题意S=C271+C272+…+C2727=227-1=89-1=(9-1)9-1=C90×99-C91×98+…+C98×9-C99-1=9×(C90×98-C91×97+…+C98)-2.∵C90×98-C91×97+…+C98是正整数,∴S被9除的余数为7.
11.[开放题]写出一个正整数n,使得(1x2+x)n的展开式中存在常数项,则n可以是 5(答案不唯一,n=5k,k∈N*均可) .
解析 二项式(1x2+x)n的展开式的通项Tr+1=Cnr·(1x2)n-r·(x)r=Cnr·x5r-4n2,若该展开式中存在常数项,则方程5r-4n=0有解,故可取n=5,r=4.
12.若x8=a0+a1(x+1)+a2(x+1)2+…+a8(x+1)8,则a3= -56 .
解析 令x+1=t,则x=t-1,所以x8=a0+a1(x+1)+a2(x+1)2+…+a8(x+1)8可转化为(t-1)8=a0+a1t+a2t2+…+a8t8,即(1-t)8=a0+a1t+a2t2+…+a8t8,所以a3=-C83=-56.
13.(1+x)2+(1+x)3+…+(1+x)9的展开式中x2的系数是( D )
A.60B.80
C.84D.120
解析 因为(1+x)n的展开式的通项Tr+1=Cnrxr,所以(1+x)2+(1+x)3+…+(1+x)9的展开式中x2的系数是C22+C32+C42+…+C92=C33+C32+C42+…+C92=C43+C42+…+C92=C53+C52+…+C92=…=C93+C92=C103=10×9×83×2×1=120(组合数性质Cn+1m=Cnm+Cnm-1,n,m∈N*,且m≤n的应用).
14.[多选/2024湖南师范大学附中模拟]已知(ax+1x2)10(a>0)的展开式的各项系数之和为1 024,则展开式中( BCD )
A.奇数项的二项式系数和为256
B.第6项的系数最大
C.存在常数项
D.有理项共有6项
解析 令x=1,得(a+1)10=1 024,则a=1或a=-3(舍去).∴(x+1x2)10的展开式的通项为Tr+1=C10r(x)10-r·(1x2)r=C10rx5-52r.
15.(1-x)6(1+x)4的展开式中x的系数是 -3 .
解析 解法一 (1-x)6的展开式的通项为C6m(-x)m=C6m(-1)mxm2,1+x4的展开式的通项为C4n(x)n=C4nxn2,
则(1-x)6(1+x)4的展开式的通项为C6m(-1)mC4nxm2+n2,其中m=0,1,2,…,6,n=0,1,2,3,4.
令m2+n2=1,得m+n=2,
于是(1-x)6(1+x)4的展开式中x的系数等于C60·(-1)0·C42+C61·(-1)1·C41+C62·(-1)2·C40=-3.
解法二 (1-x)6(1+x)4=[(1-x)(1+x)]4(1-x)2=(1-x)4(1-2x+x),于是(1-x)6(1+x)4的展开式中x的系数为C40·1+C41·(-1)1·1=-3.
16.[2023成都模拟](5-3x+2y)n展开式中不含y的项的系数和为64,则展开式中的常数项为 15 625 .
解析 (5-3x+2y)n展开式中不含y的项,即展开式中y的指数为0,即(5-3x)n的展开式,再令x=1,得(5-3x+2y)n展开式中不含y的项的系数和为(5-3)n=64,
∴n=6,由(5-3x+2y)6=[5-(3x-2y)]6,得展开式中的常数项为C60×56=15 625.
17.[数学文化]“杨辉三角”揭示了二项式系数在三角形中的一种几何排列规律,最早在我国南宋数学家杨辉1261年所著的《详解九章算法》一书中出现.“杨辉三角”是中国数学史上的一个伟大成就,激发了一批又一批数学爱好者的探究欲望.如图,由“杨辉三角”,下列叙述正确的是( D )
杨辉三角
第0行 1
第1行 1 1
第2行1 2 1
第3行 1 3 3 1
第4行 1 4 6 4 1
第5行1 5 10 10 5 1
第6行 1 6 15 20 15 6 1
第7行 1 7 21 35 35 21 7 1
第8行 1 8 28 56 70 56 28 8 1
︙ ︙
A.C32+C42+C52+…+C92=120
B.第2 023行中从左往右第1 013个数与第1 014个数相等
C.记第n行的第i个数为ai,则∑i=1n+12i-1ai=4n
D.第20行中第8个数与第9个数之比为8∶13
解析 根据题意,由“杨辉三角”可得,第n行的第r个数为Cnr-1,由此分析选项.
18.[综合创新/多选]设k∈R且k≠0,n≥2,n∈N*,(1+kx)n=a0+a1x+a2x2+…+anxn,则( BC )
A.∑i=0nai=2n
B.∑i=1nai=(1+k)n-1
C.∑i=1niai=nk(1+k)n-1
D.∑i=2ni2ai=2n(n-1)k2(1+k)n-2
解析 对于A,在(1+kx)n=a0+a1x+a2x2+…+anxn中令x=1,得∑i=0nai=(1+k)n,故A错误;
对于B,在(1+kx)n=a0+a1x+a2x2+…+anxn中令x=0得a0=1,所以∑i=1nai=(1+k)n-1,故B正确;
对于C,(1+kx)n=a0+a1x+a2x2+…+anxn两边同时求导,得nk(1+kx)n-1=a1+2a2x+…+nanxn-1 (*),
令x=1得∑i=1niai=nk(1+k)n-1,故C正确;
对于D,(*)式两边同时求导得nk2(n-1)(1+kx)n-2=2a2+6a3x+…+n(n-1)anxn-2,
令x=1,得∑i=2ni(i-1)ai=nk2(n-1)(1+k)n-2,所以∑i=2ni2ai=∑i=2ni(i-1)ai+∑i=2niai=nk2(n-1)(1+k)n-2+nk(1+k)n-1-a1=nk(nk+1)(1+k)n-2-k,(由对B的分析得a1=k)
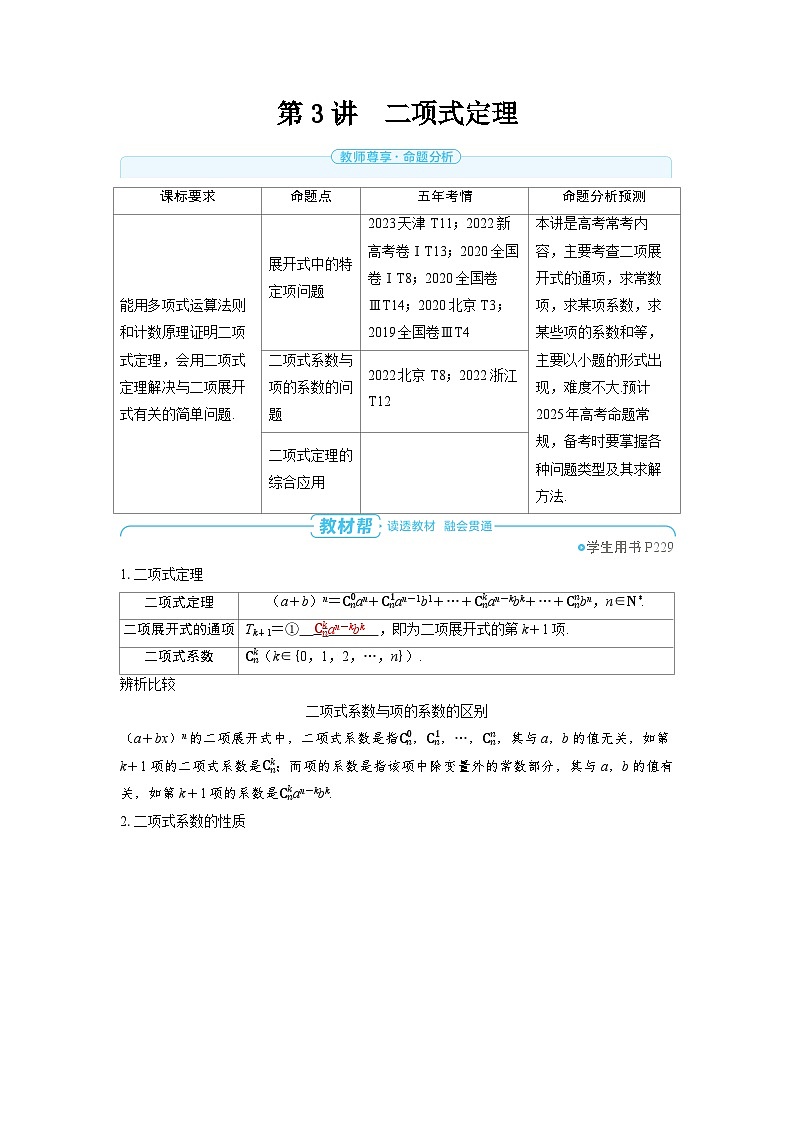
故D不正确.综上所述,故选BC.课标要求
命题点
五年考情
命题分析预测
能用多项式运算法则和计数原理证明二项式定理,会用二项式定理解决与二项展开式有关的简单问题.
展开式中的特定项问题
2023天津T11;2022新高考卷ⅠT13;2020全国卷ⅠT8;2020全国卷ⅢT14;2020北京T3;2019全国卷ⅢT4
本讲是高考常考内容,主要考查二项展开式的通项,求常数项,求某项系数,求某些项的系数和等,主要以小题的形式出现,难度不大.预计2025年高考命题常规,备考时要掌握各种问题类型及其求解方法.
二项式系数与项的系数的问题
2022北京T8;2022浙江T12
二项式定理的综合应用
二项式定理
(a+b)n=Cn0an+Cn1an-1b1+…+Cnkan-kbk+…+Cnnbn,n∈N*.
二项展开式的通项
Tk+1=① Cnkan-kbk ,即为二项展开式的第 k+1项.
二项式系数
Cnk(k∈{0,1,2,…,n}).
因式分解法
通过分解因式将三项式变成两个二项式的积的形式,然后用二项式定理分别展开.
逐层展开法
将三项式分成两组,用二项式定理展开,再把其中含两项的一组展开,从而解决问题.
利用组合知识
把三项式(a+b+c)n(n∈N*)看成n个a+b+c的积,然后利用组合知识求解.
题型
解题策略
近似计算
先观察精确度,然后选取展开式中若干项求解.
证明整除问
题或求余数
将被除式(数)合理的变形,拆成二项式,使被除式(数)展开后的每一项都含有除式的因式.
逆用二项
式定理
根据所给式子的特点结合二项展开式的要求,变形使之具备二项式定理右边的结构,然后逆用二项式定理求解.
选项
分析过程
正误
A
令x=0,则1=a0
√
B
(1-2x)6展开式的通项为Tr+1=C6r(-2x)r=C6r·(-2)rxr,所以令r=2可得a2=C62(-2)2=60
✕
C
当r=1,3,5时,可得a1,a3,a5<0,同理可得a0,a2,a4,a6>0,所以令x=-1,得36=a0-a1+a2-a3+a4-a5+a6,所以|a0|+|a1|+|a2|+…+|a6|=a0-a1+a2-a3+a4-a5+a6=36=729
√
D
令r=6,可得a6=C66(-2)6=64,由A知a0=1.令x=1,则1=a0+a1+a2+a3+a4+a5+a6,所以a1+a2+…+a5=1-64-1=-64
✕
选项
分析过程
正误
A
奇数项的二项式系数和为12(C100+C101+…+C1010)=12×210=512
✕
B
由题意知展开式共11项,故第6项的系数最大
√
C
令5-52r=0,解得r=2,故存在常数项,且常数项为第3项
√
D
当r=0,2,4,6,8,10时,为有理项,故有理项共有6项
√
选项
分析过程
正误
A
C32+C42+…+C92=C33+C32+C42+…+C92-1=C103-1=119
✕
B
第2 023行中从左往右第1 013个数为C2 0231 012,第1 014个数为C2 0231 013,两者不相等
✕
C
记第n行的第i个数为ai,则ai=Cni-1,
则∑i=1n+12i-1×ai=∑i=1n+12i-1Cni-1×1n-i+1=(1+2)n=3n
✕
D
第20行中第8个数为C207,第9个数为C208,则两个数的比为C207∶C208=20!7!×13!∶20!8!×12!=8∶13
√
2025年高考数学精品教案第十章 计数原理 概率 随机变量及其分布 第5讲 事件的相互独立性、条件概率与全概率公式: 这是一份2025年高考数学精品教案第十章 计数原理 概率 随机变量及其分布 第5讲 事件的相互独立性、条件概率与全概率公式,共16页。
2025年高考数学精品教案第十章 计数原理 概率 随机变量及其分布 突破1 概率、统计中的开放性与决策问题: 这是一份2025年高考数学精品教案第十章 计数原理 概率 随机变量及其分布 突破1 概率、统计中的开放性与决策问题,共10页。
2025年高考数学精品教案第十章 计数原理 概率 随机变量及其分布 突破2 概率与统计的综合: 这是一份2025年高考数学精品教案第十章 计数原理 概率 随机变量及其分布 突破2 概率与统计的综合,共17页。












