
- 高考数学一轮复习《考点•题型•技巧》精讲与精练高分突破系列(新高考专用)4.3三角函数的图象与性质(原卷版+解析) 试卷 0 次下载
- 高考数学一轮复习《考点•题型•技巧》精讲与精练高分突破系列(新高考专用)4.6正、余弦定理及其应用举例(原卷版+解析) 试卷 0 次下载
- 高考数学一轮复习《考点•题型•技巧》精讲与精练高分突破系列(新高考专用)6.1数列的概念及通项公式(原卷版+解析) 试卷 0 次下载
- 高考数学一轮复习《考点•题型•技巧》精讲与精练高分突破系列(新高考专用)6.3等比数列(原卷版+解析) 试卷 0 次下载
- 高考数学一轮复习《考点•题型•技巧》精讲与精练高分突破系列(新高考专用)7.1不等式的性质(原卷版+解析) 试卷 0 次下载
高考数学一轮复习《考点•题型•技巧》精讲与精练高分突破系列(新高考专用)4.4函数y=Asin(ωx+φ)的图象与性质(原卷版+解析)
展开图
知识点总结
1.用“五点法”画y=Asin(ωx+φ)(A>0,ω>0,|φ|
3.函数y=Asin(ωx+φ)的有关概念
[常用结论]
1.函数y=Asin(ωx+φ)+k图象平移的规律:“左加右减,上加下减”.
2.由y=sin ωx到y=sin(ωx+φ)(ω>0,φ>0)的变换:向左平移eq \f(φ,ω)个单位长度而非φ个单位长度.
典型例题分析
考向一 公式的逆用及变形
角度1 公式的活用
例1 (1)(2023·濮阳一模)cs 40°sin 70°-sin 40°·sin 160°=( )
A.-eq \f(1,2) B.eq \f(1,2)
C.-eq \f(\r(3),2) D.eq \f(\r(3),2)
(2)若α+β=-eq \f(3π,4),则(1+tan α)(1+tan β)=________.
角度2 辅助角公式的运用
例2 化简:(1)sin eq \f(π,12)-eq \r(3)cs eq \f(π,12);(2)eq \f(1,sin 10°)-eq \f(\r(3),sin 80°).
感悟提升 三角函数公式活用技巧
(1)逆用公式应准确找出所给式子与公式的异同,创造条件逆用公式.
(2)tan αtan β,tan α+tan β(或tan α-tan β),tan(α+β)(或tan(α-β))三者中可以知二求一.应注重公式的逆用和变形使用.
考向二 三角函数式的化简
例3 (1)化简:eq \f(2cs4x-2cs2x+\f(1,2),2tan\b\lc\(\rc\)(\a\vs4\al\c1(\f(π,4)-x))sin2\b\lc\(\rc\)(\a\vs4\al\c1(\f(π,4)+x)))=________.
(2)化简:(eq \f(1,tan \f(α,2))-tan eq \f(α,2))·eq \b\lc\(\rc\)(\a\vs4\al\c1(1+tan α·tan \f(α,2)))=________.
感悟提升 1.三角函数式的化简要遵循“三看”原则:一看角,二看名,三看式子结构与特征.
2.三角函数式的化简要注意观察条件中角之间的联系(和、差、倍、互余、互补等),寻找式子和三角函数公式之间的共同点.
考向三 三角函数求值问题
角度1 给角求值
例4 (1)sin 40°(tan 10°-eq \r(3))等于( )
A.2 B.-2
C.1 D.-1
(2)cs 20°·cs 40°·cs 100°=________.
角度2 给值求值
例5 (1)(2023·安徽名校联考)已知cseq \b\lc\(\rc\)(\a\vs4\al\c1(α+\f(π,6)))=eq \f(3,4),则sineq \b\lc\(\rc\)(\a\vs4\al\c1(2α+\f(5π,6)))=( )
A.-eq \f(1,8) B.eq \f(1,8)
C.-eq \f(1,4) D.eq \f(1,4)
(2)(2023·铁岭质检)已知eq \f(1,cs θ)+tan θ=2,则tan eq \f(θ,2)的值为( )
A.3 B.eq \f(1,3)或-1
C.eq \f(1,2) D.eq \f(1,3)
角度3 给值求角
例6 已知α,β均为锐角,cs α=eq \f(2\r(7),7),sin β=eq \f(3\r(3),14),则cs 2α=________
2α-β=________.
感悟提升 1.给值(角)求值问题求解的关键在于“变角”,使其角相同或具有某种关系,借助角之间的联系寻找转化方法.
2.给值(角)求值问题的一般步骤
(1)化简条件式子或待求式子;
(2)观察条件与所求之间的联系,从函数名称及角入手;
(3)将已知条件代入所求式子,化简求值.
考向四 三角恒等变换的应用
例7 设函数f(x)=sin x+cs x(x∈R).
(1)求函数y=eq \b\lc\[\rc\](\a\vs4\al\c1(f\b\lc\(\rc\)(\a\vs4\al\c1(x+\f(π,2)))))eq \s\up12(2)的最小正周期;
(2)求函数y=f(x)feq \b\lc\(\rc\)(\a\vs4\al\c1(x-\f(π,4)))在eq \b\lc\[\rc\](\a\vs4\al\c1(0,\f(π,2)))上的最大值.
感悟提升 三角恒等变换的综合应用主要是将三角变换与三角函数的性质相结合,通过变换把函数化为f(x)=Asin(ωx+φ)+b的形式再研究其性质,解题时注意观察角、函数名、结构等特征,注意利用整体思想解决相关问题.
考向五 函数y=Asin(ωx+φ)的图象及变换
例8已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,-eq \f(π,2)<φ
(2)作出f(x)在[0,π]上的图象(要列表);
(3)函数y=f(x)的图象可由函数y=sin x的图象经过怎样的变换得到?
迁移 本例已知条件不变,第(3)问改为:函数y=f(x)的图象可由函数y=cs x的图象经过怎样的变换得到?
感悟提升 作函数y=Asin(ωx+φ)(A>0,ω>0)的图象常用如下两种方法:
(1)五点法作图,用“五点法”作y=Asin(ωx+φ)的简图,主要是通过变量代换,设z=ωx+φ,由z取0,eq \f(π,2),π,eq \f(3,2)π,2π来求出相应的x,通过列表,计算得出五点坐标,描点后得出图象;
(2)图象的变换法,由函数y=sin x的图象通过变换得到y=Asin(ωx+φ)的图象有两种途径:“先平移后伸缩”与“先伸缩后平移”.
基础题型训练
一、单选题
1.要得到函数的图象,只需将函数的图象上的所有点沿轴
A.向右平移1个单位长度B.向左平移3个单位长度
C.向左平移1个单位长度D.向右平移3个单位长度
2.把函数的图象向右平移个单位,得到的函数解析式为
A.B.
C.D.
3.已知函数的图象向右平移个单位长度,则平移后图象的对称中心为( )
A.B.
C.D.
4.函数 在一个周期内的图像如图所示,则此函数的解析式为( )
A.B.
C.D.
5.将函数的图象上所有的点向右平行移动个单位长度,再把所得各点的横坐标伸长到原来的倍(纵坐标不变),所得图象的函数解析式是( )
A.B.
C.D.
6.已知函数,若在上有且只有3个零点,则的取值范围为( )
A.B.C.D.
二、多选题
7.要得到函数的图象,只需将函数图象上所有点的坐标( )
A.向右平移个单位长度,再将横坐标缩短到原来的倍(纵坐标不变)
B.向左平移个单位长度,再将横坐标缩短到原来的倍(纵坐标不变)
C.横坐标缩短到原来的倍(纵坐标不变),再向左平移个单位长度
D.横坐标缩短到原来的倍(纵坐标不变),再向右平移个单位长度
8.已知函数的部分图像如图所示,将的图像向右平移个单位后,得到函数的图像,若对于任意的,则值可以为( )
A.B.C.D.
三、填空题
9.在平面直角坐标系中,将曲线上每一点的横坐标保持不变,纵坐标变为原来的倍,所得新的曲线方程为__________.
10.若将函数的图象沿轴向右平移个单位后所得的图象与的图象关于轴对称,则的最小值为________________.
11.已知 ,若对任意 ,都有,则的最大值为________.
12.下列四个命题:
①函数的值域是,则函数的值域为;
②把函数图像上的每一个点的横坐标伸长到原来的4倍,然后再向右平移个单位得到的函数解析式为;
③已知,则与共线的单位向量为;
④一条曲线和直线的公共点个数是m,则m的值不可能是1.
其中正确的有___________(写出所有正确命题的序号).
四、解答题
13.函数的图像可以通过函数的图像经过怎样的平移得到?解释你的结论.
14.已知函数(,,)的一段图像如下图所示,
(1)求函数的解析式;
(2)求函数的单调增区间;
15.已知函数(,,)的部分图像如图所示.
(1)求函数的解析式;
(2)求不等式的解集.
16.设函数,其中,已知
(1)求;
(2)将函数的图像上的各点的横坐标伸长为原来的2倍(纵坐标不变),再将得到的图像向右平移个单位长度,得到函数的图像上,求在上的最小值.
提升题型训练
一、单选题
1.要得到函数,的图像,只需把函数,的图像( )
A.向右平移个单位B.向右平移个单位
C.向左平移个单位D.向左平移个单位
2.将函数的图象向右平移个单位长度,得到函数的图象,若函数在上单调递增,则的最大值为( )
A.2B.C.D.4
3.要得到函数的图象,只需将函数的图象( ).
A.向右平移个单位B.向左平移个单位C.向左平移个单位D.向右平移个单位
4.已知函数(其中),若对任意,存在,使得,则的取值范围为( )
A.B.C.D.
5.已知函数的最小正周期为,将其图象向右平移个单位后得函数的图象,则函数的图象
A.关于直线对称B.关于直线对称
C.关于点对称D.关于点对称
6.函数(其中,)的图象如图所示,为了得到的图象,则需将的图象( )
A.横坐标缩短到原来的,再向右平移个单位
B.横坐标缩短到原来的,再向右平移个单位
C.横坐标伸长到原来的倍,再向右平移个单位
D.横坐标伸长到原来的倍,再向右平移个单位
二、多选题
7.下列说法错误的是( )
A.函数的最小正周期是
B.函数是周期为的奇函数
C.函数最小正周期为
D.若对,满足,,则函数周期为
8.已知函数相邻的最高点的距离为,则下列结论正确的是( )
A.函数的图象关于点中心对称
B.函数在区间上的值域为
C.将函数的图象上所有点的横坐标缩短为原来的,然后向左平移个单位得的图象
D.若,则
三、填空题
9.函数的初相是_________
10.函数f(x)=Asin(ωx+φ)(A,ω,φ为常数,A>0,ω>0)的部分图象如图所示,则的值是_____.
11.将函数的图象向右平移个单位长度得到图像,则下列说法中正确的是______________(填序号).
①函数的最小正周期是; ②图像关于直线对称;
③函数在区间上单调递减; ④图像关于点对称;
12.已知函数,,则下列结论中正确的是______,
①若,则将图象向左平移个单位长度后得到的图象关于原点对称
②若,且的最小值为,则
③若在上单调递增,则的取值范围为
④当时,在有且只有3个零点
四、解答题
13.函数的图像可以通过函数的图像经过怎样的平移得到?解释你的结论.
14.已知函数的最小正周期为,且.
(1)求和的值.
(2)将函数的图象向右平移个单位长度(纵坐标不变),得到函数的图象,
①求函数的单调递增区间;
②求函数在上的最大值.
15.已知函数.
(1)求函数的最大值和最小值,并求取得最大值和最小值时对应的的值;
(2)设方程在区间内有两个相异的实数根,求的值.
16.函数在一个周期内的图象如图所示,为图象的最高点,,为图象与轴的交点,为等边三角形.将函数的图象上各点的横坐标变为原来的倍后,再向右平移个单位,得到函数的图象.
(Ⅰ)求函数的解析式;
(Ⅱ)若不等式对任意恒成立,求实数的取值范围.
x
-eq \f(φ,ω)+eq \f(π,2ω)
eq \f(3π,2ω)-eq \f(φ,ω)
eq \f(2π-φ,ω)
ωx+φ
0
π
2π
y=Asin (ωx+φ)
0
A
0
-A
0
y=Asin(ωx+φ)(A>0,ω>0),x∈[0,+∞)表示一个振动量时
振幅
周期
频率
相位
初相
A
T=eq \f(2π,ω)
f=eq \f(1,T)
=eq \f(ω,2π)
φ
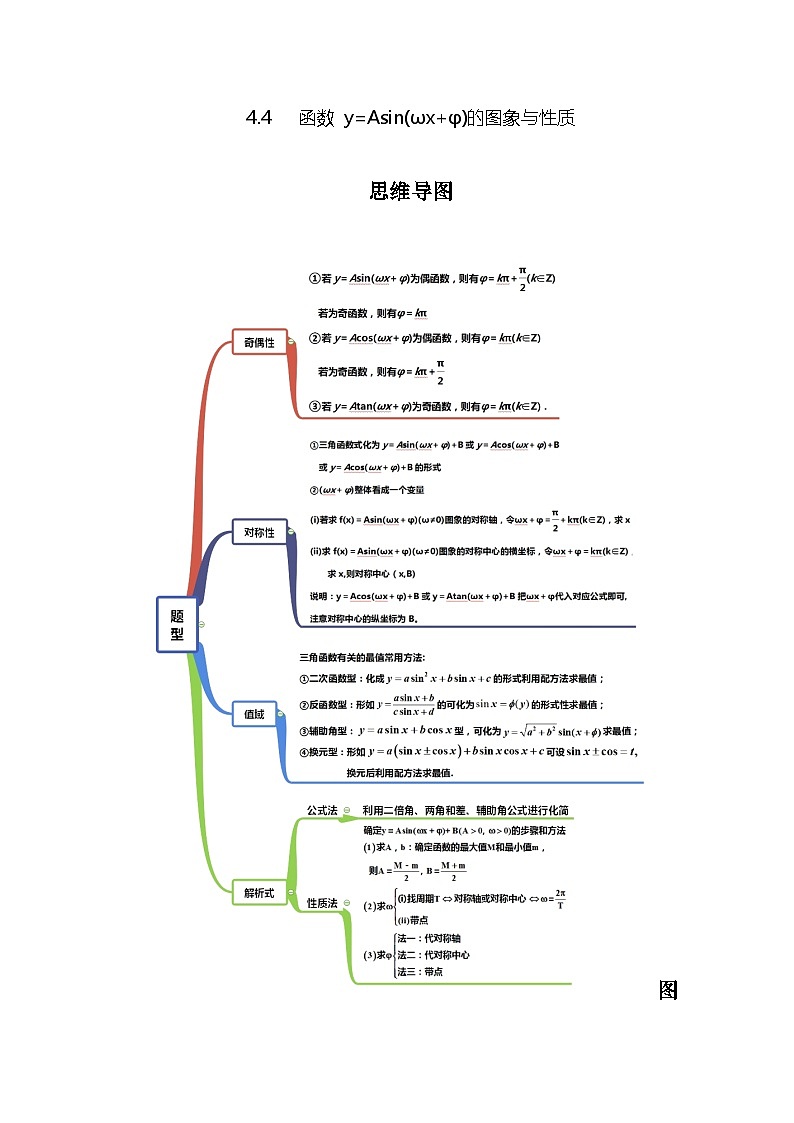
4.4 函数 y=Asin(ωx+φ)的图象与性质
思维导图
图
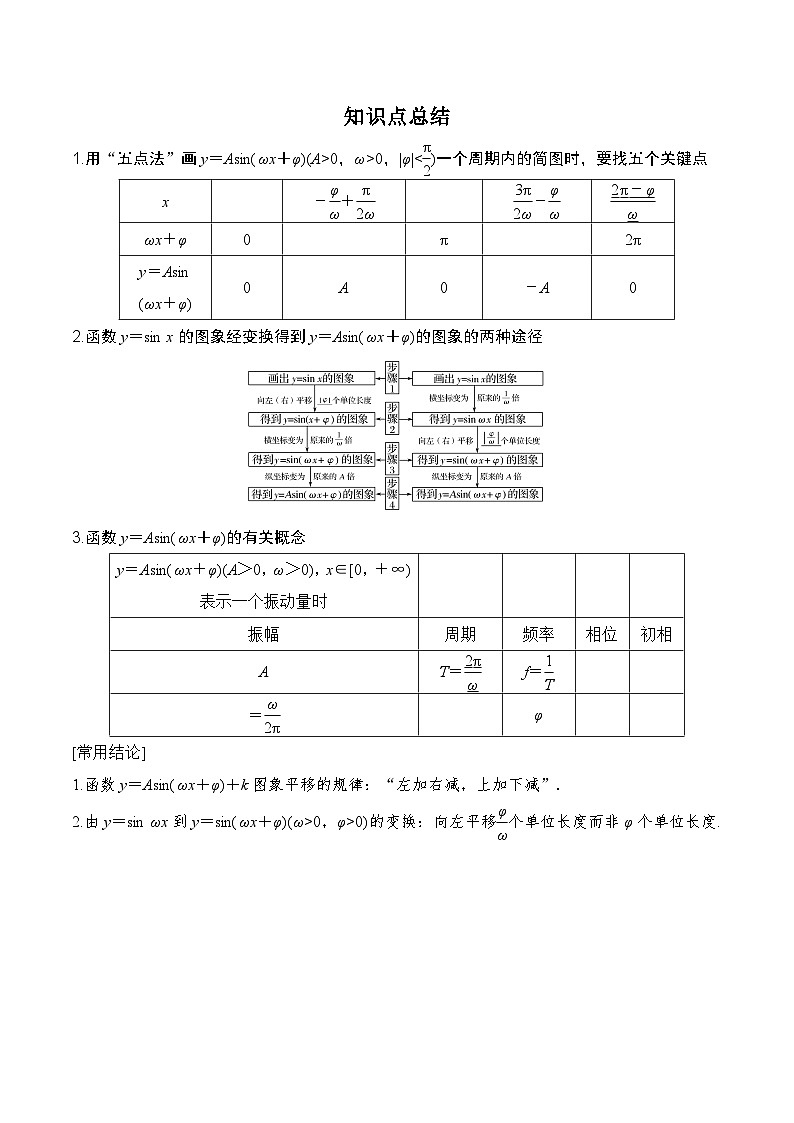
知识点总结
1.用“五点法”画y=Asin(ωx+φ)(A>0,ω>0,|φ|
3.函数y=Asin(ωx+φ)的有关概念
[常用结论]
1.函数y=Asin(ωx+φ)+k图象平移的规律:“左加右减,上加下减”.
2.由y=sin ωx到y=sin(ωx+φ)(ω>0,φ>0)的变换:向左平移eq \f(φ,ω)个单位长度而非φ个单位长度.
典型例题分析
考向一 公式的逆用及变形
角度1 公式的活用
例1 (1)(2023·濮阳一模)cs 40°sin 70°-sin 40°·sin 160°=( )
A.-eq \f(1,2) B.eq \f(1,2)
C.-eq \f(\r(3),2) D.eq \f(\r(3),2)
答案 B
解析 cs 40°sin 70°-sin 40°sin 160°=cs 40°cs 20°-sin 40°sin 20°
=cs(40°+20°)=cs 60°=eq \f(1,2).故选B.
(2)若α+β=-eq \f(3π,4),则(1+tan α)(1+tan β)=________.
答案 2
解析 taneq \b\lc\(\rc\)(\a\vs4\al\c1(-\f(3π,4)))=tan(α+β)=eq \f(tan α+tan β,1-tan αtan β)=1,
所以1-tan αtan β=tan α+tan β,
则1+tan α+tan β+tan αtan β=2,
即(1+tan α)·(1+tan β)=2.
角度2 辅助角公式的运用
例2 化简:(1)sin eq \f(π,12)-eq \r(3)cs eq \f(π,12);(2)eq \f(1,sin 10°)-eq \f(\r(3),sin 80°).
解 (1)法一 原式=2eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,2)sin \f(π,12)-\f(\r(3),2)cs \f(π,12)))
=2eq \b\lc\(\rc\)(\a\vs4\al\c1(sin \f(π,6)sin \f(π,12)-cs \f(π,6)cs \f(π,12)))=-2cseq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,6)+\f(π,12)))=-2cs eq \f(π,4)=-eq \r(2).
法二 原式=2eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,2)sin \f(π,12)-\f(\r(3),2)cs \f(π,12)))
=2eq \b\lc\(\rc\)(\a\vs4\al\c1(cs \f(π,3)sin \f(π,12)-sin \f(π,3)cs \f(π,12)))=-2sineq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,3)-\f(π,12)))=-2sin eq \f(π,4)=-eq \r(2).
(2)原式=eq \f(cs 10°-\r(3)sin 10°,sin 10°cs 10°)=eq \f(2\b\lc\(\rc\)(\a\vs4\al\c1(\f(1,2)cs 10°-\f(\r(3),2)sin 10°)),sin 10°cs 10°)
=eq \f(4(sin 30°cs 10°-cs 30°sin 10°),2sin 10°cs 10°)=eq \f(4sin(30°-10°),sin 20°)=4.
感悟提升 三角函数公式活用技巧
(1)逆用公式应准确找出所给式子与公式的异同,创造条件逆用公式.
(2)tan αtan β,tan α+tan β(或tan α-tan β),tan(α+β)(或tan(α-β))三者中可以知二求一.应注重公式的逆用和变形使用.
考向二 三角函数式的化简
例3 (1)化简:eq \f(2cs4x-2cs2x+\f(1,2),2tan\b\lc\(\rc\)(\a\vs4\al\c1(\f(π,4)-x))sin2\b\lc\(\rc\)(\a\vs4\al\c1(\f(π,4)+x)))=________.
答案 eq \f(1,2)cs 2x
解析 原式=eq \f(\f(1,2)(4cs4x-4cs2x+1),2·\f(sin\b\lc\(\rc\)(\a\vs4\al\c1(\f(π,4)-x)),cs\b\lc\(\rc\)(\a\vs4\al\c1(\f(π,4)-x)))·cs2\b\lc\(\rc\)(\a\vs4\al\c1(\f(π,4)-x)))
=eq \f((2cs2x-1)2,4sin\b\lc\(\rc\)(\a\vs4\al\c1(\f(π,4)-x))cs\b\lc\(\rc\)(\a\vs4\al\c1(\f(π,4)-x)))=eq \f(cs22x,2sin\b\lc\(\rc\)(\a\vs4\al\c1(\f(π,2)-2x)))=eq \f(cs22x,2cs 2x)=eq \f(1,2)cs 2x.
(2)化简:(eq \f(1,tan \f(α,2))-tan eq \f(α,2))·eq \b\lc\(\rc\)(\a\vs4\al\c1(1+tan α·tan \f(α,2)))=________.
答案 eq \f(2,sin α)
解析 (eq \f(1,tan \f(α,2))-tan eq \f(α,2))·(1+tan α·tan eq \f(α,2))=(eq \f(cs \f(α,2),sin \f(α,2))-eq \f(sin \f(α,2),cs \f(α,2)))·(1+eq \f(sin α,cs α)·eq \f(sin\f(α,2),cs\f(α,2)))
=eq \f(cs2\f(α,2)-sin2\f(α,2),sin\f(α,2)cs\f(α,2))·eq \f(cs αcs\f(α,2)+sin αsin \f(α,2),cs αcs\f(α,2))=eq \f(2cs α,sin α)·eq \f(cs\f(α,2),cs αcs\f(α,2))=eq \f(2,sin α).
感悟提升 1.三角函数式的化简要遵循“三看”原则:一看角,二看名,三看式子结构与特征.
2.三角函数式的化简要注意观察条件中角之间的联系(和、差、倍、互余、互补等),寻找式子和三角函数公式之间的共同点.
考向三 三角函数求值问题
角度1 给角求值
例4 (1)sin 40°(tan 10°-eq \r(3))等于( )
A.2 B.-2
C.1 D.-1
答案 D
解析 sin 40°·(tan 10°-eq \r(3))=sin 40°·eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(sin 10°,cs 10°)-\r(3)))
=sin 40°·eq \f(sin 10°-\r(3)cs 10°,cs 10°)=sin 40°·eq \f(2\b\lc\(\rc\)(\a\vs4\al\c1(\f(1,2)sin 10°-\f(\r(3),2)cs 10°)),cs 10°)
=sin 40°·eq \f(2(cs 60°·sin 10°-sin 60°·cs 10°),cs 10°)=sin 40°·eq \f(2sin(10°-60°),cs 10°)
=sin 40°·eq \f(-2sin 50°,cs 10°)=eq \f(-2sin 40°·cs 40°,cs 10°)=eq \f(-sin 80°,cs 10°)=-1.
(2)cs 20°·cs 40°·cs 100°=________.
答案 -eq \f(1,8)
解析 cs 20°·cs 40°·cs 100°=-cs 20°·cs 40°·cs 80°
=-eq \f(sin 20°·cs 20°·cs 40°·cs 80°,sin 20°)=-eq \f(\f(1,2)sin 40°·cs 40°·cs 80°,sin 20°)
=-eq \f(\f(1,4)sin 80°·cs 80°,sin 20°)=-eq \f(\f(1,8)sin 160°,sin 20°)=-eq \f(\f(1,8)sin 20°,sin 20°)=-eq \f(1,8).
角度2 给值求值
例5 (1)(2023·安徽名校联考)已知cseq \b\lc\(\rc\)(\a\vs4\al\c1(α+\f(π,6)))=eq \f(3,4),则sineq \b\lc\(\rc\)(\a\vs4\al\c1(2α+\f(5π,6)))=( )
A.-eq \f(1,8) B.eq \f(1,8)
C.-eq \f(1,4) D.eq \f(1,4)
答案 B
解析 因为cseq \b\lc\(\rc\)(\a\vs4\al\c1(α+\f(π,6)))=eq \f(3,4),
所以sineq \b\lc\(\rc\)(\a\vs4\al\c1(2α+\f(5π,6)))=sineq \b\lc\[\rc\](\a\vs4\al\c1(\f(π,2)+\b\lc\(\rc\)(\a\vs4\al\c1(2α+\f(π,3)))))=cseq \b\lc\(\rc\)(\a\vs4\al\c1(2α+\f(π,3)))=2cs2eq \b\lc\(\rc\)(\a\vs4\al\c1(α+\f(π,6)))-1
=2×eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(3,4)))eq \s\up12(2)-1=eq \f(1,8).故选B.
(2)(2023·铁岭质检)已知eq \f(1,cs θ)+tan θ=2,则tan eq \f(θ,2)的值为( )
A.3 B.eq \f(1,3)或-1
C.eq \f(1,2) D.eq \f(1,3)
答案 D
解析 由eq \f(1,cs θ)+tan θ=eq \f(cs2\f(θ,2)+sin2\f(θ,2),cs2\f(θ,2)-sin2\f(θ,2))+eq \f(2tan \f(θ,2),1-tan2\f(θ,2))=eq \f(1+tan2\f(θ,2),1-tan2\f(θ,2))+eq \f(2tan \f(θ,2),1-tan2\f(θ,2))=2,
整理得3tan2eq \f(θ,2)+2tan eq \f(θ,2)-1=0,
解得tan eq \f(θ,2)=eq \f(1,3)或tan eq \f(θ,2)=-1.
因为cs θ≠0,所以θ≠eq \f(π,2)+kπ,k∈Z,
所以eq \f(θ,2)≠eq \f(π,4)+eq \f(kπ,2),k∈Z,
所以tan eq \f(θ,2)≠-1,故tan eq \f(θ,2)=eq \f(1,3).故选D.
角度3 给值求角
例6 已知α,β均为锐角,cs α=eq \f(2\r(7),7),sin β=eq \f(3\r(3),14),则cs 2α=________
2α-β=________.
答案 eq \f(1,7) eq \f(π,3)
解析 因为cs α=eq \f(2\r(7),7),
所以cs 2α=2cs2α-1=eq \f(1,7).
又因为α,β均为锐角,sin β=eq \f(3\r(3),14),
所以sin α=eq \f(\r(21),7),cs β=eq \f(13,14),
因此sin 2α=2sin αcs α=eq \f(4\r(3),7),
所以sin(2α-β)=sin 2αcs β-cs 2αsin β=eq \f(4\r(3),7)×eq \f(13,14)-eq \f(1,7)×eq \f(3\r(3),14)=eq \f(\r(3),2).
因为α为锐角,所以0<2α<π.
又cs 2α>0,所以0<2α<eq \f(π,2),
又β为锐角,所以-eq \f(π,2)<2α-β<eq \f(π,2),
又sin(2α-β)=eq \f(\r(3),2),所以2α-β=eq \f(π,3).
感悟提升 1.给值(角)求值问题求解的关键在于“变角”,使其角相同或具有某种关系,借助角之间的联系寻找转化方法.
2.给值(角)求值问题的一般步骤
(1)化简条件式子或待求式子;
(2)观察条件与所求之间的联系,从函数名称及角入手;
(3)将已知条件代入所求式子,化简求值.
考向四 三角恒等变换的应用
例7 设函数f(x)=sin x+cs x(x∈R).
(1)求函数y=eq \b\lc\[\rc\](\a\vs4\al\c1(f\b\lc\(\rc\)(\a\vs4\al\c1(x+\f(π,2)))))eq \s\up12(2)的最小正周期;
(2)求函数y=f(x)feq \b\lc\(\rc\)(\a\vs4\al\c1(x-\f(π,4)))在eq \b\lc\[\rc\](\a\vs4\al\c1(0,\f(π,2)))上的最大值.
解 (1)因为f(x)=sin x+cs x,
所以feq \b\lc\(\rc\)(\a\vs4\al\c1(x+\f(π,2)))=sineq \b\lc\(\rc\)(\a\vs4\al\c1(x+\f(π,2)))+cseq \b\lc\(\rc\)(\a\vs4\al\c1(x+\f(π,2)))=cs x-sin x,
所以y=eq \b\lc\[\rc\](\a\vs4\al\c1(f\b\lc\(\rc\)(\a\vs4\al\c1(x+\f(π,2)))))eq \s\up12(2)=(cs x-sin x)2=1-sin 2x.
所以函数y=eq \b\lc\[\rc\](\a\vs4\al\c1(f\b\lc\(\rc\)(\a\vs4\al\c1(x+\f(π,2)))))eq \s\up12(2)的最小正周期T=eq \f(2π,2)=π.
(2)feq \b\lc\(\rc\)(\a\vs4\al\c1(x-\f(π,4)))=sineq \b\lc\(\rc\)(\a\vs4\al\c1(x-\f(π,4)))+cseq \b\lc\(\rc\)(\a\vs4\al\c1(x-\f(π,4)))=eq \r(2)sin x,
所以y=f(x)feq \b\lc\(\rc\)(\a\vs4\al\c1(x-\f(π,4)))=eq \r(2)sin xeq \b\lc\(\rc\)(\a\vs4\al\c1(sin x+cs x))
=eq \r(2)(sin xcs x+sin2x)=eq \r(2)eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,2)sin 2x-\f(1,2)cs 2x+\f(1,2)))=sineq \b\lc\(\rc\)(\a\vs4\al\c1(2x-\f(π,4)))+eq \f(\r(2),2).
当x∈eq \b\lc\[\rc\](\a\vs4\al\c1(0,\f(π,2)))时,2x-eq \f(π,4)∈eq \b\lc\[\rc\](\a\vs4\al\c1(-\f(π,4),\f(3π,4))),
所以当2x-eq \f(π,4)=eq \f(π,2),即x=eq \f(3π,8)时,
函数y=f(x)feq \b\lc\(\rc\)(\a\vs4\al\c1(x-\f(π,4)))在eq \b\lc\[\rc\](\a\vs4\al\c1(0,\f(π,2)))上取得最大值,且ymax=1+eq \f(\r(2),2).
感悟提升 三角恒等变换的综合应用主要是将三角变换与三角函数的性质相结合,通过变换把函数化为f(x)=Asin(ωx+φ)+b的形式再研究其性质,解题时注意观察角、函数名、结构等特征,注意利用整体思想解决相关问题.
考向五 函数y=Asin(ωx+φ)的图象及变换
例8已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,-eq \f(π,2)<φ
(2)作出f(x)在[0,π]上的图象(要列表);
(3)函数y=f(x)的图象可由函数y=sin x的图象经过怎样的变换得到?
解 (1)因为函数f(x)的最小正周期是π,
所以ω=2.
又因为当x=eq \f(π,6)时,f(x)取得最大值2,所以A=2,
同时2×eq \f(π,6)+φ=2kπ+eq \f(π,2),k∈Z,
φ=2kπ+eq \f(π,6),k∈Z,
因为-eq \f(π,2)<φ
(2)因为x∈[0,π],
所以2x+eq \f(π,6)∈eq \b\lc\[\rc\](\a\vs4\al\c1(\f(π,6),\f(13π,6))).
列表如下:
描点、连线得图象:
(3)将y=sin x的图象上的所有点向左平移eq \f(π,6)个单位长度,得到函数y=sineq \b\lc\(\rc\)(\a\vs4\al\c1(x+\f(π,6)))的图象,再将y=sineq \b\lc\(\rc\)(\a\vs4\al\c1(x+\f(π,6)))的图象上所有点的横坐标缩短到原来的eq \f(1,2)(纵坐标不变),得到函数y=sineq \b\lc\(\rc\)(\a\vs4\al\c1(2x+\f(π,6)))的图象,再将y=sineq \b\lc\(\rc\)(\a\vs4\al\c1(2x+\f(π,6)))上所有点的纵坐标伸长2倍(横坐标不变),得到f(x)=2sineq \b\lc\(\rc\)(\a\vs4\al\c1(2x+\f(π,6)))的图象.
迁移 本例已知条件不变,第(3)问改为:函数y=f(x)的图象可由函数y=cs x的图象经过怎样的变换得到?
解 因为f(x)=2sineq \b\lc\(\rc\)(\a\vs4\al\c1(2x+\f(π,6)))=2cseq \b\lc\(\rc\)(\a\vs4\al\c1(2x+\f(π,6)-\f(π,2)))=2cseq \b\lc\(\rc\)(\a\vs4\al\c1(2x-\f(π,3))),
将y=cs x的图象上的所有点向右平移eq \f(π,3)个单位长度,得到函数y=cseq \b\lc\(\rc\)(\a\vs4\al\c1(x-\f(π,3)))的图象,再将y=cseq \b\lc\(\rc\)(\a\vs4\al\c1(x-\f(π,3)))的图象上所有点的横坐标缩短到原来的eq \f(1,2)(纵坐标不变),得到函数y=cseq \b\lc\(\rc\)(\a\vs4\al\c1(2x-\f(π,3)))的图象,再将y=cseq \b\lc\(\rc\)(\a\vs4\al\c1(2x-\f(π,3)))上所有点的纵坐标伸长2倍(横坐标不变),得到y=2cseq \b\lc\(\rc\)(\a\vs4\al\c1(2x-\f(π,3)))图象,
即为f(x)=2sineq \b\lc\(\rc\)(\a\vs4\al\c1(2x+\f(π,6)))的图象.
感悟提升 作函数y=Asin(ωx+φ)(A>0,ω>0)的图象常用如下两种方法:
(1)五点法作图,用“五点法”作y=Asin(ωx+φ)的简图,主要是通过变量代换,设z=ωx+φ,由z取0,eq \f(π,2),π,eq \f(3,2)π,2π来求出相应的x,通过列表,计算得出五点坐标,描点后得出图象;
(2)图象的变换法,由函数y=sin x的图象通过变换得到y=Asin(ωx+φ)的图象有两种途径:“先平移后伸缩”与“先伸缩后平移”.
基础题型训练
一、单选题
1.要得到函数的图象,只需将函数的图象上的所有点沿轴
A.向右平移1个单位长度B.向左平移3个单位长度
C.向左平移1个单位长度D.向右平移3个单位长度
【答案】C
【详解】分析:将函数的解析式化简和函数的解析式比较,即得解.
详解:=sin[3(x+1)-3],所以要得到函数的图象,只需将函数的图象上的所有点沿轴向左平移1个单位长度.
点睛:(1)本题主要考查三角函数图像的变换,意在考查学生对该知识的掌握水平.(2) 函数图像的平移变换:左加右减, 把函数向左平移个单位,得到函数的图像,把函数向右平移个单位,得到函数的图像.
2.把函数的图象向右平移个单位,得到的函数解析式为
A.B.
C.D.
【答案】C
【分析】根据三角函数的平移变换,即可得出答案.
【详解】函数的图象向右平移个单位,得到的函数
故选:C
【点睛】本题主要考查了由三角函数的平移变换求解析式,属于基础题.
3.已知函数的图象向右平移个单位长度,则平移后图象的对称中心为( )
A.B.
C.D.
【答案】A
【分析】根据三角函数的图象平移关系求出函数的解析式,结合函数的对称性进行求解即可.
【详解】将函数的图象向右平移个单位长度,
得,
由2xkπ,得x,k∈Z,即对称中心为(,0),k∈Z,
故选:A.
【点睛】本题主要考查三角函数的图象和性质,根据平移关系求出函数的解析式是解决本题的关键,属于基础题.
4.函数 在一个周期内的图像如图所示,则此函数的解析式为( )
A.B.
C.D.
【答案】B
【分析】根据图像易得与最小正周期,进而得到,再由最值点代入求得,即可得到结果.
【详解】由图知,,
把最值点代入,得,
,,
因此函数的解析式是.
故选:B.
5.将函数的图象上所有的点向右平行移动个单位长度,再把所得各点的横坐标伸长到原来的倍(纵坐标不变),所得图象的函数解析式是( )
A.B.
C.D.
【答案】C
【分析】根据三角函数图象变换的概念,先求出向右平移后的解析式,再求周期变换后的解析式.
【详解】将函数的图像上所有的点向右平行移动个单位长度,
得的图象,
再把所得各点的横坐标伸长到原来的2倍(纵坐标不变),
所得图像的函数解析式是.
故选:C.
6.已知函数,若在上有且只有3个零点,则的取值范围为( )
A.B.C.D.
【答案】A
【分析】,取得到,故,解得答案.
【详解】.
令,得,
函数的零点为…,,,,,,…
若在上有且只有3个零点,需满足,解得.
故选:A.
【点睛】本题考查了根据三角函数零点个数求参数范围,意在考查学生的计算能力和转化能力.
二、多选题
7.要得到函数的图象,只需将函数图象上所有点的坐标( )
A.向右平移个单位长度,再将横坐标缩短到原来的倍(纵坐标不变)
B.向左平移个单位长度,再将横坐标缩短到原来的倍(纵坐标不变)
C.横坐标缩短到原来的倍(纵坐标不变),再向左平移个单位长度
D.横坐标缩短到原来的倍(纵坐标不变),再向右平移个单位长度
【答案】BC
【分析】根据三角函数图象的伸缩平移变换即可得出结果.
【详解】函数的图象向左平移个长度单位,得,
再将横坐标缩短为原来的倍(纵坐标不变),得;
函数图象将横坐标缩短为原来的倍(纵坐标不变),得,
再向左平移个长度单位,得,即.
故选:BC
8.已知函数的部分图像如图所示,将的图像向右平移个单位后,得到函数的图像,若对于任意的,则值可以为( )
A.B.C.D.
【答案】CD
【分析】由于的图像过点,可得,结合,可得的值,由,解得,而,可得,再利用三角函数图像变换可得,从而由可得答案
【详解】解:由函数的图像可知,的图像过点,
所以,可得,
因为,所以,
因为的图像过点,
所以,解得,
所以,
因为,所以不妨设,则可得,
所以,
因为,
所以,
因为对于任意的,
所以,
所以,
所以,
当时,,
当时,,
故选:CD
三、填空题
9.在平面直角坐标系中,将曲线上每一点的横坐标保持不变,纵坐标变为原来的倍,所得新的曲线方程为__________.
【答案】
【分析】利用三角函数图象变换可得出新曲线的方程.
【详解】因为将曲线上每一点的横坐标保持不变,纵坐标变为原来的倍,
所得新的曲线方程为,
故答案为:.
10.若将函数的图象沿轴向右平移个单位后所得的图象与的图象关于轴对称,则的最小值为________________.
【答案】
【解析】由题意利用函数的图象变换规律,三角函数的图像的对称性,求得的最小值.
【详解】解:将函数的图象沿轴向右平移个单位长度,可得
的图象.
根据图象与的图象关于轴对称,可得,
,,即时,的最小值为.
故答案为:.
【点睛】本题主要考查函数的图象变换规律,正弦函数图像的对称性,属于基础题.
11.已知 ,若对任意 ,都有,则的最大值为________.
【答案】/0.5
【分析】运用整体法,根据正弦型函数的图像求解.
【详解】由题意, , ,又 , ,
由正弦函数 的单调性和周期性可知: ;
故答案为: .
12.下列四个命题:
①函数的值域是,则函数的值域为;
②把函数图像上的每一个点的横坐标伸长到原来的4倍,然后再向右平移个单位得到的函数解析式为;
③已知,则与共线的单位向量为;
④一条曲线和直线的公共点个数是m,则m的值不可能是1.
其中正确的有___________(写出所有正确命题的序号).
【答案】①④.
【分析】根据函数值域,平移和伸缩变换判断①②;根据单位向量概念求解③;④中利用图象变换画出函数图象,判断④正确.
【详解】对于①函数可以看作函数向左平移个单位值域不变是,则①正确;
对于②横坐标伸长到原来的倍,变为,再向右平移个单位,变为,则②错误;
对于③与共线的单位向量有两个,分别是和,则③错误;
对于④函数
作函数图象如下图所示:
可知与直线的公共点个数可为,不可能是,则④正确.
故答案为:①④
【点睛】本题考查命题的真假判断,考查函数性质,考查向量共线,属于中等题型.
四、解答题
13.函数的图像可以通过函数的图像经过怎样的平移得到?解释你的结论.
【答案】向左平移个单位,答案见解析
【分析】化为同名三角函数可得
【详解】因为故可以通过函数的图像向左平移个单位得到
14.已知函数(,,)的一段图像如下图所示,
(1)求函数的解析式;
(2)求函数的单调增区间;
【答案】(1)(2),.
【分析】(1)根据图象由最值求出A、周期求出,再代入特殊点求出即可求得函数解析式;(2)根据正弦函数的单调性列不等式求解即可.
【详解】(1)由题意知:,,,,
过点,,
,解得,
又,,则.
(2)令,,解得,
所以函数的单调增区间为,.
【点睛】本题考查正弦函数的图象与性质、根据图象确定正弦型函数的解析式,属于基础题.
15.已知函数(,,)的部分图像如图所示.
(1)求函数的解析式;
(2)求不等式的解集.
【答案】(1)
(2)
【分析】(1)首先根据函数图象得到,根据周期得到,再根据即可得到.
(2)根据题意得到,再解不等式即可.
【详解】(1)由题图知,
函数的周期,即,解得.
所以.
因为,所以,
又,所以.即.
(2)因为,即,
所以,.即,.
所以不等式的解集为.
16.设函数,其中,已知
(1)求;
(2)将函数的图像上的各点的横坐标伸长为原来的2倍(纵坐标不变),再将得到的图像向右平移个单位长度,得到函数的图像上,求在上的最小值.
【答案】(1)4(2)
【分析】(1)利用辅助角公式把化为,再利用得到满足的关系式,结合可求的值.
(2)利用周期变换得到,算出的范围后可得的最小值.
【详解】(1),
,,,
;
(2)由(1)知,
,
,
当时,即时,取最小值.
【点睛】本题考查形如的函数,可以利用降幂公式和辅助角公式将其化为的形式,再根据复合函数的讨论方法求该函数的单调区间、对称轴方程和对称中心等,属于中档题.
提升题型训练
一、单选题
1.要得到函数,的图像,只需把函数,的图像( )
A.向右平移个单位B.向右平移个单位
C.向左平移个单位D.向左平移个单位
【答案】A
【分析】由三角函数平移变换原则可直接得到结果.
【详解】对于A,向右平移个单位可得:,A正确;
对于B,向右平移个单位可得:,B错误;
对于C,向左平移个单位可得:,C错误;
对于D,向左平移个单位可得:,D错误.
故选:A.
2.将函数的图象向右平移个单位长度,得到函数的图象,若函数在上单调递增,则的最大值为( )
A.2B.C.D.4
【答案】B
【分析】根据余弦型函数的图象变换性质,结合余弦型函数的单调性进行求解即可.
【详解】因为函数的图象向右平移个单位长度,得到函数的图象,
所以,
当时,,
因为函数在上单调递增,
所以有,因此的最大值为,
故选:B
3.要得到函数的图象,只需将函数的图象( ).
A.向右平移个单位B.向左平移个单位C.向左平移个单位D.向右平移个单位
【答案】A
【分析】根据诱导公式,结合余弦函数的图象变换性质进行求解即可.
【详解】因为,
所以只需将函数的图象向右平移个单位,
故选:A
4.已知函数(其中),若对任意,存在,使得,则的取值范围为( )
A.B.C.D.
【答案】D
【解析】根据题意可知在的值域包含了上的值域,再分析列出不等式求解即可.
【详解】由题意可知,在的值域包含了上的值域,
故应当大于等于个周期才能使得值域包含了上的值域,
故.
故选:D
【点睛】本题主要考查了三角函数的图形变换与区间的不等式列式方法,需要考虑区间长度与周期的关系,属于中档题.
5.已知函数的最小正周期为,将其图象向右平移个单位后得函数的图象,则函数的图象
A.关于直线对称B.关于直线对称
C.关于点对称D.关于点对称
【答案】D
【详解】由题意得,故,
∴,
∴,
∴,
∴.
∵,,
∴选项A,B不正确.
又,
,
∴选项C,不正确,选项D正确.选D.
6.函数(其中,)的图象如图所示,为了得到的图象,则需将的图象( )
A.横坐标缩短到原来的,再向右平移个单位
B.横坐标缩短到原来的,再向右平移个单位
C.横坐标伸长到原来的倍,再向右平移个单位
D.横坐标伸长到原来的倍,再向右平移个单位
【答案】C
【分析】先根据图象的特点可求出,然后再根据周期变换与相位变换即可得出
【详解】由图可知,,所以,故,
故函数,
又函数图象经过点,故有,即,
所以(),
又,所以,
所以,
故将函数图象的横坐标伸长到原来的2倍得到的图象,然后再向右平移个单位即可得到的图象.
故选:C
二、多选题
7.下列说法错误的是( )
A.函数的最小正周期是
B.函数是周期为的奇函数
C.函数最小正周期为
D.若对,满足,,则函数周期为
【答案】BCD
【分析】A选项,使用进行求解最小正周期;B选项,利用定义判断出奇偶性;C选项,的最小正周期为;D选项,举出反例,即.
【详解】的最小正周期,故A选项说法正确;
,故为偶函数,故B说法错误;
函数最小正周期为,C说法错误;
若,此时,则为常数函数,任意数均为周期,D说法错误..
故选:BCD
8.已知函数相邻的最高点的距离为,则下列结论正确的是( )
A.函数的图象关于点中心对称
B.函数在区间上的值域为
C.将函数的图象上所有点的横坐标缩短为原来的,然后向左平移个单位得的图象
D.若,则
【答案】ACD
【分析】化简函数解析式根据周期求出,利用正弦型函数的对称性判断A,根据正弦型函数在区间上的值域判断B,由图象的伸缩与平移变换判断C,由三角恒等变换后求值判断D.
【详解】由题意,化简得,
由题意知周期,得,
所以,当时,,故A项正确;
当时,,故,故B项错误;
将函数的图象上所有点的横坐标缩短为原来的,得到,再向左平移个单位,可得,故C项正确;
由可得:,
于是,故D项正确.
故选:ACD
三、填空题
9.函数的初相是_________
【答案】
【分析】根据正弦型三角函数的物理意义判断初相即可.
【详解】解:因为初相是,即为.
故答案为:.
10.函数f(x)=Asin(ωx+φ)(A,ω,φ为常数,A>0,ω>0)的部分图象如图所示,则的值是_____.
【答案】
【详解】试题分析:观察图象可知:,,所以,则,所以函数为,又因为观察图象可知点相当于五点法中的,所以有:,解得:,所以函数,则.
考点:由正弦型函数图象求解析式.
11.将函数的图象向右平移个单位长度得到图像,则下列说法中正确的是______________(填序号).
①函数的最小正周期是; ②图像关于直线对称;
③函数在区间上单调递减; ④图像关于点对称;
【答案】①②④
【分析】根据三角函数的图象平移关系求出的解析式,结合函数的单调性,对称性分别进行判断即可.
【详解】由题意,将函数的图象向右平移个单位长度,可得,
对于A,函数的最小正周期为,故正确;
对于B,令,则为最大值,函数图象关于直线对称,故正确;
对于C中,,则,,则函数在区间上先减后增,故错误;
对于D中,令,则,图象关于点对称,故正确.
故答案为:①②④
【点睛】本题主要考查命题的真假判断,涉及三角函数的单调性,对称性,求出解析式是解决本题的关键,属于中档题.
12.已知函数,,则下列结论中正确的是______,
①若,则将图象向左平移个单位长度后得到的图象关于原点对称
②若,且的最小值为,则
③若在上单调递增,则的取值范围为
④当时,在有且只有3个零点
【答案】①②④
【分析】应用辅助角公式化简函数式,根据图象平移写出解析式判断①;由题设得即可求判断②;根据正弦型函数的单调性求的范围判断③;令结合给定区间确定零点个数判断④.
【详解】函数,
①若,,将向左平移个单位长度得到,其图象关于原点对称,故正确;
②若,且的最小值为,则,解得,故正确;
③当时,,若在上单调递增,则,解得,故错误;
④当时,,令,解得,
因为,满足的零点有,所以在有且只有3个零点,故正确;
故答案为: ①②④.
四、解答题
13.函数的图像可以通过函数的图像经过怎样的平移得到?解释你的结论.
【答案】向左平移个单位,答案见解析
【分析】化为同名三角函数可得
【详解】因为故可以通过函数的图像向左平移个单位得到
14.已知函数的最小正周期为,且.
(1)求和的值.
(2)将函数的图象向右平移个单位长度(纵坐标不变),得到函数的图象,
①求函数的单调递增区间;
②求函数在上的最大值.
【答案】(1),;(2)①;②最大值为.
【分析】(1)根据正弦型函数的最小正周期公式,结合特殊角的三角函数值进行求解即可;
(2)根据正弦型函数图象的变换性质,得到的解析式.
①根据余弦型函数的单调性进行求解即可;
②根据余弦型函数的最值性质进行求解即可.
【详解】解:(1)的最小正周期为,
所以,
即.
又因为,
所以,因为,
所以.
(2)由(1)可知,
函数的图象向右平移个单位长度(纵坐标不变),
所以.
①由,
得函数的单调递增区间为.
②因为,
所以.
当,
即时,
函数取得最大值,最大值为.
15.已知函数.
(1)求函数的最大值和最小值,并求取得最大值和最小值时对应的的值;
(2)设方程在区间内有两个相异的实数根,求的值.
【答案】(1)最大值为2,此时,最小值为-2,此时;(2)或
【分析】(1)利用诱导公式和二倍角公式以及辅助角公式化简原式,并根据最大值和最小值的计算公式求解出取最大值、最小值时对应的;
(2)将方程解的个数转化为函数图象的交点个数,借助图象分析求解出的值,注意对称性的应用.
【详解】(1),
的最大值为2,取得最大值对应的的值,
的最小值为-2,取得最小值对应的值.
(2)因为,所以,
在内有相异的两个实数根与在内有两个不同的交点,
在同一坐标系中作出与图象如下图:
由图象可知:或,
令,所以,
又因为,所以内的对称轴有:,
当,函数的图象关于直线对称,;
当,函数的图象关于直线对称,,
综上:或.
【点睛】本题考查三角函数性质的应用,着重考查了数形结合思想分析问题,难度一般.
(1)函数的零点个数方程根的数目与的图象交点个数;
(2)求解正弦型函数取最值时的值、对称轴,以整体的角度思考问题,
令分别等于正弦函数取最值时的值、对称轴,求解出的的取值集合即为所求结果.
16.函数在一个周期内的图象如图所示,为图象的最高点,,为图象与轴的交点,为等边三角形.将函数的图象上各点的横坐标变为原来的倍后,再向右平移个单位,得到函数的图象.
(Ⅰ)求函数的解析式;
(Ⅱ)若不等式对任意恒成立,求实数的取值范围.
【答案】(Ⅰ)(Ⅱ)
【分析】(Ⅰ)利用等边三角形的性质,根据已知,可以求出函数的周期,利用正弦型函数的最小正周期公式求出,最后根据正弦型函数图象的变换性质求出的解析式;
(Ⅱ)根据函数的解析式,原不等式等价于在恒成立,利用换元法,构造二次函数,分类讨论进行求解即可.
【详解】(Ⅰ)点的纵坐标为,为等边三角形,所以三角形边长为2,
所以,解得,所以,
将函数的图象上各点的横坐标变为原来的倍后,得到,
再向右平移个单位,得到.
(Ⅱ),
所以,
原不等式等价于在恒成立.
令,,即在上恒成立.
设,对称轴,
当时,即时,,解得,所以;
当时,即时,,解得(舍);
当时,即时,,解得.
综上,实数的取值范围为.
【点睛】本题考查了正弦型函数的图象变换和性质,考查了利用换元法、构造法解决不等式恒成立问题,考查了数学运算能力.
x
-eq \f(φ,ω)
-eq \f(φ,ω)+eq \f(π,2ω)
eq \f(π-φ,ω)
eq \f(3π,2ω)-eq \f(φ,ω)
eq \f(2π-φ,ω)
ωx+φ
0
eq \f(π,2)
π
eq \f(3π,2)
2π
y=Asin (ωx+φ)
0
A
0
-A
0
y=Asin(ωx+φ)(A>0,ω>0),x∈[0,+∞)表示一个振动量时
振幅
周期
频率
相位
初相
A
T=eq \f(2π,ω)
f=eq \f(1,T)
=eq \f(ω,2π)
ωx+φ
φ
2x+eq \f(π,6)
eq \f(π,6)
eq \f(π,2)
π
eq \f(3π,2)
2π
eq \f(13π,6)
x
0
eq \f(π,6)
eq \f(5π,12)
eq \f(2π,3)
eq \f(11π,12)
π
f(x)
1
2
0
-2
0
1
高考数学一轮复习《考点•题型•技巧》精讲与精练高分突破系列(新高考专用)专题2.1函数及其表示(原卷版+解析): 这是一份高考数学一轮复习《考点•题型•技巧》精讲与精练高分突破系列(新高考专用)专题2.1函数及其表示(原卷版+解析),共42页。
高考数学一轮复习《考点•题型•技巧》精讲与精练高分突破系列(新高考专用)7.1不等式的性质(原卷版+解析): 这是一份高考数学一轮复习《考点•题型•技巧》精讲与精练高分突破系列(新高考专用)7.1不等式的性质(原卷版+解析),共28页。试卷主要包含了两个实数比较大小的方法,不等式的性质,1 不等式的性质等内容,欢迎下载使用。
高考数学一轮复习《考点•题型•技巧》精讲与精练高分突破系列(新高考专用)4.3三角函数的图象与性质(原卷版+解析): 这是一份高考数学一轮复习《考点•题型•技巧》精讲与精练高分突破系列(新高考专用)4.3三角函数的图象与性质(原卷版+解析),共37页。试卷主要包含了辅助角公式,二倍角的正弦、余弦、正切公式等内容,欢迎下载使用。












