高考数学一轮复习《考点•题型•技巧》精讲与精练高分突破6.2等差数列(原卷版+解析)

这是一份高考数学一轮复习《考点•题型•技巧》精讲与精练高分突破6.2等差数列(原卷版+解析)，共33页。试卷主要包含了等差数列的有关概念，等差数列的前n项和公式，在等差数列中，若，，则，《九章算术》“竹九节”问题等内容，欢迎下载使用。


知识点总结
1．等差数列的有关概念
2．等差数列的前n项和公式
典型例题分析
考向一 等差数列基本量的运算
1．已知等差数列{an}的各项均为正数，其前n项和为Sn，且满足a6＝17，S5＝a2a3，则a12＝( )
A．28 B．30
C．32 D．35
解析：选D 设公差为d且d>0，由a6＝17，S5＝a2a3，得eq \b\lc\{\rc\ (\a\vs4\al\c1(a1＋5d＝17，,5a1＋10d＝a1＋da1＋2d，,d>0))⇒eq \b\lc\{\rc\ (\a\vs4\al\c1(a1＝2，,d＝3，))故a12＝a1＋11d＝2＋33＝35.
2．(2022·全国乙卷)记Sn为等差数列{an}的前n项和．若2S3＝3S2＋6，则公差d＝__________.
解析：因为2S3＝3S2＋6，所以2(a1＋a2＋a3)＝3(a1＋a2)＋6，化简得3d＝6，得d＝2.
答案：2
方法总结
解答等差数列运算问题的通法
(1)等差数列运算问题的一般求法是设出首项a1和公差d，然后由通项公式或前n项和公式转化为方程(组)求解．
(2)等差数列的通项公式及前n项和公式，共涉及a1，an，d，n，Sn五个量，知其中三个就能求另外两个，体现了解方程的思想．
考向二 等差数列的判定或证明
[典例] 在数列{an}中，Sn＋1＝4an＋2，a1＝1.
(1)设cn＝eq \f(an,2n)，求证数列{cn}是等差数列；
(2)求数列{an}的通项公式．
[解] (1)证明：在数列{an}中，∀n∈N*，Sn＋1＝4an＋2，则当n≥2时，有Sn＝4an－1＋2，
两式相减得an＋1＝4an－4an－1，而cn＝eq \f(an,2n)，即an＝2ncn，则有2n＋1cn＋1＝4×2ncn－4×2n－1cn－1，
整理得cn＋1＝2cn－cn－1，即cn＋1＋cn－1＝2cn，
所以数列{cn}是等差数列．
(2)由Sn＋1＝4an＋2得a1＋a2＝4a1＋2，而a1＝1，则a2＝5，c1＝eq \f(a1,2)＝eq \f(1,2)，c2＝eq \f(a2,22)＝eq \f(5,4)，
因此，等差数列{cn}的公差d＝eq \f(5,4)－eq \f(1,2)＝eq \f(3,4)，即{cn}是以eq \f(1,2)为首项，eq \f(3,4)为公差的等差数列，则cn＝eq \f(1,2)＋eq \f(3,4)(n－1)＝eq \f(3,4)n－eq \f(1,4)，即eq \f(an,2n)＝eq \f(3n－1,4)，于是得an＝(3n－1)·2n－2，
所以数列{an}的通项公式an＝(3n－1)·2n－2.
[方法技巧] 等差数列的判定与证明方法
考向三 等差数列的性质
角度1 等差数列的性质
[例1] (1)已知等差数列{an}的前n项和为Sn，若S10＝10，S20＝60，则S40等于( )
A．110 B．150 C．210 D．280
(2)我国古代数学著作《九章算术》有如下问题：“今有金箠，长五尺．斩本一尺，重四斤．斩末一尺，重二斤．问次一尺各重几何？”意思是：“现有一根金杖，长5尺，一头粗，一头细．在粗的一端截下1尺，重4斤，在细的一端截下1尺，重2斤．问依次每一尺各重多少斤？”假定该金杖被截成长度相等的若干段时，其质量从大到小构成等差数列．若将该金杖截成长度相等的20段，则中间两段的质量和为________斤．
(3)已知数列{an}，{bn}都是等差数列，Sn，Tn分别是它们的前n项和，并且eq \f(Sn,Tn)＝eq \f(7n＋3,3n＋8)，则eq \f(a7,b7)＝________.
[解析] (1)因为等差数列{an}的前n项和为Sn，所以S10，S20－S10，S30－S20，S40－S30也成等差数列．故(S30－S20)＋S10＝2(S20－S10)，所以S30＝150.又因为(S20－S10)＋(S40－S30)＝2(S30－S20)，所以S40＝280.
(2)设该若干段的质量从大到小构成等差数列{an}，由题意得，每4段为1尺，即a1＋a2＋a3＋a4＝4，a20＋a19＋a18＋a17＝2，两式相加得4(a1＋a20)＝6，则a10＋a11＝a1＋a20＝eq \f(3,2).
(3)因为{an}，{bn}为等差数列，所以eq \f(a7,b7)＝eq \f(2a7,2b7)＝eq \f(a1＋a13,b1＋b13)＝eq \f(\f(13a1＋a13,2),\f(13b1＋b13,2))＝eq \f(S13,T13)，又eq \f(Sn,Tn)＝eq \f(7n＋3,3n＋8)，
所以eq \f(a7,b7)＝eq \f(S13,T13)＝eq \f(7×13＋3,3×13＋8)＝eq \f(94,47)＝2.
[答案] (1)D (2)eq \f(3,2) (3)2
[方法技巧]
(1)运用等差数列的有关性质和结论可以提升解题效率．
(2)应用性质解题时，注意性质成立的前提条件．
(3)要注意等差数列通项公式及前n项和公式的灵活应用，如an＝am＋(n－m)d，d＝eq \f(an－am,n－m)，S2n－1＝(2n－1)an，Sn＝eq \f(na1＋an,2)＝eq \f(na2＋an－1,2)(n，m∈N*)等．
角度2 等差数列前n项和的最值
[例2] (多选)记等差数列{an}的前n项和为Sn.若a2＝10，S5＝S2，则( )
A．S3＝S4 B．a6＝10
C．Sn的最大值为30 D．an的最大值为15
[解析] 设等差数列的公差为d，则由题可得eq \b\lc\{\rc\ (\a\vs4\al\c1(a1＋d＝10，,5a1＋10d＝2a1＋d，))解得eq \b\lc\{\rc\ (\a\vs4\al\c1(a1＝15，,d＝－5，))∴an＝15＋(n－1)×(－5)＝20－5n，Sn＝eq \f(n15＋20－5n,2)＝eq \f(35n－5n2,2)，∴a4＝0，S3＝S4，故A正确；a6＝－10，故B错误；当n＝3或n＝4时，Sn取得最大值为30，故C正确；由于d<0，∴an的最大值为a1＝15，故D正确．
[答案] ACD
[方法技巧]
求等差数列前n项和Sn最值的方法
(1)函数法：利用等差数列前n项和的函数表达式Sn＝an2＋bn(a≠0)，通过配方或借助图象求二次函数最值的方法求解．
(2)邻项变号法：①若a1＞0，d＜0，则满足eq \b\lc\{\rc\ (\a\vs4\al\c1(am≥0，,am＋1≤0))的项数m使得Sn取得最大值Sm；
②若a1＜0，d＞0，则满足eq \b\lc\{\rc\ (\a\vs4\al\c1(am≤0，,am＋1≥0))的项数m使得Sn取得最小值Sm.
基础题型训练
一、单选题
1．观察下面的数表：若第n行的各数之和为231，则（ ）
A．15B．18C．20D．21
2．两等差数列{an}、{bn}的前n项和的比，则的值是
A．B．C．D．
3．设等差数列的前项和为，若，则当取最小值时，的值为（ ）
A．B．C．D．
4．在等差数列中，若，，则（ ）
A．B．C．D．
5．已知是各项均为正数的等差数列，且，则的最大值为（ ）
A．10B．20C．25D．50
6．数列的前项和为，若点在函数的图象上，则（ ）
A．2021B．4041C．4042D．4043
二、多选题
7．若为等差数列，，则下列说法正确的是（ ）
A．
B．是数列中的项
C．数列单调递减
D．数列前7项和最大
8．已知关于x的方程的四个根是公差为2的等差数列的前四项，为数列的前n项和，则（ ）
A．B．
C．D．
三、填空题
9．《九章算术》“竹九节”问题：现有一根节的竹子，自上而下各节的容积成等差数列，上面节的容积共升，下面节的容积共升，则第节的容积为__________升．
10．已知等差数列的前项和有最小值，且，则使得成立的的最小值是________．
11．已知公差不为零的等差数列的前项和为，若，则__________．
12．已知数列中，，则___________．
四、解答题
13．已知等差数列中，=1，，求数列的通项公式
14．已知数列满足﹒
(1)求证数列是等差数列；
(2)求的通项公式；
(3)试判断是否为数列中的项，并说明理由﹒
15．在等差数列中，，.
（1）求的通项公式；
（2）求的表达式.
16．已知在公比为2的等比数列中，成等差数列．
（1）求数列的通项公式；
（2）设求数列的前项和．
提升题型训练
一、单选题
1．在等差数列中，若，，则（ ）
A．38B．39C．40D．41
2．已知直线y＝25－3x，点(n，an)在该直线上，则a3＋a5＝（ ）
A．24B．25C．26D．27
3．北京天坛圜丘坛的地面由石板铺成，最中间的是圆形的天心石，围绕天心石的是扇环形的石板，从内到外各圈的石板数组成等差数列，它的前n项和为，且，，则（ ）
A．2079B．2059C．2022D．1890
4．已知等差数列的前项和为，若，，下列为真命题的序号为（ ）
①；②；③；④．
A．①②B．②③C．②④D．③④
5．孙子定理是中国古代求解一次同余式组的方法，是数论中一个重要定理，最早可见于中国南北朝时期的数学著作《孙子算经》，年英国来华传教士伟烈亚力将其问题的解法传至欧洲，年英国数学家马西森指出此法符合年由高斯得出的关于同余式解法的一般性定理，因而西方称之为“中国剩余定理”．这个定理讲的是一个关于整除的问题，现有这样一个整除问题：将至这个整数中能被除余且被除余的数按由小到大的顺序排成一列构成一数列，则此数列的项数是（ ）
A．B．C．D．
6．在中插入个数，使它们和组成等差数列，则（ ）
A．B．
C．D．
二、多选题
7．关于等差数列，有下列四个命题，正确的是（ ）
A．若数列中有两项是有理数，则其余各项都是有理数
B．等差数列的通项公式是关于项数n的一次函数
C．若数列是等差数列，则数列（k为常数）也是等差数列
D．若数列是等差数列，则数列也是等差数列
8．已知数列满足：，，，则下列说法正确的有（ ）
A．数列是等差数列B．
C．D．
三、填空题
9．在等差数列中，，，则________.
10．已知公差不为零的等差数列的前项和为，若，则__________．
11．已知等差数列{an}的前n项和为Sn，且，则a3+a6＝______
12．已知等差数列{an}的前n项和为Sn，且a2＝4，S5＝30，则数列{}的前n项和为_____．
四、解答题
13．已知数列的前n项和为，，，且.求证：数列是等差数列；
14．已知数列的前项和为.
(1)求数列的通项公式；
(2)求证：数列是等差数列.
15．已知等差数列，，公差，是数列的前项和，数列满足，，，是数列的前n项和.
(1)求数列，的通项公式；
(2)求证：.
16．设等差数列的前n项和为，已知，且是与的等差中项．
(1)求的值；
(2)若集合中最小的元素为6，求实数t的取值范围．
6.2 等差数列
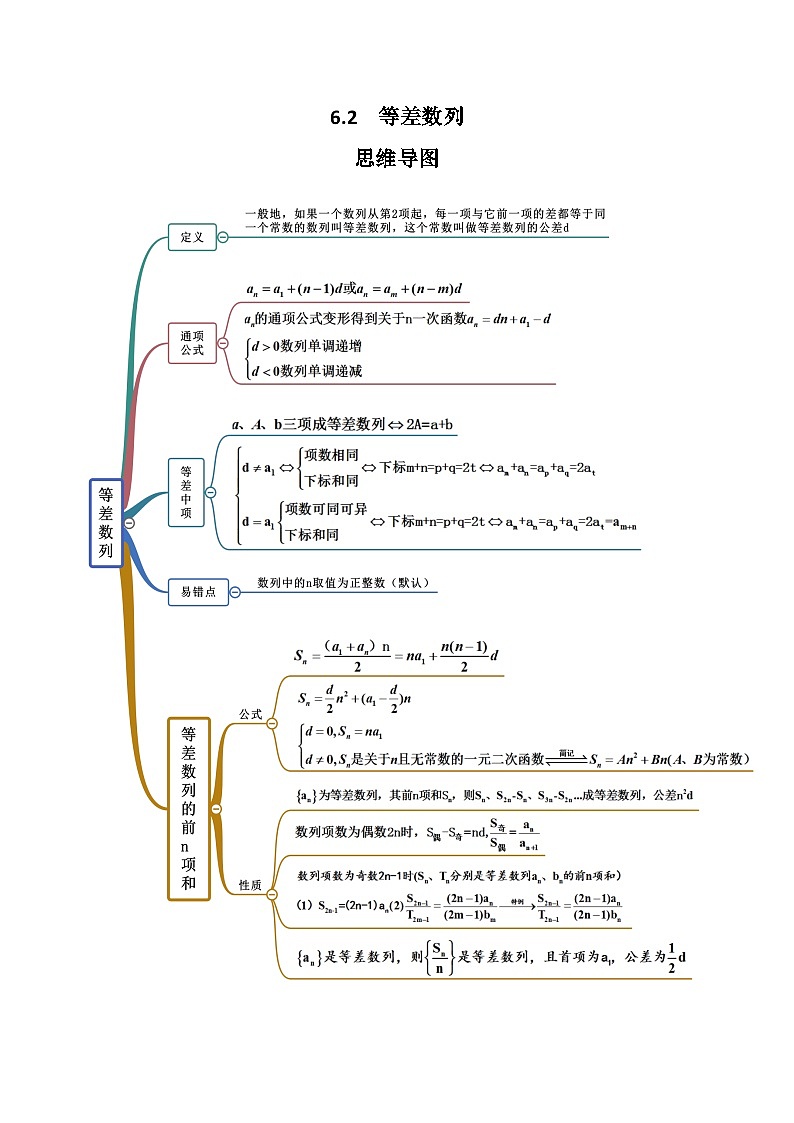
思维导图
知识点总结
1．等差数列的有关概念
2．等差数列的前n项和公式
典型例题分析
考向一 等差数列基本量的运算
1．已知等差数列{an}的各项均为正数，其前n项和为Sn，且满足a6＝17，S5＝a2a3，则a12＝( )
A．28 B．30
C．32 D．35
解析：选D 设公差为d且d>0，由a6＝17，S5＝a2a3，得eq \b\lc\{\rc\ (\a\vs4\al\c1(a1＋5d＝17，,5a1＋10d＝a1＋da1＋2d，,d>0))⇒eq \b\lc\{\rc\ (\a\vs4\al\c1(a1＝2，,d＝3，))故a12＝a1＋11d＝2＋33＝35.
2．(2022·全国乙卷)记Sn为等差数列{an}的前n项和．若2S3＝3S2＋6，则公差d＝__________.
解析：因为2S3＝3S2＋6，所以2(a1＋a2＋a3)＝3(a1＋a2)＋6，化简得3d＝6，得d＝2.
答案：2
方法总结
解答等差数列运算问题的通法
(1)等差数列运算问题的一般求法是设出首项a1和公差d，然后由通项公式或前n项和公式转化为方程(组)求解．
(2)等差数列的通项公式及前n项和公式，共涉及a1，an，d，n，Sn五个量，知其中三个就能求另外两个，体现了解方程的思想．
考向二 等差数列的判定或证明
[典例] 在数列{an}中，Sn＋1＝4an＋2，a1＝1.
(1)设cn＝eq \f(an,2n)，求证数列{cn}是等差数列；
(2)求数列{an}的通项公式．
[解] (1)证明：在数列{an}中，∀n∈N*，Sn＋1＝4an＋2，则当n≥2时，有Sn＝4an－1＋2，
两式相减得an＋1＝4an－4an－1，而cn＝eq \f(an,2n)，即an＝2ncn，则有2n＋1cn＋1＝4×2ncn－4×2n－1cn－1，
整理得cn＋1＝2cn－cn－1，即cn＋1＋cn－1＝2cn，
所以数列{cn}是等差数列．
(2)由Sn＋1＝4an＋2得a1＋a2＝4a1＋2，而a1＝1，则a2＝5，c1＝eq \f(a1,2)＝eq \f(1,2)，c2＝eq \f(a2,22)＝eq \f(5,4)，
因此，等差数列{cn}的公差d＝eq \f(5,4)－eq \f(1,2)＝eq \f(3,4)，即{cn}是以eq \f(1,2)为首项，eq \f(3,4)为公差的等差数列，则cn＝eq \f(1,2)＋eq \f(3,4)(n－1)＝eq \f(3,4)n－eq \f(1,4)，即eq \f(an,2n)＝eq \f(3n－1,4)，于是得an＝(3n－1)·2n－2，
所以数列{an}的通项公式an＝(3n－1)·2n－2.
[方法技巧] 等差数列的判定与证明方法
考向三 等差数列的性质
角度1 等差数列的性质
[例1] (1)已知等差数列{an}的前n项和为Sn，若S10＝10，S20＝60，则S40等于( )
A．110 B．150 C．210 D．280
(2)我国古代数学著作《九章算术》有如下问题：“今有金箠，长五尺．斩本一尺，重四斤．斩末一尺，重二斤．问次一尺各重几何？”意思是：“现有一根金杖，长5尺，一头粗，一头细．在粗的一端截下1尺，重4斤，在细的一端截下1尺，重2斤．问依次每一尺各重多少斤？”假定该金杖被截成长度相等的若干段时，其质量从大到小构成等差数列．若将该金杖截成长度相等的20段，则中间两段的质量和为________斤．
(3)已知数列{an}，{bn}都是等差数列，Sn，Tn分别是它们的前n项和，并且eq \f(Sn,Tn)＝eq \f(7n＋3,3n＋8)，则eq \f(a7,b7)＝________.
[解析] (1)因为等差数列{an}的前n项和为Sn，所以S10，S20－S10，S30－S20，S40－S30也成等差数列．故(S30－S20)＋S10＝2(S20－S10)，所以S30＝150.又因为(S20－S10)＋(S40－S30)＝2(S30－S20)，所以S40＝280.
(2)设该若干段的质量从大到小构成等差数列{an}，由题意得，每4段为1尺，即a1＋a2＋a3＋a4＝4，a20＋a19＋a18＋a17＝2，两式相加得4(a1＋a20)＝6，则a10＋a11＝a1＋a20＝eq \f(3,2).
(3)因为{an}，{bn}为等差数列，所以eq \f(a7,b7)＝eq \f(2a7,2b7)＝eq \f(a1＋a13,b1＋b13)＝eq \f(\f(13a1＋a13,2),\f(13b1＋b13,2))＝eq \f(S13,T13)，又eq \f(Sn,Tn)＝eq \f(7n＋3,3n＋8)，
所以eq \f(a7,b7)＝eq \f(S13,T13)＝eq \f(7×13＋3,3×13＋8)＝eq \f(94,47)＝2.
[答案] (1)D (2)eq \f(3,2) (3)2
[方法技巧]
(1)运用等差数列的有关性质和结论可以提升解题效率．
(2)应用性质解题时，注意性质成立的前提条件．
(3)要注意等差数列通项公式及前n项和公式的灵活应用，如an＝am＋(n－m)d，d＝eq \f(an－am,n－m)，S2n－1＝(2n－1)an，Sn＝eq \f(na1＋an,2)＝eq \f(na2＋an－1,2)(n，m∈N*)等．
角度2 等差数列前n项和的最值
[例2] (多选)记等差数列{an}的前n项和为Sn.若a2＝10，S5＝S2，则( )
A．S3＝S4 B．a6＝10
C．Sn的最大值为30 D．an的最大值为15
[解析] 设等差数列的公差为d，则由题可得eq \b\lc\{\rc\ (\a\vs4\al\c1(a1＋d＝10，,5a1＋10d＝2a1＋d，))解得eq \b\lc\{\rc\ (\a\vs4\al\c1(a1＝15，,d＝－5，))∴an＝15＋(n－1)×(－5)＝20－5n，Sn＝eq \f(n15＋20－5n,2)＝eq \f(35n－5n2,2)，∴a4＝0，S3＝S4，故A正确；a6＝－10，故B错误；当n＝3或n＝4时，Sn取得最大值为30，故C正确；由于d<0，∴an的最大值为a1＝15，故D正确．
[答案] ACD
[方法技巧]
求等差数列前n项和Sn最值的方法
(1)函数法：利用等差数列前n项和的函数表达式Sn＝an2＋bn(a≠0)，通过配方或借助图象求二次函数最值的方法求解．
(2)邻项变号法：①若a1＞0，d＜0，则满足eq \b\lc\{\rc\ (\a\vs4\al\c1(am≥0，,am＋1≤0))的项数m使得Sn取得最大值Sm；
②若a1＜0，d＞0，则满足eq \b\lc\{\rc\ (\a\vs4\al\c1(am≤0，,am＋1≥0))的项数m使得Sn取得最小值Sm.
基础题型训练
一、单选题
1．观察下面的数表：若第n行的各数之和为231，则（ ）
A．15B．18C．20D．21
【答案】C
【分析】观察数表的规律利用等差数列的前项和公式求解即可.
【详解】设第n行的各数之和为，
则,,…，，
令，即，解得或（舍去）
故选：C.
2．两等差数列{an}、{bn}的前n项和的比，则的值是
A．B．C．D．
【答案】D
【分析】依据等差数列角标和性质去求的值即可.
【详解】
故选：D.
3．设等差数列的前项和为，若，则当取最小值时，的值为（ ）
A．B．C．D．
【答案】B
【解析】根据等差数列的前项和以及等差数列的性质可得，，进而可得最小.
【详解】由等差数列前项和公式可得:
，所以，
，所以，故，
所以等差数列的前项为负数，从第项起为正，故前项的和最小，
所以的值为，
故选：B
【点睛】关键点点睛：本题的关键点是利用，得出，进而可得最小.
4．在等差数列中，若，，则（ ）
A．B．C．D．
【答案】C
【分析】利用等差数列性质，若，则及等差中项公式可求．
【详解】因为，由等差中项公式，得，
同理，得，
．
故选：C
5．已知是各项均为正数的等差数列，且，则的最大值为（ ）
A．10B．20C．25D．50
【答案】C
【分析】根据等差数列的性质，化简原式，得到，用基本不等式求最值.
【详解】∵，∴，
由已知，得，
∴，当且仅当时等号成立.
故选：C.
6．数列的前项和为，若点在函数的图象上，则（ ）
A．2021B．4041C．4042D．4043
【答案】D
【分析】根据点在函数的图象上，得到，再利用数列通项与前n项和的关系求解.
【详解】因为点在函数的图象上，
所以，
当时，，
当时，，
又适合上式，
所以，
所以，
故选：D
【点睛】方法点睛：1、数列的通项an与前n项和Sn的关系是，当n＝1时，a1若适合Sn－Sn－1，则n＝1的情况可并入n≥2时的通项an；当n＝1时，a1若不适合Sn－Sn－1，则用分段函数的形式表示．
二、多选题
7．若为等差数列，，则下列说法正确的是（ ）
A．
B．是数列中的项
C．数列单调递减
D．数列前7项和最大
【答案】ACD
【分析】由为等差数列，列方程组求得首项与公差，就可得到通项公式，然后对选项逐一判断即可.
【详解】因为数列为等差数列，且，则，解得，，故A选项正确，
由，得，故B错误，
因为，所以数列单调递减，故C正确，
由数列通项公式可知，前7项均为正数，，所以前7项和最大,故D正确.
故选：ACD
8．已知关于x的方程的四个根是公差为2的等差数列的前四项，为数列的前n项和，则（ ）
A．B．
C．D．
【答案】BCD
【分析】根据韦达定理可得，进而求得首项，即可得，即可判断选项A，C，D；由韦达定理可知代入即可判断D.
【详解】解：因为为等差数列，所以，
因为，可得，，，，
所以数列的通项公式为，
故，代入可得，，，
故选项A不正确，选项C，D正确；
根据韦达定理可得，，故选项B正确．
故选：BCD．
三、填空题
9．《九章算术》“竹九节”问题：现有一根节的竹子，自上而下各节的容积成等差数列，上面节的容积共升，下面节的容积共升，则第节的容积为__________升．
【答案】
【分析】设自上而下的竹子容量依次为，可得为等差数列，根据，，可得数列的通项公式及
【详解】设自上而下的竹子容量依次为，可得为等差数列，
则，解得，
故，，
故答案为：.
10．已知等差数列的前项和有最小值，且，则使得成立的的最小值是________．
【答案】22
【分析】根据等差数列的前项和有最小值，得到公差，再由，得到 ，利用等差数列的性质结合前n项和公式求解.
【详解】因为等差数列的前项和有最小值，
所以等差数列的公差，
又因为，
所以 ，
所以 ，
，
所以使得成立的的最小值是22，
故答案为：22
11．已知公差不为零的等差数列的前项和为，若，则__________．
【答案】
【分析】用公差和首项表示已知式，求得关系后再代入求值式计算．
【详解】设公差为，则，，
所以．
故答案为：．
12．已知数列中，，则___________．
【答案】
【详解】试题分析：由，即，即数列表示首项为，公差为的等差数列，所以数列的通项公式，则，令，即，即当时，则，当，则，所以
．
考点：等差数列求和问题．
四、解答题
13．已知等差数列中，=1，，求数列的通项公式
【答案】
【分析】设等差数列的公差为,进而结合已知条件列方程求解，进而得答案.
【详解】设等差数列的公差为，则
由得，解得
所以，
所以数列的通项公式为
14．已知数列满足﹒
(1)求证数列是等差数列；
(2)求的通项公式；
(3)试判断是否为数列中的项，并说明理由﹒
【答案】(1)见解析；
(2)；
(3)是，理由见解析﹒
【分析】(1)已知条件两边同时取倒数，构造等差数列求解；
(2)根据(1)中构造的等差数列即可求通项公式；
(3)令通项等于，解出n，如果n为正整数，则是该数列的项，否则不是﹒
【详解】（1）由题可得，
∴是以3为首项，3为公差的等差数列；
（2）由(1)得，，
∴；
（3）令，解得，故是为数列中的项﹒
15．在等差数列中，，.
（1）求的通项公式；
（2）求的表达式.
【答案】（1）；（2）.
【分析】（1）设公差为，根据通项公式得关于和的方程组，解方程组可得答案；
（2）按照和两种情况讨论去掉绝对值，转为等差数列的求和公式即可得到.
【详解】（1）设公差为，
则，解得，，
所以.
（2）由可得，
所以当时，，
当时，
.
所以.
【点睛】本题考查了求等差数列的通项公式，考查了等差数列的求和公式，解题关键是通过讨论去掉绝对值，属于中档题.
16．已知在公比为2的等比数列中，成等差数列．
（1）求数列的通项公式；
（2）设求数列的前项和．
【答案】（1）；（2）.
【分析】（1）利用等比数列的基本量代换，求出，套公式求出通项公式；
（2）分别分析出奇数项是以6为首项，10为公差的等差数列，偶数项是以2为首项，2为公比的等比数列，利用分组求和法求和即可.
【详解】解：（1）因为数列的公比q为2，
所以．
因为成等差数列，
所以，
解得，所以．
（2）由（1）可得
所以奇数项是以6为首项，10为公差的等差数列，偶数项是以2为首项，2为公比的等比数列，
所以
．
提升题型训练
一、单选题
1．在等差数列中，若，，则（ ）
A．38B．39C．40D．41
【答案】B
【分析】根据，求出，然后用公式计算即可.
【详解】在等数列中，，
所以，
解得，
所以，
故选：B.
2．已知直线y＝25－3x，点(n，an)在该直线上，则a3＋a5＝（ ）
A．24B．25C．26D．27
【答案】C
【分析】根据数列的通项公式计算即可得解.
【详解】由题意知an＝25－3n，
∴a3＋a5＝(25－3×3)＋(25－3×5)＝26．
故选：C
3．北京天坛圜丘坛的地面由石板铺成，最中间的是圆形的天心石，围绕天心石的是扇环形的石板，从内到外各圈的石板数组成等差数列，它的前n项和为，且，，则（ ）
A．2079B．2059C．2022D．1890
【答案】A
【分析】利用等差数列通项公式求基本量，再由等差数列前n项和公式求.
【详解】由题设，可得，
所以.
故选：A
4．已知等差数列的前项和为，若，，下列为真命题的序号为（ ）
①；②；③；④．
A．①②B．②③C．②④D．③④
【答案】B
【分析】由，，可得，即，，再根据等差数列的性质及基本量的运算可求解.
【详解】由，
可得，即，，
故可得等差数列的公差，选项③正确；
把已知的两式相加可得
整理可得
结合上面的判断可知
故有，，故选项②正确；
由于，，则，故选项①错误；
由公差 可得，结合等差数列的列的性质，
可得，从而可得，故，即选项④错误．
故选：B．
5．孙子定理是中国古代求解一次同余式组的方法，是数论中一个重要定理，最早可见于中国南北朝时期的数学著作《孙子算经》，年英国来华传教士伟烈亚力将其问题的解法传至欧洲，年英国数学家马西森指出此法符合年由高斯得出的关于同余式解法的一般性定理，因而西方称之为“中国剩余定理”．这个定理讲的是一个关于整除的问题，现有这样一个整除问题：将至这个整数中能被除余且被除余的数按由小到大的顺序排成一列构成一数列，则此数列的项数是（ ）
A．B．C．D．
【答案】D
【分析】列举出该数列的前几项，可知该数列为等差数列，求出等差数列的首项和公差，进而可得出数列的通项公式，然后求解满足不等式的正整数的个数，即可得解.
【详解】设所求数列为，该数列为、、、、，
所以，数列为等差数列，且首项为，公差为，
所以，，
解不等式，即，解得，
则满足的正整数的个数为，
因此，该数列共有项.
故选：D.
【点睛】本题考查数列项数的计算，求出数列的通项公式是解答的关键，考查计算能力，属于中等题.
6．在中插入个数，使它们和组成等差数列，则（ ）
A．B．
C．D．
【答案】B
【分析】根据等差数列的性质，利用倒序相加法求得所求表达式的值.
【详解】令，倒过来写，两式相加得，故，所以，故选B.
【点睛】本小题主要考查等差数列的性质，即，考查倒序相加法，属于基础题.
二、多选题
7．关于等差数列，有下列四个命题，正确的是（ ）
A．若数列中有两项是有理数，则其余各项都是有理数
B．等差数列的通项公式是关于项数n的一次函数
C．若数列是等差数列，则数列（k为常数）也是等差数列
D．若数列是等差数列，则数列也是等差数列
【答案】AC
【分析】根据等差数列的定义逐一验证即可.
【详解】选项A正确.当时，选项B不成立.
由等差数列的定义知选项C正确，证明如下：设的公差为d，则（常数），所以也是等差数列.
选项D错误,比如数列为：-2，-1，0，1，2，则数列为：4，1，0，1，4
故选：AC
8．已知数列满足：，，，则下列说法正确的有（ ）
A．数列是等差数列B．
C．D．
【答案】BC
【分析】A.利用等差中项判断；BC.根据，由数列的奇数项和偶数项构成等差数列判断；D.令判断.
【详解】因为，，，则，而，故A错误；
因为，所以数列的奇数项和偶数项构成等差数列，
当时，，
当时，，故BC正确；
因为，不满足，故D错误；
故选：BC
三、填空题
9．在等差数列中，，，则________.
【答案】
【分析】利用等差中项的性质得出，由此可得出的值.
【详解】由等差中项的性质得，.
故答案为：.
【点睛】本题考查了等差中项性质的应用，考查计算能力，属于基础题．
10．已知公差不为零的等差数列的前项和为，若，则__________．
【答案】
【分析】用公差和首项表示已知式，求得关系后再代入求值式计算．
【详解】设公差为，则，，
所以．
故答案为：．
11．已知等差数列{an}的前n项和为Sn，且，则a3+a6＝______
【答案】
【解析】由定积分的几何意义和微积分基本定理求得，再由等差数列的前项和公式与等差数列的性质求得结论．
【详解】解：令，则y≥0，两边平方得y2＝1﹣x2，即x2+y2＝1，
则函数在区间[﹣1，1]上的图象是圆x2+y2＝1的上半部分，
则，
则，
由于数列{an}为等差数列，则a3+a6＝a1+a8，
所以，因此，
故答案为：．
【点睛】本题考查微积分基本定理，定积分的几何意义，等差数列的前项和，等差数列的性质，解题时要选择恰当地公式计算．
12．已知等差数列{an}的前n项和为Sn，且a2＝4，S5＝30，则数列{}的前n项和为_____．
【答案】
【分析】依据等差数列通项及前n项和公式求得等差数列{an}的基本量，应用等差数列前n项和公式表示出，进而得到数列{}的通项，并利用裂项法求前n项和即可
【详解】根据等差数列通项及前n项和公式，知
解得
∴由等差数列前n项和公式：，
对于数列{}有
∴数列{}的前n项和
故答案为：
【点睛】本题考查了等差数列，根据已知量，结合等差数列的通项公式和前n项和公式列方程求基本量，进而得到其前n项和公式，根据新数列与等差数列前n项和的关系求得数列通项公式，结合裂项法得到新数列的前n项和公式
四、解答题
13．已知数列的前n项和为，，，且.求证：数列是等差数列；
【答案】证明见解析
【分析】由，得，又，根据等差数列的定义可证结论正确.
【详解】因为，
所以，即，
则．
又，，满足，
所以，
所以是公差为4的等差数列．
14．已知数列的前项和为.
(1)求数列的通项公式；
(2)求证：数列是等差数列.
【答案】(1)
(2)见解析
【分析】（1）由，即可求出数列的通项公式；
（2）由等差数列的定义证明即可；
【详解】（1）当时，，
当时，，
令，满足，所以.
（2）由（1）知，，
所以数列是以首项为，公差为等差数列.
15．已知等差数列，，公差，是数列的前项和，数列满足，，，是数列的前n项和.
(1)求数列，的通项公式；
(2)求证：.
【答案】(1)，；
(2)证明见解析.
【分析】（1）根据等差数列的通项公式，求和公式求解即可；
（2）由可得，由，可得 .
(1)
∵数列为等差数列，
，公差，∴，
∴.
∵，
∴.
(2)
证明：∵，
∴，不等式左边得证.
当时，；
当时，，
∴
.
综上，.
16．设等差数列的前n项和为，已知，且是与的等差中项．
(1)求的值；
(2)若集合中最小的元素为6，求实数t的取值范围．
【答案】(1)；
(2)
【分析】（1）利用题给条件列出关于的方程组，解之即可求得的值；
（2）利用题给条件列出关于实数t的不等式，解之即可求得实数t的取值范围．
【详解】（1）设等差数列的首项为，公差为d，
则，解之得，则
（2）由（1）得等差数列的首项为1，公差为2，则，
由集合中最小的元素为6，
可得满足不等式的最小正整数n为6，
则，解之得
则实数t的取值范围为
定义
如果一个数列从第2项起，每一项与它的前一项的差都等于 ，那么这个数列就叫做等差数列，即an＋1－an＝d(n∈N*，d为常数)
通项公式
设{an}是首项为a1，公差为d的等差数列，则通项公式an＝
等差中项
由三个数a，A，b组成的等差数列可以看成是最简单的等差数列．这时，A叫做a与b的等差中项．根据等差数列的定义可以知道，2A＝
已知条件
前n项和公式
a1，an，n
a1，d，n
定义法
如果一个数列{an}从第2项起，每一项与它的前一项的差等于同一个常数，那么可以判断数列{an}为等差数列
等差
中项法
如果一个数列{an}对任意的正整数n都满足2an＋1＝an＋an＋2，那么可以判断{an}为等差数列
通项
公式法
如果一个数列{an}的通项公式满足an＝pn＋q(p，q为常数)的形式，那么可以提出{an}是首项为p＋q，公差为p的等差数列，适用选择、填空题
前n项和
公式法
如果一个数列{an}的前n项和公式满足Sn＝An2＋Bn(A，B为常数)的形式，那么可以得出数列{an}是首项为A＋B，公差为2A的等差数列，适用选择、填空题
定义
如果一个数列从第2项起，每一项与它的前一项的差都等于同一个常数，那么这个数列就叫做等差数列，即an＋1－an＝d(n∈N*，d为常数)
通项公式
设{an}是首项为a1，公差为d的等差数列，则通项公式an＝a1＋(n－1)d
等差中项
由三个数a，A，b组成的等差数列可以看成是最简单的等差数列．这时，A叫做a与b的等差中项．根据等差数列的定义可以知道，2A＝a＋b
已知条件
前n项和公式
a1，an，n
Sn＝eq \f(na1＋an,2)
a1，d，n
Sn＝na1＋eq \f(nn－1,2)d
定义法
如果一个数列{an}从第2项起，每一项与它的前一项的差等于同一个常数，那么可以判断数列{an}为等差数列
等差
中项法
如果一个数列{an}对任意的正整数n都满足2an＋1＝an＋an＋2，那么可以判断{an}为等差数列
通项
公式法
如果一个数列{an}的通项公式满足an＝pn＋q(p，q为常数)的形式，那么可以提出{an}是首项为p＋q，公差为p的等差数列，适用选择、填空题
前n项和
公式法
如果一个数列{an}的前n项和公式满足Sn＝An2＋Bn(A，B为常数)的形式，那么可以得出数列{an}是首项为A＋B，公差为2A的等差数列，适用选择、填空题