2025高考数学一轮复习-7.1.2-全概率公式【课件】

这是一份2025高考数学一轮复习-7.1.2-全概率公式【课件】，共7页。

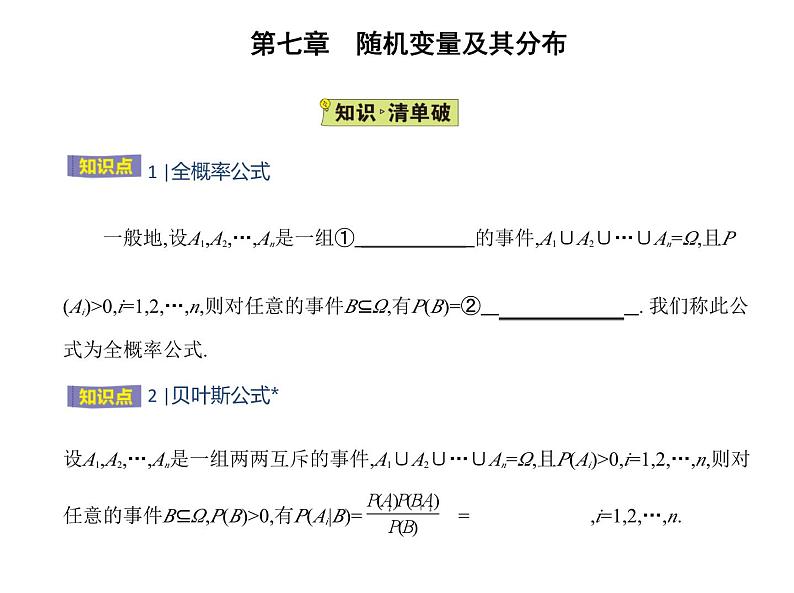
　　一般地,设A1,A2,…,An是一组①　两两互斥    的事件,A1∪A2∪…∪An=Ω,且P (Ai)>0,i=1,2,…,n,则对任意的事件B⊆Ω,有P(B)=②     P(Ai)P(B|Ai)    . 我们称此公 式为全概率公式.
设A1,A2,…,An是一组两两互斥的事件,A1∪A2∪…∪An=Ω,且P(Ai)>0,i=1,2,…,n,则对 任意的事件B⊆Ω,P(B)>0,有P(Ai|B)= = ,i=1,2,…,n. 
第七章　随机变量及其分布
 1.全概率公式中的A1,A2,…,An可以是任意一组随机事件.(    ✕　)2.全概率公式的应用即已知事件B的发生有各种可能的情形Ai(i=1,2,…,n),事件B发 生的可能性,就是各种可能情形Ai发生可能性的概率之和. (    ✕　)全概率公式的直观解释:已知事件B的发生有各种可能的情形Ai(i=1,2,…,n),事件B 发生的可能性,就是各种可能情形Ai发生的可能性与已知在Ai发生的条件下事件B 发生的可能性的乘积之和.3.全概率公式的主要作用是“由结果推测原因”.(    ✕　)
判断正误，正确的画“ √” ，错误的画“ ✕” .
全概率公式的主要作用是“由原因推测结果”.
1 |全概率公式及其应用
 　　全概率公式的意义在于,当直接计算事件B发生的概率P(B)较为困难时,可以先 找到样本空间Ω的一个划分Ω=A1∪A2∪…∪An,A1,A2,…,An两两互斥,将A1,A2,…,An看 成是导致B发生的一组原因,这样事件B就被分解成了n个部分,分别计算P(B|A1),P(B |A2),…,P(B|An),再利用全概率公式求解.运用全概率公式计算事件B发生的概率P(B)时,一般步骤如下:(1)先求划分后的每个小事件的概率,即P(Ai), i =1,2,…,n;(2)再求每个小事件发生的条件下,事件B发生的概率,即P(B|Ai), i =1,2,…,n;(3)最后利用全概率公式计算P(B),即P(B)=   
已知某超市的玻璃杯成箱出售,每箱20只,假设各箱含0,1,2只残次品的概率分别是 0.8,0.1,0.1,某顾客欲购一箱玻璃杯,在购买时,售货员随机取出一箱,顾客开箱随机查看4只,若无残次品,则买下该箱玻璃杯,否则退回,试求顾客买下该箱玻璃杯的概率.解析    记事件B为顾客买下该箱玻璃杯,事件Ai为取出的一箱中有i只残次品,i=0,1,2.则P(A0)=0.8,P(A1)=0.1,P(A2)=0.1,P(B|A0)=1,P(B|A1)= = ,P(B|A2)= = ,由全概率公式可得,P(B)=P(A0)P(B|A0)+P(A1)P(B|A1)+P(A2)P(B|A2)=0.8×1+0.1× +0.1× ≈0.94.
即顾客买下该箱玻璃杯的概率约为0.94.
2 |贝叶斯公式*及其应用
 　　贝叶斯公式是在条件概率的基础上寻找事件发生的原因,在运用贝叶斯公式 时,一般已知和未知条件如下:(1)A的多种情况中到底哪种情况发生是未知的,但是每种情况发生的概率已知,即P (Ai)已知;(2)事件B是已经发生的确定事实,且A的每种情况发生的条件下B发生的概率已知, 即P(B|Ai)已知;(3)P(B)未知,需要使用全概率公式计算得到;(4)求解的目标是用A的某种情况Ai的无条件概率求其在B发生的条件下的有条件 概率P(Ai|B).