专题16 导数及其应用小题综合（学生卷）- 十年（2015-2024）高考真题数学分项汇编（全国通用）

这是一份专题16 导数及其应用小题综合（学生卷）- 十年（2015-2024）高考真题数学分项汇编（全国通用），共9页。试卷主要包含了设函数等内容，欢迎下载使用。

考点01 导数的基本计算及其应用
1．（2020·全国·高考真题）设函数．若，则a= ．
2．（2018·天津·高考真题）已知函数f(x)=exlnx，为f(x)的导函数，则的值为 ．
3．（2016·天津·高考真题）已知函数为的导函数，则的值为 .
4．（2015·天津·高考真题）已知函数，其中为实数，为的导函数，若，则的值为 ．
考点02 求切线方程及其应用
1．（2024·全国甲卷·高考真题）设函数，则曲线在点处的切线与两坐标轴所围成的三角形的面积为（ ）
A．B．C．D．
2．（2023·全国甲卷·高考真题）曲线在点处的切线方程为（ ）
A．B．C．D．
3．（2022·全国新Ⅱ卷·高考真题）曲线过坐标原点的两条切线的方程为 ， ．
4．（2022·全国新Ⅰ卷·高考真题）若曲线有两条过坐标原点的切线，则a的取值范围是 ．
5．（2021·全国甲卷·高考真题）曲线在点处的切线方程为 ．
6．（2021·全国新Ⅱ卷·高考真题）已知函数，函数的图象在点和点的两条切线互相垂直，且分别交y轴于M，N两点，则取值范围是 ．
7．（2021·全国新Ⅰ卷·高考真题）若过点可以作曲线的两条切线，则（ ）
A．B．
C．D．
8．（2020·全国·高考真题）若直线l与曲线y=和x2+y2=都相切，则l的方程为（ ）
A．y=2x+1B．y=2x+C．y=x+1D．y=x+
9．（2020·全国·高考真题）函数的图像在点处的切线方程为（ ）
A．B．
C．D．
10．（2020·全国·高考真题）曲线的一条切线的斜率为2，则该切线的方程为 .
11．（2019·江苏·高考真题）在平面直角坐标系中，点A在曲线y=lnx上，且该曲线在点A处的切线经过点（-e，-1)(e为自然对数的底数），则点A的坐标是 .
12．（2019·全国·高考真题）已知曲线在点处的切线方程为，则
A．B．C．D．
13．（2019·天津·高考真题） 曲线在点处的切线方程为 .
14．（2019·全国·高考真题）曲线在点处的切线方程为 ．
15．（2019·全国·高考真题）曲线y=2sinx+csx在点(π，–1)处的切线方程为
A．B．
C．D．
16．（2018·全国·高考真题）设函数．若为奇函数，则曲线在点处的切线方程为( )
A．B．C．D．
17．（2018·全国·高考真题）曲线在点处的切线的斜率为，则 ．
18．（2018·全国·高考真题）曲线在点处的切线方程为 ．
19．（2018·全国·高考真题）曲线在点处的切线方程为 ．
20．（2017·全国·高考真题）曲线在点（1，2）处的切线方程为 ．
21．（2016·全国·高考真题）已知为偶函数，当 时，，则曲线在点处的切线方程是 .
22．（2016·全国·高考真题）已知为偶函数，当时，，则曲线在点处的切线方程是 ．
23．（2015·全国·高考真题）已知函数的图像在点的处的切线过点，则 .
24．（2015·陕西·高考真题）设曲线在点（0,1）处的切线与曲线上点处的切线垂直，则的坐标为 ．
25．（2015·陕西·高考真题）函数在其极值点处的切线方程为 .
考点03 公切线问题
1．（2024·全国新Ⅰ卷·高考真题）若曲线在点处的切线也是曲线的切线，则 .
2．（2016·全国·高考真题）若直线是曲线的切线，也是曲线的切线，则 ．
3．（2015·全国·高考真题）已知曲线在点处的切线与曲线相切,则a= ．
考点04 利用导数判断函数单调性及其应用
1．（2024·全国新Ⅰ卷·高考真题）（多选）设函数，则（ ）
A．是的极小值点B．当时，
C．当时，D．当时，
2．（2023·全国新Ⅱ卷·高考真题）已知函数在区间上单调递增，则a的最小值为（ ）．
A．B．eC．D．
3．（2023·全国乙卷·高考真题）设，若函数在上单调递增，则a的取值范围是 .
4．（2019·北京·高考真题）设函数f（x）=ex+ae−x（a为常数）．若f（x）为奇函数，则a= ；若f（x）是R上的增函数，则a的取值范围是 ．
5．（2017·山东·高考真题）若函数(e=2.71828,是自然对数的底数)在的定义域上单调递增,则称函数具有M性质,下列函数中具有M性质的是
A．B．C．D．
6．（2016·全国·高考真题）若函数在上单调递增，则的取值范围是
A．B．C．D．
7．（2015·陕西·高考真题）设，则
A．既是奇函数又是减函数B．既是奇函数又是增函数
C．是有零点的减函数D．是没有零点的奇函数
8．（2015·福建·高考真题）若定义在上的函数满足，其导函数满足，则下列结论中一定错误的是（ ）
A．B．
C．D．
9．（2015·全国·高考真题）设函数是奇函数（）的导函数，，当时，，则使得成立的的取值范围是
A．B．
C．D．
考点05 求极值与最值及其应用
1．（2024·上海·高考真题）已知函数的定义域为R，定义集合，在使得的所有中，下列成立的是（ ）
A．存在是偶函数B．存在在处取最大值
C．存在是严格增函数D．存在在处取到极小值
2．（2023·全国新Ⅱ卷·高考真题）若函数既有极大值也有极小值，则（ ）．
A．B．C．D．
3．（2022·全国乙卷·高考真题）函数在区间的最小值、最大值分别为（ ）
A．B．C．D．
4．（2022·全国甲卷·高考真题）当时，函数取得最大值，则（ ）
A．B．C．D．1
5．（2021·全国新Ⅰ卷·高考真题）函数的最小值为 .
6．（2018·全国·高考真题）已知函数，则的最小值是 ．
7．（2018·江苏·高考真题）若函数在内有且只有一个零点，则在上的最大值与最小值的和为 ．
考点06 利用导数研究函数的极值点及其应用
1．（2022·全国新Ⅰ卷·高考真题）（多选）已知函数，则（ ）
A．有两个极值点B．有三个零点
C．点是曲线的对称中心D．直线是曲线的切线
2．（2022·全国乙卷·高考真题）已知和分别是函数（且）的极小值点和极大值点．若，则a的取值范围是 ．
3．（2021·全国乙卷·高考真题）设，若为函数的极大值点，则（ ）
A．B．C．D．
4．（2017·全国·高考真题）若是函数的极值点，则的极小值为．
A．B．C．D．
5．（2016·四川·高考真题）已知a为函数f（x）=x3–12x的极小值点，则a=
A．–4B．–2C．4D．2
考点07 导数与函数的基本性质结合问题
1．（2024·全国新Ⅰ卷·高考真题）（多选）设函数，则（ ）
A．是的极小值点B．当时，
C．当时，D．当时，
2．（2023·全国新Ⅰ卷·高考真题）（多选）已知函数的定义域为，，则（ ）．
A．B．
C．是偶函数D．为的极小值点
3．（2022·全国新Ⅰ卷·高考真题）（多选）已知函数及其导函数的定义域均为，记，若，均为偶函数，则（ ）
A．B．C．D．
4．（2021·全国新Ⅱ卷·高考真题）写出一个同时具有下列性质①②③的函数 ．
①；②当时，；③是奇函数．
5．（2017·山东·高考真题）若函数是自然对数的底数在的定义域上单调递增，则称函数具有M性质，下列函数中所有具有M性质的函数的序号为
① ② ③ ④
6．（2015·四川·高考真题）已知函数f（x）＝2x，g（x）＝x2＋ax（其中a∈R）.对于不相等的实数x1，x2，设m＝，n＝，现有如下命题：
①对于任意不相等的实数x1，x2，都有m＞0；
②对于任意的a及任意不相等的实数x1，x2，都有n＞0；
③对于任意的a，存在不相等的实数x1，x2，使得m＝n；
④对于任意的a，存在不相等的实数x1，x2，使得m＝－n.
其中真命题有 （写出所有真命题的序号）.
考点08 利用导数研究函数的零点及其应用
1．（2024·全国新Ⅱ卷·高考真题）（多选）设函数，则（ ）
A．当时，有三个零点
B．当时，是的极大值点
C．存在a，b，使得为曲线的对称轴
D．存在a，使得点为曲线的对称中心
2．（2023·全国乙卷·高考真题）函数存在3个零点，则的取值范围是（ ）
A．B．C．D．
3．（2021·北京·高考真题）已知函数，给出下列四个结论：
①若，恰 有2个零点；
②存在负数，使得恰有1个零点；
③存在负数，使得恰有3个零点；
④存在正数，使得恰有3个零点．
其中所有正确结论的序号是 ．
4．（2018·江苏·高考真题）若函数在内有且只有一个零点，则在上的最大值与最小值的和为 ．
5．（2017·全国·高考真题）已知函数有唯一零点，则
A．B．C．D．1
6．（2015·陕西·高考真题）对二次函数（为非零整数），四位同学分别给出下列结论，其中有且仅有一个结
论是错误的，则错误的结论是
A．是的零点B．1是的极值点
C．3是的极值D．点在曲线上
考点09 利用导数研究方程的根及其应用
1．（2024·全国甲卷·高考真题）曲线与在上有两个不同的交点，则的取值范围为 ．
2．（2021·北京·高考真题）已知函数，给出下列四个结论：
①若，恰 有2个零点；
②存在负数，使得恰有1个零点；
③存在负数，使得恰有3个零点；
④存在正数，使得恰有3个零点．
其中所有正确结论的序号是 ．
3．（2015·安徽·高考真题）函数的图象如图所示，则下列结论成立的是（ ）

A．，，，B．，，，
C．，，，D．，，，
4．（2015·全国·高考真题）设函数，其中 ，若存在唯一的整数，使得，则的取值范围是（ ）
A．B．C．D．
5．（2015·安徽·高考真题）设，其中均为实数，下列条件中，使得该三次方程仅有一个实根的是 .（写出所有正确条件的编号）
①；②；③；④；⑤.
考点10 构建函数利用导数判断函数单调性比较函数值大小关系
1．（2022·全国甲卷·高考真题）已知，则（ ）
A．B．C．D．
2．（2022·全国新Ⅰ卷·高考真题）设，则（ ）
A．B．C．D．
3．（2021·全国乙卷·高考真题）设，，．则（ ）
A．B．C．D．
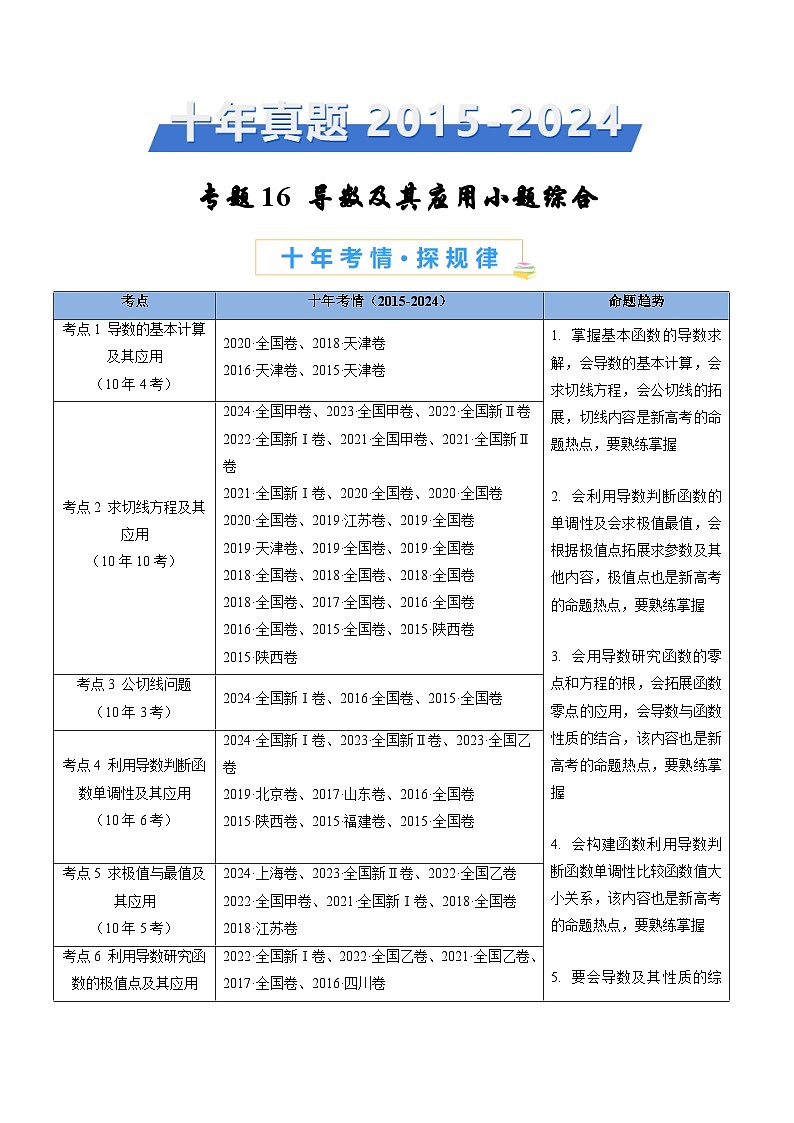
考点
十年考情（2015-2024）
命题趋势
考点1 导数的基本计算及其应用
（10年4考）
2020·全国卷、2018·天津卷
2016·天津卷、2015·天津卷
掌握基本函数的导数求解，会导数的基本计算，会求切线方程，会公切线的拓展，切线内容是新高考的命题热点，要熟练掌握
会利用导数判断函数的单调性及会求极值最值，会根据极值点拓展求参数及其他内容，极值点也是新高考的命题热点，要熟练掌握
会用导数研究函数的零点和方程的根，会拓展函数零点的应用，会导数与函数性质的结合，该内容也是新高考的命题热点，要熟练掌握
会构建函数利用导数判断函数单调性比较函数值大小关系，该内容也是新高考的命题热点，要熟练掌握
要会导数及其性质的综合应用，加强复习
考点2 求切线方程及其应用
（10年10考）
2024·全国甲卷、2023·全国甲卷、2022·全国新Ⅱ卷
2022·全国新Ⅰ卷、2021·全国甲卷、2021·全国新Ⅱ卷
2021·全国新Ⅰ卷、2020·全国卷、2020·全国卷
2020·全国卷、2019·江苏卷、2019·全国卷
2019·天津卷、2019·全国卷、2019·全国卷
2018·全国卷、2018·全国卷、2018·全国卷
2018·全国卷、2017·全国卷、2016·全国卷
2016·全国卷、2015·全国卷、2015·陕西卷
2015·陕西卷
考点3 公切线问题
（10年3考）
2024·全国新Ⅰ卷、2016·全国卷、2015·全国卷
考点4 利用导数判断函数单调性及其应用
（10年6考）
2024·全国新Ⅰ卷、2023·全国新Ⅱ卷、2023·全国乙卷
2019·北京卷、2017·山东卷、2016·全国卷
2015·陕西卷、2015·福建卷、2015·全国卷
考点5 求极值与最值及其应用
（10年5考）
2024·上海卷、2023·全国新Ⅱ卷、2022·全国乙卷
2022·全国甲卷、2021·全国新Ⅰ卷、2018·全国卷
2018·江苏卷
考点6 利用导数研究函数的极值点及其应用
（10年5考）
2022·全国新Ⅰ卷、2022·全国乙卷、2021·全国乙卷、2017·全国卷、2016·四川卷
考点7 导数与函数的基本性质结合问题
（10年6考）
2024·全国新Ⅰ卷、2023·全国新Ⅰ卷、2022·全国新Ⅰ卷
2021·全国新Ⅱ卷、2017·山东卷、2015·四川卷
考点8 利用导数研究函数的零点及其应用
（10年6考）
2024·全国新Ⅱ卷、2023·全国乙卷、2021·北京卷、2018·江苏卷、2017·全国卷、2015·陕西卷
考点9 利用导数研究方程的根及其应用
（10年3考）
2024·全国甲卷、2021·北京卷、2015·安徽卷
2015·全国卷、2015·安徽卷
考点10 构建函数利用导数判断函数单调性比较函数值大小关系
（10年3考）
2022·全国甲卷、2022·全国新Ⅰ卷、2021·全国乙卷