新高考数学一轮复习 讲与练第15讲 解三角形及其应用（2份打包，原卷版+解析版）

这是一份新高考数学一轮复习 讲与练第15讲 解三角形及其应用（2份打包，原卷版+解析版），文件包含新高考数学一轮复习讲与练第15讲解三角形及其应用原卷版doc、新高考数学一轮复习讲与练第15讲解三角形及其应用解析版doc等2份试卷配套教学资源，其中试卷共26页， 欢迎下载使用。

一、知识梳理
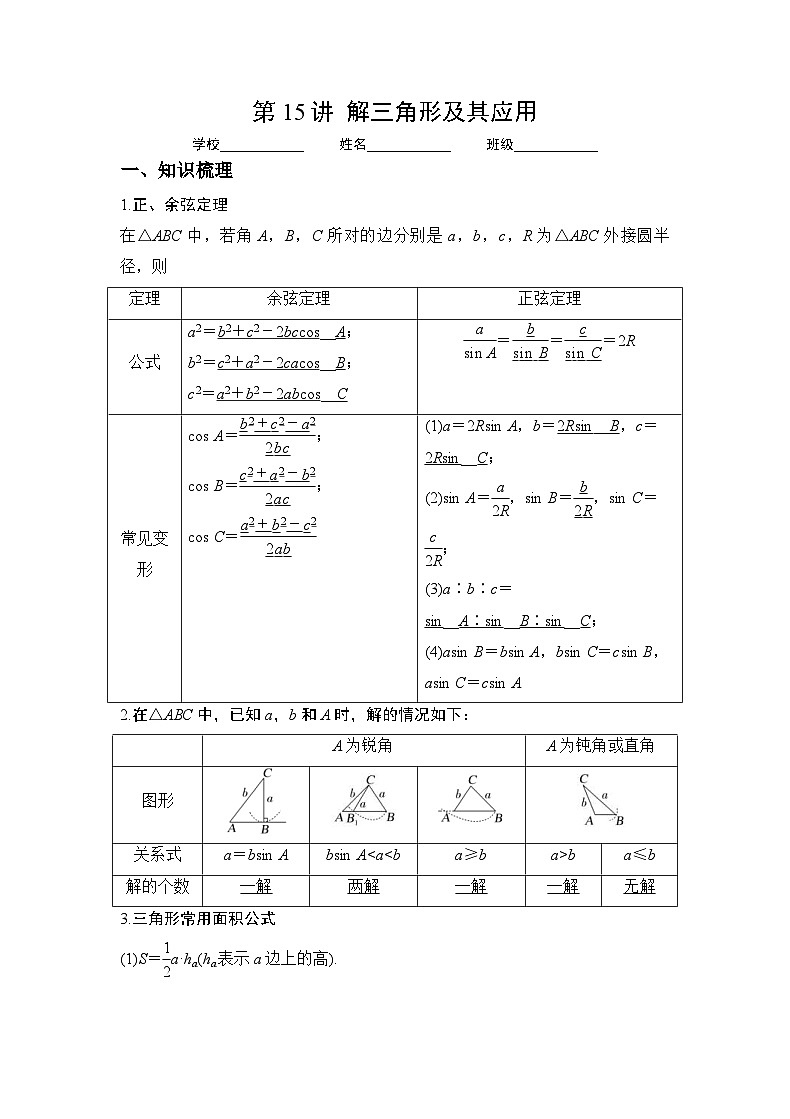
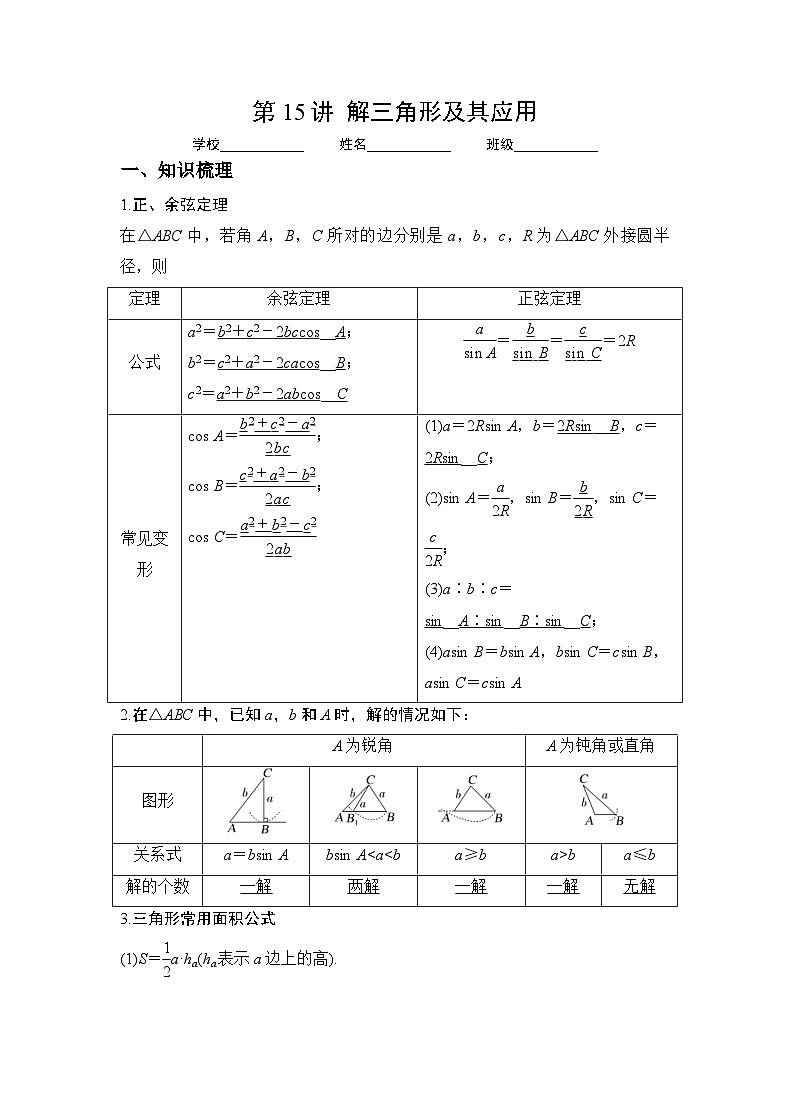
1.正、余弦定理
在△ABC中，若角A，B，C所对的边分别是a，b，c，R为△ABC外接圆半径，则
2.在△ABC中，已知a，b和A时，解的情况如下：
3.三角形常用面积公式
(1)S＝eq \f(1,2)a·ha(ha表示a边上的高).
(2)S＝eq \f(1,2)absin C＝eq \f(1,2)acsin B＝eq \f(1,2)bcsin A＝eq \f(abc,4R).
(3)S＝eq \f(1,2)r(a＋b＋c)(r为内切圆半径).
4.仰角和俯角
在同一铅垂平面内的水平视线和目标视线的夹角，目标视线在水平视线上方叫仰角，目标视线在水平视线下方叫俯角(如图1).
5.方位角
从正北方向起按顺时针转到目标方向线之间的水平夹角叫做方位角.如B点的方位角为α(如图2).
6.方向角
正北或正南方向线与目标方向线所成的锐角，如南偏东30°，北偏西45°等.
7.坡度：坡面与水平面所成的二面角的正切值.
考点和典型例题
1、利用正、余弦定理解三角形
【典例1-1】（2022·黑龙江·哈九中模拟预测（文））记 SKIPIF 1 < 0 的内角A，B，C的对边分别为a，b，c， SKIPIF 1 < 0 ， SKIPIF 1 < 0 , SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 的值为（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
【答案】C
【详解】
根据正弦定理得 SKIPIF 1 < 0 ，得 SKIPIF 1 < 0 SKIPIF 1 < 0 ，
所以 SKIPIF 1 < 0 SKIPIF 1 < 0 .
故选：C.
【典例1-2】（2022·江西·模拟预测（理））在△ABC中，内角A，B，C所对的边分别为a，b，c，且 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 的值为（ ）
A．4B．5C．6D．7
【答案】C
【详解】
由已知及正弦定理得 SKIPIF 1 < 0 ，所以 SKIPIF 1 < 0 ，所以 SKIPIF 1 < 0 ＝ SKIPIF 1 < 0 .
故选：C.
【典例1-3】（2022·黑龙江·哈九中模拟预测（理））记 SKIPIF 1 < 0 的内角A，B，C的对边分别为a，b，c， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ．则 SKIPIF 1 < 0 的值为（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0
C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
【答案】C
【详解】
在 SKIPIF 1 < 0 中，因为 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，
由正弦定理 SKIPIF 1 < 0 得： SKIPIF 1 < 0 ，解得： SKIPIF 1 < 0 .
因为 SKIPIF 1 < 0 ，所以 SKIPIF 1 < 0 .
所以 SKIPIF 1 < 0 .
故选：C
【典例1-4】（2022·河南·宝丰县第一高级中学模拟预测（文））在△ SKIPIF 1 < 0 中，角A，B，C的对边分别为a，b，c，且 SKIPIF 1 < 0 ，则角C的大小为（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
【答案】B
【详解】
因为 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 ，
整理得 SKIPIF 1 < 0 ，
所以 SKIPIF 1 < 0 即 SKIPIF 1 < 0 ，
则 SKIPIF 1 < 0 ，
∵ SKIPIF 1 < 0 ，所以 SKIPIF 1 < 0 .
故选：B.
【典例1-5】（2022·天津·耀华中学一模）在 SKIPIF 1 < 0 中，内角 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 所对的边分别为 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 .
(1)求 SKIPIF 1 < 0 的值；
(2)求 SKIPIF 1 < 0 ；
(3)求 SKIPIF 1 < 0 的值.
【答案】(1) SKIPIF 1 < 0 (2) SKIPIF 1 < 0 (3) SKIPIF 1 < 0
【解析】(1)
由余弦定理 SKIPIF 1 < 0 可得： SKIPIF 1 < 0 ，解得 SKIPIF 1 < 0 或 SKIPIF 1 < 0 （舍去），故 SKIPIF 1 < 0
(2)由正弦定理 SKIPIF 1 < 0 ,故 SKIPIF 1 < 0
(3)由（2）知： SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 ，故 SKIPIF 1 < 0 , SKIPIF 1 < 0
所以 SKIPIF 1 < 0
【典例1-6】（2022·陕西·西北工业大学附属中学模拟预测（理））如图，在平面四边形ABCD中，E为AD边上一点， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 .
(1)若 SKIPIF 1 < 0 ，求 SKIPIF 1 < 0 的值；
(2)若 SKIPIF 1 < 0 ，求BE的长.
【答案】(1) SKIPIF 1 < 0 (2) SKIPIF 1 < 0
【解析】(1)
过B作 SKIPIF 1 < 0 于F.
∵ SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 ，在直角 SKIPIF 1 < 0 中， SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 .
(2)连接BD.在 SKIPIF 1 < 0 中， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，由余弦定理，得
SKIPIF 1 < 0
在 SKIPIF 1 < 0 中， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，由余弦定理，得 SKIPIF 1 < 0 .
在 SKIPIF 1 < 0 中， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，由余弦定理，得 SKIPIF 1 < 0 .
∵ SKIPIF 1 < 0 ，得 SKIPIF 1 < 0
∴ SKIPIF 1 < 0 ，得 SKIPIF 1 < 0 ， SKIPIF 1 < 0 （负值舍去）.
∴ SKIPIF 1 < 0 .
【典例1-7】（2022·全国·高三专题练习（理））如图，在平面四边形ABCD中，对角线 SKIPIF 1 < 0 平分 SKIPIF 1 < 0 的内角A、B、C的对边分别为a、b、c.已知 SKIPIF 1 < 0 .
(1)求B；
(2)若 SKIPIF 1 < 0 ，且________，求线段 SKIPIF 1 < 0 的长.从下面①②中任选一个，补充在上面的空格中进行求解.①△ABC的面积 SKIPIF 1 < 0 ；② SKIPIF 1 < 0 .
【答案】(1) SKIPIF 1 < 0 ；(2)选① SKIPIF 1 < 0 ；选② SKIPIF 1 < 0 .
【解析】(1)
因为 SKIPIF 1 < 0 ，
所以 SKIPIF 1 < 0 ，
所以 SKIPIF 1 < 0 ，
所以 SKIPIF 1 < 0 ，
因为 SKIPIF 1 < 0 ，所以 SKIPIF 1 < 0 ，
所以 SKIPIF 1 < 0 ，
所以 SKIPIF 1 < 0 .
(2)选①，因为 SKIPIF 1 < 0 的面积 SKIPIF 1 < 0 ，
所以 SKIPIF 1 < 0 ，
即 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，由余弦定理得
所以 SKIPIF 1 < 0 ，
所以 SKIPIF 1 < 0 ，
因为 SKIPIF 1 < 0 平分 SKIPIF 1 < 0 ，
所以 SKIPIF 1 < 0 ，
所以 SKIPIF 1 < 0 ，
选②，因为 SKIPIF 1 < 0 ，在 SKIPIF 1 < 0 中，由余弦定理：
SKIPIF 1 < 0 ，
即 SKIPIF 1 < 0 ，
所以 SKIPIF 1 < 0 ，
因为 SKIPIF 1 < 0 ，
所以 SKIPIF 1 < 0 ，
因为 SKIPIF 1 < 0 平分 SKIPIF 1 < 0 ，所以 SKIPIF 1 < 0 ，
因为 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，由正弦定理得，
SKIPIF 1 < 0 ，所以 SKIPIF 1 < 0 ，
又 SKIPIF 1 < 0 ，所以 SKIPIF 1 < 0 ，
所以 SKIPIF 1 < 0 是直角三角形，且 SKIPIF 1 < 0 ，
所以 SKIPIF 1 < 0 .
2、判断三角形的形状
【典例2-1】（2022·江苏南通·模拟预测）小强计划制作一个三角形，使得它的三条边中线的长度分别为1， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，则（ ）
A．能制作一个锐角三角形B．能制作一个直角三角形
C．能制作一个钝角三角形D．不能制作这样的三角形
【答案】C
【详解】
设三角形的三条边为a，b，c，设 SKIPIF 1 < 0 中点为D，
SKIPIF 1 < 0 ，则 SKIPIF 1 < 0
SKIPIF 1 < 0 ，∴ SKIPIF 1 < 0
同理， SKIPIF 1 < 0
∴ SKIPIF 1 < 0 ，∴ SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，∴可以构成三角形
SKIPIF 1 < 0 ，∴ SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 为钝角三角形，
故选：C
【典例2-2】（2022·吉林·长春市第二实验中学高一期中）在 SKIPIF 1 < 0 中，角 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 所对的边分别为 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，下列结论正确的是（ ）
A．若 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 为锐角三角形
B．若 SKIPIF 1 < 0 为钝角三角形，则 SKIPIF 1 < 0
C．若 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 为等腰直角三角形
D．若 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，则符合条件的 SKIPIF 1 < 0 只有一个
【答案】D
【详解】
SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 ，只能说明A为锐角，
不能说明B和C的大小，故不能得到 SKIPIF 1 < 0 是锐角三角形，A错误；
若 SKIPIF 1 < 0 为钝角三角形，但不确定哪个角是钝角，若角A为锐角，则 SKIPIF 1 < 0 ，
若角A为钝角，则 SKIPIF 1 < 0 ，B错误；
SKIPIF 1 < 0 ，由正弦定理得： SKIPIF 1 < 0 ，即 SKIPIF 1 < 0 ，
所以 SKIPIF 1 < 0 或 SKIPIF 1 < 0 ，故 SKIPIF 1 < 0 或 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 为等腰三角形或直角三角形，故C错误；
由余弦定理得： SKIPIF 1 < 0 ，
因为 SKIPIF 1 < 0 ，所以 SKIPIF 1 < 0 ，故符合条件的 SKIPIF 1 < 0 只有1个，D正确.
故选：D
【典例2-3】（2022·辽宁·铁岭市清河高级中学高一期中）在 SKIPIF 1 < 0 中，已知 SKIPIF 1 < 0 ，那么 SKIPIF 1 < 0 一定是（ ）
A．等腰直角三角形B．等腰三角形C．等腰直角三角形D．等边三角形
【答案】B
【详解】
因为 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，
所以 SKIPIF 1 < 0 ，
所以由正余弦定理得 SKIPIF 1 < 0 ，化简得 SKIPIF 1 < 0 ，
所以 SKIPIF 1 < 0 ，
所以 SKIPIF 1 < 0 为等腰三角形.
故选：B.
【典例2-4】（2022·河南·安阳一中高一阶段练习）若在 SKIPIF 1 < 0 ，则三角形的形状一定是（ ）
A．直角三角形B．等腰三角形C．等腰直角三角形D．等边三角形
【答案】B
【详解】
由 SKIPIF 1 < 0 以及余弦定理得 SKIPIF 1 < 0 ，
化简得 SKIPIF 1 < 0 ，所以三角形的形状一定是等腰三角形.
故选：B
【典例2-5】（2022·全国·高一单元测试）在 SKIPIF 1 < 0 中，角 SKIPIF 1 < 0 、 SKIPIF 1 < 0 、 SKIPIF 1 < 0 的对边分别为 SKIPIF 1 < 0 、 SKIPIF 1 < 0 、 SKIPIF 1 < 0 ，若 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 是（ ）
A．钝角三角形B．等边三角形
C．直角三角形D．等腰直角三角形
【答案】B
【详解】
在 SKIPIF 1 < 0 中，由正弦定理得 SKIPIF 1 < 0 ，而 SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 ，即 SKIPIF 1 < 0 ，
又∵ SKIPIF 1 < 0 、 SKIPIF 1 < 0 为 SKIPIF 1 < 0 的内角，∴ SKIPIF 1 < 0 ，
又∵ SKIPIF 1 < 0 ，∴ SKIPIF 1 < 0 ，
∴由余弦定理得： SKIPIF 1 < 0 ，∴ SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 为等边三角形.
故选：B.
3、和三角形面积有关的问题
【典例3-1】（2022·江西·二模（理））在 SKIPIF 1 < 0 中，角A，B，C所对应的边分别为a，b，c，若 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 面积的最大值为( )
A．1B．3C．2D．4
【答案】C
【详解】
SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ，
即 SKIPIF 1 < 0 ，
即 SKIPIF 1 < 0 ，
则 SKIPIF 1 < 0 ，
整理得 SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 ，
当且仅当?2=3?2⇔?=83,?=83时取等号，
SKIPIF 1 < 0 ，
则 SKIPIF 1 < 0 ．
故选：C．
典例3-2】（2022·江西·模拟预测（文））在 SKIPIF 1 < 0 中， SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 的面积为（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
【答案】B
【详解】
由余弦定理得 SKIPIF 1 < 0 ，
即 SKIPIF 1 < 0 ，解得 SKIPIF 1 < 0 ，
因为 SKIPIF 1 < 0 ，所以 SKIPIF 1 < 0 ，
所以 SKIPIF 1 < 0 ，
故选：B．
典例3-3】（2022·江西宜春·模拟预测（文）） SKIPIF 1 < 0 的内角 SKIPIF 1 < 0 的对边分别为 SKIPIF 1 < 0 ，若 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 的面积为（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
【答案】C
【详解】
解：由余弦定理 SKIPIF 1 < 0 ，即 SKIPIF 1 < 0 ，又 SKIPIF 1 < 0 ，
所以 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，所以 SKIPIF 1 < 0 .
故选：C
典例3-4】（2022·内蒙古赤峰·三模（文）） SKIPIF 1 < 0 的三个内角 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 的对边分别为 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 且 SKIPIF 1 < 0
(1)求 SKIPIF 1 < 0 ；
(2)若 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，求 SKIPIF 1 < 0 的面积．
【答案】(1) SKIPIF 1 < 0 ；(2) SKIPIF 1 < 0 .
【解析】(1)
由 SKIPIF 1 < 0 及正弦定理，得
SKIPIF 1 < 0 ，即 SKIPIF 1 < 0 ，于是有 SKIPIF 1 < 0 ，
由余弦定理，得 SKIPIF 1 < 0 ，
SKIPIF 1 < 0
(2)由（1）知， SKIPIF 1 < 0 ，及 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，
由余弦定理，得 SKIPIF 1 < 0 ，即 SKIPIF 1 < 0 ，
化简整理，得 SKIPIF 1 < 0 ，解得 SKIPIF 1 < 0 或 SKIPIF 1 < 0 （舍）.
所以 SKIPIF 1 < 0 .
所以 SKIPIF 1 < 0 的面积为 SKIPIF 1 < 0 .
典例3-5】（2022·湖南·模拟预测）在 SKIPIF 1 < 0 中，角A，B，C所对的边分别为a，b，c，已知 SKIPIF 1 < 0 ．
(1)求证： SKIPIF 1 < 0 ；
(2)若 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，且 SKIPIF 1 < 0 ，求 SKIPIF 1 < 0 的面积．
【解析】(1)
解：因为 SKIPIF 1 < 0 ，
由正弦定理可得： SKIPIF 1 < 0 ，
所以 SKIPIF 1 < 0 ；
(2)
由（1）得 SKIPIF 1 < 0 ，
由余弦定理得： SKIPIF 1 < 0 ，
所以 SKIPIF 1 < 0 ，即 SKIPIF 1 < 0 ，
将 SKIPIF 1 < 0 ， SKIPIF 1 < 0 代入，得 SKIPIF 1 < 0 ，
即 SKIPIF 1 < 0 ，
解得 SKIPIF 1 < 0 或 SKIPIF 1 < 0 ，
∵ SKIPIF 1 < 0 ，∴ SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 舍去，
∴ SKIPIF 1 < 0 ， SKIPIF 1 < 0 ．
从而 SKIPIF 1 < 0 ，
由 SKIPIF 1 < 0 可知 SKIPIF 1 < 0 ，
所以 SKIPIF 1 < 0 ．
所以 SKIPIF 1 < 0 的面积 SKIPIF 1 < 0 ．
4、解三角形的实际应用
【典例4-1】（2022·吉林吉林·模拟预测（文））位于灯塔A处正西方向相距 SKIPIF 1 < 0 n mile的B处有一艘甲船需要海上救援，位于灯塔A处北偏东45°相距 SKIPIF 1 < 0 n mile的C处的一艘乙船前往营救，则乙船的目标方向线（由观测点看目标的视线）的方向是南偏西（ ）
A．30°B．60°C．75°D．45°
【答案】B
【详解】
依题意，过点 SKIPIF 1 < 0 作 SKIPIF 1 < 0 的延长线交于点 SKIPIF 1 < 0 ，如图，
则 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，
在 SKIPIF 1 < 0 中， SKIPIF 1 < 0 ，
在 SKIPIF 1 < 0 中， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，
SKIPIF 1 < 0 又 SKIPIF 1 < 0
SKIPIF 1 < 0 ，
则乙船的目标方向线（由观测点看目标的视线）的方向是南偏西60°.
故选：B.
【典例4-2】（2022·江西·模拟预测（文））翠浪塔，位于赣州市章江西岸杨梅渡公园山顶上，与赣州古城的风水塔——玉虹塔相呼应．塔名源于北宋大文豪苏东坡吟咏赣州的诗句“山为翠浪涌，水作玉虹流”，该塔规划设计为仿宋塔建筑风格，塔体八面．一研学小组在李老师的带领下到该塔参观，这时李老师（身高约1.7米）站在一个地方（脚底与塔底在同一平面）面朝塔顶，仰角约为45 SKIPIF 1 < 0 ；当他水平后退50米后再次观测塔顶，仰角约为30 SKIPIF 1 < 0 ，据此李老师问：同学们，翠浪塔高度大约为（ ）米？（参考数据： SKIPIF 1 < 0 ）
A．68B．70C．72D．74
【答案】B
【详解】
如图所示，OP为塔体，AC,BD为李老师观察塔顶时的站位， Q为A,B在OP上的射影，
由已知得 SKIPIF 1 < 0 为直角三角形， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 (米)， SKIPIF 1 < 0 (米),设PQ=x，则 SKIPIF 1 < 0 , SKIPIF 1 < 0 .
∴ SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 ,
∴塔高 SKIPIF 1 < 0 (米),
故选：B
【典例4-3】（2022·全国·高三专题练习）设M，N为某海边相邻的两座山峰，到海平面的距离分别为100米，50米．现欲在M，N之间架设高压电网，须计算M，N之间的距离．勘测人员在海平面上选取一点P，利用测角仪从P点测得的M，N点的仰角分别为30°，45°，并从P点观测到M，N点的视角为45°，则M，N之间的距离为（ ）
A． SKIPIF 1 < 0 米B． SKIPIF 1 < 0 米C． SKIPIF 1 < 0 米D． SKIPIF 1 < 0 米
【答案】A
【详解】
如图，由题可知 SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，又 SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 （米）．
故选：A.
【典例4-4】（2022·陕西·西安中学一模（理））为了测量隧道口 SKIPIF 1 < 0 、 SKIPIF 1 < 0 间的距离，开车从 SKIPIF 1 < 0 点出发，沿正西方向行驶 SKIPIF 1 < 0 米到达 SKIPIF 1 < 0 点，然后从 SKIPIF 1 < 0 点出发，沿正北方向行驶一段路程后到达 SKIPIF 1 < 0 点，再从 SKIPIF 1 < 0 点出发，沿东南方向行驶400米到达隧道口 SKIPIF 1 < 0 点处，测得 SKIPIF 1 < 0 间的距离为1000米.
(1)若隧道口 SKIPIF 1 < 0 在点 SKIPIF 1 < 0 的北偏东 SKIPIF 1 < 0 度的方向上，求 SKIPIF 1 < 0 的值；
(2)求隧道口 SKIPIF 1 < 0 间的距离.
【答案】(1) SKIPIF 1 < 0 (2)1000米.
【解析】(1)
在 SKIPIF 1 < 0 中，由正弦定理得 SKIPIF 1 < 0 ，
即 SKIPIF 1 < 0 ，
所以 SKIPIF 1 < 0 ，
由题可知， SKIPIF 1 < 0 ，
所以 SKIPIF 1 < 0 ，即 SKIPIF 1 < 0 .
(2)由（1）可知， SKIPIF 1 < 0 ，
在 SKIPIF 1 < 0 中，由余弦定理得 SKIPIF 1 < 0
SKIPIF 1 < 0 ，
所以 SKIPIF 1 < 0 ，
故两隧道口 SKIPIF 1 < 0 间的距离为1000米.
【典例4-5】（2022·广东湛江·二模）如图，一架飞机从 SKIPIF 1 < 0 地飞往 SKIPIF 1 < 0 地，两地相距 SKIPIF 1 < 0 .飞行员为了避开某一区域的雷雨云层，从机场起飞以后，就沿与原来的飞行方向成 SKIPIF 1 < 0 角的方向飞行，飞行到 SKIPIF 1 < 0 地，再沿与原来的飞行方向成 SKIPIF 1 < 0 角的方向继续飞行 SKIPIF 1 < 0 到达终点.
(1)求 SKIPIF 1 < 0 、 SKIPIF 1 < 0 两地之间的距离；
(2)求 SKIPIF 1 < 0 .
【答案】(1) SKIPIF 1 < 0 (2) SKIPIF 1 < 0
【解析】(1)
解：由余弦定理可得 SKIPIF 1 < 0 ，
所以， SKIPIF 1 < 0 .
(2)解：由余弦定理可得 SKIPIF 1 < 0 ，
所以， SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 为锐角，故 SKIPIF 1 < 0 ，
因此， SKIPIF 1 < 0 .
定理
余弦定理
正弦定理
公式
a2＝b2＋c2－2bccs__A；
b2＝c2＋a2－2cacs__B；
c2＝a2＋b2－2abcs__C
eq \f(a,sin A)＝eq \f(b,sin B)＝eq \f(c,sin C)＝2R
常见变形
cs A＝eq \f(b2＋c2－a2,2bc)；
cs B＝eq \f(c2＋a2－b2,2ac)；
cs C＝eq \f(a2＋b2－c2,2ab)
(1)a＝2Rsin A，b＝2Rsin__B，c＝2Rsin__C；
(2)sin A＝eq \f(a,2R)，sin B＝eq \f(b,2R)，sin C＝eq \f(c,2R)；
(3)a∶b∶c＝sin__A∶sin__B∶sin__C；
(4)asin B＝bsin A，bsin C＝csin B，asin C＝csin A
A为锐角
A为钝角或直角
图形
关系式
a＝bsin A
bsin Aa≥b
a>b
a≤b
解的个数
一解
两解
一解
一解
无解