四川省宜宾市2024届高三下学期高考适应性考试（三模）文科数学试卷（原卷版）

这是一份四川省宜宾市2024届高三下学期高考适应性考试（三模）文科数学试卷（原卷版），共5页。试卷主要包含了考试结束后，将答题卡交回等内容，欢迎下载使用。

（考试时间：120分钟 全卷满分：150分）
注意事项：
1．答卷前，考生务必用黑色签字笔将自己的姓名、准考证号、考场号、座位号填写在答题卡上，并认真核准条形码上的准考证号、姓名、考场号、座位号及科目，在规定的位置贴好条形码．
2．回答选择题时，选出每小题答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑．如需改动，用橡皮擦擦干净后，再选涂其它答案标号．回答非选择题时，将答案写在答题卡上，写在本试卷上无效．
3．考试结束后，将答题卡交回．
一、选择题：本题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项符合要求．
1. 已知集合，，则（ ）
A. B. C. D.
2. 已知复数z满足且是z的共轭复数，则（ ）
A. B. 1C. D.
3. 已知一组数据，，，，的平均数是，方差是，则对于以下数据：，，，，下列选项正确的是（ ）
A. 平均数是，方差是6B. 平均数是，方差是
C. 平均数是5，方差是D. 平均数是5，方差是12
4. 若曲线的一条切线方程是，则（ ）
A. B. 1C. D. e
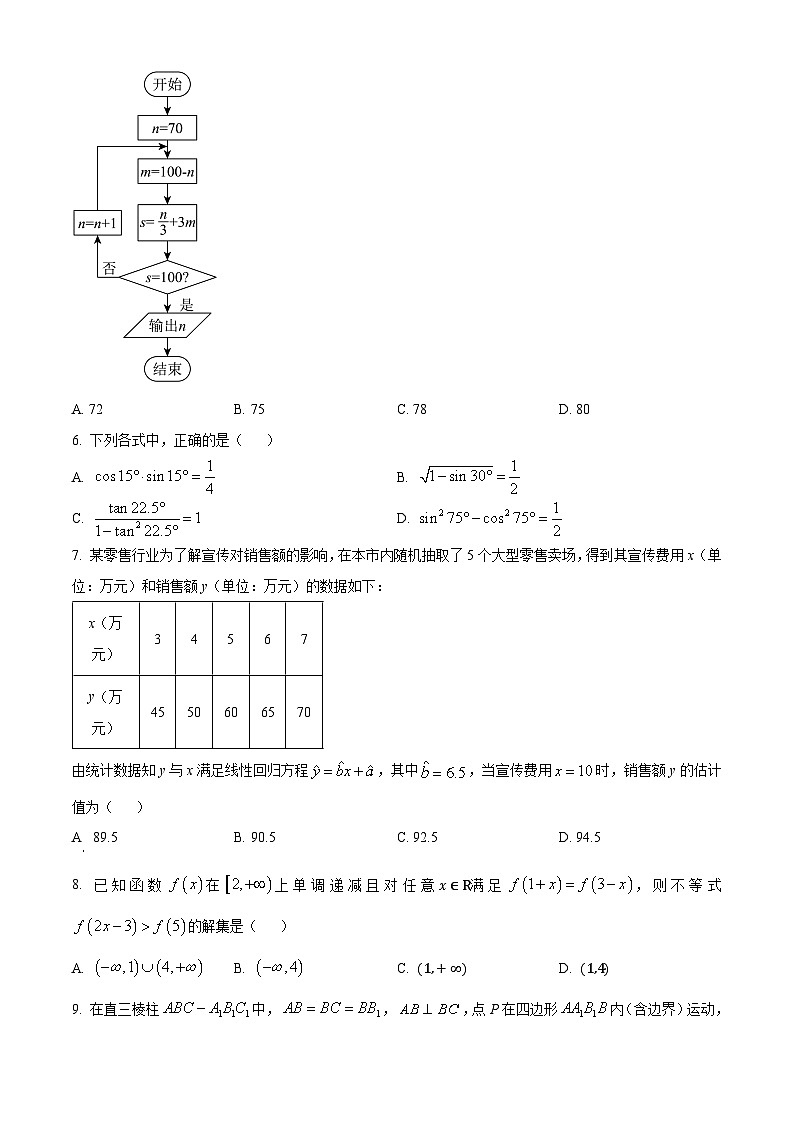
5. 明朝数学家程大位著的《算法统宗》里有一道著名的题目：“一百馒头一百僧，大僧三个更无争，小僧三人分一个，大、小和尚各几丁？”如图所示的程序框图反映了此题的一个算法，执行图中的程序框图，则输出n＝（ ）
A. 72B. 75C. 78D. 80
6. 下列各式中，正确的是（ ）
A. B.
C. D.
7. 某零售行业为了解宣传对销售额的影响，在本市内随机抽取了5个大型零售卖场，得到其宣传费用x（单位：万元）和销售额y（单位：万元）的数据如下：
由统计数据知y与x满足线性回归方程，其中，当宣传费用时，销售额y的估计值为（ ）
A 89.5B. 90.5C. 92.5D. 94.5
8. 已知函数在上单调递减且对任意x∈R满足，则不等式的解集是（ ）
A. B. C. 1,+∞D. 1,4
9. 在直三棱柱中，，，点P在四边形内（含边界）运动，当时，点P的轨迹长度为，则该三棱柱的表面积为（ ）
A. 4B. C. D.
10. 已知抛物线C：，过动点P作两条相互垂直的直线，分别与抛物线C相切，则点P的轨迹是（ ）
A. 一条抛物线B. 一个圆C. 一条直线D. 一段线段
11. 定义在上的单调函数，对任意的有恒成立，若方程有两个不同的实数根，则实数的取值范围为（ ）
A. B. C. D.
12. 已知E，F分别是棱长为2的正四面体的对棱的中点.过的平面与正四面体相截，得到一个截面多边形，则下列说法正确的是（ ）
A. 截面多边形不可能是平行四边形B. 截面多边形的周长是定值
C. 截面多边形的周长的最小值是D. 截面多边形的面积的取值范围是
二、填空题：本大题共4个小题，每小题5分，共20分．
13. 若，则的最小值为______．
14. 已知数列是公差不为0的等差数列，，且满足成等比数列，则数列前6项的和为__________.
15. 已知为双曲线的左､右焦点，为双曲线右支上任意一点，点的坐标为.若有最大值，则双曲线的离心率的取值范围是__________.
16. 已知点O，A，B，C均在同一平面内，，，，当取最大值时，______．
三、解答题：共70分．解答应写出文字说明、证明过程或演算步骤．第17-21题为必考题，每个试题考生都必须作答．第22、23题为选考题，考生根据要求作答．
（一）必做题：共60分．
17. 某地为调查年龄在35―50岁段人群每周的运动情况，从年龄在35―50岁段人群中随机抽取了200人的信息，将调查结果整理如下：
（1）根据以上信息，能否有99%把握认为该地年龄在35―50岁段人群每周运动超过2小时与性别有关？
（2）在以上被抽取且每周运动不超过2小时的人中，按性别进行分层抽样，共抽6人．再从这6人中随机抽取2人进行访谈，求这2人中至少有1人是女性的概率．
参考公式：，．
18 已知数列满足.
（1）证明：数列是等比数列，并求出数列的通项公式；
（2）设，数列的前项和为，若对于任意恒成立，求实数的取值范围.
19. 如图，在四棱锥中，底面是正方形，，，，点E为线段的中点，点F在线段AB上，且．
（1）求证：；
（2）求三棱锥的体积．
20. 已知函数．
（1）当时，求函数过原点的切线方程；
（2）若有三个零点，求a的取值范围．
21. 已知椭圆E：左右焦点分别为，，过焦点斜率为的直线与椭圆E交于A，B两点，过焦点斜率为的直线与椭圆E交于C，D两点，且．
（1）求直线与的交点N的轨迹M的方程；
（2）若直线OA，OB，OC，OD斜率分别为，，，，问在（1）的轨迹M上是否存在点P，满足，若存在，求出点P坐标；若不存在，说明理由．
（二）选做题：共10分．请考生在第22、23题中选一题作答．如果多做，则按所做的第一题计分．
［选修4-4：坐标系与参数方程］
22. 在平面直角坐标系中，过点的直线的参数方程为（为参数）.以原点为极点，轴的正半轴为极轴建立极坐标系，曲线的极坐标方程为.直线与曲线相交于两点.
（1）求直线的普通方程及曲线的直角坐标方程；
（2）若成等比数列，求实数的值.
［选修4-5：不等式选讲］
23. 已知函数．
（1）求的最小值；
（2）若恒成立，求实数的取值范围．x（万元）
3
4
5
6
7
y（万元）
45
50
60
65
70
女性
男性
每周运动超过2小时
60
80
每周运动不超过2小时
40
20
0.10
0.05
0.025
0.010
0.001
2.706
3.841
5.024
6635
10.828