专题31 规律型探究题（24题）（教师卷+学生卷）- 2024年中考数学真题分类汇编（全国通用）

这是一份专题31 规律型探究题（24题）（教师卷+学生卷）- 2024年中考数学真题分类汇编（全国通用），文件包含专题31规律型探究题24题教师卷-2024年中考数学真题分类汇编全国通用docx、专题31规律型探究题24题学生卷-2024年中考数学真题分类汇编全国通用docx等2份试卷配套教学资源，其中试卷共31页， 欢迎下载使用。

一、单选题
1．（2024·云南·中考真题）按一定规律排列的代数式：，，，，，，第个代数式是（ ）
A．B．C．D．
【答案】D
【分析】本题考查了数列的规律变化，根据数列找到变化规律即可求解，仔细观察和总结规律是解题的关键．
【详解】解：∵按一定规律排列的代数式：，，，，，，
∴第个代数式是，
故选：．
2．（2024·重庆·中考真题）烷烃是一类由碳、氢元素组成的有机化合物质，下图是这类物质前四种化合物的分子结构模型图，其中灰球代表碳原子，白球代表氢原子．第1种如图①有4个氢原子，第2种如图②有6个氢原子，第3种如图③有8个氢原子，……按照这一规律，第10种化合物的分子结构模型中氢原子的个数是（ ）
A．20B．22C．24D．26
【答案】B
【分析】本题考查数字的变化类，根据图形，可归纳出规律表达式的特点，再解答即可．
【详解】解：由图可得，
第1种如图①有4个氢原子，即
第2种如图②有6个氢原子，即
第3种如图③有8个氢原子，即
，
第10种化合物的分子结构模型中氢原子的个数是：；
故选：B．
3．（2024·重庆·中考真题）用菱形按如图所示的规律拼图案，其中第①个图案中有2个菱形，第②个图案中有5个菱形，第③个图案中有8个菱形，第④个图案中有11个菱形，…，按此规律，则第⑧个图案中，菱形的个数是（ ）
A．20B．21C．23D．26
【答案】C
【分析】本题考查了图形类的规律探索，解题的关键是找出规律．利用规律求解．通过观察图形找到相应的规律，进行求解即可．
【详解】解：第①个图案中有个菱形，
第②个图案中有个菱形，
第③个图案中有个菱形，
第④个图案中有个菱形，
∴第个图案中有个菱形，
∴第⑧个图案中菱形的个数为，
故选：C．
4．（2024·黑龙江牡丹江·中考真题）如图是由一些同样大小的三角形按照一定规律所组成的图形，第1个图有4个三角形．第2个图有7个三角形，第3个图有10个三角形……按照此规律排列下去，第674个图中三角形的个数是（ ）
A．2022B．2023C．2024D．2025
【答案】B
【分析】此题考查了图形的变化规律，解题的关键是根据图形的排列，归纳出图形的变化规律．根据前几个图形的变化发现规律，可用含n的代数式表示出第n个图形中三角形的个数，从而可求第674个图形中三角形的个数．
【详解】解：第1个图案有4个三角形，即，
第2个图案有7个三角形，即，
第3个图案有10个三角形，即，
…，
按此规律摆下去，第n个图案有个三角形，
则第674个图案中三角形的个数为：（个）．
故选：B．
5．（2024·湖北武汉·中考真题）如图，小好同学用计算机软件绘制函数的图象，发现它关于点中心对称．若点，，，……，，都在函数图象上，这个点的横坐标从开始依次增加，则的值是（ ）
A．B．C．0D．1
【答案】D
【分析】本题是坐标规律题，求函数值，中心对称的性质，根据题意得出，进而转化为求，根据题意可得，，即可求解．
【详解】解：∵这个点的横坐标从开始依次增加，
∴，
∴，
∴，而即，
∵，
当时，，即，
∵关于点中心对称的点为，
即当时，，
∴，
故选：D．
6．（2024·四川德阳·中考真题）将一组数，按以下方式进行排列：
则第八行左起第1个数是（ ）
A．B．C．D．
【答案】C
【分析】本题考查了数字类规律探索，正确归纳类推出一般规律是解题关键．求出第七行共有28个数，从而可得第八行左起第1个数是第29个数，据此求解即可得．
【详解】解：由图可知，第一行共有1个数，第二行共有2个数，第三行共有3个数，
归纳类推得：第七行共有个数，
则第八行左起第1个数是，
故选：C．
7．（2024·江苏扬州·中考真题）1202年数学家斐波那契在《计算之书》中记载了一列数：1，1，2，3，5，……，这一列数满足：从第三个数开始，每一个数都等于它的前两个数之和．则在这一列数的前2024个数中，奇数的个数为（ ）
A．676B．674C．1348D．1350
【答案】D
【分析】将这一列数继续写下去，发现这列数的变化规律即可解答．
本题主要考查的是数字规律类问题，发现这列数的变化规律是解题的关键．
【详解】这一列数为：1，1，2，3，5，8，13，21，34，…
可以发现每3个数为一组，每一组前2个数为奇数，第3个数为偶数．
由于，
即前2024个数共有674组，且余2个数，
∴奇数有个．
故选：D
8．（2024·河北·中考真题）平面直角坐标系中，我们把横、纵坐标都是整数，且横、纵坐标之和大于0的点称为“和点”．将某“和点”平移，每次平移的方向取决于该点横、纵坐标之和除以3所得的余数（当余数为0时，向右平移；当余数为1时，向上平移；当余数为2时，向左平移），每次平移1个单位长度．
若“和点”Q按上述规则连续平移16次后，到达点，则点Q的坐标为（ ）
A．或B．或C．或D．或
【答案】D
【分析】本题考查了坐标内点的平移运动，熟练掌握知识点，利用反向运动理解是解决本题的关键．
先找出规律若“和点”横、纵坐标之和除以3所得的余数为0时，先向右平移1个单位，之后按照向上、向左，向上、向左不断重复的规律平移，按照的反向运动理解去分类讨论：①先向右1个单位，不符合题意；②先向下1个单位，再向右平移，当平移到第15次时，共计向下平移了8次，向右平移了7次，此时坐标为，那么最后一次若向右平移则为，若向左平移则为．
【详解】解：由点可知横、纵坐标之和除以3所得的余数为1，继而向上平移1个单位得到，此时横、纵坐标之和除以3所得的余数为2，继而向左平移1个单位得到，此时横、纵坐标之和除以3所得的余数为1，又要向上平移1个单位，因此发现规律为若“和点”横、纵坐标之和除以3所得的余数为0时，先向右平移1个单位，之后按照向上、向左，向上、向左不断重复的规律平移，
若“和点”Q按上述规则连续平移16次后，到达点，则按照“和点”反向运动16次求点Q坐标理解，可以分为两种情况：
①先向右1个单位得到，此时横、纵坐标之和除以3所得的余数为0，应该是向右平移1个单位得到，故矛盾，不成立；
②先向下1个单位得到，此时横、纵坐标之和除以3所得的余数为1，则应该向上平移1个单位得到，故符合题意，那么点先向下平移，再向右平移，当平移到第15次时，共计向下平移了8次，向右平移了7次，此时坐标为，即，那么最后一次若向右平移则为，若向左平移则为，
故选：D．
9．（2024·重庆·中考真题）已知整式，其中为自然数，为正整数，且．下列说法：
①满足条件的整式中有5个单项式；
②不存在任何一个，使得满足条件的整式有且只有3个；
③满足条件的整式共有16个．
其中正确的个数是（ ）
A．0B．1C．2D．3
【答案】D
【分析】本题考查的是整式的规律探究，分类讨论思想的应用，由条件可得，再分类讨论得到答案即可．
【详解】解：∵为自然数，为正整数，且，
∴，
当时，则，
∴，，
满足条件的整式有，
当时，则，
∴，，，，
满足条件的整式有：，，，，
当时，则，
∴，，，，，，
满足条件的整式有：，，，，，；
当时，则，
∴，，，，
满足条件的整式有：，，，；
当时，，
满足条件的整式有：；
∴满足条件的单项式有：，，，，，故①符合题意；
不存在任何一个，使得满足条件的整式有且只有3个；故②符合题意；
满足条件的整式共有个．故③符合题意；
故选D
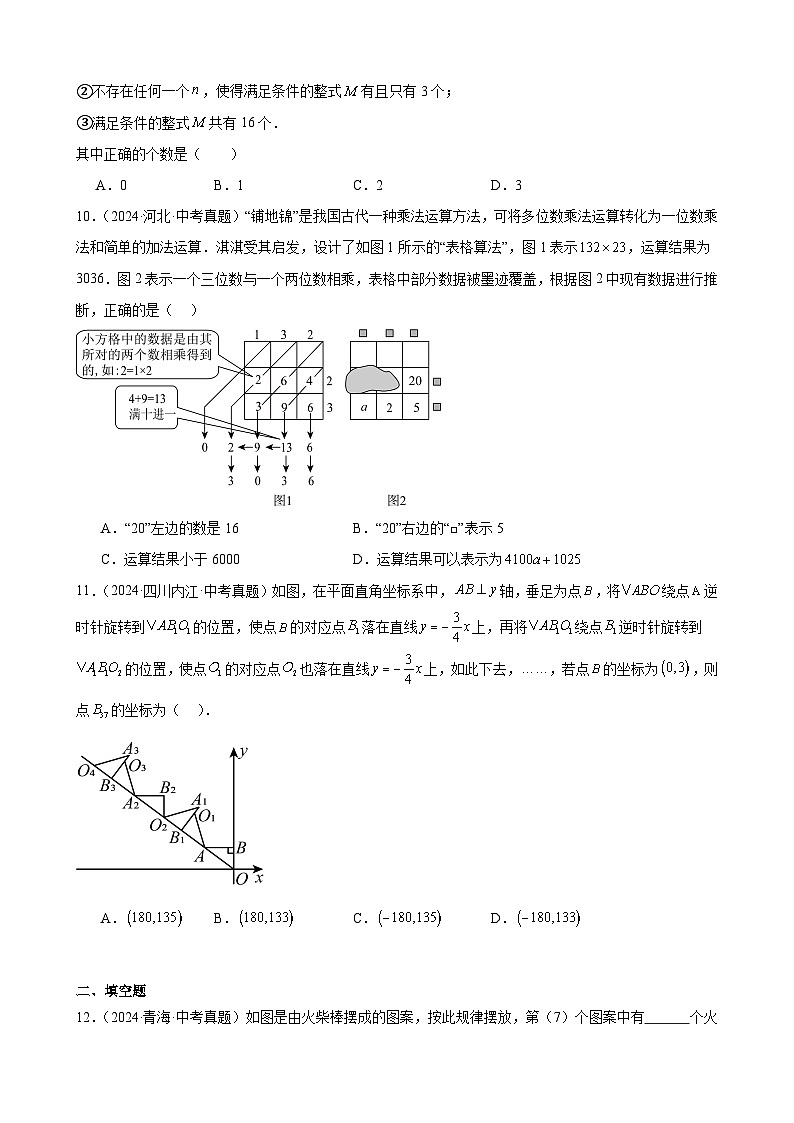
10．（2024·河北·中考真题）“铺地锦”是我国古代一种乘法运算方法，可将多位数乘法运算转化为一位数乘法和简单的加法运算．淇淇受其启发，设计了如图1所示的“表格算法”，图1表示，运算结果为3036．图2表示一个三位数与一个两位数相乘，表格中部分数据被墨迹覆盖，根据图2中现有数据进行推断，正确的是（ ）
A．“20”左边的数是16B．“20”右边的“□”表示5
C．运算结果小于6000D．运算结果可以表示为
【答案】D
【分析】本题考查了整式的加法运算，整式的乘法运算，理解题意，正确的逻辑推理时解决本题的关键．
设一个三位数与一个两位数分别为和，则，即，可确定时，则，由题意可判断A、B选项，根据题意可得运算结果可以表示为：，故可判断C、D选项．
【详解】解：设一个三位数与一个两位数分别为和
如图：
则由题意得：
，
∴，即，
∴当时，不是正整数，不符合题意，故舍；
当时，则，如图：
，
∴A、“20”左边的数是，故本选项不符合题意；
B、“20”右边的“□”表示4，故本选项不符合题意；
∴上面的数应为，如图：
∴运算结果可以表示为：，
∴D选项符合题意，
当时，计算的结果大于6000，故C选项不符合题意，
故选：D．
11．（2024·四川内江·中考真题）如图，在平面直角坐标系中，轴，垂足为点，将绕点逆时针旋转到的位置，使点的对应点落在直线上，再将绕点逆时针旋转到的位置，使点的对应点也落在直线上，如此下去，……，若点的坐标为，则点的坐标为（ ）．
A．B．C．D．
【答案】C
【分析】本题考查了平面直角坐标系、一次函数、旋转的性质、勾股定理等知识点．找出点的坐标规律以及旋转过程中线段长度的关系是解题的关键．
通过求出点的坐标，、、的长度，再根据旋转的特点逐步推导出后续点的位置和坐标，然后结合图形求解即可．
【详解】轴，点的坐标为，
，则点的纵坐标为3，代入，
得：，则点的坐标为．
，，
，
由旋转可知，，，，
，，
，
．
设点的坐标为，
则，
解得或（舍去），则，
点的坐标为．
故选C．
二、填空题
12．（2024·青海·中考真题）如图是由火柴棒摆成的图案，按此规律摆放，第（7）个图案中有 个火柴棒．

【答案】15
【分析】本题考查图形类规律探究．根据题意得到第（1）、（2）、（3）个图形中火柴棒的数量，由此可得第（n）个图形有根火柴棒，即可．
【详解】解：根据题意得：第（1）个图形有根火柴棒，
第（2）个图形有根火柴棒，
第（3）个图形有根火柴棒，
……
第（n）个图形有根火柴棒，
∴第（7）个图案中有根火柴棒，
故答案为：15
13．（2024·江西·中考真题）观察a，，，，…，根据这些式子的变化规律，可得第100个式子为 ．
【答案】
【分析】此题考查了单项式规律探究．分别找出系数和次数的规律，据此判断出第n个式子是多少即可．
【详解】解：∵a，，，，…，
∴第n个单项式的系数是1；
∵第1个、第2个、第3个、第4个单项式的次数分别是1、2、3、4，…，
∴第n个式子是．
∴第100个式子是．
故答案为：．
14．（2024·山东·中考真题）任取一个正整数，若是奇数，就将该数乘3再加上1；若是偶数，就将该数除以2．反复进行上述两种运算，经过有限次运算后，必进入循环圈1→4→2→1，这就是“冰雹猜想”．在平面直角坐标系中，将点中的，分别按照“冰雹猜想”同步进行运算得到新的点的横、纵坐标，其中，均为正整数．例如，点经过第1次运算得到点，经过第2次运算得到点，以此类推．则点经过2024次运算后得到点 ．
【答案】
【分析】本题考查了新定义，点的规律，根据新定义依次计算出各点的坐标，然后找出规律，最后应用规律求解即可．
【详解】解：点经过1次运算后得到点为，即为，
经过2次运算后得到点为，即为，
经过3次运算后得到点为，即为，
……，
发现规律：点经过3次运算后还是，
∵，
∴点经过2024次运算后得到点，
故答案为：．
15．（2024·黑龙江齐齐哈尔·中考真题）如图，数学活动小组在用几何画板绘制几何图形时，发现了如“花朵”形的美丽图案，他们将等腰三角形OBC置于平面直角坐标系中，点O的坐标为，点B的坐标为，点C在第一象限，．将沿x轴正方向作无滑动滚动，使它的三边依次与x轴重合，第一次滚动后，点O的对应点为，点C的对应点为，与的交点为，称点为第一个“花朵”的花心，点为第二个“花朵”的花心；……；按此规律，滚动2024次后停止滚动，则最后一个“花朵”的花心的坐标为 ．
【答案】
【分析】本题考查了解直角三角形，等腰直角的性质，点的坐标规律探索．连接，求得，，，分别得到，， ，，推导得到，滚动一次得到，滚动四次得到，滚动七次得到，由此得到滚动2024次后停止滚动，则，据此求解即可．
【详解】解：连接，
由题意得，，，
∴，
∴，，，
∴，
∴，
，
同理，
，
，
滚动一次得到，滚动四次得到，滚动七次得到，
∴滚动2024次后停止滚动，则时，，
故答案为：．
16．（2024·黑龙江绥化·中考真题）如图，已知，，，，，，，…，依此规律，则点的坐标为 ．
【答案】
【分析】本题考查了点坐标的规律探究．解题的关键在于根据题意推导出一般性规律．根据题意可知个点坐标的纵坐标为一个循环，的坐标为，据此可求得的坐标．
【详解】解：∵，，，，，，，…，，
∴可知个点坐标的纵坐标为一个循环，的坐标为，
∵，
∴的坐标为．
∴的坐标为
故答案为：．
17．（2024·黑龙江大兴安岭地·中考真题）如图，在平面直角坐标系中，正方形顶点M的坐标为，是等边三角形，点B坐标是，在正方形内部紧靠正方形的边（方向为）做无滑动滚动，第一次滚动后，点A的对应点记为，的坐标是；第二次滚动后，的对应点记为，的坐标是；第三次滚动后，的对应点记为，的坐标是；如此下去，……，则的坐标是 ．
【答案】
【分析】本题考查了点的坐标变化规律，正方形性质，等边三角形性质，根据三角形的运动方式，依次求出点A的对应点，，，的坐标，发现规律即可解决问题．
【详解】解：正方形顶点M的坐标为，
,
是等边三角形，点B坐标是，
等边三角形高为，
由题知，
的坐标是；
的坐标是；
的坐标是；
继续滚动有，的坐标是；
的坐标是；
的坐标是；
的坐标是；
的坐标是；
的坐标是；
的坐标是；
的坐标是；
的坐标是；
的坐标是；不断循环，循环规律为以，，，，12个为一组，
，
的坐标与的坐标一样为，
故答案为：．
18．（2024·山东泰安·中考真题）如图所示，是用图形“○”和“●”按一定规律摆成的“小屋子”．按照此规律继续摆下去，第 个“小屋子”中图形“○”个数是图形“●”个数的3倍．
【答案】12
【分析】本题主要考查了图形变化的规律、一元二次方程的应用等知识点，能根据所给图形发现“〇”和“●”的个数变化规律是解题的关键．
根据所给图形，依次求出“〇”和“●”的个数，发现规律，再利用规律列出一元二次方程求解即可．
【详解】解：由所给图形可知，
第1个“小屋子”中图形“〇”的个数为：，“●”的个数为：；
第2个“小屋子”中图形“〇”的个数为：，“●”的个数为：；
第3个“小屋子”中图形“〇”的个数为：，“●”的个数为：；
第4个“小屋子”中图形“〇”的个数为：，“●”的个数为：；
…，
所以第n个“小屋子”中图形“〇”的个数为：，“●”的个数为：；
由题知，解得，
又n为正整数，则，即第12个“小屋子”中图形“〇”个数是图形“●”个数的3倍．
故答案为：12．
19．（2024·四川遂宁·中考真题）在等边三边上分别取点，使得，连结三点得到，易得，设，则
如图①当时，
如图②当时，
如图③当时，
……
直接写出，当时， ．
【答案】/0.73
【分析】本题主要考查数字规律性问题，首先根据已知求得比例为n时，，代入即可．
【详解】解：根据题意可得，当时，，
则当时，，
故答案为：．
20．（2024·四川德阳·中考真题）数学活动课上，甲组同学给乙组同学出示了一个探究问题：把数字1至8分别填入如图的八个圆圈内，使得任意两个有线段相连的圆圈内的数字之差的绝对值不等于1．经过探究后，乙组的小高同学填出了图中两个中心圆圈的数字a、b，你认为a可以是 （填上一个数字即可）．
【答案】1/8
【分析】本题考查了数字规律，理解题意是解题的关键．由于两个中心圆圈有6根连线，数字1至8，共有8个数字，若2，3，4，5，6，7，其中任何一个数字填在中心位置，那么与其相邻的2个数字均不能出现在与中心圆圈相连的6个圆圈中，否则不满足任意两个有线段相连的圆圈内的数字之差的绝对值不等于1，故只剩下5个数字可选，不满足6个空的圆圈需要填入，故中心圆圈只能是1或者8．
【详解】解： 两个中心圆圈分别有6根连线，数字1至8，共有8个数字，若2，3，4，5，6，7，其中任何一个数字填在中心位置，那么与其相邻的2个数字均不能出现在与中心圆圈相连的6个圆圈中，故只剩下5个数字可选，不满足6个空的圆圈需要填入．
位于两个中心圆圈的数字a、b，只可能是1或者8．
故答案为：1（或8）．
21．（2024·四川成都·中考真题）在综合实践活动中，数学兴趣小组对这个自然数中，任取两数之和大于的取法种数进行了探究．发现：当时，只有一种取法，即；当时，有和两种取法，即；当时，可得；……．若，则的值为 ；若，则的值为 ．
【答案】 9 144
【分析】本题考查数字类规律探究，理解题意，能够从特殊到一般，得到当n为偶数或奇数时的不同取法是解答的关键．先根据前几个n值所对应k值，找到变化规律求解即可．
【详解】解：当时，只有一种取法，则；
当时，有和两种取法，则；
当时，有，，，四种取法，则；
故当时，有，，，，，六种取法，则；
当时，有，，，，，，，，九种取法，则；
依次类推，
当n为偶数时，，
故当时，，
故答案为：9，144．
22．（2024·四川广安·中考真题）已知，直线与轴相交于点，以为边作等边三角形，点在第一象限内，过点作轴的平行线与直线交于点，与轴交于点，以为边作等边三角形（点在点的上方），以同样的方式依次作等边三角形，等边三角形，则点的横坐标为 ．
【答案】
【分析】直线直线可知，点坐标为，可得，由于是等边三角形，可得点，把代入直线解析式即可求得的横坐标，可得，由于是等边三角形，可得点；同理，，发现规律即可得解，准确发现坐标与字母的序号之间的规律是解题的关键．
【详解】解：∵直线l：与x轴负半轴交于点，
∴点坐标为，
∴，
过，，作轴交x轴于点M，轴交于点D，交x轴于点N，

∵为等边三角形，
∴
∴，
∴
∴，
当时，，解得：，
∴，，
∴，
∴，
∴，
∴当时，，解得：，
∴；
而，
同理可得：的横坐标为，
∴点的横坐标为，
故答案为：．
【点睛】本题主要考查了一次函数图象上点的坐标的特征，勾股定理的应用，等边三角形的性质，特殊图形点的坐标的规律，掌握探究的方法是解本题的关键.
三、解答题
23．（2024·四川凉山·中考真题）阅读下面材料，并解决相关问题：
下图是一个三角点阵，从上向下数有无数多行，其中第一行有1个点，第二行有2个点……第行有个点……
容易发现，三角点阵中前4行的点数之和为10．
(1)探索：三角点阵中前8行的点数之和为_____，前15行的点数之和为______，那么，前行的点数之和为______
(2)体验：三角点阵中前行的点数之和______（填“能”或“不能”）为500．
(3)运用：某广场要摆放若干种造型的盆景，其中一种造型要用420盆同样规格的花，按照第一排2盆，第二排4盆，第三排6盆……第排盆的规律摆放而成，则一共能摆放多少排？
【答案】(1)36；120；
(2)不能
(3)一共能摆放20排．
【分析】本题考查了一元二次方程的应用，找准等量关系，正确列出一元二次方程是解题的关键．
（1）根据图形，总结规律，列式计算即可求解；
（2）根据前n行的点数和是500，即可得出关于n的一元二次方程，解之即可判断；
（2）先得到前n行的点数和是，再根据题意得出关于n的一元二次方程，解之即可得出n的值．
【详解】（1）解：三角点阵中前8行的点数之和为，
前15行的点数之和为，
那么，前行的点数之和为；
故答案为：36；120；；
（2）解：不能，
理由如下：
由题意得，
得，
，
∴此方程无正整数解，
所以三角点阵中前n行的点数和不能是500；
故答案为：不能；
（3）解：同理，前行的点数之和为，
由题意得，
得，即，
解得或（舍去），
∴一共能摆放20排．
24．（2024·江苏盐城·中考真题）发现问题
小明买菠萝时发现，通常情况下，销售员都是先削去菠萝的皮，再斜着铲去菠萝的籽．
提出问题
销售员斜着铲去菠萝的籽，除了方便操作，是否还蕴含着什么数学道理呢？
分析问题
某菠萝可以近似看成圆柱体，若忽略籽的体积和铲去果肉的厚度与宽度，那么籽在侧面展开图上可以看成点，每个点表示不同的籽．该菠萝的籽在侧面展开图上呈交错规律排列，每行有n个籽，每列有k个籽，行上相邻两籽、列上相邻两籽的间距都为d（n，k均为正整数，，），如图1所示．
小明设计了如下三种铲籽方案．
方案1：图2是横向铲籽示意图，每行铲的路径长为________，共铲________行，则铲除全部籽的路径总长为________；
方案2：图3是纵向铲籽示意图，则铲除全部籽的路径总长为________；
方案3：图4是销售员斜着铲籽示意图，写出该方案铲除全部籽的路径总长．
解决问题
在三个方案中，哪种方案铲籽路径总长最短？请写出比较过程，并对销售员的操作方法进行评价．
【答案】分析问题：方案1：；；；方案2：；方案3：；解决问题：方案3路径最短，理由见解析
【分析】分析问题：方案1：根据题意列出代数式即可求解；方案2：根据题意列出代数式即可求解；方案3：根据图得出斜着铲每两个点之间的距离为，根据题意得一共有列，行，斜着铲相当于有n条线段长，同时有个，即可得出总路径长；
解决问题：利用作差法比较三种方案即可．
题目主要考查列代数式，整式的加减运算，二次根式的应用，理解题意是解题关键．
【详解】解：方案1：根据题意每行有n个籽，行上相邻两籽的间距为d，
∴每行铲的路径长为，
∵每列有k个籽，呈交错规律排列，
∴相当于有行，
∴铲除全部籽的路径总长为，
故答案为：；；；
方案2：根据题意每列有k个籽，列上相邻两籽的间距为d，
∴每列铲的路径长为，
∵每行有n个籽，呈交错规律排列，，
∴相当于有列，
∴铲除全部籽的路径总长为，
故答案为：；
方案3：由图得斜着铲每两个点之间的距离为，
根据题意得一共有列，行，
斜着铲相当于有n条线段长，同时有个，
∴铲除全部籽的路径总长为：；
解决问题
由上得：，
∴方案1的路径总长大于方案2的路径总长；
，
∵，
当时，
，
，
∴方案3铲籽路径总长最短，销售员的操作方法是选择最短的路径，减少对菠萝的损耗．
例：“和点”按上述规则连续平移3次后，到达点，其平移过程如下：