初中数学中考复习专题满分秘籍将军饮马求最小值2-平移

这是一份初中数学中考复习专题满分秘籍将军饮马求最小值2-平移，共14页。试卷主要包含了开口向下，等内容，欢迎下载使用。

内容导航
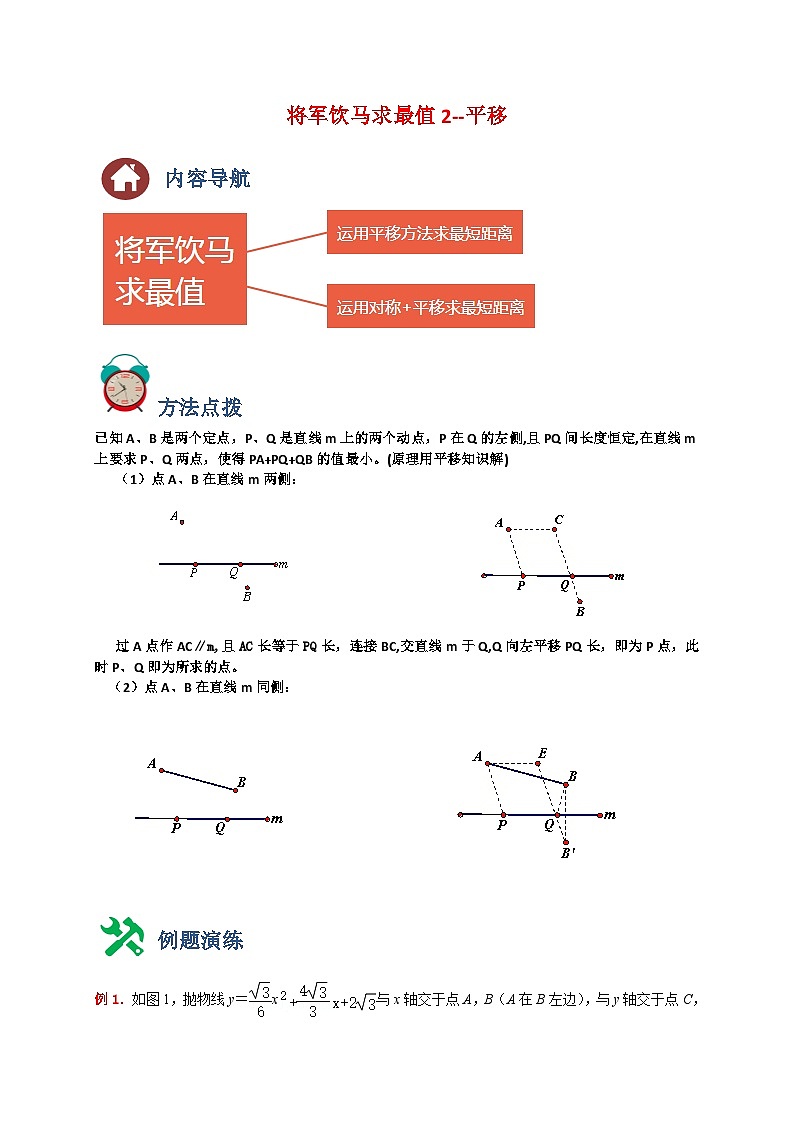
方法点拨
已知A、B是两个定点，P、Q是直线m上的两个动点，P在Q的左侧,且PQ间长度恒定,在直线m上要求P、Q两点，使得PA+PQ+QB的值最小。(原理用平移知识解)
（1）点A、B在直线m两侧：






过A点作AC∥m,且AC长等于PQ长，连接BC,交直线m于Q,Q向左平移PQ长，即为P点，此时P、Q即为所求的点。
（2）点A、B在直线m同侧：









例题演练

例1．如图1，抛物线y＝x与x轴交于点A，B（A在B左边），与y轴交于点C，连AC，点D与点C关于抛物线的对称轴对称，过点D作DE∥AC交抛物线于点E，交y轴于点P．
（1）点F是直线AC下方抛物线上点一动点，连DF交AC于点G，连EG，当△EFG的面积的最大值时，直线DE上有一动点M，直线AC上有一动点N，满足MN⊥AC，连GM，NO，求GM+MN+NO的最小值；
【解答】解：（1）如图1中，作FH∥y轴交DE于H．设F（m，m2+m+2）．
由题意可知A（﹣6，0），B（﹣2，0），C（0，2），
∵抛物线的对称轴x＝﹣4，C，D关于直线x＝﹣4对称，
∴D（﹣8，2），
∴直线AC的解析式为y＝x+2，
∵DE∥AC，
∴直线DE的解析式为y＝x+，
由，解得或，
∴E（2，），H（m，m+），
∵S△DEF＝S△DEG+S△EFG，△DEG的面积为定值，
∴△DEF的面积最大时，△EFG的面积最大，
∵FH的值最大时，△DEF的面积最大，
∴FH的值最大时，△EFG的面积最大，
∵FH＝﹣m2﹣m+，
∵a＜0．开口向下，
∴x＝﹣3时，FH的值最大，此时F（﹣3，﹣）．
如图2中，作点G关于DE 的对称点T，TG交DE于R，连接OR交AC于N，作NM⊥DE于M，连接TM，GM，此时GM+MN+ON的值最小．
∵直线DF的解析式为：y＝﹣x﹣2，
由，
解得，
∴G（﹣，），
∵TG⊥AC，
∴直线GR的解析式为y＝﹣x﹣，
由，解得，
∴R（﹣，），
∴RG＝4，OR＝，
∵GM＝TM＝RN，
∴GM+MN+ON＝RN+ON+RG＝RG+ON＝4+．
∴GM+MN+NO的最小值为4+．
练1.1如图1，已知抛物线y＝﹣x2+2x+3与x轴交于A、B两点，与y轴交于点C，顶点为D，连接BC
（1）点G是直线BC上方抛物线上一动点（不与B、C重合），过点G作y轴的平行线交直线BC于点E，作GF⊥BC于点F，点M、N是线段BC上两个动点，且MN＝EF，连接DM、GN．当△GEF的周长最大时，求DM+MN+NG的最小值；
【解答】解：（1）y＝﹣x2+2x+3＝﹣（x﹣3）（x+1）＝﹣（x﹣1）2+4
∴抛物线与x轴交于点A（﹣1，0）、点B（3，0），与y轴交于点C（0，3），顶点D（1，4），
∴直线CB解析式：y＝﹣x+3，∠BCO＝45°
∵GE∥y轴，GF⊥BC
∴∠GEF＝∠BCO＝45°，∠GFE＝90°
∴△GEF是等腰直角三角形，EF＝FG＝GE
∴C△GEF＝EF+FG+GE＝（+1）GE
设点G（a，﹣a2+2a+3），则点E（a，﹣a+3），其中0＜a＜3
∴GE＝﹣a2+2a+3﹣（﹣a+3）＝﹣a2+3a＝﹣（a﹣）2+
∴a＝时，GE有最大值为
∴△GEF的周长最大时，G（，），E（，），
∴MN＝EF＝，E点可看作点F向右平移个单位、向下平移个单位
如图1，作点D关于直线BC的对称点D1（﹣1，2），过N作ND2∥D1M且ND2＝D1M
∴DM＝D1M＝ND2，D2（﹣1+，2﹣）即D2（，）
∴DM+MN+NG＝MN+ND2+NG
∴当D2、N、G在同一直线上时，ND2+NG＝D2G为最小值
∵D2G＝
∴DM+MN+NG最小值为
练1.2如图，在平面直角坐标系中，抛物线y＝x2+2x﹣3与x轴交于A，B两点（点A在点B的左侧），与y轴交于点C，对称轴为直线l，点D（﹣4，n）在抛物线上．
（1）求直线CD的解析式；
（2）E为直线CD下方抛物线上的一点，连接EC，ED，当△ECD的面积最大时，在直线l上取一点M，过M作y轴的垂线，垂足为点N，连接EM，BN，若EM＝BN时，求EM+MN+BN的值．
【解答】解：（1）由题意C（0，﹣3），D（﹣4，5），
设直线CD的解析式为y＝kx+b，则有
解得，
∴直线CD的解析式为y＝﹣2x﹣3．
（2）如图1中，过点E作EG∥y轴交直线CD于G．设E（m，m2+2m﹣3）．则G（m，﹣2m﹣3），GE＝﹣m2﹣4m．
∴S△EDC＝•EG•|Dx|＝（﹣m2﹣4m）×4＝﹣2（m+2）2+8，
∵﹣2＜0，
∴m＝﹣2时，△DEC的面积最大，此时E（﹣2，﹣3），
∵C（0，﹣3），
∴EC∥AB，设CE交对称轴于H，
∵B（1，0），
∴EH＝OB＝1，∵EM＝BN，
∴Rt△EHM≌Rt△BON，
∴MH＝ON＝OC＝，
∴EM＝BN＝＝，
∴EM+MN+BN＝1+．
练1.3如图，在平面直角坐标系中，抛物线y＝﹣x2﹣x+b与x轴交于A、B两点（点A在点B左侧），与y轴交于点C，OB＝1，∠OBC＝60°．
（1）如图1，求直线BC的解析式；
（2）如图1，线段AC上方抛物线上有一动点P，PD⊥x轴于点H，交线段AC于点D，直线BG∥AC，交抛物线于点G，点F是直线BC上一动点，FE∥BC交AC于点E，点Q是点A关于直线BG的对称点，连接PE、QF．当线段PD取最大值时，求PE+EF+QF的最小值及点E的坐标；
【解答】解：（1）在△BOC 中，OB＝1，∠OBC＝60°
∴BC＝2，OC＝．
∴抛物线解析式为：；
令y＝0，得
解之得，x1﹣3，x2＝1
∴A（﹣3，0），B（1，0），C（0，）
设直线BC解析式为：y＝kx+b，经过B（1，0），C（0，）
∴，
∴，
∴；
（2）设直线AC解析式为：y＝k1x+b1，经过A（﹣3，0），B（1，0），得
设P点坐标为，则D点坐标为
∴PD＝═
当时，PD有最大值．
∴P点坐标为；
在R△AOC中，可以求出AC＝2，AB＝4
∴AC2+BC2＝12+4＝16＝AB2
由勾股定理逆定理得，可得∠ACB＝90°，
可得∠CAB＝30°＝∠ABG，
由对称可得，AB＝BQ＝4，∠ABQ＝30°+30°＝60°，
∴△ABQ 是等边三角形．
过点Q作QM⊥x轴于点M．
∴MB＝4，且OB＝1
∴OM＝1，QM＝2
∴Q点坐标为（﹣1，﹣2）；
由题意得，四边形BCEF是矩形，可得EF＝BC＝2．
将Q点沿射线EF方向平移2个单位（向左平移1个单位，向上平移个单位），可得Q′的坐标为（﹣2，﹣），
连接P Q′交AC于点E，点E即为所求．
P Q′＝
PE+EF+QF最小值＝P Q′+EF＝+2，
直线P Q的解析式为：
联立，
解得：x＝﹣，故E点坐标；
练1.4如图1，在平面直角坐标系中，抛物线y＝﹣x2+2x﹣与x轴交于A、B两点（点A在点B的左侧），与y轴交于点C，顶点为D，对称轴与x轴交于点E，直线CE交抛物线于点F（异于点C），直线CD交x轴交于点G．
（1）如图1，求直线CE的解析式和顶点D的坐标；
（2）如图1，点P为直线CF上方抛物线上一点，连接PC、PF，当△PCF的面积最大时，点M是过P垂直于x轴的直线l上一点，点N是抛物线对称轴上一点，求FM+MN+NO的最小值；
【解答】解：（1）∵抛物线y＝﹣x2+2x﹣与y轴交于点C，
∴C（0，﹣），
∵y＝﹣x2+2x﹣＝﹣（x﹣2）2+，
∴顶点D（2，），对称轴x＝2，
∴E（2，0），
设CE解析式y＝kx+b，
∴，
解得：，
∴直线CE的解析式：y＝x﹣；
（2）∵直线CE交抛物线于点F（异于点C），
∴x﹣＝﹣（x﹣2）2+，
∴x1＝0，x2＝3，
∴F（3，），
过P作PH⊥x轴，交CE于H，如图1，
设P（a，﹣a2+2a﹣） 则H（a，a﹣），
∴PH＝﹣a2+2a﹣﹣（a﹣），
＝﹣a2+，
∵S△CFP＝PH×3＝﹣a2+，
∴当a＝时，S△CFP面积最大，
如图2，作点M关于对称轴的对称点M'，过F点作FG∥MM'，FG＝1，即G（4，），
∵M的横坐标为，且M与M'关于对称轴x＝2对称，
∴M'的横坐标为，
∴MM'＝1，
∴MM'＝FG，且FG∥MM'，
∴FGM'M是平行四边形，
∴FM＝GM'，
∴FM+MN+ON＝GM'+NM'+ON，
根据两点之间线段最短可知：当O，N，M'，G四点共线时，GM'+NM'+ON的值最短，即 FM+MN+ON的值最小，
∴FM+MN+ON＝OG＝＝；
练1.5如图所示，在平面直角坐标系中，Rt△AOB的顶点坐标分别为A（﹣2，0），O（0，0），B（0，4），把△AOB绕点O按顺时针方向旋转90°，得到△COD．
（1）求C、D两点的坐标；
（2）求经过A、B、D三点的抛物线的解析式；
（3）在（2）中抛物线的对称轴上取两点E、F（点E在点F的上方），且EF＝1，使四边形ACEF的周长最小，求出E、F两点的坐标．
【解答】解：（1）由旋转的性质可知：OC＝OA＝2，OD＝OB＝4
∴C点的坐标是（0，2），D点的坐标是（4，0），

（2）设所求抛物线的解析式为y＝ax2+bx+c，
由题意，得，
解得，b＝1，c＝4，
∴所求抛物线的解析式为；

（3）只需求AF+CE最短，
抛物线的对称轴为x＝1，
将点A向上平移至A1（﹣2，1），则AF＝A1E，
作A1关于对称轴x＝1的对称点A2（4，1），
连接A2C，A2C与对称轴交于点E，E为所求，
可求得A2C的解析式为，
当x＝1时，，
∴点E的坐标为，点F的坐标为．
练1.6如图1，已知抛物线y＝x2+2x﹣3与x轴相交于A，B两点，与y轴交于点C，D为顶点．
（1）求直线AC的解析式和顶点D的坐标；
（2）已知E（0，），点P是直线AC下方的抛物线上一动点，作PR⊥AC于点R，当PR最大时，有一条长为的线段MN（点M在点N的左侧）在直线BE上移动，首尾顺次连接A、M、N、P构成四边形AMNP，请求出四边形AMNP的周长最小时点N的坐标；
【解答】解：（1）对于抛物线y＝x2+2x﹣3，令y＝0，得x2+2x﹣3＝0，解得x＝﹣3或1，
∴A（﹣3，0），B（1，0），
令x＝0，得y＝﹣3，
∴C（0，﹣3），
∵抛物线y＝x2+2x﹣3＝（x+1）2﹣4，
∴顶点D坐标为（﹣1，﹣4），
设直线AC的解析式为y＝kx+b，则有，解得，
∴直线AC的解析式为y＝﹣x﹣3，点D坐标（﹣1，﹣4）．

（2）如图1中，设P（m，m2+2m﹣3），
由题意，当PR最大时，△ACP的面积最大，即四边形APCO的面积最大，
∵S四边形APCO＝S△AOP+S△POC﹣S△AOC＝•3•（﹣m2﹣2m+3）+•3•（﹣m）﹣•3•3＝﹣m2﹣m＝﹣（m+）2+，
∴当m＝﹣时，四边形APCO的面积最大，即PR最长，
∴P（﹣，﹣），
将点P沿BE方向平移个单位得到G（﹣，﹣），作点A关于直线BE的对称点K，连接GK交BE于M，此时四边形APNM的最长最小，
∵直线BE的解析式为y＝﹣x+，直线AK的解析式为y＝2x+6，
由解得，
∴J（﹣，），
∵AJ＝JK，
∴k（﹣，），
∴直线KG的解析式为y＝x+，
由解得，
∴M（﹣2，），将点M向下平移1个单位，向右平移2个单位得到N，
∴N（0，）．