2024年高考数学二轮复习讲练测（新教材新高考）专题15立体几何解答题归类含解析答案

这是一份2024年高考数学二轮复习讲练测（新教材新高考）专题15立体几何解答题归类含解析答案，共73页。试卷主要包含了解答题等内容，欢迎下载使用。

一、解答题
1．如图，四面体中，，平面．
(1)求证：平面；
(2)求二面角的大小．
2．如图，在三棱台中，平面，为中点.，N为AB的中点，

(1)求证：//平面；
(2)求平面与平面所成夹角的余弦值；
(3)求点到平面的距离．
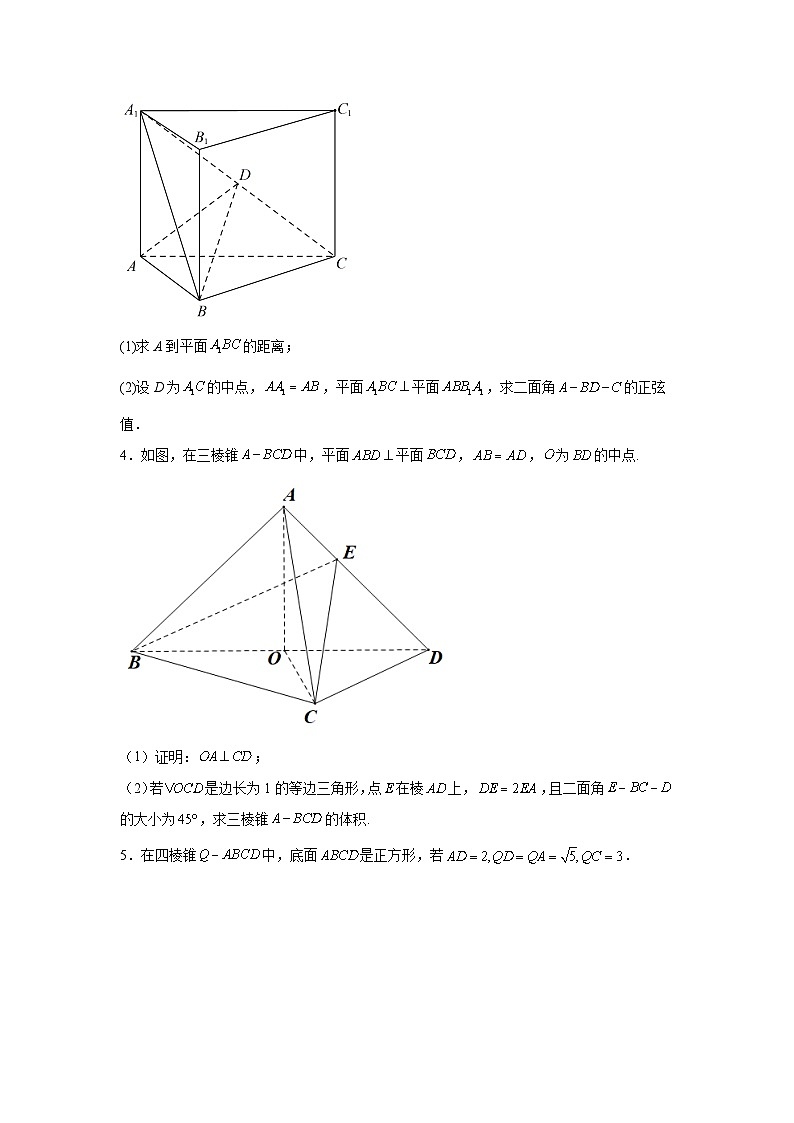
3．如图，直三棱柱的体积为4，的面积为．
(1)求A到平面的距离；
(2)设D为的中点，，平面平面，求二面角的正弦值．
4．如图，在三棱锥中，平面平面，，为的中点.
（1）证明：；
（2）若是边长为1的等边三角形，点在棱上，，且二面角的大小为，求三棱锥的体积.
5．在四棱锥中，底面是正方形，若．
（1）证明：平面平面；
（2）求二面角的平面角的余弦值．
6．如图，在三棱锥中，，，，，的中点分别为，点在上，．
(1)求证：//平面；
(2)若，求三棱锥的体积．
7．如图，四面体中，，E为AC的中点．
(1)证明：平面平面ACD；
(2)设，点F在BD上，当的面积最小时，求三棱锥的体积．
8．如图，在圆锥中，是底面的直径，且，，，是的中点．

(1)求证：平面平面；
(2)求二面角的余弦值．
9．如图，圆台的轴截面为等腰梯形，为底面圆周上异于的点.

(1)在平面内，过作一条直线与平面平行，并说明理由；
(2)若四棱锥的体积为，设平面平面，求的最小值.
10．如图，已知四棱台的上、下底面分别是边长为2和4的正方形， ，且底面，点分别在棱、上·
(1)若P是的中点，证明：；
(2)若平面，且平面PQD与平面AQD的夹角的余弦值为，求四面体的体积．
11．等边三角形的边长为3，点分别是边上的点，且满足，如图甲，将沿折起到的位置，使二面角为直二面角，连接，如图乙.

(1)求证：平面.
(2)在线段上是否存在点，使平面与平面所成的角为？若存在，求出的长；若不存在，请说明理由.
12．如图，在棱长为2的正方体中，为棱的中点，为棱上一点.
(1)求直线与平面所成角的正弦值；
(2)求二面角的正弦值；
(3)是否存在点，使平面？若存在，求出的长度；若不存在，请说明理由.
13．如图，在三棱台中，若平面，为中点，为棱上一动点（不包含端点）.
(1)若为的中点，求证：平面.
(2)是否存在点，使得平面与平面所成角的余弦值为？若存在，求出长度；若不存在，请说明理由.
14．如图，在菱形中，，，将沿着翻折，形成三棱锥.
(1)当时，证明：；
(2)当平面平面时，求直线与平面所成角的余弦值.
15．如图1所示，四边形ABCD中，，，，，M为AD的中点，N为BC上一点，且．现将四边形ABNM沿MN翻折，使得AB与EF重合，得到如图2所示的几何体MDCNFE，其中．

(1)证明：平面FND；
(2)若P为FC的中点，求二面角的正弦值．
16．在（图1）中，为边上的高，且满足，现将沿翻折得到三棱锥（图2），使得二面角为.

(1)证明：平面；
(2)在三棱锥中，为棱的中点，点在棱上，且，若点到平面的距离为，求的值.
17．如图，三棱柱中，侧面为菱形.

(1)（如图1）若点为内任一点，作出与面的交点（作出图象并写出简单的作图过程，不需证明）；
(2)（如图2）若面面，求二面角的余弦值.
18．如图，已知多面体EABCDF的底面ABCD是边长为2的正方形，，，且.

(1)记线段的中点为，在平面内过点作一条直线与平面平行，要求保留作图痕迹，但不要求证明；
(2)求直线与平面所成角的正弦值.
19．已知四棱锥中，底面为直角梯形，平面，，，，，M为中点，过C，D，M的平面截四棱锥所得的截面为．
(1)若与棱交于点F，画出截面，保留作图痕迹（不用说明理由），求点F的位置；
(2)求平面与平面所成锐二面角的余弦值．
20．如图，已知三棱柱的底面是正三角形，侧面是矩形，，分别为，的中点，为上一点，过 和的平面交于，交于.
（1）证明：，且平面平面；
（2）设为的中心，若，平面，且，求四棱锥的体积.
21．如图，已知三棱柱的底面是正三角形，侧面是矩形，M，N分别为BC，的中点，P为AM上一点，过和P的平面交AB于E，交AC于F.
（1）证明：，且平面；
（2）设O为的中心，若面，且，求直线与平面所成角的正弦值.
22．在三棱柱中，，平面，、分别是棱、的中点.
(1)设为的中点，求证：平面；
(2)若，直线与平面所成角的正切值为，求多面体的体积.
23．《九章算术》是中国古代的一部数学专著，是《算经十书》中最重要的一部，成于公元一世纪左右.它是一本综合性的历史著作，是当时世界上最简练有效的应用数学，它的出现标志着中国古代数学形成了完整的体系.《九章算术》中将由四个直角三角形组成的四面体称为“鳖臑”，已知在三棱锥中，平面.

（1）从三棱锥中选择合适的两条棱填空：________________，则三棱锥为“鳖臑”；
（2）如图，已知，垂足为，，垂足为，.
（i）证明：平面平面；
（ii）设平面与平面交线为，若，，求二面角的大小.
24．如图，四棱锥中，底面为边长是2的正方形，，分别是，的中点，，，且二面角的大小为.
(1) 求证：；
(2) 求二面角的余弦值.
25．如图，四棱锥中，四边形是边长为2的菱形，
（1）证明：平面平面；
（2）当平面与平面所成锐二面角的余弦值，求直线与平面所成角正弦值.
26．如图，在四面体中，已知，，
(1)求证：；
(2)若平面平面，且，求二面角的余弦值.
27．如图，P为圆锥的顶点，O是圆锥底面的圆心，为底面直径，为底面圆O的内接正三角形，点E在母线上，且，.
(1)求证：平面平面；
(2)若点M为线段上的动点，当直线与平面所成角的正弦值最大时，求此时点到平面的距离.
28．如图，在斜三棱柱中，是边长为2的正三角形，且四棱锥的体积为2.
(1)求三棱柱的高；
(2)若，平面平面为锐角，求平面与平面的夹角的余弦值.
29．如图，四棱锥中，侧面为等边三角形，线段的中点为且底面，，，是的中点.
(1)证明：平面；
(2)求点到平面的距离；
(3)点在棱上，且直线与底面所成角的正弦值为，求平面与平面夹角的余弦值.
30．已知底面为正三角形的斜三棱柱中，分别是棱，的中点，点在底面投影为边的中点，，.
（1）证明：//平面；
（2）若，，点为棱上的动点，当直线与平面所成角的正弦值为时，求点的位置.
31．如图，在三棱台中，，，为的中点，二面角的大小为.
（1）证明：；
（2）当为何值时，直线与平面所成角的正弦值为？
32．已知三棱台的体积为，且，平面.
(1)证明：平面平面；
(2)若，，求二面角的正弦值.
33．如图，在四棱锥中，，，与均为正三角形.

(1)证明：平面.
(2)证明：平面.
(3)设平面平面，平面平面，若直线与确定的平面为平面，线段的中点为，求点到平面的距离.
34．已知，，，定义一种运算：，在平行六面体中，，，.
(1)证明：平行六面体是直四棱柱；
(2)计算，并求该平行六面体的体积，说明的值与平行六面体体积的关系.
35．（1）在空间直角坐标系中，已知平面的法向量，且平面经过点，设点是平面内任意一点.求证：.
（2）我们称（1）中结论为平面的点法式方程，若平面过点，求平面的点法式方程.
36．北京大兴国际机场的显著特点之一是各种弯曲空间的运用．刻画空间的弯曲性是几何研究的重要内容．用曲率刻画空间弯曲性，规定：多面体顶点的曲率等于与多面体在该点的面角之和的差（多面体的面的内角叫做多面体的面角，角度用弧度制），多面体面上非顶点的曲率均为零，多面体的总曲率等于该多面体各顶点的曲率之和．例如：正四面体在每个顶点有3个面角，每个面角是，所以正四面体在各顶点的曲率为，故其总曲率为．

（1）求四棱锥的总曲率；
（2）若多面体满足：顶点数-棱数+面数，证明：这类多面体的总曲率是常数．
参考答案：
1．(1)证明见解析；
(2)．
【分析】（1）由平面，可得，由勾股定理可得，再利用线面垂直的判定定理即可证得平面；
（2）以点B为坐标原点，分别以所在直线为x轴，y轴的正方向，建立空间直角坐标系，求出相应向量的坐标，进而求出平面和平面的法向量，再利用二面角的向量公式计算即可．
【详解】（1）∵平面，平面，平面，
∴，
∵，
∴，
又∵，∴，
∴，又∵，平面，
∴平面；
（2）以点B为坐标原点，分别以所在直线为x轴，y轴的正方向，建立空间直角坐标系，如图所示：
则，
∴，
设平面的一个法向量为，
则，取，得，
设平面的一个法向量为，
则，取，得，
∴，
由图可知二面角为锐角，设二面角的大小为，
则，而，
∴．
即二面角的大小为．
2．(1)证明见解析
(2)
(3)
【分析】（1）先证明四边形是平行四边形，然后用线面平行的判定解决；
（2）利用二面角的定义，作出二面角的平面角后进行求解；
（3）方法一是利用线面垂直的关系，找到垂线段的长，方法二无需找垂线段长，直接利用等体积法求解
【详解】（1）

连接.由分别是的中点，根据中位线性质，//，且，
由棱台性质，//，于是//，由可知，四边形是平行四边形，则//，
又平面，平面，于是//平面.
（2）过作，垂足为，过作，垂足为,连接.
由面，面，故，又，，平面，则平面.
由平面，故，又，，平面，于是平面，
由平面，故.于是平面与平面所成角即.
又，，则，故，在中，，则，
于是
（3）[方法一：几何法]

过作，垂足为，作，垂足为，连接，过作，垂足为.
由题干数据可得，，，根据勾股定理，，
由平面，平面，则，又，，平面，于是平面.
又平面，则，又，，平面，故平面.
在中，，
又，故点到平面的距离是到平面的距离的两倍，
即点到平面的距离是.
[方法二：等体积法]

辅助线同方法一.
设点到平面的距离为.
，
.
由，即.
3．(1)
(2)
【分析】（1）由等体积法运算即可得解；
（2）由面面垂直的性质及判定可得平面，建立空间直角坐标系，利用空间向量法即可得解.
【详解】（1）在直三棱柱中，设点A到平面的距离为h，
则，
解得，
所以点A到平面的距离为；
（2）取的中点E,连接AE,如图，因为，所以,
又平面平面，平面平面，
且平面，所以平面，
在直三棱柱中，平面，
由平面，平面可得，，
又平面且相交，所以平面，
所以两两垂直，以B为原点，建立空间直角坐标系，如图，
由（1）得，所以，，所以，
则,所以的中点，
则，,
设平面的一个法向量，则，
可取，
设平面的一个法向量，则，
可取，
则，
所以二面角的正弦值为.
4．(1)证明见解析；(2).
【分析】(1)由题意首先证得线面垂直，然后利用线面垂直的定义证明线线垂直即可；
(2)方法二：利用几何关系找到二面角的平面角，然后结合相关的几何特征计算三棱锥的体积即可.
【详解】（1）因为，O是中点，所以，
因为平面，平面平面，
且平面平面，所以平面．
因为平面，所以.
（2）[方法一]：通性通法—坐标法
如图所示，以O为坐标原点，为轴，为y轴，垂直且过O的直线为x轴，建立空间直角坐标系，
则，设,
所以，
设为平面的法向量，
则由可求得平面的一个法向量为．
又平面的一个法向量为，
所以，解得．
又点C到平面的距离为，所以，
所以三棱锥的体积为．
[方法二]【最优解】：作出二面角的平面角
如图所示，作，垂足为点G．
作，垂足为点F，连结，则．
因为平面，所以平面，
为二面角的平面角．
因为，所以．
由已知得，故．
又，所以．
因为，
．
[方法三]：三面角公式
考虑三面角，记为，为，，
记二面角为．据题意，得．
对使用三面角的余弦公式，可得，
化简可得．①
使用三面角的正弦公式，可得，化简可得．②
将①②两式平方后相加，可得，
由此得，从而可得．
如图可知，即有，
根据三角形相似知，点G为的三等分点，即可得，
结合的正切值，
可得从而可得三棱锥的体积为．
【整体点评】(2)方法一：建立空间直角坐标系是解析几何中常用的方法，是此类题的通性通法，其好处在于将几何问题代数化，适合于复杂图形的处理；
方法二：找到二面角的平面角是立体几何的基本功，在找出二面角的同时可以对几何体的几何特征有更加深刻的认识，该法为本题的最优解.
方法三：三面角公式是一个优美的公式，在很多题目的解析中灵活使用三面角公式可以使得问题更加简单、直观、迅速.
5．（1）证明见解析；（2）.
【分析】（1）取的中点为，连接，可证平面，从而得到面面.
（2）在平面内，过作，交于，则，建如图所示的空间坐标系，求出平面、平面的法向量后可求二面角的余弦值.
【详解】
（1）取的中点为，连接.
因为，，则，
而，故.
在正方形中，因为，故，故，
因为，故，故为直角三角形且，
因为，故平面，
因为平面，故平面平面.
（2）在平面内，过作，交于，则，
结合（1）中的平面，故可建如图所示的空间坐标系.
则，故.
设平面的法向量，
则即，取，则，
故.
而平面的法向量为，故.
二面角的平面角为锐角，故其余弦值为.
6．(1)证明见解析
(2)
【分析】（1）根据给定条件，证明四边形为平行四边形，再利用线面平行的判定推理作答.
（2）作出并证明为棱锥的高，利用三棱锥的体积公式直接可求体积.
【详解】（1）连接，设，则，，，
则，
解得，则为的中点，由分别为的中点，
于是，即，
则四边形为平行四边形，
，又平面平面，
所以平面.
（2）过作垂直的延长线交于点，
因为是中点，所以，
在中，，
所以，
因为，
所以，又，平面，
所以平面，又平面，
所以，又，平面，
所以平面，
即三棱锥的高为，
因为，所以，
所以，
又，
所以.
7．(1)证明详见解析
(2)
【分析】（1）通过证明平面来证得平面平面.
（2）首先判断出三角形的面积最小时点的位置，然后求得到平面的距离，从而求得三棱锥的体积.
【详解】（1）由于，是的中点，所以.
由于，所以，
所以，故，
由于，平面，
所以平面，
由于平面，所以平面平面.
（2）[方法一]：判别几何关系
依题意，，三角形是等边三角形，
所以，
由于，所以三角形是等腰直角三角形，所以.
，所以，
由于，平面，所以平面.
由于，所以，
由于，所以，
所以，所以，
由于，所以当最短时，三角形的面积最小
过作，垂足为，
在中，，解得，
所以，
所以
过作，垂足为，则，所以平面，且，
所以，
所以.
[方法二]：等体积转换
，，
是边长为2的等边三角形，
连接
8．(1)证明见解析
(2)
【分析】（1）由已知证明，，可得平面，即可得到平面平面；
（2）在平面中，过作，垂足为，在平面中，过作，垂足为，连接，可得为二面角的平面角，再由已知求解三角形得答案．
【详解】（1）如图，由题意，是底面的直径，，
为的中点，为的中点，则，
则，而平面平面，
则，
又，平面，平面
平面，
又平面平面平面；
（2）在平面中，过作，垂足为，
在平面中，过作，垂足为，
连接，
∵平面平面，，
又，平面，平面，
平面，平面，，
，平面，平面
则平面，可得为二面角的平面角．
由已知可得，，，
，，
，
又，得．
在中，，
∴．
即二面角的余弦值为．

9．(1)作图见解析，理由见解析
(2)
【分析】(1)根据线面平行的判定和中位线定理即可求解;
(2)根据几何关系或空间向量方法即可求解.
【详解】（1）取中点，作直线即为所求，
取中点，连接，
则有，
如图，在等腰梯形中，，
有，
则四边形为平行四边形，

即有，
又平面平面，
所以平面.
（2）法一：延长交于点，
故平面平面
故平面平面即在中，均为圆锥母线.

过点作于.
在等腰梯形中，，
此梯形的高
等腰梯形的面积为，
所以四棱锥的体积，
解得，
故点与重合，
由，
得，且，
故.
中，到距离.
则面积,
得：的最小值为：.
法二：同法一求出的位置.
以为原点，方向为轴正向建立空间直角坐标系，
设面的法向量为
，
取，
有；
同理可得面的法向量为,
由面面，可知，
设的方向向量为，
故
取,
下面分2个方法求
求方法1：，
，
当时，取最小值为.
求方法2：在上的投影向量的模为
故的最小值即到的距离为.
法三:
在三角形中，
,
,
所以.
10．(1)证明见解析
(2)
【分析】（1）建立空间直角坐标系，利用空间向量的坐标运算知，即可证得结论；
（2）利用空间向量结合已知的面面角余弦值可求得，再利用线面平行的已知条件求得，再将四面体视为以为底面的三棱锥，利用锥体的体积公式即可得解.
【详解】（1）以为坐标原点，，，所在直线分别为，，轴建立空间直角坐标系，
则，，，，
设，其中，，
若是的中点，则，，，
于是，∴，即．
（2）由题设知，，，是平面内的两个不共线向量．
设是平面的一个法向量，
则，取，得．
又平面的一个法向量是，
∴，
而二面角的余弦值为，因此，
解得或（舍去），此时．
设，而，由此得点，，
∵PQ∥平面，且平面的一个法向量是，
∴，即，解得，从而．
将四面体视为以为底面的三棱锥，则其高，
故四面体的体积．
11．(1)证明见解析
(2)存在，
【分析】（1）由余弦定理求出，勾股定理可得，再由面面垂直的性质定理可得答案；
（2）假设在线段上存在点，使平面与平面所成的角为，以为原点，所在的直线分别为轴建立空间直角坐标系， 设，求出点坐标，求出平面、平面的法向量，再由二面角的向量求法可得，从而求出答案.
【详解】（1）因为等边三角形的边长为3，，所以，
在中，由余弦定理可得
，所以，可得，即
因为平面平面，平面平面，平面，
所以平面；
（2）假设在线段上存在点，使平面与平面所成的角为，
由（1）可知互相垂直，
以为原点，所在的直线分别为轴建立空间直角坐标系，
所以，，，，，
，，，
设，可得，，
设为平面的一个法向量，
所以，即，
令，则，
所以，因为平面，
所以可以为平面的一个法向量，
因为平面与平面所成的角为，
所以，
解得，所以存在点，且，
可得，，
.

12．(1)
(2)
(3)存在，
【分析】（1）首先以点为原点，建立空间直角坐标系，并求平面的法向量，利用向量法求线面角；
（2）根据（1）的结果，再根据向量法求二面角的余弦值，最后转化为正弦值，即可求解；
（3）根据（1）的结果，并设点的坐标为，若假设存在，则，即可求解.
【详解】（1）以为原点，，，分别为，，轴，建立如图空间直角坐标系，
则，，，，
，，，
，，
设平面的一个法向量为
，不妨设，则，，，
所以平面的一个法向量为
设直线与平面所成角为，
则.
（2）由正方体可得，，，且，
且平面，所以平面的一个法向量为，
则.
因为二面角为锐二面角，
所以二面角的正弦值为.
（3）存在，设点的坐标为，所以
平面的一个法向量为，
因为，所以，
因为平面，所以平面.
此时
13．(1)证明见详解
(2)存在，
【分析】（1）取中点，易征得四边形为平行四边形，得到，由线面平行的判定定理证明即可；
（2）以为坐标原点建立空间直角坐标系，设，根据面面角的向量求法可构造方程求得的值，由此可得结果.
【详解】（1）取中点，连接，
则为的中位线，所以,且，
又,
所以四边形为平行四边形，
则,又平面，平面，
所以平面.
（2）以为坐标原点，所在的直线为轴，
建立如图所示空间直角坐标系，
则,
则
设,则，
所以,
令平面的法向量为，
则，
令，则，，
又平面的一个法向量，
所以，
解得或者（舍），
所以
即的长度为
14．(1)证明见解析
(2)
【分析】（1）翻折后为正四面体，若证明线线垂直，可以先利用线面垂直的判定定理证明线面垂直，然后证明线面垂直即可.
（2）根据平面平面，可以建立空间直角坐标系，根据直线与平面的夹角的正弦是直线与平面法向量夹角的余弦的绝对值，求出线面角的正弦，然后求线面角的余弦即可.
【详解】（1）证明：当时，此三棱锥为正四面体，
如图，取的中点，连接，.
在正四面体中，，且，
且平面
所以平面，因为平面
所以
（2）解：当平面平面时，
取的中点，建立如图所示的空间直角坐标系，
则，，，.
设平面的法向量，，，
所以，即：，
令，得：
∴设直线与平面所成角为，且，
则，
∴，
∴直线与平面所成角的余弦值为.
15．(1)证明见解析
(2)
【分析】（1）先根据勾股定理的逆定理得到，再根据线面垂直的判定定理和性质得到，并且利用勾股定理的逆定理得到，最后利用线面垂直的判定定理证得平面FND；
（2）先建立合适的空间直角坐标系，再写出相关点及向量的坐标，最后利用向量的夹角公式和同角三角函数的基本关系求得结果．
【详解】（1）∵四边形ABCD中，，，，，
M为AD的中点，且，
∴四边形ABNM为正方形，且边长为1，
∴题图2中，四边形EMNF是边长为1的正方形，故，
又，，∴，∴，
又，，平面MDCN，平面MDCN，
∴平面MDCN，∵平面MDCN，∴，
易知，∴，∴，
又，平面，平面，
∴平面；
（2）解法一：由（1）知平面MDCN，又，
以N为坐标原点，建立空间直角坐标系，如图所示，

则，，，，
∴，，，
设平面FND的法向量为，则，
令，令，则，∴，
设平面PND的法向量为，则，
令，则，，∴，
∴，
∴，
∴二面角的正弦值为．
解法二：如图，取NC的中点O，连接PO，则，
∴平面MDCN，
∵平面MDCN，∴，
过O作，垂足为H，连接PH，则就是二面角的平面角，

又，，∴，∴，
∵平面MDCN，平面FND，∴平面平面MDCN，
∴二面角的正弦值为．
16．(1)证明见解析；
(2).
【分析】（1）由二面角定义确定为二面角的平面角，即，根据线面垂直的判定和性质证，再由已知证，最后根据线面垂直的判定证结论；
（2）构建空间直角坐标系，向量法求点面距离得到关于的方程，即可求值.
【详解】（1）在题图2中，则为二面角的平面角，即，
又，面，所以平面，
由平面，所以，
题图1中及，所以，
在中，由余弦定理得，
又，所以.
又，面，所以平面.
（2）以为坐标原点，以、、（）为、、轴，建立如图所示的空间直角坐标系.

在中，所以.
所以，
则，令，则，
由，则，
所以且，，，
设平面的法向量为，则，
取，所以，而
所以，解得或（舍去），故.
17．(1)答案见解析
(2)
【分析】（1）由平面的基本性质找两平面的交线，即可求得与面的交点；
（2）连接，，设，连接，证明、、两两垂直，以为坐标原点，分别以、、所在直线为、、轴，建立空间直角坐标系，设，再由空间向量求二面角的余弦值．
【详解】（1）
作图步骤
①连接并延长交于点
②连接交于点，连接
③连接交于点
④点即为所求.
（2）连结，交于点，连结，
侧面为菱形，，且为的中点，
，，
平面平面，平面平面，平面，
平面，
又，平面，，，
以为坐标原点，分别以、、所在直线为、、轴，建立空间直角坐标系，

设，则，0，，，0，，
，，，，，，
，，，
设平面与平面的一个法向量分别为与，
由，取，得；
由，取，得．
，
18．(1)答案见解析
(2)
【分析】（1）根据线面平行性质定理，可得所作直线必平行面与面的交线，因此先作两平面交线，再在平面内作交线的平行线.
（2）建立空间直角坐标系，求直线的方向向量和平面的法向量，利用向量夹角公式求直线与平面所成角的正弦值.
【详解】（1）延长，设其交点为，连接，
则为平面与平面的交线，
取线段CD的中点M，连接KM，直线KM即为所求．
证明如下：延长，设其交点为，连接，
则为平面与平面的交线，
因为，所以，又，
所以，
所以，又，
所以四边形为平行四边形，所以，
取的中点，连接，
∵分别为的中点，
∴，∴．
∵平面， 平面，
∴平面．

（2）以点为原点，所在的直线为轴，所在的直线为轴，建立空间直角坐标系，如图.由已知可得，
所以，
设平面的法向量为，
则得，
取得，，
平面的一个法向量.
设直线与平面所成的角为，
则.
所以直线与平面所成角的正弦值为.

19．(1)作图见解析；F为棱上靠近点B位置的三等分点；
(2).
【详解】（1）延长，连接交于F，连接，
如图，四边形为截面.
中，，由，则C为中点，B为中点，
过M作交于N，则，，
，
，即，
F为棱上靠近点B位置的三等分点；
（2）以A为原点，为x轴，为y轴，为z轴，建立空间坐标系如图，
则有：，，，，，
设平面的一个法向量为，，
则有，解得
令，则，即
设平面的一个法向量为，，，
则，解得，
令，则，，
设平面与平面的锐二面角的平面角为，则
所以平面与平面的二面角的锐平面角的余弦值为
20．（1）证明见解析；（2）192.
【分析】（1）由、可证；通过证明，平面，可证平面，从而可证平面平面；
（2）过作垂线，垂足为，利用可求出结果.
【详解】（1）因为，分别为，的中点，所以，
又，所以，
在等边中，为中点，则.
又因为侧面为矩形，所以.
因为，，
由，平面，
所以平面，
又因为，且平面，平面，
所以平面，
又因为平面，且平面平面，
所以.
又因为平面，
所以平面，
因为平面
所以平面平面.
（2）过作垂线，垂足为，画出图形，如图.
因为平面，平面，平面平面，
所以，
又因为，所以四边形为平行四边形，
所以，
因为为的中心，
所以，
因为平面平面，平面平面=，
平面，
所以平面，
又因为在等边中，，得，
由（1）知，四边形为梯形，
所以四边形的面积为，
所以， ，
，所以，
所以.
【点睛】关键点点睛：（1）中，利用直线与平面垂直证明平面与平面垂直是解题关键；（2）中，作出四棱锥的高，利用四棱锥的体积公式求解是解题关键.
21．（1）答案见解析；（2）
【分析】（1）推导出，四边形为矩形，，从而，由此能证明，又，即可得到平面．
（2）推导出，从而，四边形为平行四边形，，，，直线在平面内的投影为，从而直线与平面所成角即为等腰梯形中与所成角，由此能求出直线与平面所成角的正弦值．
【详解】解：（1）证明：，分别为，的中点，底面为正三角形，四边形是矩形，
，，四边形为矩形，，
，，，
，，，平面
平面，
综上，，且平面．
（2）解：三棱柱上下底面平行，平面与上下底面分别交于，，
，
面，面，面面，
，四边形为平行四边形，
是正三角形的中心，，
，，，
由（1）知直线在平面内的投影为，
直线与平面所成角即为等腰梯形中与所成角，
在等腰梯形中，令，过作于，
则，，，，
直线与平面所成角的正弦值为．
22．(1)证明见解析
(2)
【分析】
（1）作出辅助线，证明得到线线平行，从而证明线面平行；
（2）证明线面垂直，得到即是直线与平面所成的角，根据正切值为，得到，证明出平面，得到各边长，求出，结合多面体为四棱锥，且四边形是平行四边形求出多面体的体积.
【详解】（1）
连接，，
因为点，，分别为，，的中点，
所以且，，，
所以，且，
所以四边形是平行四边形，所以，
又因为平面，平面，
所以平面
（2）
因为平面，平面，所以，，
又因为，，平面，所以平面，
所以即是直线与平面所成的角，
所以，
因为，所以，
因为，，所以，
因为，平面，所以平面，
所以，
因为，
所以，，所以，
由（1）知多面体为四棱锥，且四边形是平行四边形，
所以.
23．（1）或或或；（2）证明见解析；（3）.
【分析】（1）根据“鳖臑”的概念，由题意，由线面垂直的判定定理和性质，直接补充条件即可；
（2）（i）根据线面垂直的判定定理，先证明平面，平面，推出，；再得到平面，根据面面垂直的判定定理，即可证明面面垂直；
（ii）先由题意，设，连结，则即为，根据线面垂直的判定定理和性质，证明即为二面角的一个平面角，再由题中数据，直接计算，即可得出结果.
【详解】（1）因为“鳖臑”是由四个直角三角形组成的四面体，又平面，所以，，；即，为直角三角形；
若，由，平面，可得：平面；
所以，即，为直角三角形；满足四个面都是直角三角形；
同理，可得或或，都能满足四个面都是直角三角形；
故可填：或或或；
（2）（i）证明：
∵平面，平面，
∴，
又，，平面，
∴平面，
又平面，
∴，
又，，平面，
∴平面，
又平面，
∴，
又，，平面，
∴平面，
又平面，
∴平面平面.
（ii）由题意知，在平面中，直线与直线相交.
如图所示，设，连结，则即为.
∵平面，平面，
∴，
∵平面，平面，
∴，
又，平面，
∴平面，
又平面，
∴，.
∴即为二面角的一个平面角.
在中，，，，
∴，
又，
∴，
∴，
∴，
∴二面角的大小为.

【点睛】本题主要考查证明面面垂直，考查求二面角的大小，熟记线面垂直与面面垂直的判定定理，以及二面角的求法即可，属于常考题型.
24．(1)证明见解析；
(2).
【分析】（1）作于点连接，可证，，可证直线平面，即可证明；
（2）以点为原点，,,所在直线为轴，建立如图所示空间直角坐标系，利用空间向量可求二面角的余弦值.
【详解】（1）证明：作于点连接，
∵，，，
∴，∴，
即，，又，
∴平面，又平面，
∴.
（2）∵二面角的大小为，
∴平面平面，平面平面，，∴平面.
以点为原点，,,所在直线为轴，建立如图所示空间直角坐标系，
∵,
∴.
∴，即.
∴，，，.
∴,，
设平面的法向量，
由，得
令，得.
易知为平面的一个法向量.
设二面角为，为锐角，则.
25．（1）见解析（2）
【分析】（1）过D作，垂直为O，连接，利用勾股定理证得，结合，证得平面，即可得到平面平面；
（2）建立空间直角坐标系，求出两平面的法向量，通过计算法向量的夹角的余弦值，求得的长，再结合线面角的定义，即可求解.
【详解】（1）过D作，垂直为O，连接，
在中，，，可得，
在中，
由余弦定理可得，
所以，
因为，所以为等边三角形，所以，
所以，可得，又由，且，
所以平面，又平面，所以平面平面.
（2）由（1）知，以O为原点，，，方向分别为x，y，z轴正方向，建立空间直角坐标系
设，则，，，，
所以，
设平面的法向量为，则，即
令，，
平面的法向量为，
由，解得
因为平面，所以为与平面所成的角，所以，
即直线与平面所成角正弦值.
【点睛】本题考查了面面垂直的判定，以及空间角的求解问题，意在考查学生的空间想象能力和逻辑推理能力，解答中熟记线面位置关系的判定定理和性质定理，通过严密推理是线面位置关系判定的关键，同时对于立体几何中角的计算问题，往往可以利用空间向量法，通过求解平面的法向量，利用向量的夹角公式求解.
26．(1)见解析；
(2).
【分析】（1）利用和全等，得出，通过构建线面垂直达到证明的目的；
（2）利用面面垂直的性质定理可得出线面垂直，再根据几何方法作出二面角的平面角进行求解.
【详解】（1）∵，，.∴，
∴，取的中点，连接，，则，.
又∵，平面，平面，∴平面，又平面，∴.
（2）过作于点，则平面，
又∵平面平面，平面平面，
∴平面. 过作于点，连接.
∵平面，平面，∴
又，平面，∴平面，平面
∴，根据二面角的定义，∴为二面角的平面角.
连接，∵，由于，∴.
∵，，∴，.
∵，，∴，根据等面积法：.
∴，显然是锐角，根据同角三角函数的关系
易得：，故二面角的余弦值为.
27．(1)证明见解析
(2).
【分析】
（1）利用余弦定理与勾股定理推得，再利用线面垂直与面面垂直的判定定理与性质定理即可得证；
（2）建立空间直角坐标系，利用线面角的向量表示得到关于的表达式，从而求得的值，进而利用点面距离公式即可得解.
【详解】（1）
如图，设交于点，连接，由圆锥的性质可知底面，

因为平面，所以，
又因为是底面圆的内接正三角形，由，可得，，
解得，又，，
所以，即，，
所以在中，，
在中，由余弦定理：
，
所以，故.
因为底面，面，所以平面平面，
又面，面面，，故面，
又平面，所以平面平面；
（2）
易知，以点为坐标原点，，，所在直线分别为x轴，y轴，z轴，建立如图所示的空间直角坐标系，

则，，，，，，
所以，，，，
设平面的法向量为，则，
令，则，
设，可得，
设直线与平面所成的角为，则，
即，
令，，
则
当且仅当，即时，等号成立，
所以当时，有最大值4，
即当时，的最大值为1，此时点，
所以，
所以点M到平面的距离，
故当直线与平面所成角的正弦值最大时，点到平面的距离为.
28．(1)
(2).
【分析】（1）利用同底等高的锥体与柱体的体积关系，利用割补法即可求解.
（2）利用垂直关系证明出线面垂直，建立空间直角坐标系，求出两个平面的法向量，假设平面夹角为，利用夹角公式求解即可.
【详解】（1）因为四棱锥的体积为2，所以三棱锥的体积为
因为是边长为2的正三角形，所以的面积.
设三棱柱的高为，
则，
解得.
（2）作，垂足为，连接.
因为平面平面，且平面平面，所以平面，
即为三棱柱的高，由（1）可知.
因为，所以，所以.
因为为锐角，所以为的中点，则.
因为平面平面，且平面平面，
所以平面，
所以三线两两垂直，故以为坐标原点，分别以，
的方向为轴的正方向建立空间直角坐标系.
由题中数据可得，
，则.
设平面的法向量为，
则令，得.
设平面的法向量为，
则令，得.
设平面与平面的夹角为，
则.
故平面与平面的夹角的余弦值为.
29．(1)证明见解析
(2)
(3)
【分析】（1）由题意建立空间直角坐标系，求出平面的法向量，根据即可证明平面；
（2）由点到平面距离的向量表示公式，代入数据即可求解；
（3）由直线与底面所成角的正弦值为可求出，然后根据两平面的法向量求所成角的余弦值即可.
【详解】（1）连接，因为，，
所以四边形为平行四边形，所以，
以为坐标原点，建立如图所示的空间直角坐标系：
则，，，，,
因为是的中点，所以，
，，，
设平面的一个法向量为，
则，即，
取，则，
又因为平面，所以平面.
（2）由（1）知，，，所以，
且平面的一个法向量为，
所以点到平面的距离.
（3）由题意知，底面的法向量为，
因为，，
且，，所以，
所以由题意知：，
解得：，所以，
因为，设平面的一个法向量为，
则，即，取，
所以，
又平面与平面夹角为锐角，
所以平面与平面夹角的余弦值为.
30．（1）证明见解析；（2）点靠近点的六等分点处.
【分析】（1）连接，证明//即可得到结果；
（2）先证明平面，证明，则可以点为原点，分别以,，为，，轴建立空间直角坐标系，计算出平面的法向量为，假设，表示出，利用与法向量的夹角的余弦值的绝对值为求解出，则可确定点的位置.
【详解】（1）因为斜三棱柱斜三棱柱各侧面均为平行四边形
则是的中点
又分别是棱，的中点，
则
又则四边形为平行四边形
则为的中点
则在三角形中，//
连接则//
所以//
又平面平面；
则//平面；
（2）点在底面投影为边的中点，
所以平面,
又因为三角形为正三角形，为中点，
所以
分别以所在直线为分别为轴，建立空间直角坐标系，
如图所示：
因为，，，则，，
所以，，，，，，，，，
设
则
所以
设平面的一个法向量
则，
，
令，，
所以.
设AM与平面所成角为
所以
令
同联立可得
当时，即点靠近点的六等分点处时，符号条件.
【点睛】本题考查线面平行的证明，考查已知线面夹角的正弦值确定动点位置的问题，难度较大.线面夹角问题可采用空间向量法计算，将问题转化为求直线的方向向量与平面的法向量夹角来解答.
31．(1)证明见解析；(2)
【分析】(1) 取中点，证明⊥平面，即可证明.
(2)建立空间直角坐标系，找出直线与平面所成角，根据直线与平面所成角的正弦值，求得直线与平面所成角.
【详解】（1）证明：取的中点，连接，，
因为,则，
又因为,则，
，
⊥平面，
平面，
.
（2）由(1)知，，
二面角的平面角，
以为坐标原点建立如图所示的空间直角坐标系，
，，，，
，，
，，
设平面的法向量为：，
，得，
令，则，
又，
设直线与平面所成角为，
则，
即，化简得，
解得或，
由题意可知，
所以.
【点睛】本题主要考查的是空间几何体的应用，线面垂直，线面角，二面角的应用，是难题.
32．(1)证明见解析
(2)
【分析】（1）由已知，由可得，由平面，可利用线面垂直的性质定理推出，然后利用线面垂直的判定定理推出平面，然后再利用面面垂直的判定定理推出平面平面；
（2）取，的中点，以为坐标原点，建立空间直角坐标系，分别为轴的正方向，设，根据三棱台的体积为，计算出，从而表示出各点坐标，设出平面和平面的法向量，先求解，然后再利用同角三角函数关系求解正弦值.
【详解】（1）
由已知，平面，平面，所以，
在三棱台中，，所以，所以，
又因为平面，且，
所以平面，又因为平面，
所以平面平面，得证.
（2）
取，的中点，连接，所以，
又因为，所以，
因为平面，平面，所以，
又因为，为的中点，所以，
由（1）问可知，平面平面，且平面平面，
所以平面，
以为坐标原点，建立空间直角坐标系，分别为轴的正方向，
因为，，且，所以，
所以，，，，，，
在三棱台中，设，
，， ，
所以或，所以，
所以，
设平面的法向量为，
，，
由可知，平面的一条法向量为，
设平面的法向量为，
，，
由可知，平面的一条法向量为，
所以，
所以二面角的正弦值为.
33．(1)证明见解析
(2)证明见解析
(3)
【分析】
（1）由已知得出，即可根据线面平行的判定证明；
（2）取的中点，连接，过作平面，垂足为，连接，，，，通过已知得，通过线面垂直的判定与性质得出，通过中位线得出，即可得出，再通过勾股定理得出，即可证明；
（3）以为坐标原点，的方向为轴的正方向建立空间直角坐标系，得出各点坐标，通过点到平面距离的向量求法即可求出.
【详解】（1）因为，
所以，，
所以，
因为平面，平面，
所以平面.
（2）取的中点，连接，则四边形为正方形.
过作平面，垂足为.
连接，，，.

由和均为正三角形，得，
所以，即点为正方形对角线的交点，
则.
因为平面，且平面，
所以，
又，且平面,平面,
所以平面，
因为平面，
所以.
因为是的中点，是的中点，
所以，
因此.
因为，
所以，
又，平面，平面，
所以平面.
（3）设，连接，则直线为直线，
因为，平面，平面，
所以平面，
因为平面，且平面平面，
所以.
由（1）知，，，两两垂直，以为坐标原点，的方向为轴的正方向建立如图所示的空间直角坐标系，

则，，，，，
，，
设平面的法向量为，则，
所以，
取，得.
又，
所以点到平面的距离.
34．(1)证明见解析
(2)，平行六面体的体积为，的值表示以，，为邻边的平行六面体的体积
【分析】（1）利用向量法证明，，从而可得平面，即可得证；
（2）根据公式求出，利用棱柱的体积公式求出该棱住的体积，从而可得出结论.
【详解】（1）证明：由题意，，
∴，，即，，
∵，是平面内两相交直线，∴平面，
∴平行六面体是直四棱柱；
（2）解：，
由题意，，，
，所以，
，，
∴.
∴，
故的值表示以，，为邻边的平行六面体的体积.
35．（1）证明见解析；（2）.
【分析】（1）、因为为平面的法向量，所以即，代入坐标化简即可证明；
（2）、设平面的法向量为，则，推导出平面的法向量代入（1）中的结论即可得到平面的点法式方程.
【详解】（1）平面经过点，点是平面内任意一点.
,
为平面的法向量
（2）设平面的法向量为，
，
则，令则，平面的法向量为
由（1）可知，平面的点法式方程为：即
36．（1）；（2）证明见解析.
【分析】（1）四棱锥的总曲率等于四棱锥各顶点的曲率之和，写出多边形表面的所有内角即可.（2）设顶点数、棱数、面数分别为、、，设第个面的棱数为，所以，按照公式计算总曲率即可.
【详解】（1）由题可知：四棱锥的总曲率等于四棱锥各顶点的曲率之和.

可以从整个多面体的角度考虑，所有顶点相关的面角就是多面体的所有多边形表面的内角的集合.由图可知：四棱锥共有5个顶点，5个面，其中4个为三角形，1个为四边形.
所以四棱锥的表面内角和由4个为三角形，1个为四边形组成，
则其总曲率为：.
（2）设顶点数、棱数、面数分别为、、，所以有
设第个面的棱数为，所以
所以总曲率为：
所以这类多面体的总曲率是常数.
【点睛】本题考查立体几何的新定义问题，能够正确读懂“曲率”的概率是解决问题的关键．