2025年高考数学一轮复习-3.3-导数与函数的极值、最值【课件】

这是一份2025年高考数学一轮复习-3.3-导数与函数的极值、最值【课件】，共60页。

1.借助函数的图象，了解函数在某点取得极值的必要条件和充分条件.
2.能利用导数求某些函数的极大值、极小值以及给定闭区间上不超过三次的多项式函数的最大值、最小值.
3.体会导数与单调性、极值、最大（小）值的关系.
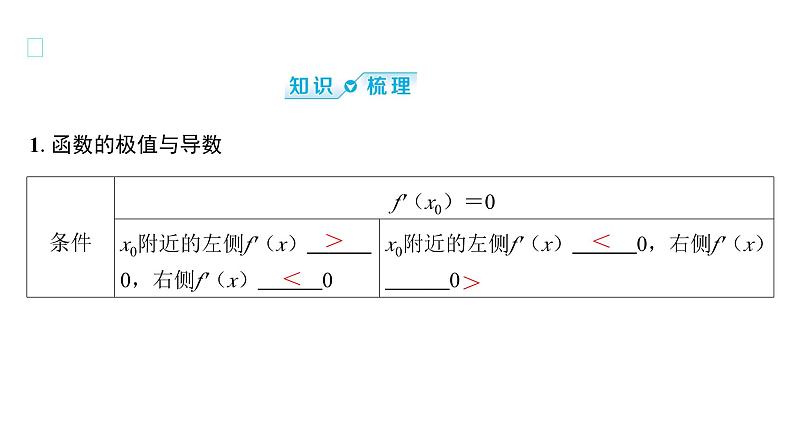
　　　　　　　　知识·逐点夯实
提醒　f'（x0）＝0是x0为可导函数f（x）的极值点的必要不充分条件.如：f（x）＝x3，f'（0）＝0，但x＝0不是极值点.
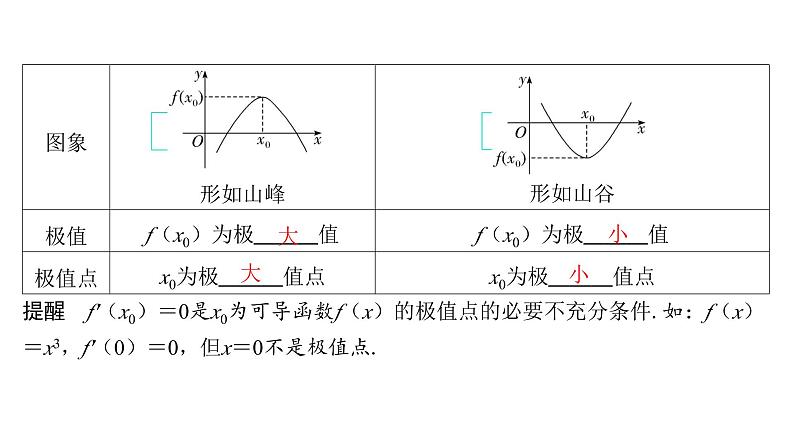
2.函数的最值与导数（1）如果在区间[a，b]上函数y＝f（x）的图象是一条 　连续不断　⁠的曲线，那么它必有最大值和最小值；（2）若函数f（x）在[a，b]上单调递增，则f（a）为函数的 　最小值　⁠，f（b）为函数的 　最大值　⁠；若函数f（x）在[a，b]上单调递减，则f（a）为函数的 　最大值　⁠，f（b）为函数的 　最小值　⁠.
1.判断正误.（正确的画“√”，错误的画“×”）
（1）函数的极大值不一定比极小值大.（　　）
（2）闭区间上的连续函数必有最值.（　　）
（3）函数的极大值一定是函数的最大值.（　　）
（4）开区间上的单调连续函数无最值.（　　）
（5）设函数y＝f（x）在区间（a，b）内有极值，那么y＝f（x）在区间（a，b）内不单调.（　　）
2.（多选）已知函数y＝f（x）的导函数f'（x）的图象如图所示，则下列判断正确的是（　　）
4.函数 g（x）＝－x2的极值点是 　　　　⁠，函数f（x）＝（x－1）3的极值点 　　　　⁠（填“存在”或“不存在”）. 
解析：结合函数图象可知g（x）＝－x2的极值点是x＝0.因为f'（x）＝3（x－1）2≥0，所以f'（x）＝0无变号零点，故函数f（x）＝（x－1）3不存在极值点.
5.（2023·安阳一模）函数f（x）＝x3－3x2＋1的极小值为 　　　　⁠. 
解析：f'（x）＝3x2－6x，令f'（x）＝3x2－6x＝0，得x1＝0，x2＝2.易知当x∈（－∞，0）时，f'（x）＞0；当x∈（0，2）时，f'（x）＜0；当x∈（2，＋∞）时，f'（x）＞0.故f（x）在x＝2处取得极小值f（2）＝8－12＋1＝－3.
1.若函数f（x）在（a，b）上是单调函数，则f（x）在（a，b）上无极值.
2.若函数f（x）在[a，b]上是单调函数，则f（x）一定在区间端点处取得最值.
3.若函数f（x）在区间（a，b）内只有一个极值点，则该极值点一定是函数相应的最值点.
考向1　由图象判断函数的极值
【例1】　设函数f（x）在R上可导，其导函数为f'（x），且函数y＝（x－1）f'（x）的图象如图所示，则下列结论中正确的是（　　）
解析　结合题目所给图象进行分段分析，当x＜－3时，x－1＜0，得f'（x）＜0；当－3＜x＜1时，x－1＜0，得f'（x）＞0；当1＜x＜3时，x－1＞0，得f'（x）＞0；当x＞3时，x－1＞0，得f'（x）＜0.根据极值点的定义可知，当x＝－3时，f（x）取得极小值f（－3），当x＝3时，f（x）取得极大值f（3），x＝1的左右两边导函数值都大于零，因此不是原函数的极值点，故选D.
｜解题技法｜　　由图象判断函数y＝f（x）的极值，要抓住两点：（1）由y＝f'（x）的图象与x轴的交点，可得函数y＝f（x）的可能极值点；（2）由导函数y＝f'（x）的图象可以看出y＝f'（x）的值的正负，从而可得函数y＝f（x）的单调性.两者结合可得极值点.
考向2　求函数的极值（极值点）【例2】　已知函数f（x）＝ln x－ax（a∈R）.
故f（x）在定义域上的极大值为f（2）＝ln 2－1，无极小值.
（2）讨论函数f（x）在定义域内极值点的个数.
利用导数求函数极值（极值点）的一般流程
考向3　已知函数的极值求参数
【例3】　（1）（2023·南宁模拟）函数f（x）＝x3＋ax2＋bx＋a2在x＝1处取得极值10，则a＋b＝（　　）
（2）已知函数f（x）＝x2－4x＋aln x有两个极值点，则实数a的取值范围为（　　）
｜解题技法｜已知函数极值点或极值求参数的2个要领（1）列式：根据极值点处导数为0和极值这两个条件列方程组，利用待定系数法求解；（2）验证：因为导数值等于零不是此点为极值点的充要条件，所以利用待定系数法求解后必须验证根的合理性.提醒　若函数y＝f（x）在区间（a，b）内有极值，那么y＝f（x）在（a，b）内绝不是单调函数.
1.（2024·周口一模）函数f（x）＝2x－xln x的极值是（　　）
解析：C　因为f'（x）＝2－（ln x＋1）＝1－ln x，当f'（x）＞0时，解得0＜x＜e；当f'（x）＜0时，解得x＞e，所以x＝e时，f（x）取到极大值，f（x）极大值＝f（e）＝e.故选C.
｜解题技法｜利用导数求给定区间上的最值的步骤（1）求函数f（x）的导数f'（x）；（2）利用f'（x）＝0求f（x）在给定区间上所有可能极值点的函数值；（3）求f（x）在给定区间上的端点值；（4）将f（x）的各极值与f（x）的端点值进行比较，确定f（x）的最大值与最小值.提醒　若最值在端点处取得，且所给区间为开区间，则f（x）的最值不存在.
1.已知某圆柱的表面积为6π，当该圆柱的体积最大时，其底面半径为（　　）
2.已知函数f（x）＝ax＋ln x，其中a为常数，若f（x）在区间（0，e]上的最大值为－3，求a的值.
1.函数f（x）＝ln x－x在区间（0，e]上的最大值为（　　）
5.（多选）已知函数f（x）的定义域为[－1，5]，部分对应值如下表：
f（x）的导函数f'（x）的图象如图所示，下列关于函数f（x）的结论正确的是（　　）
解析：AB　由题中f'（x）的图象可知，当x＝0时，函数f（x）取得极大值；当x＝4时，函数f（x）取得极大值，即函数f（x）有2个极大值点，故A中结论正确；易知函数f（x）在[0，2]上是减函数，故B中结论正确；当x∈[－1，t]时，若f（x）的最大值是2，则t满足0≤t≤5，即t的最大值是5，故C中结论错误；令y＝f（x）－a＝0，得f（x）＝a，当f（2）≤1，1＜a＜2时，易知f（x）＝a有四个根；当1＜f（2）＜2，1＜a＜2时，易知f（x）＝a不一定有四个根，故函数y＝f（x）－a有4个零点不一定正确，故D中结论错误，故选A、B.
6.（多选）下列说法正确的是（　　）
10.已知a，b是实数，1和－1是函数f（x）＝x3＋ax2＋bx的两个极值点.
解：（1）由题设知f'（x）＝3x2＋2ax＋b，且f'（－1）＝3－2a＋b＝0，f'（1）＝3＋2a＋b＝0，解得a＝0，b＝－3.
（2）设函数g（x）的导函数g'（x）＝f（x）＋2，求g（x）的极值点.
解：（2）由（1）知f（x）＝x3－3x，则g'（x）＝f（x）＋2＝（x－1）2（x＋2），所以g'（x）＝0的根为x1＝x2＝1，x3＝－2.即函数g（x）的极值点只可能是1或－2，当x＜－2时，g'（x）＜0，当－2＜x＜1时，g'（x）＞0，当x＞1时，g'（x）＞0，所以－2是g（x）的极值点，1不是g（x）的极值点.综上所述，g（x）的极值点为－2.
11.某商场从生产厂家以每件20元的价格购进一批商品，若该商品零售价定为p（p≥20）元时的销售量为Q件，且Q＝8 300－170p－p2，则这批商品的最大毛利润（毛利润＝销售收入－进货支出）为（　　）
解析：D　设毛利润为L（p）元，由题意知L（p）＝pQ－20Q＝Q（p－20）＝（8 300－170p－p2）（p－20）＝－p3－150p2＋11 700p－166 000（p≥20），所以L'（p）＝－3p2－300p＋11 700.令L'（p）＝0，解得p＝30或p＝－130（舍去）.因为当20≤p＜30时，L'（p）＞0，当p＞30时，L'（p）＜0，所以L（30）是极大值，根据实际问题的意义知，L（30）也是最大值，此时，L（30）＝23 000，即零售价定为每件30元时，最大毛利润为23 000元.故选D.
13.（2024·新高考Ⅰ卷）函数f（x）＝｜2x－1｜－2ln x的最小值为 　　　　⁠. 
（1）求函数f（x）的单调区间；
15.如果存在函数g（x）＝ax＋b（a，b为常数），使得对函数f（x）定义域内任意的x都有f（x）≤g（x）成立，那么g（x）为函数f（x）的一个“线性覆盖函数”.已知f（x）＝－2xln x－x2，g（x）＝－ax＋3，若g（x）为函数f（x）在区间（0，＋∞）上的一个“线性覆盖函数”，则实数a的取值范围是（　　）
（1）求证：函数y＝f（x）的拐点M（x0，f（x0））在直线y＝ax上；
（2）x∈（0，2π）时，讨论f（x）的极值点的个数.