河北省沧州市东光县三校联考2023-2024学年七年级下学期期中数学试卷(含答案)

这是一份河北省沧州市东光县三校联考2023-2024学年七年级下学期期中数学试卷(含答案)，共16页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。

一、单选题
1．在下列各数中,最小的数是( )
A.B.0C.1D.
2．在实数,0,,1.8中,最小的是( )
A.B.0C.D.1.8
3．若,,则的值等于( )
A.9B.2C.D.不能求出
4．已知代数式与是同类项,那么m、n的值分别是( )
A.,B.,
C.,D.,
5．下列等式正确的是( )
A.B.C.D.
6．根据等式的性质,下列变形错误的是( )
A.若,则B.若,则
C.若,则D.若,则
7．利用加减消元法解方程,下列做法正确的是( )
A.要消去x,可以将
B.要消去x,可以将
C.要消去y,可以将
D.要消去y,可以将
8．若,则( )
A.4B.5C.D.
9．已知不等式组的解都是关于x的一次不等式的解,则a的取值范围是( )
A.B.C.D.或
10．在平面直角坐标系中,已知点,,其中a为整数.点C在线段上,且点C的横、纵坐标均为整数.若点C在y轴上,则满足条件的点C的坐标有( )个.
A.3B.4C.6D.7
11．下列图形中和是对顶角的是( )
A.B.
C.D.
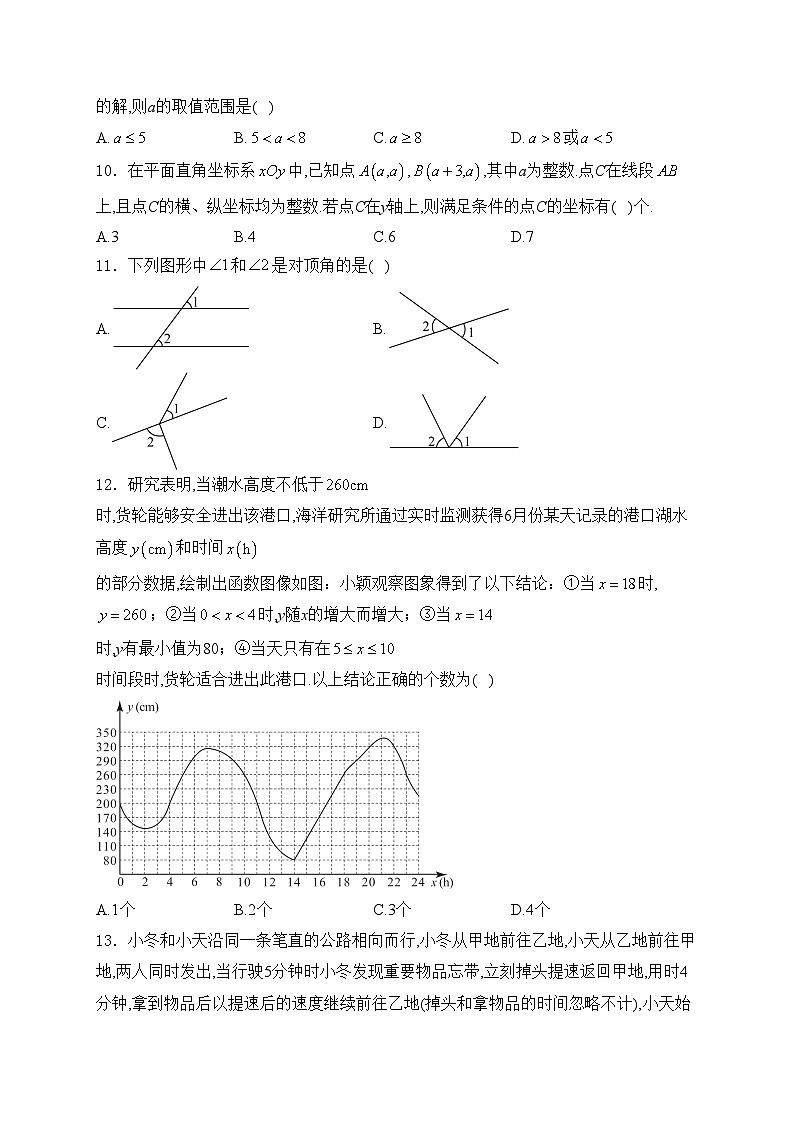
12．研究表明,当潮水高度不低于时,货轮能够安全进出该港口,海洋研究所通过实时监测获得6月份某天记录的港口湖水高度和时间的部分数据,绘制出函数图像如图：小颖观察图象得到了以下结论：①当时,；②当时,y随x的增大而增大；③当时,y有最小值为80；④当天只有在时间段时,货轮适合进出此港口.以上结论正确的个数为( )
A.1个B.2个C.3个D.4个
13．小冬和小天沿同一条笔直的公路相向而行,小冬从甲地前往乙地,小天从乙地前往甲地,两人同时发出,当行驶5分钟时小冬发现重要物品忘带,立刻掉头提速返回甲地,用时4分钟,拿到物品后以提速后的速度继续前往乙地(掉头和拿物品的时间忽略不计),小天始终以一个速度保持行驶,二人相距的路程y(米)与小冬出发时间x(分钟)之间的关系如图所示,则下列说法中错误的是( )
A.小冬返回甲地的速度与小天行驶速度相同；
B.小冬和小天出发时的速度分别为160米/分钟和200米/分钟；
C.小天出发14.5分钟两人相遇；
D.小冬最终达到乙地的时间是20分钟.
14．如图,从边长为的大正方形纸片中剪去一个边长为的小正方形,剩余部分沿虚线剪开,拼成一个矩形(不重叠无缝隙),则矩形的面积为( )
A.B.
C.D.
15．如图,已知,点E在直线上,点F,G在直线上,于点E,,则的度数是( )
A.B.C.D.
16．如图,已知点P是射线上一动点(不与点O重合),,若是钝角三角形,则的取值范围是( )
A.B.
C.或D.或
二、填空题
17．已知二元一次方程,若用含x的代数式表示y,可得_____.
18．若关于x的方程的解是,则a的值为__________.
19．如图,的中线、相交于点F,的面积为6,则四边形的面积为______.
20．如图,甲所示三角形纸片中,,将纸片沿过点B的直线折叠,使点C落到边上的E点处,折痕为(如图乙).再将纸片沿过点E的直线折叠,点A恰好与点D重合,折痕为(如图丙),则的大小为________.
三、解答题
21．计算
(1)；
(2).
(3)；
(4).
22．先化简再求值：,其中.
23．已知的结果中不含x的一次项.
(1)求a的值；
(2)化简：,并在(1)的条件下求值.
24．如图,D是上一点,E是上一点,,,,,求的度数.
25．如图,四边形中,点E和点F和分别为边和上的点,并且,.
(1)请判断直线和直线的位置关系,并证明你的结论；
(2)若是的角平分线,,,求的度数.
26．某学校准备组织290名学生进行野外考察活动,共有100件行李,学校计划租用甲、乙两种型号的汽车共8辆,经了解,甲种汽车每辆最多能载40人和10件行李,乙种汽车每辆最多能载30人和20件行李,
(1)设租用甲种汽车x辆,请你帮助学校设计所有可能的租车方案；
(2)如果甲、乙两种汽车每辆的租车费用分别为2000元、1800元,请你选择最省钱的一种租车方案.
27．【动手操作】
小明将一副三角板中的两个直角顶点C按如图1方式叠放在一起,其中,,.三角板固定不动,将三角板绕点C顺时针旋转.
【发现问题】
小明发现,在旋转三角板的过程中,有些角之间的存在着特殊的数量关系；某两条边在某个瞬间,有特殊的位置关系.
【解决问题】
(1)当三角板旋转至如图2所示的位置时.
求证：
求证：
(2)小明将三角板从图1所示的位置开始绕点C以每秒的速度按顺时针方向旋转,设旋转时间为t秒,当旋转到延长线上时,小明停止旋转.
如图3.当时,求t的值；
当三角板中的边与三角板中的某条边平行时,求t的值.
参考答案
1．答案：D
解析：,
故选D.
2．答案：A
解析：根据题意,得,
故选A.
3．答案：A
解析：由得,
由得,
设,,
则,
解得：,
,
故选A.
4．答案：B
解析：依题意得：,
解得：,
故选B.
5．答案：D
解析：A、,故A错误.
B、,故B错误.
C、,故C错误.
D、,故D正确.
故选：D.
6．答案：B
解析：若,则,故A选项变形正确,不符合题意；
若且,则,故B选项变形错误,符合题意；
若,则,故C选项变形正确,不符合题意；
若,则,故D选项变形正确,不符合题意；
故选B.
7．答案：A
解析：利用加减消元法解方程,要消去x,可以将,
要消去y,可以将,
故选A.
8．答案：A
解析：令,则原等式变形为：,
整理得,
解得,
,
,即,
故选A.
9．答案：C
解析：由,得：,
由,得：,
则不等式组的解集为,
由,解得,
不等式组的解都是关于x的一次不等式的解,
,
故选C.
10．答案：B
解析：当时,如图1,
此时,线段上不存在点C在y轴上；
当时,如图2,
此时,线段上不存在点C在y轴上；
∵a为整数,
∴a的取值为,,,0,
∴满足条件的点C的坐标有4个；
当,如图3,
此时,线段上不存在点C在y轴上；
综上,满足条件的点C的坐标有4个,
故选：B.
11．答案：B
解析：根据定义,B选项中,和有一个公共顶点,并且一个角的两边分别是另一个角的两边的反向延长线,即和是对顶角,其他图形不满足对顶角的定义,
故选：B.
12．答案：B
解析：由图象可得：当时,；故①符合题意；
当时,y随x先减小后增大；故②不符合题意；
当时,y有最小值为80；故③符合题意；
当天在或时间段时,货轮适合进出此港口.故④不符合题意；
故选B
13．答案：D
解析：A.当行驶5分钟时小冬发现重要物品忘带发现重要物品没带,立刻掉头提速返回甲地甲地,此时由图轴可知,小东和小天相距的路程不变,
所以小冬返回甲地的速度与小天行驶速度相同,
此选项不符合题意
B.小东掉头提速返回甲地,用时4分钟,且小东和小天相距的路程不变
小东提速前5分钟的路程,相当于小天只需4分钟就可走完,
小天速度是小东提速前的速度的倍
设小东原速度为v米/分钟,则提速后为米/分钟,小天的速度为米/分钟,则
小冬和小天出发时的速度分别为160米/分钟和200米/分钟,
故此选项不符合题意；
C.两人同时发出,当行驶5分钟到达B点,小东掉头提速返回甲地,用时4分钟,且小东和小天相距的路程不变,
此时两人相距2200米,
拿到物品后以提速后的速度继续前往乙地,
小东提速后速度为200米/分钟,两人继续行驶分钟相遇,
小天一共行驶了分钟
故此选项不符合题意；
D.小东行驶时间为开始5分钟,返回甲地4分钟,重新返回乙地分钟,
小冬最终达到乙地的时间是29分钟,
故此选项不符合题意.
故选：D.
14．答案：B
解析：长方形的面积为：
,
故选B.
15．答案：C
解析：∵,
∴,
∵,
∴,
∵,
∴,
故选：C.
16．答案：D
解析：由题意知,分是钝角,是钝角两种情况求解；
当是钝角时,；
当是钝角时,,即,
∴；
综上所述,或,
故选：D.
17．答案：
解析：∵,
∴,
∴.
故答案为：.
18．答案：3
解析：根据题意,知
,
解得.
故答案是：3.
19．答案：
解析：∵的中线、相交于点F,
∴,
∴,
∴,
故答案为：6.
20．答案：120
解析：由折叠得,,
又,
,
,
,
,
,
故答案为：120.
21．答案：(1)2
(2)
(3)1
(4)
解析：(1)
；
(2)
；
(3)
；
(4)
.
22．答案：,2023
解析：
,
当时,
原式.
23．答案：(1)
(2),17
解析：(1),
∵不含x的一次项
,
∴；
(2)
=
=；
∴当时,原式.
24．答案：60度
解析：∵,,
∴
∴,
∴,
∵,
∴.
25．答案：(1),理由见解析
(2)
解析：(1),理由如下：
∵,,,
∴,
∵,
∴,
∴；
(2)∵,
∴,
∵,
∵,,
∴,
由(1)知,,
∴,
∵是的角平分线,
∴.
26．答案：(1)共有2种租车方案：第一种是租用甲种汽车5辆,乙种汽车3辆；第二种是租用甲种汽车6辆,乙种汽车2辆
(2)第一种租车方案更省费用
解析：(1)租用甲种汽车x辆,则租用乙种汽车辆.
根据题意,得解得.
因为x为整数,所以或6.
所以有两种租车方案,方案一：租用甲种汽车5辆,乙种汽车3辆；方案二：租用甲种汽车6辆,乙种汽车2辆.
(2)方案一的费用：(元)；
方案二的费用：(元).
因为15600元元,所以方案一更省钱.
所以第一种租车方案最省钱,即学校应租用甲种汽车5辆,乙种汽车3辆.
27．答案：(1)①证明见解析
②证明见解析
(2)①40
②15或45或55
解析：(1)证明：①∵,,
∴；
②∵,,
∴,
∵,
∴；
(2)①∵,
∴,
∴,
∴；
②当时,则,
∴
当时,则,
∴,
∴；
当时,延长交于F,则,
∴,
∴；
综上所述,t的值为15或45或55.