

人教版七年级数学下册精选压轴题汇编培优卷专题04规律型:点的坐标(原卷版+解析)
展开姓名:___________班级:___________考号:___________
一.选择题(共10小题,满分20分,每小题2分)
1.(2分)(2022春•江夏区校级月考)如图,长方形BCDE的各边分别平行于x轴或y轴,物体甲和物体乙分别由点A(4,0),F(﹣4,0)同时出发,沿长方形BCDE的边作环绕运动.物体甲按逆时针方向以4个单位/秒匀速运动,物体乙按顺时针方向以2个单位/秒匀速运动,则两个物体运动后的第2022次相遇地点的坐标是( )
A.(2,﹣2)B.(﹣2,﹣2)C.(﹣2,2)D.(2,2)
2.(2分)(2022春•惠州期末)如图所示,在平面直角坐标系中,有若干个点按如下规律排列:(1,1),(2,1),(2,2),(3,1),(3,2),(3,3)……,则第50个点的坐标为( )
A.(7,6)B.(8,8)C.(9,6)D.(10,5)
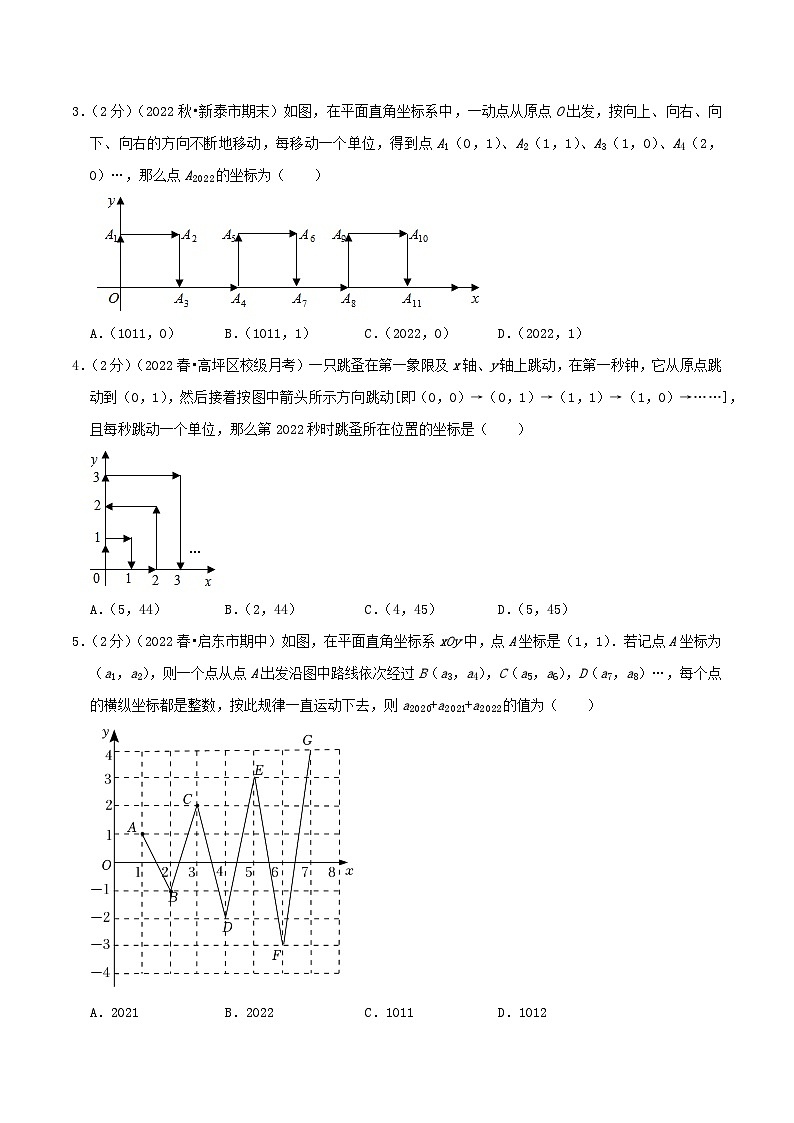
3.(2分)(2022秋•新泰市期末)如图,在平面直角坐标系中,一动点从原点O出发,按向上、向右、向下、向右的方向不断地移动,每移动一个单位,得到点A1(0,1)、A2(1,1)、A3(1,0)、A4(2,0)…,那么点A2022的坐标为( )
A.(1011,0)B.(1011,1)C.(2022,0)D.(2022,1)
4.(2分)(2022春•高坪区校级月考)一只跳蚤在第一象限及x轴、y轴上跳动,在第一秒钟,它从原点跳动到(0,1),然后接着按图中箭头所示方向跳动[即(0,0)→(0,1)→(1,1)→(1,0)→……],且每秒跳动一个单位,那么第2022秒时跳蚤所在位置的坐标是( )
A.(5,44)B.(2,44)C.(4,45)D.(5,45)
5.(2分)(2022春•启东市期中)如图,在平面直角坐标系xOy中,点A坐标是(1,1).若记点A坐标为(a1,a2),则一个点从点A出发沿图中路线依次经过B(a3,a4),C(a5,a6),D(a7,a8)…,每个点的横纵坐标都是整数,按此规律一直运动下去,则a2020+a2021+a2022的值为( )
A.2021B.2022C.1011D.1012
6.(2分)(2022春•东莞市校级期中)如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2),…,按这样的运动规律,经过第30次运动后,动点P的坐标是( )
A.(30,1)B.(30,0)C.(30,2)D.(31,0)
7.(2分)(2022春•武昌区期中)如图,动点P从(0,3)出发,沿所示方向运动,每当碰到矩形的边时反弹,反弹时反射角等于入射角(∠AOM=∠BOM),当点P第2022次碰到矩形的边时,点P的坐标为( )
A.(0,3)B.(5,0)C.(1,4)D.(8,3)
8.(2分)(2022春•突泉县期末)如图,正方形的边长依次为2,4,6,8,……,他们在直角坐标系中的位置如图所示,其中A1(1,1),A2(﹣1,1),A3(﹣1.﹣1),A1(1,﹣1),A5(2.,2),A6(﹣2,2),A7(﹣2,﹣2),A8(2.﹣2),A9(3,3),A10(﹣3,3),……,按此规律接下去,则A2016的坐标为( )
A.(﹣504,﹣504)B.(504,﹣504)
C.(﹣504,504)D.(504,504)
9.(2分)(2022春•满城区校级期末)如图,在单位面积为1的方格纸上,A1,A2,A3,A4,A5,…均在格点上,且坐标分别为A1(2,0),A2(1,﹣1),A3(0,0),A4(2,2),A5(4,0),…,则依图中所示规律,点A2022的纵坐标为( )
A.﹣1010B.1010C.﹣1011D.1011
10.(2分)(2022春•合江县期末)在平面直角坐标系中,一个智能机器人接到如下指令:从原点O出发,按向右,向上,向右,向下的方向依次不断移动,每次移动1m,其行走路线如图所示,第一次移动到A1,第二次移动到A2,…,第n次移动到An,则A2022的坐标是( )
A.(2022,0)B.(1011,1)C.(1011,0)D.(2022,1)
二.填空题(共10小题,满分20分,每小题2分)
11.(2分)(2022春•宝清县期中)如图,动点P在平面直角坐标系xOy中,按图中箭头所示方向运动,第1次从原点到点(1,2),第2次接着运动到点(2,0),第3次接着运动到点(3,1),第4次接着运动到点(4,0)……按这样的运动规律,经过第2023次运动后,动点P的坐标是 .
12.(2分)(2022春•巴东县期末)如图,动点P从(0,2)出发沿所示方向运动,每当碰到长方形的边时反弹,当点P第2022次碰到长方形的边时记为P2022,则点P2022的坐标为 .
13.(2分)(2022春•五华区校级期中)如图,在直角坐标系中,长方形OABC的长为2,宽为1,将长方形OABC沿x轴翻转1次,点A落在A1处,翻转2次,点A落在A2处,翻转3次,点A落在A3处(点A3与点A2重合),翻转4次,点A落在A4处,以此类推…,若翻转2022次,点A落在A2022处,则A2022的坐标为 .
14.(2分)(2022春•九龙坡区校级期中)如图,在平面直角坐标系中,每个小方格的边长为1个单位长度,一只蚂蚁从A1爬到A2,再依次爬到A3,A4……An,其中A1(2,0),A2(1,﹣1),A3(0,0),A4(2,2),则按图中所示规律,A2022的坐标为 .
15.(2分)(2022春•博罗县期末)如图,在平面直角坐标系中,已知正方形ABCD的边长为8,与y轴交于点M(0,5),顶点C(6,﹣3),将一条长为2022个单位长度且没有弹性的细绳一端固定在点M处,从点M出发将细绳紧绕在正方形ABCD的边上,则细绳的另一端到达的位置点N的坐标为 .
16.(2分)(2022春•防城区校级期末)如图,在直角坐标系中,第一次将△OAB变换成△OA1B1,第二次将△OA1B1变换成△OA2B2,第三次将△OA2B2,变换成△OA3B3,已知A(1,3),A1(2,3),A2(4,3),A3(8,3),将△OAB进行n次变换得到△OAnBn,则An( , ).
17.(2分)(2022春•齐齐哈尔期末)如图,在平面直角坐标系中,将边长为1的正方形一边与x轴重合按图中规律摆放,其中相邻两个正方形的间距都是1,点A1(1,0),A2(1,1),A3(2,1),A4(2,0),A5(3,0),A6(3,﹣1),A7(4,﹣1),A8(4,0),A9(5,0)…,则点A2022的坐标为 .
18.(2分)(2022秋•孝南区期末)如图,在平面直角坐标系中,有若干个横纵坐标分别为整数的点,其顺序为(1,0),(2,0),(2,1),(1,1),(1,2),(2,2),…,根据这个规律,第25个点的坐标为 ,第2022个点的坐标为 .
19.(2分)(2022•南京模拟)如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第一次从原点O运动到点P1(1,1),第二次运动到点P2(2,0),第三次运动到P3(3,﹣2),…,按这样的运动规律,第2022次运动后,动点P2022的坐标是 .
20.(2分)(2022春•江岸区校级月考)如图,在平面直角坐标系中,有若干个横坐标,纵坐标均为整数的点.其顺序按图中“→”方向依次排列:(1,0)→(2,0)→(2,1)→(1,1)→(1,2)→(2,2)→…根据这个规律,第87个点的坐标为 ,第2022个点的坐标为 .
三.解答题(共9小题,满分60分)
21.(6分)(2019•涡阳县二模)如图,学校植物园的护栏是由两种大小不等的正方形间隔排列组成,将护栏的图案放在平面直角坐标系中,已知小正方形的边长为1米,则A1的坐标为(2,2)、A2的坐标为(5,2)
(1)A3的坐标为 ,An的坐标(用n的代数式表示)为 .
(2)2020米长的护栏,需要两种正方形各多少个?
22.(6分)(2014春•江岸区期中)在平面直角坐标系中,一蚂蚁从原点O出发,按向上、向右、向下、向右的方向依次不断移动,每次移动1个单位,其行走路线如图所示.
(1)填写下列各点的坐标:A4 ,A8 ;
(2)写出点A4n的坐标(n为正整数);
(3)指出蚂蚁从点A100到点A101的移动方向.
23.(6分)(2022春•芜湖期末)如图,每个小方格边长为1,已知点A1(1,0),A2(1,1),A3(﹣1,1),A4(﹣1,﹣1),A5(2,﹣1),A6(2,2),A7(﹣2,2),A8(﹣2,﹣2),…
(1)将图中的平面直角坐标系补画完整;
(2)按此规律,请直接写出点的坐标:A9,A10;
(3)按此规律,则点A2022的坐标为 .
24.(6分)(2022春•西城区校级期中)在平面直角坐标系中,﹣蚂蚁从原点O出发,按向上、向右、向下、向右的方向依次不断移动,每次移动1个单位.其行走路线如图所示.
(1)填写下列各点的坐标:A4( , ),A8( , );
(2)写出点A4n的坐标(n是正整数)A4n( , );
(3)求出A2022的坐标.
25.(6分)(2020春•船营区期末)在平面直角坐标系中,一只蜗牛从原点O出发,按向上、向右、向下、向右的方向依次不断移动,每次移动1个单位长度,其行走路线如图所示:
(1)填写下列各点的坐标:A5( , ),A9( , ),A13( , );
(2)写出点A4n+1的坐标(n是正整数);
(3)指出蜗牛从点A2020到点A2021的移动方向.
26.(6分)(2018秋•平度市期中)如图,在平面直角坐标系中,第一次将△OAB变换成△OA1B1,第二次将△OA1B1变换成△OA2B2,第三次将OA2B2变换成△OA3B3;已知变换过程中各点坐标分别为A(1,3),A1(2,3),A2(4,3),A3(8,3),B(2,0),B1(4,0),B2(8,0),B3(16,0).
(1)观察每次变换前后的三角形有何变化,找出规律,按此规律再将△OA3B3变换成△OA4B4,则A4的坐标为 ,B4的坐标为 .
(2)按以上规律将△OAB进行n次变换得到△OAnBn,则An的坐标为 ,Bn的坐标为 ;
(3)△OAnBn的面积为 .
27.(8分)(2014春•五莲县校级期中)在平面直角坐标系中,一蚂蚁从原点O出发,按向上、向右、向下、向右的方向依次不断移动,每次移动1个单位.其行走路线如图.
(1)填写下列各点的坐标:A4( , ),A8( , );
(2)点A4n﹣1的坐标(n是正整数)为 ;
(3)指出蚂蚁从点A2013到点A2014的移动方向.
28.(8分)(2013春•建昌县期末)已知:如图,在平面直角坐标系xOy中,横、纵坐标都为整数的点称为整点.观察图中每一个正方形(实践)四条边上的整点的个数.
(1)画出由里向外的第4个正方形,则在第四个正方形上共有 个整点;
(2)请你猜测由里向外第10个正方形(实践)四条边上的整点共有 个.
(3)探究点P(﹣4,4)在第 个正方形的边上,(﹣2n,2n)在第 个正方形的边上(为正整数).
29.(8分)(2012春•洛阳期末)在平面直角坐标系中,一蚂蚁从原点O出发,按向上、向右、向下、向右的方向依次不断移动,每次移动1个单位,其行走路线如图所示.
(1)填写下列各点的坐标:A4( , )A8( , )、A12( , );
(2)写出点A4n的坐标(n是正整数);
(3)指出蚂蚁从点A101到点A102的移动方向.
题号
一
二
三
总分
得分
评卷人
得 分
评卷人
得 分
评卷人
得 分
2022-2023学年人教版七年级数学下册精选压轴题培优卷
专题04 规律型:点的坐标
一.选择题(共10小题,满分20分,每小题2分)
1.(2分)(2022春•江夏区校级月考)如图,长方形BCDE的各边分别平行于x轴或y轴,物体甲和物体乙分别由点A(4,0),F(﹣4,0)同时出发,沿长方形BCDE的边作环绕运动.物体甲按逆时针方向以4个单位/秒匀速运动,物体乙按顺时针方向以2个单位/秒匀速运动,则两个物体运动后的第2022次相遇地点的坐标是( )
A.(2,﹣2)B.(﹣2,﹣2)C.(﹣2,2)D.(2,2)
解:由题意知:矩形的边长为8和4,
①第一次相遇物体甲与物体乙运动的时间为(2+4+4+2)÷(4+2)=2(秒),
∴第一次相遇地点的坐标是(﹣2,2);
②第二次相遇物体甲与物体乙运动的时间为(8×2+4×2)÷(4+2)=4(秒),
∴第二次相遇地点的坐标是(4,0);
③第三次相遇地点的坐标是(﹣2,﹣2);
④第四次相遇地点的坐标是(﹣2,2);
…
则每相遇三次,为一个循环,
∵2022÷3=674,
故两个物体运动后的第2022次相遇地点的坐标为:(﹣2,﹣2),
故答案为:B.
2.(2分)(2022春•惠州期末)如图所示,在平面直角坐标系中,有若干个点按如下规律排列:(1,1),(2,1),(2,2),(3,1),(3,2),(3,3)……,则第50个点的坐标为( )
A.(7,6)B.(8,8)C.(9,6)D.(10,5)
解:设横坐标为n的点的个数为an,横坐标≤n的点的个数为Sn(n为正整数),
观察,发现规律:a1=1,a2=2,a3=3,…,
∴an=n.
S1=a1=1,S2=a1+a2=3,S3=a1+a2+a3=6,…,
∴Sn=1+2+…+n=.
当50≤Sn,即50≤,
解得:n≤﹣(舍去),或n≥.
∵9<<10,
则第50个点的横坐标为10.
故选:D.
(2分)(2022秋•新泰市期末)如图,在平面直角坐标系中,一动点从原点O出发,按向上、向右、向下、向右的方向不断地移动,每移动一个单位,得到点A1(0,1)、A2(1,1)、A3(1,0)、A4(2,0)…,那么点A2022的坐标为( )
A.(1011,0)B.(1011,1)C.(2022,0)D.(2022,1)
解:∵点A1(0,1)、A2(1,1)、A3(1,0)、A4(2,0)、A5(2,1)、A6(3,1)、A7(3,0)、A8(4,0)、A9(4,1)、…,
∴点A4n+2(n为自然数)的坐标为(2n+1,1),
∴点A2022的坐标为(1011,1).
故选:B.
4.(2分)(2022春•高坪区校级月考)一只跳蚤在第一象限及x轴、y轴上跳动,在第一秒钟,它从原点跳动到(0,1),然后接着按图中箭头所示方向跳动[即(0,0)→(0,1)→(1,1)→(1,0)→……],且每秒跳动一个单位,那么第2022秒时跳蚤所在位置的坐标是( )
A.(5,44)B.(2,44)C.(4,45)D.(5,45)
解:由图可得,(0,1)表示1=12秒后跳蚤所在位置;
(0,2)表示8=(2+1)2﹣1秒后跳蚤所在位置;
(0,3)表示9=32秒后跳蚤所在位置;
(0,4)表示24=(4+1)2﹣1秒后跳蚤所在位置;
…,
∴(0,44)表示(44+1)2﹣1=2024秒后跳蚤所在位置,
则(2,44)表示第2022秒后跳蚤所在位置.
故选:B.
5.(2分)(2022春•启东市期中)如图,在平面直角坐标系xOy中,点A坐标是(1,1).若记点A坐标为(a1,a2),则一个点从点A出发沿图中路线依次经过B(a3,a4),C(a5,a6),D(a7,a8)…,每个点的横纵坐标都是整数,按此规律一直运动下去,则a2020+a2021+a2022的值为( )
A.2021B.2022C.1011D.1012
解:由直角坐标系可知A(1,1),B(2,﹣1),C(3,2),D(4,﹣2),
……,
即a1=1,a2=1,a3=2,a4=﹣1,a5=3,a6=2,a7=4,a8=﹣2,
……,
所有数列奇数个都是从1开始逐渐递增的,且都等于所在的个数加上1再除以2,则a2021=1011,
偶数列等于所在的个数除以4,能够整除的,结果的相反数就是所求出的数,不能整除的,等于结果的整数部分加1,且符号为正,
∴a2021=﹣505,2023÷4=505……3,
∴a2022=506,
故 a2020+a2021+a2022=1012,
故选:D.
6.(2分)(2022春•东莞市校级期中)如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2),…,按这样的运动规律,经过第30次运动后,动点P的坐标是( )
A.(30,1)B.(30,0)C.(30,2)D.(31,0)
解:观察点的坐标变化可知:
第1次从原点运动到点(1,1),
第2次接着运动到点(2,0),
第3次接着运动到点(3,2),
第4次接着运动到点(4,0),
第5次接着运动到点(5,1),
…
按这样的运动规律,
发现每个点的横坐标与次数相等,
纵坐标是1,0,2,0,4个数一个循环,
因为30÷4=7……2,
所以经过第30次运动后,
动点P的坐标是(30,0).
故选:B.
7.(2分)(2022春•武昌区期中)如图,动点P从(0,3)出发,沿所示方向运动,每当碰到矩形的边时反弹,反弹时反射角等于入射角(∠AOM=∠BOM),当点P第2022次碰到矩形的边时,点P的坐标为( )
A.(0,3)B.(5,0)C.(1,4)D.(8,3)
解:如图,根据反射角与入射角的定义作出图形,
解:如图,第6次反弹时回到出发点,
∴每6次碰到矩形的边为一个循环组依次循环,
∵2022÷6=337,
∴点P第2022次碰到矩形的边时是第336个循环组的第6次碰边,
坐标为(0,3).
故选:A.
8.(2分)(2022春•突泉县期末)如图,正方形的边长依次为2,4,6,8,……,他们在直角坐标系中的位置如图所示,其中A1(1,1),A2(﹣1,1),A3(﹣1.﹣1),A1(1,﹣1),A5(2.,2),A6(﹣2,2),A7(﹣2,﹣2),A8(2.﹣2),A9(3,3),A10(﹣3,3),……,按此规律接下去,则A2016的坐标为( )
A.(﹣504,﹣504)B.(504,﹣504)
C.(﹣504,504)D.(504,504)
解:∵2016÷4=504,
∴顶点A2016是第504个正方形的顶点,且在第四象限,
横坐标是﹣04,纵坐标是﹣504,
∴A2016(504,﹣504),
故选:B.
9.(2分)(2022春•满城区校级期末)如图,在单位面积为1的方格纸上,A1,A2,A3,A4,A5,…均在格点上,且坐标分别为A1(2,0),A2(1,﹣1),A3(0,0),A4(2,2),A5(4,0),…,则依图中所示规律,点A2022的纵坐标为( )
A.﹣1010B.1010C.﹣1011D.1011
解:观察图形可以看出A1﹣﹣A4;A5﹣﹣﹣A8;…每4个为一组,各三角形都是等腰直角三角形,
∴直角顶点的纵坐标的长度为斜边的一半,
A2(1,﹣1),A6(1,﹣3),A10(1,﹣5)…,…A4n+2(1,﹣(2n+1)),
∵2022÷4=505余2,
∴点A2022在第四象限,横坐标是1,纵坐标是﹣(505×2+1)=﹣1011,
故选:C.
10.(2分)(2022春•合江县期末)在平面直角坐标系中,一个智能机器人接到如下指令:从原点O出发,按向右,向上,向右,向下的方向依次不断移动,每次移动1m,其行走路线如图所示,第一次移动到A1,第二次移动到A2,…,第n次移动到An,则A2022的坐标是( )
A.(2022,0)B.(1011,1)C.(1011,0)D.(2022,1)
解:A1(1,0),A2(1,1),A3(2,1),A4(2,0),A5(3,0),A6(3,1),…,
2022÷4=505……2,
所以A2022的坐标为(505×2+1,1),
则A2021的坐标是(1011,1).
故选:B.
二.填空题(共10小题,满分20分,每小题2分)
11.(2分)(2022春•宝清县期中)如图,动点P在平面直角坐标系xOy中,按图中箭头所示方向运动,第1次从原点到点(1,2),第2次接着运动到点(2,0),第3次接着运动到点(3,1),第4次接着运动到点(4,0)……按这样的运动规律,经过第2023次运动后,动点P的坐标是 (2023,1) .
解:观察图象,结合点P前4次运动后的点的坐标特点可知,各点的横坐标与运动次数相同,而且纵坐标每4次运动组成一个循环:2,0,1,0,
∵2023÷4=505……3,
∴第2023次运动后,动点P的横坐标是2023,纵坐标为1,
故经过第2023次运动后,动点P的坐标是(2023,1),
故答案为:(2023,1).
12.(2分)(2022春•巴东县期末)如图,动点P从(0,2)出发沿所示方向运动,每当碰到长方形的边时反弹,当点P第2022次碰到长方形的边时记为P2022,则点P2022的坐标为 (0,2) .
解:如图所示,
2022÷6=337,
∴点P2022的坐标是(0,2),
故答案为(0,2).
13.(2分)(2022春•五华区校级期中)如图,在直角坐标系中,长方形OABC的长为2,宽为1,将长方形OABC沿x轴翻转1次,点A落在A1处,翻转2次,点A落在A2处,翻转3次,点A落在A3处(点A3与点A2重合),翻转4次,点A落在A4处,以此类推…,若翻转2022次,点A落在A2022处,则A2022的坐标为 (3035,0) .
解:由题意A1(3,2),A2(A3)(5,0),A4(6,1),•••,
发现4次一个循环,
∵2022÷4=,
∴A2022的纵坐标与A2相同,
横坐标=505×6+5=3035,
∴A2022(3035,0),
故答案为:(3035,0).
14.(2分)(2022春•九龙坡区校级期中)如图,在平面直角坐标系中,每个小方格的边长为1个单位长度,一只蚂蚁从A1爬到A2,再依次爬到A3,A4……An,其中A1(2,0),A2(1,﹣1),A3(0,0),A4(2,2),则按图中所示规律,A2022的坐标为 (1,﹣1011) .
解:∵各三角形都是等腰直角三角形,
∴直角顶点的纵坐标的长度为斜边的一半,
A2(1,﹣1),A6(1,﹣3),A10(1,﹣5),……,A4n+2(1,﹣(2n+1)),
∵2022÷4=505余2,
∴点A2022在第三象限,横坐标是1,纵坐标是﹣(505×2+1)=﹣1011,
∴A2002的坐标为(1,﹣1011).
故答案为:(1,﹣1011).
15.(2分)(2022春•博罗县期末)如图,在平面直角坐标系中,已知正方形ABCD的边长为8,与y轴交于点M(0,5),顶点C(6,﹣3),将一条长为2022个单位长度且没有弹性的细绳一端固定在点M处,从点M出发将细绳紧绕在正方形ABCD的边上,则细绳的另一端到达的位置点N的坐标为 (﹣2,1)或(6,5) .
解:∵正方形ABCD的边长为8,
∴CD=DA=BC=AB=8,
∵M(0,5),C(6,﹣3),
∴A(﹣2,5),B(6,5),D(﹣2,﹣3),
∴AM=2,BM=6,
∴绕正方形ABCD一周的细线长度为8×4=32,
∵2022÷32=63…6,
∴细线另一端在绕正方形第64圈的第6个单位长度的位置,
即在AB边或在AD边上,
∴点N的坐标为(﹣2,1)或(6,5).
故答案为:(﹣2,1)或(6,5).
16.(2分)(2022春•防城区校级期末)如图,在直角坐标系中,第一次将△OAB变换成△OA1B1,第二次将△OA1B1变换成△OA2B2,第三次将△OA2B2,变换成△OA3B3,已知A(1,3),A1(2,3),A2(4,3),A3(8,3),将△OAB进行n次变换得到△OAnBn,则An( 2n , 3 ).
解:∵A1的坐标为(2,3),即(21,3);
A2的坐标为(4,3),即(22,3);
A3的坐标为(8,3),即(23,3);
……
∴An的坐标为(2n,3),
故答案为:(2n,3).
17.(2分)(2022春•齐齐哈尔期末)如图,在平面直角坐标系中,将边长为1的正方形一边与x轴重合按图中规律摆放,其中相邻两个正方形的间距都是1,点A1(1,0),A2(1,1),A3(2,1),A4(2,0),A5(3,0),A6(3,﹣1),A7(4,﹣1),A8(4,0),A9(5,0)…,则点A2022的坐标为 (1011,﹣1) .
解:由图可得,第一个正方形中,A1(1,0),A2(1,1),A3(2,1),A4(2,0),
各点的横坐标依次为1,1,2,2,纵坐标依次为0,1,1,0;
第二个正方形中,A5(3,0),A6(3,﹣1),A7(4,﹣1),A8(4,0),
各点的横坐标依次为3,3,4,4,纵坐标依次为0,﹣1,﹣1,0;
根据纵坐标的变化规律可知,每8个点一次循环,
∵2022÷8=,
∴点A2022在第253个循环中的第6个点的位置,故其纵坐标为﹣1,
又∵A5的横坐标为3,A13的横坐标为7,A21的横坐标为11,
…
∴A2021的横坐标为1011,
∴点A2022的坐标为(1011,﹣1),
故答案为:(1011,﹣1).
18.(2分)(2022秋•孝南区期末)如图,在平面直角坐标系中,有若干个横纵坐标分别为整数的点,其顺序为(1,0),(2,0),(2,1),(1,1),(1,2),(2,2),…,根据这个规律,第25个点的坐标为 (5,0) ,第2022个点的坐标为 (45,3) .
解:根据图形,以最外边的矩形边长上的点为准,点的总个数等于x轴上右下角的点的横坐标的平方,
例如:右下角的点的横坐标为1,共有1个,1=12,
右下角的点的横坐标为2时,共有4个,4=22,
右下角的点的横坐标为3时,共有9个,9=32,
右下角的点的横坐标为4时,共有16个,16=42,
…,
右下角的点的横坐标为n时,共有n2个,
①∵52=25,5是奇数,
∴第25个点是(5,0),
②∵452=2025,45是奇数,
∴第2025个点是(45,0),
即第2022个点是(45,3)
故答案为(5,0),(45,3).
19.(2分)(2022•南京模拟)如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第一次从原点O运动到点P1(1,1),第二次运动到点P2(2,0),第三次运动到P3(3,﹣2),…,按这样的运动规律,第2022次运动后,动点P2022的坐标是 (2022,0) .
解:由图形可得,
P点纵坐标的为:1,0,﹣2,0,2,0,1,0,﹣2,0,2,0,…,
循环周期为6,
∵2022÷6=337,
∴P2022的纵坐标是0,在x轴上,
∵P点横坐标的为:1,2,3,4,5,6,7,8,9,10,11,12,…,
∴P2022的横坐标为2022,
∴动点P2022的坐标是(2022,0).
故答案为:(2022,0).
20.(2分)(2022春•江岸区校级月考)如图,在平面直角坐标系中,有若干个横坐标,纵坐标均为整数的点.其顺序按图中“→”方向依次排列:(1,0)→(2,0)→(2,1)→(1,1)→(1,2)→(2,2)→…根据这个规律,第87个点的坐标为 (10,5) ,第2022个点的坐标为 (45,3) .
解:根据图形,以最外边的矩形边长上的点为准,点的总个数等于x轴上右下角的点的横坐标的平方,并且右下角的点的横坐标是奇数时最后以横坐标为该数,纵坐标为0结束,当右下角的点的横坐标是偶数时,以横坐标为1,纵坐标为右下角横坐标的偶数减1的点结束.
例如:右下角的点的横坐标为1,共有1个,1=12,
右下角的点的横坐标为2时,共有4个,4=22,
右下角的点的横坐标为3时,共有9个,9=32,
右下角的点的横坐标为4时,共有16个,16=42,
,
右下角的点的横坐标为9时,共有92=81个,
9是奇数,以横坐标为9,纵坐标为0的点结束,
故第87个点的坐标为(10,5),
右下角的点的横坐标为n时,共有n2个,
∵452=2025,45是奇数,
∴第2025个点是(45,0),
∴第2020个点的坐标为(45,3)
故答案为:(10,5),(45,3).
三.解答题(共9小题,满分60分)
21.(6分)(2019•涡阳县二模)如图,学校植物园的护栏是由两种大小不等的正方形间隔排列组成,将护栏的图案放在平面直角坐标系中,已知小正方形的边长为1米,则A1的坐标为(2,2)、A2的坐标为(5,2)
(1)A3的坐标为 (8,2) ,An的坐标(用n的代数式表示)为 (3n﹣1,2) .
(2)2020米长的护栏,需要两种正方形各多少个?
解:(1)∵A1的坐标为(2,2)、A2的坐标为(5,2),
∴A1,A2,A3,…,An各点的纵坐标均为2,
∵小正方形的边长为1,
∴A1,A2,A3,…,An各点的横坐标依次大3,
∴A3(5+3,2),An(,2),
即A3(8,2),An(3n﹣1,2),
故答案为(8,2);(3n﹣1,2);
(2)∵2020÷3=673…1,
∴需要小正方形674个,大正方形673个.
22.(6分)(2014春•江岸区期中)在平面直角坐标系中,一蚂蚁从原点O出发,按向上、向右、向下、向右的方向依次不断移动,每次移动1个单位,其行走路线如图所示.
(1)填写下列各点的坐标:A4 (2,0) ,A8 (4,0) ;
(2)写出点A4n的坐标(n为正整数);
(3)指出蚂蚁从点A100到点A101的移动方向.
解:(1)由图可知,A4,A8都在x轴上,
∵小蚂蚁每次移动1个单位,
∴OA4=2,OA8=4,
∴A4(2,0),A8(4,0);
故答案为:2,0;4,0;
(2)根据(1)OA4n=4n÷2=2n,
∴点A4n的坐标(2n,0);
(3)∵100÷4=25,
∴100是4的倍数,
∴从点A100到点A101的移动方向与从点O到A1的方向一致,为↑.
23.(6分)(2022春•芜湖期末)如图,每个小方格边长为1,已知点A1(1,0),A2(1,1),A3(﹣1,1),A4(﹣1,﹣1),A5(2,﹣1),A6(2,2),A7(﹣2,2),A8(﹣2,﹣2),…
(1)将图中的平面直角坐标系补画完整;
(2)按此规律,请直接写出点的坐标:A9,A10;
(3)按此规律,则点A2022的坐标为 (506,506) .
解:(1)补画的平面直角坐标系如图所示,
(2)根据图示坐标系各象限横纵坐标符号特点知A9(3,﹣2),A10(3,3),
(3)观察图形发现,下标为4n+2的点落在第一象限的对角线上,
∵A2(1,1),A6(2,2),A10(3,3),…,
∴A4n+2(n+1,n+1).
∵2022=4×505+2,
∴顶点A2022的坐标为(506,506).
故答案为:(506,506).
24.(6分)(2022春•西城区校级期中)在平面直角坐标系中,﹣蚂蚁从原点O出发,按向上、向右、向下、向右的方向依次不断移动,每次移动1个单位.其行走路线如图所示.
(1)填写下列各点的坐标:A4( 2 , 0 ),A8( 4 , 0 );
(2)写出点A4n的坐标(n是正整数)A4n( 2n , 0 );
(3)求出A2022的坐标.
解:观察图形可知,A1( 0,1),A2( 1,1),A3( 1,0),A4( 2,0),A5( 2,1),A6( 3,1),...,A4n( 2n,0),A4n+1( 2n,1),A4n+2( 2n+1,1),A4n+3( 2n+1,0),
(1)根据题意,可直接读出A4( 2,0),A8( 4,0),
故答案为:2,0,4,0;
(2)根据点的坐标规律可知,A4n( 2n,0),
故答案为:2n,0;
(3)∵2022=4×505+2,
∴A2022( 1011,1).
25.(6分)(2020春•船营区期末)在平面直角坐标系中,一只蜗牛从原点O出发,按向上、向右、向下、向右的方向依次不断移动,每次移动1个单位长度,其行走路线如图所示:
(1)填写下列各点的坐标:A5( 2 , 1 ),A9( 4 , 1 ),A13( 6 , 1 );
(2)写出点A4n+1的坐标(n是正整数);
(3)指出蜗牛从点A2020到点A2021的移动方向.
解:(1)根据点的坐标变化可知:
各点的坐标为:A5(2,1),A9(4,1),A13(6,1);
故答案为:2,1,4,1,6,1;
(2)根据(1)发现:
点A4n+1的坐标(n为正整数)为(2n,1);
(3)因为每四个点一个循环,
所以2021÷4=505…1.
所以蜗牛从点A2020到点A2021的移动方向是向上.
26.(6分)(2018秋•平度市期中)如图,在平面直角坐标系中,第一次将△OAB变换成△OA1B1,第二次将△OA1B1变换成△OA2B2,第三次将OA2B2变换成△OA3B3;已知变换过程中各点坐标分别为A(1,3),A1(2,3),A2(4,3),A3(8,3),B(2,0),B1(4,0),B2(8,0),B3(16,0).
(1)观察每次变换前后的三角形有何变化,找出规律,按此规律再将△OA3B3变换成△OA4B4,则A4的坐标为 (16,3) ,B4的坐标为 (32,0) .
(2)按以上规律将△OAB进行n次变换得到△OAnBn,则An的坐标为 (2n,3) ,Bn的坐标为 (2n+1,0) ;
(3)△OAnBn的面积为 3×2n .
解:(1)∵A1(2,3)、A2(4,3)、A3(8,3).
∴A4的横坐标为:24=16,纵坐标为:3.
故点A4的坐标为:(16,3).
又∵B1(4,0)、B2(8,0)、B3(16,0).
∴B4的横坐标为:25=32,纵坐标为:0.
故点B4的坐标为:(32,0).
故答案为:(16,3),(32,0).
(2)由A1(2,3)、A2(4,3)、A3(8,3),可以发现它们各点坐标的关系为横坐标是2n,纵坐标都是3.
故An的坐标为:(2n,3).
由B1(4,0)、B2(8,0)、B3(16,0),可以发现它们各点坐标的关系为横坐标是2n+1,纵坐标都是0.
故Bn的坐标为:(2n+1,0);
故答案为:(2n,3),(2n+1,0);
(3)∵An的坐标为:(2n,3),Bn的坐标为:(2n+1,0),
∴△OAnBn的面积为×2n+1×3=3×2n.
27.(8分)(2014春•五莲县校级期中)在平面直角坐标系中,一蚂蚁从原点O出发,按向上、向右、向下、向右的方向依次不断移动,每次移动1个单位.其行走路线如图.
(1)填写下列各点的坐标:A4( 2 , 0 ),A8( 4 , 0 );
(2)点A4n﹣1的坐标(n是正整数)为 (2n﹣1,1) ;
(3)指出蚂蚁从点A2013到点A2014的移动方向.
解:(1)由图可知,A4,A8都在x轴上,
∵小蚂蚁每次移动1个单位,
∴OA4=2,OA8=4,
∴A4(2,0),A8(4,0);
故答案为:2,0;4,0;
(2)根据(1)OA4n=4n÷2=2n,
∴点A4n﹣1的坐标(2n﹣1,0);
(3)∵2013÷4=503…1,
∴从点A2013到点A2014的移动方向与从点A1到A2的方向一致,为→.
28.(8分)(2013春•建昌县期末)已知:如图,在平面直角坐标系xOy中,横、纵坐标都为整数的点称为整点.观察图中每一个正方形(实践)四条边上的整点的个数.
(1)画出由里向外的第4个正方形,则在第四个正方形上共有 16 个整点;
(2)请你猜测由里向外第10个正方形(实践)四条边上的整点共有 40 个.
(3)探究点P(﹣4,4)在第 8 个正方形的边上,(﹣2n,2n)在第 4n 个正方形的边上(为正整数).
解:(1)由内到外规律,第1个正方形边上整点个数为4×1=4个,
第2个正方形边上整点个数为4×2=8个,第3个正方形边上整点个数为4×3=12,
第4个正方形边上整点个数为4×4=16个;
故答案为:16;
(2)第n个正方形边上的整点个数为4n个,
所以第10个正方形的边上整点个数为4×10=40(个);
故答案为:40;
(3)点P(﹣4,4)在第|﹣4|+|4|=8个正方形的边上,(﹣2n,2n)在第4n个正方形的边上第4n个正方形边上.
故答案为:8,4n.
29.(8分)(2012春•洛阳期末)在平面直角坐标系中,一蚂蚁从原点O出发,按向上、向右、向下、向右的方向依次不断移动,每次移动1个单位,其行走路线如图所示.
(1)填写下列各点的坐标:A4( 2 , 0 )A8( 4 , 0 )、A12( 6 , 0 );
(2)写出点A4n的坐标(n是正整数);
(3)指出蚂蚁从点A101到点A102的移动方向.
解:(1)由图可知,A4,A8,A12都在x轴上,
∵蚂蚁每次移动1个单位,
∴OA4=2,OA8=4,OA12=6,
∴A4(2,0),A8(4,0),A12(6,0);
故答案为:2,0;4,0;6,0;
(2)根据(1)OA4n=4n÷2=2n,
∴点A4n的坐标(2n,0);
(3)∵101÷4=25…1,102÷4=25…2
∴A101与A102的移动方向与从点A1到A2的方向一致,为从左向右
人教版七年级数学下册精选压轴题汇编培优卷专题17不等式(组)的应用(原卷版+解析): 这是一份人教版七年级数学下册精选压轴题汇编培优卷专题17不等式(组)的应用(原卷版+解析),共27页。试卷主要包含了道题?,>11x等内容,欢迎下载使用。
人教版七年级数学下册精选压轴题汇编培优卷专题16一元一次不等式(组)(原卷版+解析): 这是一份人教版七年级数学下册精选压轴题汇编培优卷专题16一元一次不等式(组)(原卷版+解析),共22页。
人教版七年级数学下册精选压轴题汇编培优卷专题06两点间的距离(原卷版+解析): 这是一份人教版七年级数学下册精选压轴题汇编培优卷专题06两点间的距离(原卷版+解析),共21页。












