2024河南中考数学专题复习第三部分 题型二 微专题4 手拉手模型 课件

这是一份2024河南中考数学专题复习第三部分 题型二 微专题4 手拉手模型 课件，共25页。PPT课件主要包含了手拉手模型，解如图连接BD，第6题图，第2题图，第3题图，第4题图，第5题图等内容，欢迎下载使用。

微专题4　手拉手模型(9年6考)
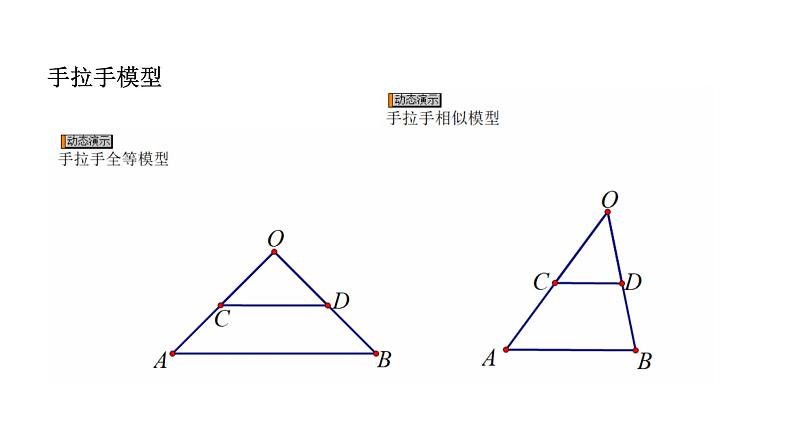
1. (1)OA≠OB，OC≠OD，CD∥AB；(2)∠AOB＝∠COD；(3)将△OCD绕顶点O旋转，连接AC，BD，可得：△AOC∽△BOD.简记：非等腰，共顶角，绕共顶点旋转得相似．
一、手拉手模型动态旋转图形(9年5考)
1. 如图，在Rt△ABC中，∠ABC＝90°，∠ACB＝30°，将△ABC绕点C旋转一定角度得到△A′B′C，求 的值．
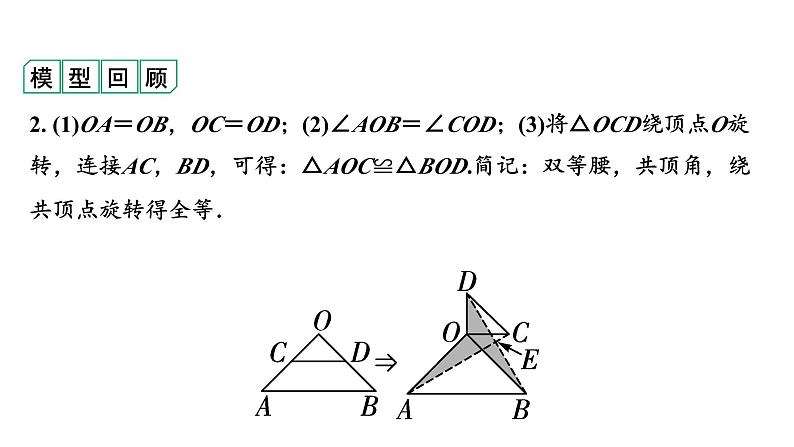
2. (1)OA＝OB，OC＝OD；(2)∠AOB＝∠COD；(3)将△OCD绕顶点O旋转，连接AC，BD，可得：△AOC≌△BOD.简记：双等腰，共顶角，绕共顶点旋转得全等．
2. 如图，将等腰△ABC绕点A旋转得到△DAE，点B，C的对应点分别是点D，E，AB＝AC，连接BD，CE，若BD＝3，求CE的长．
3. 如图，在△ABC中，AC＝BC，∠ACB＝90°，点D是平面内一点，连接DC，DB，将线段DB绕点D逆时针旋转90°得到线段DE，连接AE，BE.求 的值．
二、可视为手拉手模型的静态图形
4. 如图，已知正方形ABCD和正方形DEFG，连接AE，CG相交于点H，AE交CD于点O，试判断AE和CG的数量和位置关系，并证明．
解：AE＝CG，AE⊥CG，证明：∵四边形ABCD与四边形DEFG都为正方形，∴AD＝CD，ED＝GD，∠ADC＝∠EDG＝90°.∴∠ADC＋∠CDE＝∠EDG＋∠CDE，即∠ADE＝∠CDG，
在△ADE和△CDG中，∴△ADE≌△CDG(SAS)，∴AE＝CG，∴∠DAE＝∠DCG，∵∠ADC＝90°，∴∠DAE＋∠AOD＝90°，∵∠AOD＝∠COH，∴∠DCG＋∠COH＝90°，∴∠AHC＝90°，∴AE⊥CG.
5. 如图，在△ABC中，AB＝4，AC＝2 ，P为△ABC内一点，连接BP，CP，且CP⊥BP，延长BP至点D使得∠BAP＝∠CAD，连接CD.若∠APD＝∠ABC，∠DBC＝30°，求AP的长．
设CP＝x，∵CP⊥BP，∠PBC＝30°，∴BC＝2x，BP＝ x，∴ ＝ ＝ ，解得CD＝ x，在Rt△CPD中，根据勾股定理，得PD＝ ＝ x，∵ ＝ ，即 ＝ 解得AP＝ .
6. 如图，将正方形ABCD的边AB绕点A逆时针旋转至AB′，连接BB′，过点D作DE⊥BB′，交BB′的延长线于点E，连接DB′，CE.求 的值．
∵四边形ABCD是正方形，∴ ＝ ，∠BDC＝45°，∴ ＝ ＝ ，∵∠EDB′＝∠BDC，∴∠EDB′－∠B′DC＝∠BDC－∠B′DC，即∠B′DB＝∠EDC，∴△B′DB∽△EDC，∴ ＝ ＝ .
7. 如图，点A是△BCD内一点，∠ADB＝∠ABC＝30°，∠BAC＝90°，BD＝3，CD＝ ，求AD的长．
解：如图，作AE⊥AD，交BD于点E，连接CE，
1. 如图，△ABC中，AD⊥BC于点D，∠ABC＝45°，BC＝4，CD＝1，若将△ADC绕点D逆时针方向旋转得到△FDE，当点E恰好落在AC上时，连接AF.则AF的长是________．
2. 如图，在△ABC中，点D在AB上，过点D作DE∥BC交AC于点E，将△ADE绕点A逆时针旋转，旋转角为α(0°＜α＜180°)，得到△AD′E′，连接CE′，BD′.若AB＝6，AD∶BD＝1∶2，旋转角α＝60°，求BD′的长．
解：如图，过点D′作D′M⊥AB于点M，
3. 如图，在△ABC中，∠BAC＝90°，AB＝AC，点D为BC的中点．若点E，F分别为AB，AC上的点，且DE⊥DF，求证：BE＝AF.
证明：如图，连接AD，
∵∠BAC＝90°，AB＝AC，∴∠C＝∠B＝45°，∵点D为BC的中点，∴AD⊥BC，AD＝BD＝DC，AD平分∠BAC，∴∠DAC＝∠BAD＝∠B＝45°，∠ADC＝90°，∵DE⊥DF，∴∠EDF＝90°，
∴∠ADF＋∠FDC＝90°，∠FDC＋∠BDE＝90°，∴∠BDE＝∠ADF，在△BDE和△ADF中，∴△BDE≌△ADF(ASA)，∴BE＝AF.
4. 如图，在△ABC和△ADE中，∠ABC＝∠ADE＝90°，∠BAC＝∠DAE＝30°，O是BC的中点，连接EO并延长至点F，使得EO＝OF，连接BF，BD，求 的值．
解：如图，连接EC，BE，CF，
∴ ＝ .∵点O是BC的中点，∴OB＝OC，∵OE＝OF，∴四边形BECF是平行四边形，∴BF＝EC，∴ ＝ ＝ .
5. 如图，在Rt△ABC和Rt△ADE中，∠ABC＝∠ADE＝90°，∠ACB＝∠AED，点C，E，D在同一直线上，且AC＝2AE，AB＝3 .(1)求AD的长；