广东省揭阳市普宁二中实验学校2022-2023学年高一（下）期末数学试卷

这是一份广东省揭阳市普宁二中实验学校2022-2023学年高一（下）期末数学试卷，共22页。
2．（5分）在△ABC中，“”是“”的（ ）
A．充分不必要条件
B．必要不充分条件
C．充要条件
D．既不充分也不必要条件
3．（5分）已知复数z1＝（m2﹣1）+（m2+2m﹣3）i，z2＝m+i，其中i为虚数单位，m∈R，若z1为纯虚数，则下列说法正确的是（ ）
A．m＝±1
B．复数z2在复平面内对应的点在第一象限
C．|z2|＝2
D．|z1|2＝|z2|2
4．（5分）在空间中，下列说法正确的是（ ）
A．垂直于同一直线的两条直线平行
B．垂直于同一直线的两条直线垂直
C．平行于同一平面的两条直线平行
D．垂直于同一平面的两条直线平行
5．（5分）有3位男生和2位女生在周日去参加社区志愿活动，从该5位同学中任取3人，至少有1名女生的概率为（ ）
A．B．C．D．
6．（5分）如图所示，△ABC中，点D是线段BC的中点，E是线段AD的靠近A的三等分点，则＝（ ）
A．B．C．D．
7．（5分）已知实数a，b∈（1，+∞），且lg2a+lgb3＝lg2b+lga2，则（ ）
A．B．C．D．
8．（5分）如图（1）所示，已知球的体积为36π，底座由边长为12的正三角形铜片ABC沿各边中点的连线垂直向上折叠成直二面角所得，如图（2）所示．则在图（1）所示的几何体中，下列结论中正确的是（ ）
A．CD与BE是异面直线
B．异面直线AB与CD所成角的大小为45°
C．由A、B、C三点确定的平面截球所得的截面面积为3π
D．球面上的点到底座底面DEF的最大距离为
二．多选题（共4小题，满分20分，每小题5分）
（多选）9．（5分）设复数，则下列命题中正确的是（ ）
A．的虚部是
B．
C．复平面内z与分别对应的两点之间的距离为1
D．
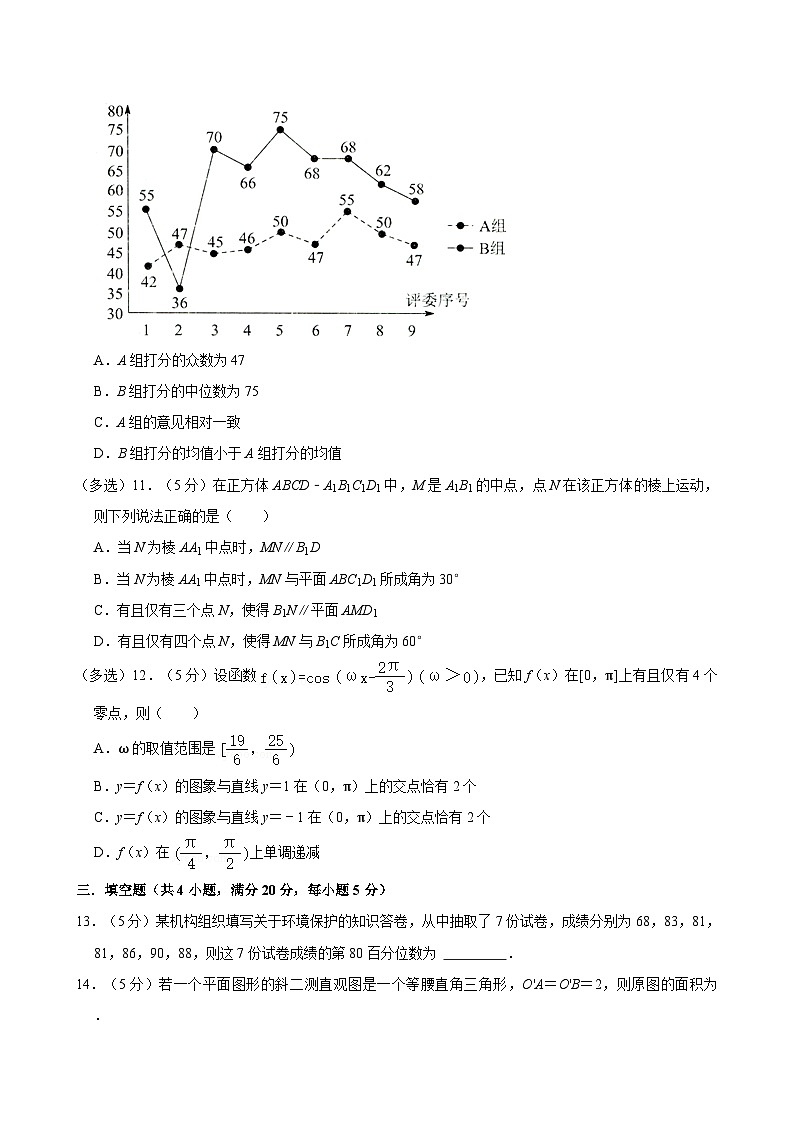
（多选）10．（5分）广东某高校为传承粤语文化，举办了主题为“粤唱粤美好”的校园粤语歌手比赛在比赛中，由A，B两个评委小组（各9人）给参赛选手打分．根据两个评委小组对同一名选手的打分绘制成如图所示折线图，则下列说法正确的是（ ）
A．A组打分的众数为47
B．B组打分的中位数为75
C．A组的意见相对一致
D．B组打分的均值小于A组打分的均值
（多选）11．（5分）在正方体ABCD﹣A1B1C1D1中，M是A1B1的中点，点N在该正方体的棱上运动，则下列说法正确的是（ ）
A．当N为棱AA1中点时，MN∥B1D
B．当N为棱AA1中点时，MN与平面ABC1D1所成角为30°
C．有且仅有三个点N，使得B1N∥平面AMD1
D．有且仅有四个点N，使得MN与B1C所成角为60°
（多选）12．（5分）设函数，已知f（x）在[0，π]上有且仅有4个零点，则（ ）
A．ω的取值范围是
B．y＝f（x）的图象与直线y＝1在（0，π）上的交点恰有2个
C．y＝f（x）的图象与直线y＝﹣1在（0，π）上的交点恰有2个
D．f（x）在上单调递减
三．填空题（共4小题，满分20分，每小题5分）
13．（5分）某机构组织填写关于环境保护的知识答卷，从中抽取了7份试卷，成绩分别为68，83，81，81，86，90，88，则这7份试卷成绩的第80百分位数为 ．
14．（5分）若一个平面图形的斜二测直观图是一个等腰直角三角形，O'A＝O'B＝2，则原图的面积为 ．
15．（5分）已知1+2i是方程x2﹣mx+2n＝0（m，n∈R）的一个根，则m+n＝ ．
16．（5分）《易经》是阐述天地世间关于万象变化的古老经典，如图，这是《易经》中记载的几何图形——八卦图．图中正八边形代表八卦，中间的圆代表阴阳太极图，其余八块面积相等的图形代表八卦图．已知正八边形ABCDEFGH的边长为2，P是正八边形ABCDEFGH所在平面内的一点，则（+）•（+）的最小值为 ．
四．解答题（共6小题，满分70分）
17．（10分）已知复数z＝1+i（i是虚数单位）是方程x2﹣px+q＝0的根，其中p，q是实数．
（1）求p和q的值；
（2）若（p+qi）•（m2+2mi）是纯虚数，求实数m的值．
18．（12分）某校组织高一年级1000名学生参加了跳绳比赛活动，以每个学生的跳绳个数作为最终比赛成绩．现从中随机抽取50名学生的比赛成绩作为样本，整理数据并按比赛成绩[80，100），[100，120），[120，140），[140，160），[160，180），[180，200]分组进行统计，得到比赛成绩的频数分布表，记比赛成绩大于或等于160的为“优秀”．
（1）估计该校高一年级学生比赛成绩为“优秀”的人数；
（2）从样本比赛成绩在[120，140）和[160，180）的学生中随机抽取2人，求两人比赛成绩都为“优秀”的概率．
19．（12分）如图，在四边形OBCD中，，，，且．
（1）用，表示；
（2）点P在线段AC上，且，求与的夹角θ的余弦值．
20．（12分）已知函数的部分图像如图所示．
（1）求函数f（x）的解析式；
（2）将函数f（x）的图像向左平移个单位，再将图像上各点的横坐标伸长到原来的2倍（纵坐标不变）得到函数g（x）的图像，若关于x的方程g（x）﹣m＝0在区间上有两个不同的实数解，求实数m的范围．
21．（12分）在△ABC中，角A，B，C所对的边分别为a，b，c．已知c＝2b，a＝3，D是边BC上一点．
（1）求bcsC+2bcsB的值；
（2）若．
①求证：AD平分∠BAC；
②求△ABC面积的最大值及此时AD的长．
22．（12分）如图，在正四棱锥P﹣ABCD中，PA＝AB＝2，E、F分别为PB、PD的中点，平面AEF与棱PC的交点为G．
（1）求异面直线AE与PF所成角的大小；
（2）求平面AEGF与平面ABCD所成锐二面角的大小；
（3）求点G的位置．
参考答案与试题解析
一．选择题（共8小题，满分40分，每小题5分）
1．（5分）已知集合A＝{y|y＝2x﹣1，x∈Z}，B＝{x|5x2﹣4x﹣1≤0}，则A∩B＝（ ）
A．{1}B．{0，1}C．{0，1，2}D．{1，3，5}
【解答】解：集合A＝{y|y＝2x﹣1，x∈Z}，B＝{x|5x2﹣4x﹣1≤0}＝[﹣，1]，则A∩B＝{1}．
故选：A．
2．（5分）在△ABC中，“”是“”的（ ）
A．充分不必要条件
B．必要不充分条件
C．充要条件
D．既不充分也不必要条件
【解答】解：①在△ABC中，当时，则A＝或，∴充分性不成立，
②当时，则，∴必要性成立，
∴是的必要不充分条件，
故选：B．
3．（5分）已知复数z1＝（m2﹣1）+（m2+2m﹣3）i，z2＝m+i，其中i为虚数单位，m∈R，若z1为纯虚数，则下列说法正确的是（ ）
A．m＝±1
B．复数z2在复平面内对应的点在第一象限
C．|z2|＝2
D．|z1|2＝|z2|2
【解答】解：∵z1＝（m2﹣1）+（m2+2m﹣3）i为纯虚数，
∴，解得m＝﹣1，故A错误，
∴z1＝﹣4i，z2＝﹣1+，
复数z2在复平面内对应的点（﹣1，）在第二象限，故B错误，
|z2|＝，故C正确，
，故D错误．
故选：C．
4．（5分）在空间中，下列说法正确的是（ ）
A．垂直于同一直线的两条直线平行
B．垂直于同一直线的两条直线垂直
C．平行于同一平面的两条直线平行
D．垂直于同一平面的两条直线平行
【解答】解：垂直于同一直线的两条直线的位置关系有：平行、相交和异面，A、B不正确；
平行于同一平面的两条直线的位置关系有：平行、相交和异面，C不正确；
根据线面垂直的性质可知：D正确；
故选：D．
5．（5分）有3位男生和2位女生在周日去参加社区志愿活动，从该5位同学中任取3人，至少有1名女生的概率为（ ）
A．B．C．D．
【解答】解：有3位男生和2位女生在周日去参加社区志愿活动，从该5位同学中任取3人，
基本事件总数n＝＝10，
至少有1名女生包含的基本事件个数m＝＝9．
∴至少有1名女生的概率为P＝＝．
故选：D．
6．（5分）如图所示，△ABC中，点D是线段BC的中点，E是线段AD的靠近A的三等分点，则＝（ ）
A．B．C．D．
【解答】解：由题意可得：＝+，＝，＝+，＝，
∴＝+，
故选：A．
7．（5分）已知实数a，b∈（1，+∞），且lg2a+lgb3＝lg2b+lga2，则（ ）
A．B．C．D．
【解答】解：∵lgb2＜lgb3，
∴lg2a+lgb2＜lg2b+lga2，
即lg2a﹣lga2＜lg2b﹣lgb2，
∵函数在（0，+∞）上单调递增，
∴lg2a＜lg2b，
即a＜b，
故排除选项C、D；
∵lg2b＞lg3b，
∴lg2a+lgb3＞lg3b+lga2，
即lg2a﹣lga2＞lg3b﹣lgb3，
∵函数在（0，+∞）上单调递增，
∴lg2a＞lg3b，
又∵，
∴，
即，
故，
故选：B．
8．（5分）如图（1）所示，已知球的体积为36π，底座由边长为12的正三角形铜片ABC沿各边中点的连线垂直向上折叠成直二面角所得，如图（2）所示．则在图（1）所示的几何体中，下列结论中正确的是（ ）
A．CD与BE是异面直线
B．异面直线AB与CD所成角的大小为45°
C．由A、B、C三点确定的平面截球所得的截面面积为3π
D．球面上的点到底座底面DEF的最大距离为
【解答】解：取DF，EF中点N，M，连接AB，BC，AC，BM，MN，CN，如图，
因△BEF为正三角形，则BM⊥EF，而平面BEF⊥平面DFE，平面BEF∩平面DFE＝EF，BM⊂平面BEF，
于是得BM⊥平面DFE，同理CN⊥平面DFE，即BM∥CN，，
因此，四边形BCNM是平行四边形，有BC∥NM∥DE，则直线CD与BE在同一平面内，故A不正确；
由选项A，同理可得AB∥DF，则异面直线AB与CD所成角等于直线DF与CD所成角60°，故B不正确；
由选项A知，，同理可得AB＝AC＝3，正△ABC外接圆半径，
由A、B、C三点确定的平面截球所得的截面圆是△ABC的外接圆，此截面面积为3π，故C正确；
体积为36π的球半径R，由得R＝3，由选项C知，球心到平面ABC的距离，
由选项A，同理可得点A到平面DFE的距离为，即平面ABC与平面DFE的距离为，
所以球面上的点到底座底面DEF的最大距离为，故D不正确．
故选：C．
二．多选题（共4小题，满分20分，每小题5分）
（多选）9．（5分）设复数，则下列命题中正确的是（ ）
A．的虚部是
B．
C．复平面内z与分别对应的两点之间的距离为1
D．
【解答】解：∵，
∴＝﹣i，
故的虚部是﹣，
故选项A错误；
∵z+＝1，|z|＝＝1，
∴z+＝|z|，
即选项B正确；
复平面内z与分别对应的两点之间的距离为＝，
故选项C错误；
z2+＝（+i）2+﹣i
＝+i﹣+﹣i＝0，
故选项D正确；
故选：BD．
（多选）10．（5分）广东某高校为传承粤语文化，举办了主题为“粤唱粤美好”的校园粤语歌手比赛在比赛中，由A，B两个评委小组（各9人）给参赛选手打分．根据两个评委小组对同一名选手的打分绘制成如图所示折线图，则下列说法正确的是（ ）
A．A组打分的众数为47
B．B组打分的中位数为75
C．A组的意见相对一致
D．B组打分的均值小于A组打分的均值
【解答】解：由折线图可知，小组A打分的分值为：42，47，45，46，50，47，50，47，则小组A打分的分值的众数为47，故选项A正确；
小组B打分的分值按照从小到大排列为：36，55，58，62，66，68，68，70，75中间数为66，故中位数为66，故选项B错误；
小组A的打分成绩比较均匀，波动更小，故A小组意见相对一致，故选项C正确；
小组A的打分分值的均值（42+47+45+46+50+47+50+47 ）×＝46.7，而小组B的打分分值的均值 （55+36+70+66+75+68+68+62+58）×＝62，
所以小组B打分的分值的均值大于小组A打分的分值的均值，故选项D错误．
故选：AC．
（多选）11．（5分）在正方体ABCD﹣A1B1C1D1中，M是A1B1的中点，点N在该正方体的棱上运动，则下列说法正确的是（ ）
A．当N为棱AA1中点时，MN∥B1D
B．当N为棱AA1中点时，MN与平面ABC1D1所成角为30°
C．有且仅有三个点N，使得B1N∥平面AMD1
D．有且仅有四个点N，使得MN与B1C所成角为60°
【解答】解：对于A，∵B1D∩平面A1B1BA＝B1，MN⊂平面 A1B1BA，且B1∉MN，
∴当N为棱AA1中点时，MN与B1D异面，故A错误；
对于B，如图，以D为坐标原点，建立空间直角坐标系，
设AB＝2，则A（2，0，0），B（2，2，0），D1（0，0，2），N（2，0，1），M（2，1，2），
∴＝（0，2，0），＝（﹣2，0，2），＝（0，1，1），
设＝（x，y，z）为平面ABC1D1的法向量，
则，取x＝1，得＝（1，0，1），
记MN与平面ABC1D1所成角为θ，
则sinθ＝＝＝，
∵θ∈[0，]，∴θ＝，故B正确；
对于C，记C1D1中点为N，AB中点为P，连接B1N，B1P，ND，DP，
由正方体性质得DN∥PB1∥AD1，MD1∥DP∥NB1，
又B1N∩DN＝N，MD1∩AD1＝D1，B1N⊂平面B1NDP，DN⊂平面B1NDP，
∴平面B1NDP∥平面AMD1，
∴当点N为C1D1中点或AB中点或与D重合时满足题意，故C正确；
对于D，如图，CD1，B1D1，AC，AB1与B1C的夹角都是60°，
∴当MN与CD1，B1D1，AC，AB1之一平行时，满足题意，
即N为BB1，AA1，A1D1，B1C1中点时，满足题意，故D正确．
故选：BCD．
（多选）12．（5分）设函数，已知f（x）在[0，π]上有且仅有4个零点，则（ ）
A．ω的取值范围是
B．y＝f（x）的图象与直线y＝1在（0，π）上的交点恰有2个
C．y＝f（x）的图象与直线y＝﹣1在（0，π）上的交点恰有2个
D．f（x）在上单调递减
【解答】解：当x∈[0，π]时，ωx﹣∈[﹣，πω﹣]，因为f（x）在[0，π]上有且仅有4个零点，
所以，解得，故A正确；
又由以上分析可知，函数y＝csx在上有且仅有4个零点，
且，则在上，y＝csx出现两次最大值，
此时函数y＝csx的大致图象如图示：
即y＝f（x）在（0，π）上两次出现最大值1，即ωx﹣取0，2π时，y＝f（x）取最大值，
故y＝f（x）的图象与直线y＝1在（0，π）上的交点恰有2个，故B正确；
由于当x∈（0，π）时，ωx﹣∈[﹣，πω﹣]，，
当ωx﹣＝﹣π时，y＝f（x）取最小值﹣1，由于ωx﹣是否取到3π不确定，
故y＝f（x）的图象与直线y＝﹣1在（0，π）上的交点可能是1个或2个，故C错误；
当时，，
因为，所以，，
故的值不一定小于π，
所以f（x）在上不一定单调递减．
故选：AB．
三．填空题（共4小题，满分20分，每小题5分）
13．（5分）某机构组织填写关于环境保护的知识答卷，从中抽取了7份试卷，成绩分别为68，83，81，81，86，90，88，则这7份试卷成绩的第80百分位数为 88 ．
【解答】解：这组数据为68，81，81，83，86，88，90，
因为7×80%＝5.6，所以这7份试卷成绩的第80百分位数为88．
故答案为：88．
14．（5分）若一个平面图形的斜二测直观图是一个等腰直角三角形，O'A＝O'B＝2，则原图的面积为 ．
【解答】解：根据题意，直观图△O'A'B′是一个等腰直角三角形，O'A＝O'B＝2，
则其面积S′＝×2×2＝2，
故原图的面积S＝2S′＝4，
故答案为：4．
15．（5分）已知1+2i是方程x2﹣mx+2n＝0（m，n∈R）的一个根，则m+n＝ ．
【解答】解：将x＝1+2i代入方程x2﹣mx+2n＝0，有（1+2i）2﹣m（1+2i）+2n＝0，
即1+4i﹣4﹣m﹣2mi+2n＝0，即（﹣3﹣m+2n）+（4﹣2m）i＝0，
由复数相等的充要条件，得，解得m＝2，n＝，
故．
故答案为：．
16．（5分）《易经》是阐述天地世间关于万象变化的古老经典，如图，这是《易经》中记载的几何图形——八卦图．图中正八边形代表八卦，中间的圆代表阴阳太极图，其余八块面积相等的图形代表八卦图．已知正八边形ABCDEFGH的边长为2，P是正八边形ABCDEFGH所在平面内的一点，则（+）•（+）的最小值为 ．
【解答】解：如图所示，以该正八边形的中心O为原点，过O与AB平行的直线为x轴，如图建立平面直角坐标系，
再设M，N分别为AB，EF的中点，易知N（），M（0，﹣1），再设P（x，y），
而（+）•（+）＝＝4＝4（）
＝4[]，（当且仅当x＝y＝0取等号），
故所求的最小值为：．
故答案为：．
四．解答题（共6小题，满分70分）
17．（10分）已知复数z＝1+i（i是虚数单位）是方程x2﹣px+q＝0的根，其中p，q是实数．
（1）求p和q的值；
（2）若（p+qi）•（m2+2mi）是纯虚数，求实数m的值．
【解答】解：（1）∵z＝1+i（i是虚数单位）是方程x2﹣px+q＝0的根，
∴也是方程x2﹣px+q＝0的根，
∴，解得p＝q＝2．
（2）由（1）可得，（p+qi）•（m2+2mi）＝（2+2i）•（m2+2mi）＝2m2﹣4m+（4m+2m2）i，
∵（p+qi）•（m2+2mi）是纯虚数，
∴，解得m＝2．
18．（12分）某校组织高一年级1000名学生参加了跳绳比赛活动，以每个学生的跳绳个数作为最终比赛成绩．现从中随机抽取50名学生的比赛成绩作为样本，整理数据并按比赛成绩[80，100），[100，120），[120，140），[140，160），[160，180），[180，200]分组进行统计，得到比赛成绩的频数分布表，记比赛成绩大于或等于160的为“优秀”．
（1）估计该校高一年级学生比赛成绩为“优秀”的人数；
（2）从样本比赛成绩在[120，140）和[160，180）的学生中随机抽取2人，求两人比赛成绩都为“优秀”的概率．
【解答】解：（1）由频数分布表可知，样本比赛成绩大于或等于160的学生有3+15＝18人，所以估计该校高一年级学生比赛成绩为“优秀”的人数为1000×＝360人；
（2）设“两人比赛成绩都为‘优秀’”为事件M，
记比赛成绩在[120，140）的学生为A1，A2，比赛成绩在[160，180）的学生为B1，B2，B3，
则从这5个学生中随机抽取2人的样本空间Ω＝{（A1，A2），（A1，B1），（A1，B2），（A1，B3），（A2，B1），（A2，B2），（A2，B3），（B1，B2），（B1，B3），（B2，B3）}，
M＝{（B1，B2），（B1，B3），（B2，B3）}，
所以，由古典概型得P（M）＝；
综上，估计该校高一年级学生比赛成绩为“优秀”的人数为360，两人比赛成绩都为优秀的概率为．
19．（12分）如图，在四边形OBCD中，，，，且．
（1）用，表示；
（2）点P在线段AC上，且，求与的夹角θ的余弦值．
【解答】解：（1）＝++＝﹣+2+＝﹣+2；
（2）＝+，＝＝+＝+，
＝﹣，＝+＝﹣++＝﹣，
•＝（﹣+2）•（﹣）＝+×4＝，
||＝＝，||＝＝．
cs＜，＞＝＝．
20．（12分）已知函数的部分图像如图所示．
（1）求函数f（x）的解析式；
（2）将函数f（x）的图像向左平移个单位，再将图像上各点的横坐标伸长到原来的2倍（纵坐标不变）得到函数g（x）的图像，若关于x的方程g（x）﹣m＝0在区间上有两个不同的实数解，求实数m的范围．
【解答】解：（1）由已知函数f（x）＝（ω＞0，|φ|＜）的部分图象得，
解得，
∴；
（2）由题意可知，g（x）＝，
g（x）﹣m＝0在区间上有两个不同的实数解，
则直线y＝m与函数g（x）＝有两个不同的交点，
令，
则g（x）对称轴为x＝，
∵，
∴当k＝0，x＝符合题意，即两个交点关于x＝对称，
∴，g（0）＝1，
∴m的取值范围为[1，）．
21．（12分）在△ABC中，角A，B，C所对的边分别为a，b，c．已知c＝2b，a＝3，D是边BC上一点．
（1）求bcsC+2bcsB的值；
（2）若．
①求证：AD平分∠BAC；
②求△ABC面积的最大值及此时AD的长．
【解答】解：（1）因为c＝2b，a＝3，
所以bcsC+2bcsB＝bcsC+ccsB＝b•+c•＝＝a＝3，
所以bcsC+2bcsB的值为3；
（2）①证明：因为，所以，
由a＝3知，BD＝2，DC＝1，
设∠BAD＝α，∠DAC＝β，∠ADB＝θ，
在△ABD中，由正弦定理得，＝，
即＝，所以sinα＝，
在△ACD中，由正弦定理得，＝，
即＝，所以sinβ＝，
所以sinα＝sinβ，即∠BAD＝∠DAC，所以AD平分∠BAC，
②在△ABC中，因为c＝2b，a＝3，
由余弦定理a2＝b2+c2﹣2bccsA得，9＝b2（5﹣4csA），
而△ABC的面积S＝bcsinA＝b2sinA；
由9＝b2（5﹣4csA）得csA＝，
所以S＝b2sinA＝b2＝b2＝•，
所以当b2＝5即时，面积S最大为3，
此时在△ABC中，a＝3，b＝，c＝2，
所以由余弦定理求得csC＝＝﹣，
，
在△ADC中，由余弦定理得AD2＝AC2+DC2﹣2AC•DCcsC＝8，
所以此时AD＝2．
22．（12分）如图，在正四棱锥P﹣ABCD中，PA＝AB＝2，E、F分别为PB、PD的中点，平面AEF与棱PC的交点为G．
（1）求异面直线AE与PF所成角的大小；
（2）求平面AEGF与平面ABCD所成锐二面角的大小；
（3）求点G的位置．
【解答】解：（1）连接AC，BD，相交于点O，
因为四边形ABCD是正方形，所以O是正方形的中心，连接PO，
因为四棱锥P﹣ABCD是正四棱锥，则PO⊥底面ABCD，连接OE，
因为E为PB的中点，所以EO是△PBD的中位线，所以EO∥PD，
∠OEA（或补角）即为异面直线AE与PF所成角的大小，
因为正四棱锥P﹣ABCD中，，所以△PAB是等边三角形，
所以，由勾股定理得：，所以AO＝2，
因为PO⊥BD，E为PB的中点，所以，
在△AOE中，由余弦定理得：，
所以异面直线AE与PF所成角的大小为．
（2）连接EF，与OP相交于点Q，则Q为OP，EF的中点，
因为EF分别为PBPD的中点，所以EF是三角形PBD的中位线，所以EF∥BD，
因为BD⊂平面ABCD，EF⊄平面ABCD，所以EF∥平面ABCD，
设平面AEGF与平面ABCD相交于直线l，故EF∥l∥DB，连接QA，
则因为AE＝AF，所以AQ⊥EF，又因为OA⊥BD，
故∠QAO即为平面AEGF与平面ABCD所成锐二面角，其中，AO＝2，
所以，故，
即平面AEGF与平面ABCD所成锐二面角的大小为．
（3）延长AQ，则由两平面相交的性质可得AQ一定过点G，
过点G作GM∥PO交AC于点M，因为PO⊥底面ABCD，所以GM⊥底面ABCD，
设GM＝CM＝x，则AM＝4﹣x，由第二问知：，
所以，即，解得：，
故，所以点G的位置为线段PC靠近P的三等分点．
比赛成绩
[80，100）
[100，120）
[120，140）
[140，160）
[160，180）
[180，200]
人数
4
10
2
16
3
15
比赛成绩
[80，100）
[100，120）
[120，140）
[140，160）
[160，180）
[180，200]
人数
4
10
2
16
3
15