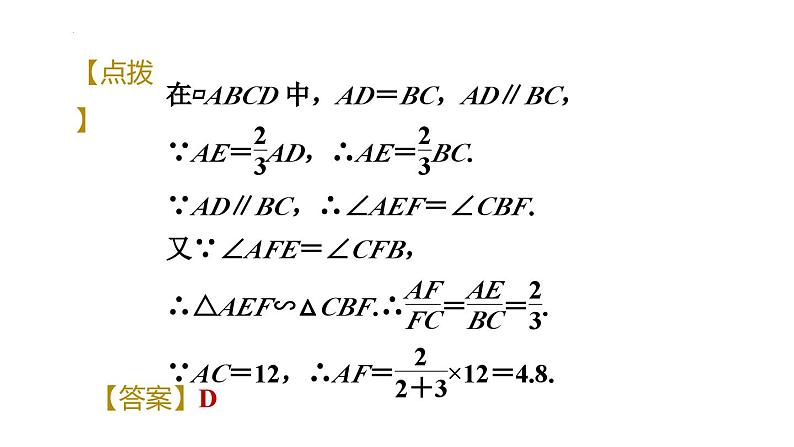
第4章 相似三角形专题七　相似三角形中的基本模型课件浙教版数学九年级上册

这是一份第4章 相似三角形专题七　相似三角形中的基本模型课件浙教版数学九年级上册，共52页。PPT课件主要包含了母题1，方法点拨，变式1-1，变式1-2，答案D，母题2，变式2-1，母题3，变式3-1，母题4等内容，欢迎下载使用。

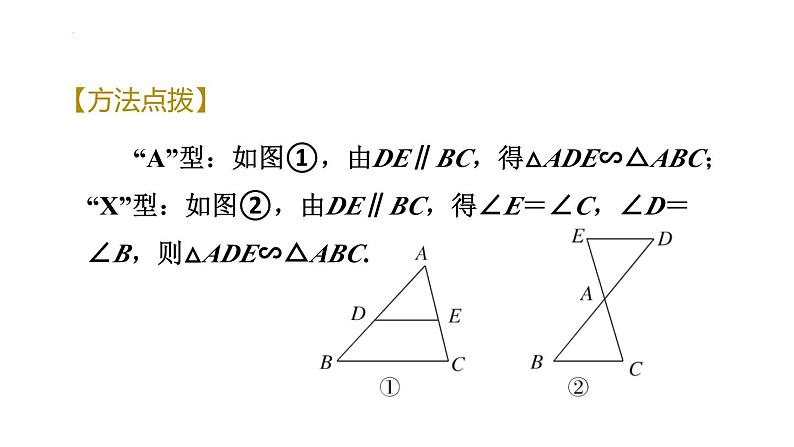
“A”型：如图①，由DE∥BC，得△ADE∽△ABC；“X”型：如图②，由DE∥BC，得∠E＝∠C，∠D＝∠B，则△ADE∽△ABC.
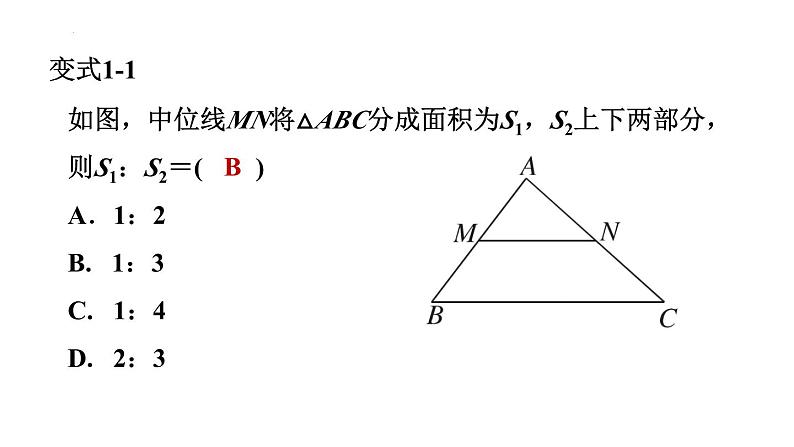
如图，中位线MN将△ABC分成面积为S1，S2上下两部分，则S1：S2＝(　　)A．1：2B. 1：3C. 1：4D. 2：3
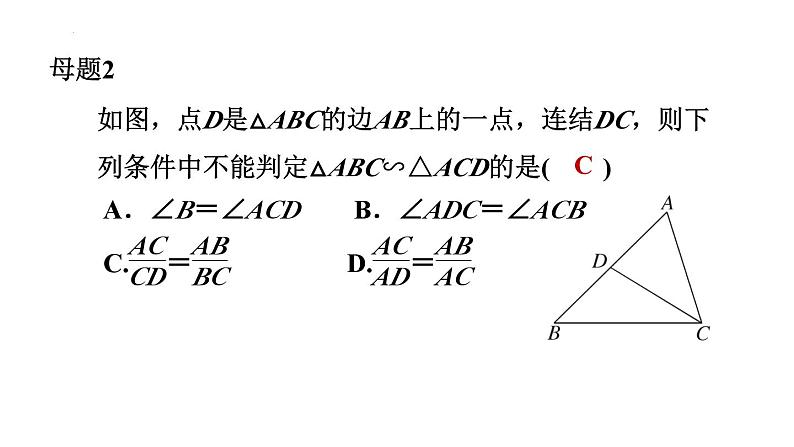
如图，点D是△ABC的边AB上的一点，连结DC，则下列条件中不能判定△ABC∽△ACD的是(　　)
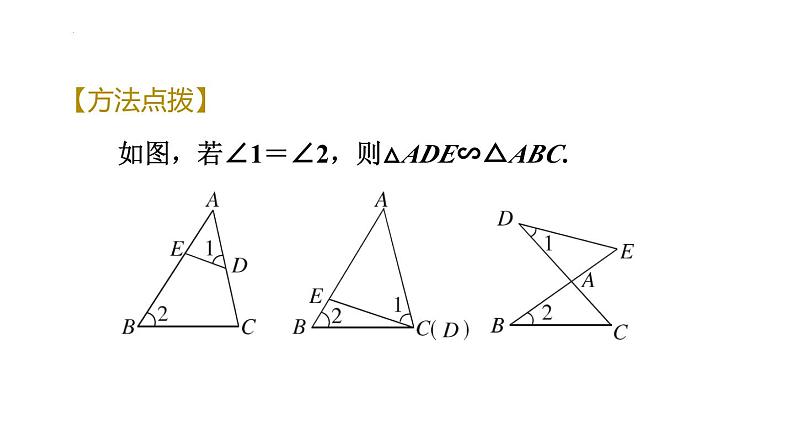
如图，若∠1＝∠2，则△ADE∽△ABC.
如图，已知∠1＝∠2，要使得△ABD∽△CBE，还需添加什么条件？
解：∠BAD＝∠BCE(答案不唯一)．
如图，已知∠1＝∠2，可得∠B′A′C′＝∠BAC，需找另一组角对应相等或夹∠B′A′C′与∠BAC的两边对应成比例．
【2023·邵阳】如图，CA⊥AD，ED⊥AD，点B是线段AD上的一点，且CB⊥BE.已知AB＝8，AC＝6，DE＝4.(1)求证：△ABC∽△DEB；
证明：∵AC⊥AD，ED⊥AD，∴∠A＝∠D＝90°.∴∠C＋∠ABC＝90°.∵CB⊥BE，∴∠ABC＋∠EBD＝90°.∴∠C＝∠EBD.∴△ABC∽△DEB.
(2)求线段BD的长．
如图，点C在边BE上，若∠B＝∠ACD＝∠E，则△ABC∽△CED.
如图，在正方形ABCD中，E为BC上任意一点(与B，C不重合)，∠AEF＝90°.(1)如图①，△ABE与△ECF是否相似？证明你的结论．
解：相似．证明如下：∵四边形ABCD是正方形，∴∠B＝∠C＝90°.∴∠BAE＋∠AEB＝90°.∵∠AEF＝90°.∴∠AEB＋∠CEF＝90°.∴∠BAE＝∠CEF.∴△ABE∽△ECF.
(2)如图②，若E为BC的中点，连结AF，图中有哪些相似三角形？请证明．
如图，在△ABC中，AB＝AC，点E在边BC上移动(点E不与点B，C重合)，点D，F分别在边AB，AC上，且满足∠DEF＝∠B.(1)求证：△BDE∽△CEF；
证明：∵AB＝AC，∴∠B＝∠C.∵∠BDE＝180°－∠B－∠DEB，∠CEF＝180°－∠DEF－∠DEB，且∠DEF＝∠B，∴∠BDE＝∠CEF.∴△BDE∽△CEF.
(2)当点E移动到BC的中点时，求证：FE平分∠DFC.
在△ABC中，D，E分别在边AB，AC上，DE∥BC，AD＝4，DB＝2，DE＝3.5，则BC的长度为(　　)A．5.5 B．5.25 C．6.5 D．7
如图，AD与BC交于点O，∠D＝∠B，OA：OC＝3：2，△OAB与△OCD的面积分别是S1与S2，周长分别是C1与C2，则下列选项正确的是(　　)
【2023·绍兴柯桥区期中】如图，∠1＝∠2，则下列各式中，不能说明△ABC∽△ADE的是(　　)
如图，在△ABC中，CH⊥AB，CH＝5，AB＝10，四边形DEFG是矩形，DE在AB边上，DG：GF＝1：2，则△GFC与△ABC的面积比为(　　)
【2023·陕西】如图，DE是△ABC的中位线，点F在DB上，DF＝2BF.连结EF并延长，与CB的延长线相交于点M.若BC＝6，则线段CM的长为(　　)
【2024·宁波期末】在△ABC中，AB＝4，AC＝6，已知点D为AB的中点，点E在线段AC上，连结DE，若△ABC与△ADE相似，则AE的长为________．
【2024·杭州模拟】如图，AD和BE都是△ABC的高，相交于点F，连结DE.(1)求证：△CAB∽△CDE；
(2)若点D是BC的中点，CE＝6，BE＝8，则AB的长为________．
【2024·绍兴期末】如图，在△ABC中，点D，E分别在边AC，AB上，且AE·AB＝AD·AC，连结DE，BD.(1)求证：△ADE∽△ABC.
(2)若点E为AB的中点，ADAE＝65，△ABC的面积为50，求△BCD的面积．
【问题背景】如图①，已知△ABC∽△ADE，求证：△ABD∽△ACE；
如图，过点A作AB的垂线，过点D作AD的垂线，两垂线交于点M，连结BM.∵∠BAM＝90°，∠BAD＝30°，∴∠DAM＝60°.又∵∠ADM＝90°，