2024年上海市宝山区中考数学二模试卷（含解析）

这是一份2024年上海市宝山区中考数学二模试卷（含解析），共21页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

1.若二次根式 x−1有意义，则x的取值范围为( )
A. x≥1B. x≥0C. x>1D. x>0
2.若关于x的一元二次方程x2−x−m=0有两个相等实数根，则实数m的值为( )
A. −14B. −4C. 14D. 4
3.下列函数中，y的值随x值的增大而减小的是( )
A. y=2x2+1B. y=−2x2+1C. y=x+1D. y=−x+1
4.连续两次掷一枚质地均匀的硬币，两次都是正面朝上的概率是( )
A. 16B. 14C. 13D. 12
5.上海发布微信公众号可查询到上海市实时空气质量状况.下面是三月某一周连续七天的空气质量指数(AQI)：28，26，26，37，33，40，117，这组数据的下列统计量中，能比较客观地反映这一周空气质量平均水平的是( )
A. 平均数B. 中位数C. 众数D. 方差
6.如图，△ABC中，∠C=90°，AB=5，tanB=12，如果以点C为圆心，半径为R的⊙C与线段AB有两个交点，那么⊙C的半径R的取值范围是( )
A. 2B. 2≤R≤ 5
C. 5≤R≤2 5
D. 0二、填空题：本题共12小题，每小题4分，共48分。
7.a6÷a2=______．
8.因式分解：m2−3m= ______．
9.不等式x−12<0的解集是______．
10.方程 2−x=−x的解是______．
11.我国天文学家算出了仙女星系“体重”.仙女星系是距离银河系最近的大型漩涡星系，是研究星系形成和演化的绝佳案例.计算得到仙女星系质量约为11400亿倍太阳质量.把数据11400亿用科学记数法表示应是______．
12.某厂生产了1000只灯泡.为了解这1000只灯泡的使用寿命，从中随机抽取了50只灯泡进行检测，结果有28只灯泡的使用寿命超过了2500小时，那么估计这1000只灯泡中使用寿命超过2500小时的灯泡的数量为______只.
13.《孙子算经》记载了这样一个题目：今有木，不知长短.引绳度之，余绳四尺五寸；屈绳量之，不足一尺.木长几何？其大意是：用一根绳子去量一根长木，绳子还剩余4.5尺；将绳子对折再量长木，长木多出1尺.那么长木的长度为______尺.
14.如图，街心花园有A、B、C三座小亭子，A、C两亭被池塘隔开，A、B、C三亭所在的点不共线.设AB、BC的中点分别为M、N.如果MN=3米，那么AC= ______米.
15.如图，正六边形ABCDEF，连接OE、OD，如果OD=a,OE=b，那么AB= ______．
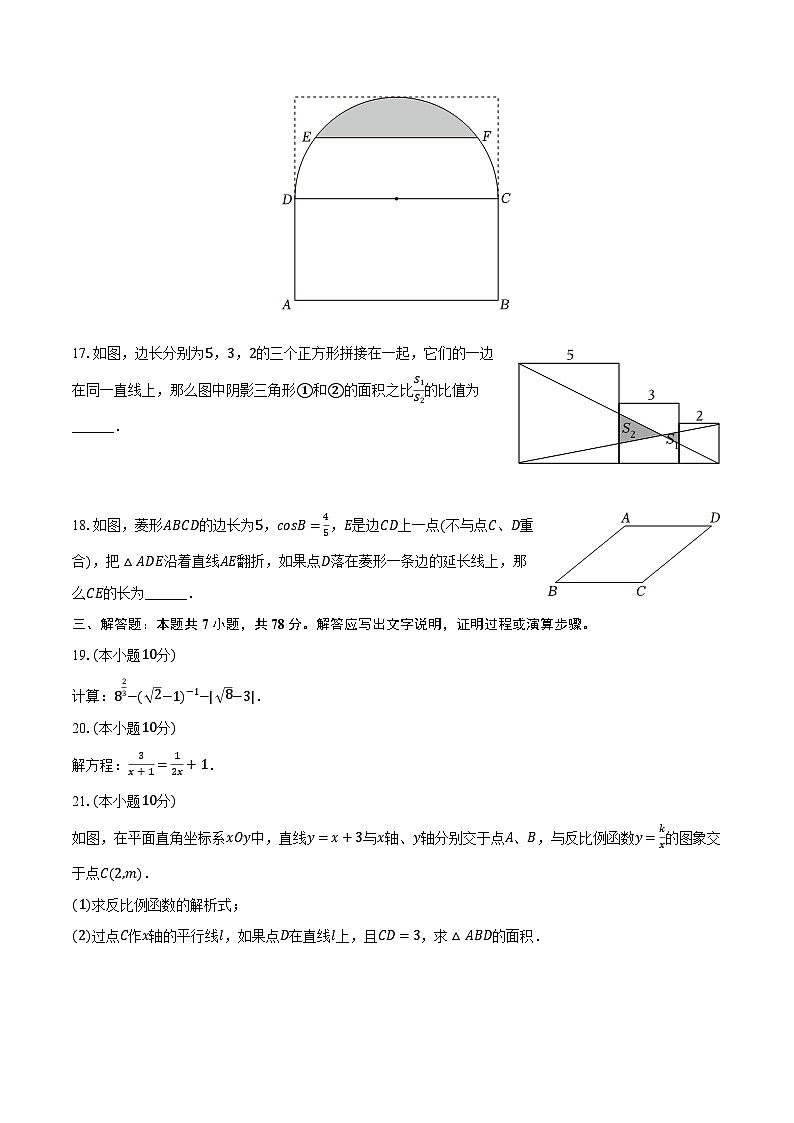
16.为传承海派文化，社区准备举办沪剧爱好者观摩演出活动.把某场馆的一个正方形区域改造成一个由矩形和半圆形组成的活动场地(如图)，矩形ABCD是观众观演区，阴影部分是舞台，CD是半圆O的直径，弦EF与CD平行.已知EF长8米，舞台区域最大深度为2米，如果每平方米最多可以坐3名观众，那么观演区可容纳______名观众．
17.如图，边长分别为5，3，2的三个正方形拼接在一起，它们的一边在同一直线上，那么图中阴影三角形①和②的面积之比S1S2的比值为______．
18.如图，菱形ABCD的边长为5，csB=45，E是边CD上一点(不与点C、D重合)，把△ADE沿着直线AE翻折，如果点D落在菱形一条边的延长线上，那么CE的长为______．
三、解答题：本题共7小题，共78分。解答应写出文字说明，证明过程或演算步骤。
19.(本小题10分)
计算：823−( 2−1)−1−| 8−3|．
20.(本小题10分)
解方程：3x+1=12x+1．
21.(本小题10分)
如图，在平面直角坐标系xOy中，直线y=x+3与x轴、y轴分别交于点A、B，与反比例函数y=kx的图象交于点C(2,m)．
(1)求反比例函数的解析式；
(2)过点C作x轴的平行线l，如果点D在直线l上，且CD=3，求△ABD的面积．
22.(本小题10分)
小明家院内靠墙安装了一个遮阳篷(如图1)，图2是它的侧面示意图，遮阳篷长AC=6米，与水平面的夹角为17.5°，靠墙端A离地高度AB=5米，已知该地区冬至正午太阳光照入射角∠CDF=36.9°，夏至正午太阳光照入射角∠CEF=82.4°，因此，点D、E之间的区域是一年四季中阳光不一定照射到的区域，求该区域深度DE的长.(结果精确到0.1米)
参考数据：sin17.5°≈0.3，cs17.5°≈0.95，tan17.5°≈0.32；sin36.9°≈0.6，cs36.9°≈0.8，tan36.9°≈0.75；sin82.4°≈0.99，cs82.4°≈0.13，tan82.4°≈7.5．
23.(本小题12分)
如图，在⊙O中，直径AB垂直于弦CD，垂足为点E，联结AC、DO，延长DO交AC于点F．
(1)求证：AF2=OF⋅DF；
(2)如果CD=8，BE=2，求OF的长．
24.(本小题12分)
在平面直角坐标系xOy中(如图)，已知开口向下的抛物线y=ax2−2x+4经过点P(0,4)，顶点为A．
(1)求直线PA的表达式；
(2)如果将△POA绕点O逆时针旋转90°，点A落在抛物线上的点Q处，求抛物线的表达式；
(3)将(2)中得到的抛物线沿射线PA平移，平移后抛物线的顶点为B，与y轴交于点C.如果PC= 2AB，求tan∠PBC的值．
25.(本小题14分)
已知AB是半圆O的直径，C是半圆O上不与A、B重合的点，将弧AC沿直线AC翻折，翻折所得的弧交直径AB于点D，E是点D关于直线AC的对称点．
(1)如图，点D恰好落在点O处．
①用尺规作图在图中作出点E(保留作图痕迹)，联结AE、CE、CD，求证：四边形ADCE是菱形；
②联结BE，与AC、CD分别交于点F、G，求FGBE的值；
(2)如果AB=10，OD=1，求折痕AC的长．
答案和解析
1.【答案】A
【解析】解：∵二次根式 x−1有意义，
∴x−1≥0，
解得：x≥1．
故选：A．
直接利用二次根式有意义的条件分析得出答案．
此题主要考查了二次根式有意义的条件，正确把握定义是解题关键．
2.【答案】A
【解析】解：∵一元二次方程x2−x−m=0有两个相等的实数根，
∴Δ=0，
∴12−4×1×(−m)=0，
解得m=−14，
故选：A．
利用方程有两个相等的实数根，得到Δ=0，建立关于m的方程，解答即可．
此题考查利用一元二次方程的根的情况求参数，一元二次方程的根有三种情况：有两个不等的实数根时Δ>0；当一元二次方程有两个相等的实数根时，Δ=0；当方程没有实数根时，Δ<0，正确掌握此三种情况是正确解题的关键．
3.【答案】D
【解析】解：由题意，对于A选项，y=2x2+1是二次函数，对称轴是y轴，开口向上，
∴当x<0时，y随x的增大而减小，当x>0时，y随x的增大而增大，故A错误．
对于B选项，y=−2x2+1是二次函数，对称轴是y轴，开口向上，
∴当x<0时，y随x的增大而增大，当x>0时，y随x的增大而减小，故B错误．
对于C选项，y=x+1是一次函数，k=1>0，
∴y随x的增大而增大，故C错误．
对于D选项，y=−x+1是一次函数，k=−1<0，
∴y随x的增大而减小，故D正确．
故选：D．
依据题意，由二次函数的图象与性质、一次函数的图象与性质分别进行判断可以得解．
本题主要考查了二次函数的性质及一次函数的性质，解题时要熟练掌握并理解其增减性是关键
4.【答案】B
【解析】【分析】
画树状图展示所有4种等可能的结果数，再找出两次都是“正面朝上”的结果有1种，然后根据概率公式求解．
此题考查的是画树状图法求概率．树状图法可以不重复不遗漏的列出所有可能的结果，适合两步或两步以上完成的事件；用到的知识点为：概率=所求情况数与总情况数之比．
【解答】
解：画树状图如下：
共有4种等可能的结果数，其中两次都是“正面朝上”的结果有1种，
∴两次都是“正面朝上”的概率=14，
故选：B．
5.【答案】B
【解析】解：这组数据的平均数为28+26+26+37+33+40+1177=3077，中位数为33，众数为26，方差是反应数据的集中趋势的统计量，
所以能比较客观地反映这一周空气质量平均水平的是中位数，
故选：B．
这组数据的平均数受极端数值117影响，众数偏离大多数据，方差是反应数据的集中趋势的统计量，据此可得答案．
本题主要考查统计量的选择，解题的关键是掌握平均数、中位数、众数及方差的意义．
6.【答案】A
【解析】解：∵∠C=90°，tanB=12，
∴ACBC=12，
设AC=x，BC=2x，
∴AB= AC2+BC2= 5x=5，
∴x= 5，
∴AC= 5，BC=2 5，
过点C作CD⊥AB于点D，
∴CD=AC⋅BCAB=2，
∵⊙C与线段AB有两个交点，
∴2故选：A．
根据直线与圆的位置关系得出相切时有两个交点，再结合图形得出另一种有一个交点的情况，即可得出答案．
此题主要考查了直线与圆的位置关系，熟练掌握切线的性质是解题的关键．
7.【答案】a4
【解析】【分析】
根据同底数幂的除法，可得答案．
本题考查了同底数幂的除法，同底数幂的除法底数不变指数相减．
【解答】
解：a6÷a2=a4．
故答案为：a4．
8.【答案】m(m−3)
【解析】解：m2−3m=m(m−3)．
故答案为：m(m−3)．
直接找出公因式m，进而分解因式得出答案．
此题主要考查了提取公因式法分解因式，正确找出公因式是解题关键．
9.【答案】x≤1
【解析】解：去分母，得x−1≤0．
移项，得x≤1．
根据不等式的性质：先分母，再移项，合并同类项即可．
本题考查解一元一次不等式，解题的关键是掌握不等式的基本性质，能求一元一次不等式的解集．
10.【答案】x=−2．
【解析】解：对于方程 2−x=−x，两边同时平方得：2−x=x2，
移项得：x2+x−2=0，
∴(x−1)(x+2)=0，
∴x−1=0或x+2=0，
由x−1=0，解得：x=1，
由x+2=0，解得：x=−2，
经检验得：x=1为增根，x=−2是原方程的根．
∴方程 2−x=−x的解是x=−2．
故答案为：x=−2．
首先将两边同时平方得2−x=x2，再解这个整式方程求出x，然后再进行检验即可得出原方程的解．
此题主要考查了解无理方程，熟练掌握解无理方程的一般方法是解决问题的关键．
11.【答案】1.14×1012
【解析】解：11400亿=1140000000000=1.14×1012，
故答案为：1.14×1012．
将一个数表示成a×10n的形式，其中1≤|a|<10，n为整数，这种记数方法叫做科学记数法，据此即可求得答案．
本题考查科学记数法表示较大的数，熟练掌握其定义是解题的关键．
12.【答案】560
【解析】解：(28÷50)×1000=560(只)
故答案为：560．
先求出调查中使用寿命超过了2500小时的灯泡占比，再用占比乘总数，即可求解．
本题考查了用样本估计总体，理清题目的数量关系并仔细计算是解题关键．
13.【答案】6.5
【解析】解：设木长为x尺，
根据题意得：12(x+4.5)=x−1，
解得x=6.5，
答：木长6.5尺．
故答案为：6.5．
设木长x尺，则绳子长为(x+4.5)尺，再由将绳子对折再量长木，长木还剩余1尺列出方程求解即可．
本题主要考查了一元一次方程的实际应用，读懂题意，找到等量关系列方程是解题的关键．
14.【答案】6
【解析】解：∵点M、N分别为AB、BC的中点，
∴MN是△ABC的中位线，
∴AC=2MN=2×3=6(米)，
故答案为：6．
根据三角形中位线定理计算即可．
本题考查的是三角形中位线定理，熟记三角形中位线等于第三边的一半是解题的关键．
15.【答案】a−b
【解析】解：如图所示，连接BD，
由题意得，AB=DE=BC=CD，∠ABC=∠C=∠CDE=180°×(6−2)6=120°，
∴∠CBD=∠CDB=30°，
∴∠ABD=∠BDE=90°，
∴∠ABD+∠BDE=180°，
∴AB//DE，
∴AB=ED，
∵OD=a,OE=b，
∴AB=ED=OD−OE=a−b．
故答案为：a−b．
连接BD，先由正六边形的性质可得AB=DE=BC=CD，∠ABC=∠C=∠CDE=120°，进而求出∠ABD=∠BDE=90°，则可证明AB//DE，得到AB=ED，则AB=ED=OD−OE=a−b．
本题主要考查了平面向量，平行线的性质与判定，正多边形内角和定理，等边对等角等等．
16.【答案】150
【解析】解：设半圆的圆心为O，过点O作OH⊥EF于点H，交⊙O于点J，连接OE．
设OE=OJ=r米，
∵OH⊥EF，
∴EH=FH=12EF=4(米)，
在Rt△OEH中，OE2=EH2+OH2，
∴r2=42+(r−2)2，
∴r=5，
∴AB=CD=10，AD=BC=5，
∴矩形ABCD的面积=5×10=50(平方米)，
∵每平方米最多可以坐3名观众，
∴观演区可容纳150名观众．
故答案为：150．
设半圆的圆心为O，过点O作OH⊥EF于点H，交⊙O于点J，连接OE.利用垂径定理，勾股定理求出半径，再求出矩形ABCD的面积，可得结论．
本题考查垂径定理的应用，勾股定理等知识，解题的关键是理解题意，学会添加常用辅助线，构造直角三角形解决问题．
17.【答案】425
【解析】解：设AH分别交CD、FG、BM于点K、I、L，BM分别交CD、FG于点P、Q，设AH=m，
∵正方形ABCD、正方形CEFG和正方形GHMN的一边在同一条直线上，
∴∠ABC=∠DCG=∠FGH=∠MHG=90°，AB=BC=AD=5，CG=EF=3，GH=HM=MN=2，
∴AB//CD//FG//MH，BH=5+3+2=10，HC=3+2=5，
∵HM//AB，
∴△HLM∽△ALB，
∴HLAL=HMAB=25，
∴HL=22+5AH=27AH=27m，AL=52+5AH=57AH=57m，
∵IG//AB，
∴IHAH=GHBH=210=15，
∴IH=15AH=15m，
∴LI=27m−15m=335m，
∵AD//HC，
∴△AKD∽△HKC，
∴AKHK=ADHC=55=1，
∴AK=HK=12AH=12m，
∴LK=57m−12m=314m，
∵IQ//KP，
∴△QLI∽△PLK，
∴S1S2=(LILK)2=(335m314m)2=425，
故答案为：425．
设AH分别交CD、FG、BM于点K、I、L，BM分别交CD、FG于点P、Q，设AH=m，由△HLM∽△ALB，得HLAL=HMAB=25，则HL=27m，AL=57m，由IG//AB，得IHAH=GHBH=15，则IH=15m，求得LI=335m，再证明△AKD∽△HKC，得AKHK=ADHC=1，则AK=12m，求得LK=314m，即可由△QLI∽△PLK，求得S1S2=(LILK)2=425，于是得到问题的答案．
此题重点考查正方形的性质、平行线分线段成比例定理、相似三角形的判定与性质等知识，设AH=m，求得HL=27m，AL=57m，IH=15m，AK=12m是解题的关键．
18.【答案】4013
【解析】解：过点A作AH⊥BC于点H，过点E作EG⊥CF于点G，点D与点F重合，如图，
由折叠得，AF=AD=AB=5，
∴BH=AH，
∵cs∠B=BHAB=45，
∴BH=4，
∴BF=2BH=8，
∴FC=AF−AC=8−5=3，
∵四边形ABCD是菱形，
∴CD/​/AB，
∴∠DCF=∠B，cs∠DCF=cs∠B=45=CGCE，
设CG=4y，则CE=5y，FG=CF−CG=3−4y，
由折叠得EF=DE=5−5y，
在Rt△CEG中，由勾股定理得EG= CE2−CG2=3y，
在Rt△FEG中，由勾股定理得EG2+FG2=EF2，
∴(3y)2+(3−4y)2=(5−5y)2，
解得y=813，
∴CE=5×813=4013，
故答案为：4013．
由折叠得AF=AD=AB，过点A作AH⊥BC于点H，过点E作EG⊥CF于点G，得BH=HF=4，CF=3，由菱形的性质得∠DCF=∠B，可得CGCE=45，设CG=4y，则CE=5y，由勾股定理得EG=3y，由折叠得EF=DE=5−5y，而FG=FC−CG=3−4y，在Rt△EFG中由勾股定理得(3−4y)2+(3y)2=(5−5y)2解方程求出y的值即可解决问题
本题主要考查翻折变换(折叠问题)，菱形的性质，解直角三角形，解答本题的关键是熟练掌握折叠的性质：折叠是一种对称变换，它属于轴对称，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等．
19.【答案】解：823−( 2−1)−1−| 8−3|
=(23)23−1 2−1−(3− 8)
=22− 2+1( 2−1)×( 2+1)−3+2 2
=4−( 2+1)−3+2 2
=4− 2−1−3+2 2
= 2．
【解析】先根据有理数的乘方，负整数指数幂，绝对值进行计算，再根据幂的乘方，分母有理化进行计算，再根据实数的加减法法则进行计算即可．
本题考查了分数指数幂，负整数指数幂，分母有理化，实数的混合运算等知识点，能正确根据实数的运算法则进行计算是解此题的关键．
20.【答案】解：方程两边同时乘2x(x+1)，
得3×2x=x+1+2x2+2x，
整理，得2x2−3x+1=0，
解得x=1或x=12，
检验：当x=1时，最简公分母2x(x+1)=2×1×(1+1)≠0；
当x=12时，最简公分母2x(x+1)=2×12×(12+1)≠0，
∴原方程的解是x=1或x=12．
【解析】通过方程两边都乘以最简公分母2x(x+1)，将原方程化为整式方程再求解、检验．
此题考查了分式方程的求解能力，关键是能准确理解并运用其求解方法进行变式、计算和检验．
21.【答案】解：(1)∵点C(2,m)在直线y=x+3图象上，
∴m=2+3=5，
∴C(2,5)，
∵C(2,5)在反比例函数图象上，
∴k=10，
∴反比例函数解析式为：y=10x．
(2)∵C(2,5)，点D在直线l上，CD=3，l//x轴，
∴D(5,5)或(−1,5)，
∵y=x+3与x轴、y轴分别交于点A、B，
∴A(−3,0)，B(0,3)，
①当D点坐标为(−1,5)时，
S△ABD=S梯形OEDA−S△DEB−S△AOB=12×(1+3)×5−12×1×(5−3)−12×3×3=92，
②当D点坐标为(5,5)时，
S△ABD=S△ACD−S△BCD=12×3×5−12×3×(5−3)=92．

【解析】(1)待定系数法求出反比例函数解析式即可；
(2)分两种情况求面积，①当D点坐标为(−1,5)时，②当D点坐标为(5,5)时，分别计算出△ABD的面积即可．
本题考查了反比例函数与一次函数的交点问题，熟练掌握交点坐标满足两个函数解析式是关键．
22.【答案】解：如图，过点C作CF⊥AB于点F，CG⊥BF于点G，
则四边形FBGC为矩形，
∴BF=CG，
在Rt△AFC中，AC=6米，∠ACF=17.5°，
∵tan∠ACF=AFCF，
∴AF=CF⋅tan∠ACF≈6×0.32=1.92(米)，
∴BF=AB−AF=5−1.92=3.08(米)，
在Rt△CDG中，CG=3.08米，∠CDG=36.9°，
∵tan∠CDG=CGDG，
∴DG=CGtan∠CDG≈≈4.11(米)，
在Rt△CEG中，CG=3.08米，∠CEG=82.4°，
∵tan∠CEG=CGEG，
∴EG=CGtan∠CEG≈3.087.5≈0.41(米)，
则DE=DG−EG=4.11−0.41=3.7(米)，
答：DE的长约为3.7米．
【解析】过点C作CF⊥AB于点F，CG⊥BF于点G，根据正切的定义求出AF，进而求出BF，根据正切的定义分别求出DG、EG，计算即可．
本题考查的是解直角三角形的应用−坡度坡角问题，熟记锐角三角函数的定义是解题的关键．
23.【答案】(1)证明：连接AD，
∵直径AB垂直于弦CD，垂足为点E，
∴BD=BC，
∴∠OAF=∠OAD，
∵OA=OD，
∴∠ADF=∠OAD，
∴∠OAF=∠ADF，
∵∠OFA=∠AFD，
∴△OFA∽△AFD，
∴AFDF=OFAF，
∴AF2=OF⋅DF．
(2)解：∵OA=OB=OD，CD=8，BE=2，
∴DE=CE=12CD=4，OE=OB−2=OD−2，
∵∠AED=90°，
∴OE2+DE2=OD2，
∴(OD−2)2+42=OD2，
解得OD=5，
∴OA=OB=5，OE=5−2=3，
∴AE=OA+OE=5+3=8，
∴AD= AE2+DE2= 82+42=4 5，
∵△OFA∽△AFD，
∴OFAF=OAAD=54 5，
∴AF=4 55OF，
∵AF2=OF⋅DF，
∴(4 55OF)2=OF(OF+5)，
解得OF=2511或OF=0(不符合题意，舍去)，
∴OF的长是2511．
【解析】(1)连接AD，由垂径定理得BD=BC，则∠OAF=∠OAD，由OA=OD，得∠ADF=∠OAD，所以∠OAF=∠ADF，而∠OFA=∠AFD，即可证明△OFA∽△AFD，得AFDF=OFAF，则AF2=OF⋅DF；
(2)由OA=OB=OD，CD=8，BE=2，得DE=CE=4，OE=OB−2=OD−2，由OE2+DE2=OD2，得(OD−2)2+42=OD2，求得OD=5，OE=3，所以AE=8，则AD= AE2+DE2=4 5，根据相似三角形的性质得OFAF=OAAD=54 5，则AF=4 55OF，由AF2=OF⋅DF，得(4 55OF)2=OF(OF+5)，求得OF=2511．
此题重点考查垂径定理、圆周角定理、相似三角形的判定与性质、勾股定理等知识，正确地作出辅助线是解题的关键．
24.【答案】解：(1)由抛物线的表达式知，点A(1a,4−1a)，
设直线PA的表达式为：y=kx+4，
将点A的坐标代入上式得：4−1a=k×1a+4，
解得：k=−1，
即直线PA的表达式为：y=−x+4；
(2)由旋转的性质得，点Q(1a−4,1a)，
将点Q的坐标代入抛物线表达式得：1a=a(1a−4)2−2(1a−4)+4，
解得：a=14(舍去)或−12，
则抛物线的表达式为：y=−12x2−2x+4；
(3)由直线PA的表达式知，其和x轴负半轴的夹角为45°，点A(−2,6)，
设将(2)中得到的抛物线沿射线PA平移 2m个单位，则相当于向左、向上个平移了m个单位，
则平移后的抛物线表达式为：y=−12(x−m)2−2(x−m)+4+m，
当x=0时，y=−12(x−m)2−2(x−m)+4+m=−12m2−m+4，即点C的坐标为：(0,−12m2−m+4)，
则PC=12m2+m+4，
而 2AB= 2× 2m=2m=PC=12m2+m+4，
解得：m=2，
则点C(0,0)，即点C、O重合，
由点A的坐标(−2,6)得到点B(−4,8)，
在△PBC中，CP=4，BC= 80，PB=4 2，
过点P作PH⊥BC于点H，

则S△PBC=12×PC×|xB|=12BC×PH，
即4×4= 80×PH，则PH=16 80，
则sin∠PBC=PHPB=16 804 2=1 10，
则tan∠PBC=13．
【解析】(1)由待定系数法即可求解；
(2)由旋转的性质得，点Q(1a−4,1a)，将点Q的坐标代入抛物线表达式，即可求解；
(3)求出点C的坐标为：(0,−12m2−m+4)，由PC= 2AB，求出m=2，进而求解．
主要考查了二次函数的解析式的求法和与几何图形结合的综合能力的培养．要会利用数形结合的思想把代数和几何图形结合起来，利用点的坐标的意义表示线段的长度，从而求出线段之间的关系，解决相关问题．
25.【答案】(1)证明：①如图1，设AC与DE的交点为M，
由折叠可EM=MO，
∵E、D点关于AC对称，
∴EO⊥AC，
∵EO是圆O的半径，
∴AM=CM，
∴AC、EO互相垂直平分，
∴四边形ADCE是菱形；
②解：∵四边形ADCE是菱形，
∴∠EAC=∠CAO=∠ECA=∠ACO，
∵AM⊥MO，MO=12AO，
∴∠MAO=30°，
∴∠AOM=∠MOC=60°，
∵DO=BO，
∴∠OEB=∠OBE=30°，
∴∠EGO=90°，
∵∠FCG=30°，
∴CF=2FG，
∵∠CEF=∠ECF=30°，
∴EF=FC=2FG，
∵EG=GB，
∴EB=6FG，
∴FGBE=16；
(2)解：如图2，当D点在O点左侧时，过O点作OM⊥AC交于M点，过点O作OH⊥AE交于H点，过点E作EN⊥AB交于N点，
由对称可知，AE=AD，
∵AO=5，OD=1，
∴AE=AD=4，
∵ED//MO，
∴GDMO=45，
设GD=4m，则MO=5m，
∵E、D点关于AC对称，
∴EG=4m，
∴ED=8m，
∵AH=HE=2，
∴cs∠EAD=25，
∴AN=4×25=85，
∴ND=4−85=125，EN=4 215，
∴ED=8m=4 305，
∴m= 3010，
∴MO= 302，
∴AM= 702，
∴AC= 70；
如图3，当D点在O点右侧时，同理可求AC=4 5；
综上所述：AC的长为4 5或 70．
【解析】(1)①设AC与DE的交点为M，通过推导出AC、EO互相垂直平分，证明四边形ADCE是菱形；
②先求出菱形ADCE的内角为60°，再推导出CF=2FG，即可推导出EB=6FG，可得FGBE=16；
(2)当D点在O点左侧时，过O点作OM⊥AC交于M点，过点O作OH⊥AE交于H点，过点E作EN⊥AB交于N点，设GD=4m，则MO=5m，EG=4m，ED=8m，先求出cs∠EAD=25，即可分别求出AN=4×25=85，ND=4−85=125，EN=4 215，ED=8m=4 305，得到m= 3010，则MO= 302，AM= 702，再求AC= 70；当D点在O点右侧时，同理可求AC=4 5．
本题考查圆的综合应用，熟练掌握折叠的性质，垂径定理，直角三角形的性质是解题的关键．