【二轮复习】高考数学 专题1.1 集合与常用逻辑用语（题型专练）（新高考专用）.zip

这是一份【二轮复习】高考数学 专题1.1 集合与常用逻辑用语（题型专练）（新高考专用）.zip，文件包含二轮复习高考数学专题11集合与常用逻辑用语题型专练新高考专用原卷版docx、二轮复习高考数学专题11集合与常用逻辑用语题型专练新高考专用解析版docx等2份试卷配套教学资源，其中试卷共24页， 欢迎下载使用。

TOC \ "1-3" \h \u
\l "_Tc18314" 【题型1 集合中元素个数问题】 PAGEREF _Tc18314 \h 3
\l "_Tc25854" 【题型2 子集的个数问题】 PAGEREF _Tc25854 \h 5
\l "_Tc8123" 【题型3 集合的交、并、补集运算】 PAGEREF _Tc8123 \h 6
\l "_Tc5734" 【题型4 集合中的含参问题】 PAGEREF _Tc5734 \h 7
\l "_Tc23857" 【题型5 集合的新定义问题】 PAGEREF _Tc23857 \h 8
\l "_Tc27161" 【题型6 充分条件与必要条件】 PAGEREF _Tc27161 \h 9
\l "_Tc14964" 【题型7 全称量词与存在量词命题】 PAGEREF _Tc14964 \h 11
1、集合
集合是高考数学的必考考点，常见以一元一次、一元二次不等式的形式，结合有限集、无限集来考查集合的交、并、补集等运算，偶尔涉及集合的符号辨识，一般出现在高考的第1题，以简单题为主。
2、常用逻辑用语
常用逻辑用语是高考数学的重要考点，常见于考查真假命题的判断；全称量词命题、存在量词命题以及命题的否定；偶尔涉及充分条件与必要条件以及根据描述进行逻辑推理等，中等偏易难度。但一般很少单独考查，常常与函数、不等式、数列、三角函数、立体几何等知识交汇，热点是“充要条件”,考生复习时需多注意加强这方面练习。
【知识点1 集合】
1．集合与元素
(1)集合中元素的三个特征：确定性、互异性、无序性．
(2)元素与集合的关系是属于或不属于，用符号∈或∉表示．
(3)集合的表示法：列举法、描述法、图示法．
(4)常见数集的记法
2．集合的基本关系
(1)子集：若对于任意的x∈A都有x∈B，则A⊆B；
(2)真子集：若A⊆B，且A≠B，则A⫋B；
(3)相等：若A⊆B，且B⊆A，则A＝B；
(4)∅是任何集合的子集，是任何非空集合的真子集．
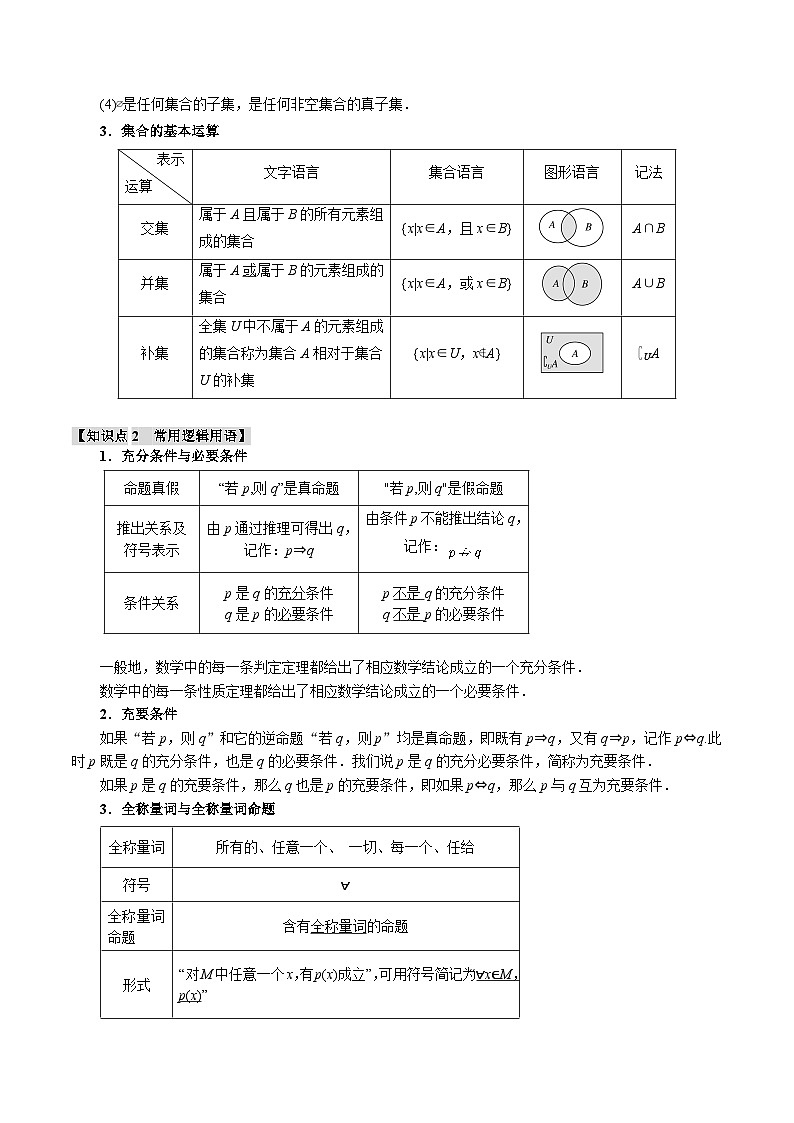
3．集合的基本运算
【知识点2 常用逻辑用语】
1．充分条件与必要条件
一般地，数学中的每一条判定定理都给出了相应数学结论成立的一个充分条件．
数学中的每一条性质定理都给出了相应数学结论成立的一个必要条件．
2．充要条件
如果“若p，则q”和它的逆命题“若q，则p”均是真命题，即既有p⇒q，又有q⇒p，记作p⇔q.此时p既是q的充分条件，也是q的必要条件．我们说p是q的充分必要条件，简称为充要条件．
如果p是q的充要条件，那么q也是p的充要条件，即如果p⇔q，那么p与q互为充要条件．
3．全称量词与全称量词命题
4.存在量词与存在量词命题
5．全称量词命题与存在量词命题的否定
(1)全称量词命题p：∀x∈M，p(x)的否定：∃x∈M，¬p(x)；全称量词命题的否定是存在量词命题．
(2)存在量词命题p：∃x∈M，p(x)的否定：∀x∈M，¬p(x)；存在量词命题的否定是全称量词命题．
【题型1 集合中元素个数问题】
【例1】（2023·河南郑州·统考模拟预测）已知集合P=nn=2k−1,k∈N∗,k≤10，Q=2,3,5，则集合T=xyx∈P,y∈Q中元素的个数为（ ）
A．30B．28C．26D．24
【解题思路】根据题意得到P=1,3,5,7,9,11,13,15,17,19，再结合T=xyx∈P,y∈Q求解即可.
【解答过程】P=nn=2k−1,k∈N∗,k≤10=1,3,5,7,9,11,13,15,17,19，Q=2,3,5，
因为T=xyx∈P,y∈Q，
当x∈P,y=2时，xy为偶数，共有10个元素.
当x∈P,y=3时，xy为奇数，
此时xy=3,9,15,21,27,33,39,45,51,57，共有10个元素.
当x∈P,y=5时，xy为奇数，
此时xy=5,15,25,35,45,55,65,75,85,95，有重复数字15,45，去掉，共有8个元素.
综上T=xyx∈P,y∈Q中元素的个数为10+10+8=28个.
故选：B.
【变式1-1】（2023上·辽宁大连·高一校考阶段练习）已知A是由0，m，m2−3m+2三个元素组成的集合，且2∈A，则实数m为（ ）
A．2B．3C．0或3D．0，2，3均可
【解题思路】由2∈A，可得m=2或m2−3m+2=2，解方程求m，再去验证是否符合集合中元素性质即可．
【解答过程】因为集合A是由0，m，m2−3m+2三个元素组成的集合，
所以A=0,m,m2−3m+2，又2∈A，
所以m=2或m2−3m+2=2，解方程可得m=2或m=0或m=3，
当m=2时，A=0,2，与已知矛盾，舍去；
当m=0时，A=0,2，与已知矛盾，舍去；
当m=3时，A=0,3,2，满足题意，∴m=3，B正确，
故选：B.
【变式1-2】（2022上·河南商丘·高一校考阶段练习）已知集合A=xax2-3x+2=0的元素只有一个，则实数a的值为（ ）
A．98B．0C．98或0D．无解
【解题思路】集合A有一个元素，即方程ax2-3x+2=0有一解，分a=0，a≠0 两种情况讨论，即可得解.
【解答过程】集合A有一个元素，即方程ax2-3x+2=0有一解，
当a=0时，A=xax2-3x+2=0=x-3x+2=0=23，符合题意，
当a≠0时，ax2-3x+2=0有一解，
则Δ=9-8a=0，解得：a=98，
综上可得：a=0或a=98，
故选：C.
【变式1-3】（2023·河北·河北衡水中学校考模拟预测）若集合U有71个元素，S,T⊆U且各有14，28个元素，则∁S∪TS∩T的元素个数最少是（ ）
A．14B．30C．32D．42
【解题思路】根据集合中的元素以及交并补运算的性质即可求解.
【解答过程】设S∩T=M,M中有x个元素，则0≤x≤14,x∈N,
所以S∪T中的元素个数为14+28−x=42−x，因此∁S∪TS∩T中的元素个数为S∪T中的元素减去S∩T中的元素个数，即为42−x−x=42−2x，
由于0≤x≤14,x∈N，所以42−2x∈14,42，故当x=14时，有最小值14
故选：A.
【题型2 子集的个数问题】
【例2】（2023·河南·校联考二模）集合A=x1