







【三轮冲刺】2024年高考数学新结构模拟卷(一).zip
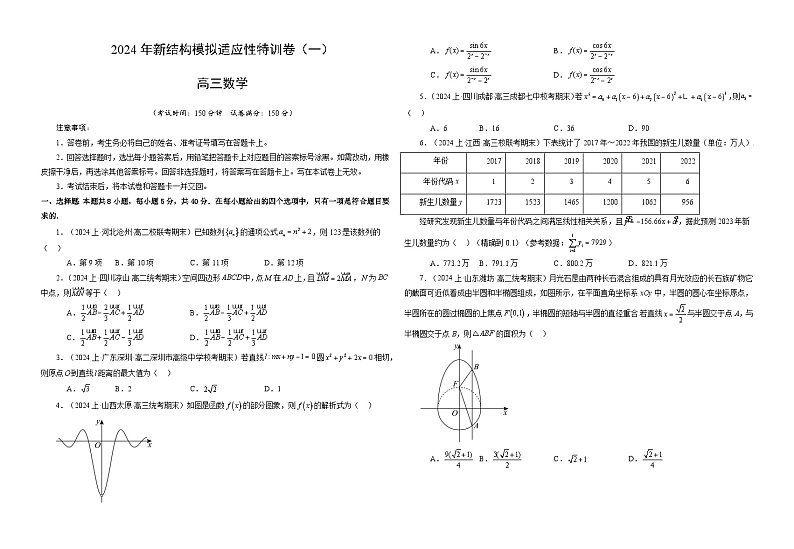
展开一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
三、填空题:本题共3小题,每小题5分,共15分.
12
13 /
14
四、解答题:本题共5小题,其中第15题13分,第16,17题15分,第18,19题17分,共77分.解答应写出文字说明、证明过程或演算步骤.
15.(满分13分)
【答案】(1)
(2)
【分析】(1)由正弦定理和三角恒等变换得到,求出角;
(2)由余弦定理和面积公式得到方程,求出,进而求出周长.
【详解】(1)由,得
由正弦定理,得.
.
.
又,
.
又,
.
又,
.
(2)由(1)知,
①
又,故,
,②
又,
由①②,得,故,
∴,
故,周长为.
16.(满分15分)
【答案】(1)
(2)点为的中点
【分析】(1)由题设条件建系,表示出相关点,分别计算坐标和平面的法向量坐标,利用线面所成角的空间向量计算公式即得;
(2)在原有坐标系中,设出参数表示出点的坐标,分别计算平面与平面的法向量,利用面面所成角的空间向量计算公式列出方程解之即得.
【详解】(1)
如图,分别以为轴的正方向建立空间直角坐标系.则
于是,,设平面的法向量为,
则
故可取.设直线与平面所成角为,
则
即直线与平面所成角的正弦值是.
(2)
如图,设,,则,因,故,解得:,
则,设平面的法向量为,
则故可取.
又,设平面的法向量为,
则故可取.
设平面与平面的夹角为,则,
解得:或,因,故,即当点为的中点时,平面与平面的夹角的余弦值为.
17.(满分15分)
【答案】(1)
(2)
【分析】(1)根据题中条件列出方程组,解出即可;
(2)错位相减后得到结果,再用错位相减法进行计算,即可求解.
【详解】(1)设,
由题意得,即,解得或(舍去)
.
(2)由(1)可得,
则,①
可得:,②
①-②可得:,
设.③
,④
③-④可得:
,
则,
,
.
18.(满分17分)
【答案】(1)
(2)证明见解析
【分析】(1)分类讨论,利用导数判断函数的单调区间,根据极大值建立方程求解即可;
(2)把问题转化为证明,构造函数,利用导数研究函数最值即可证明.
【详解】(1)的定义域为,.
当时,,在上单调递增,函数无极值;
当时,令,得,令,得,
所以在上单调递增,在上单调递减,
故当时,取得极大值,极大值为,解得.
经验证符合题意,故实数a的值为.
(2)当时,,故要证,即证.
令,则,.
令,,则,
所以在上单调递增,
又因为,,
所以,使得,即,
当时,,当时,,
所以在上单调递减,在上单调递增,
所以.
又因为,即,
所以,
所以,即,故得证.
19.(满分17分)
【答案】(1)证明见解析
(2)不可信
【分析】(1)利用马尔科夫不等式的证明示例证明即可;
(2)由题意可知治愈的人数为服从二项分布,由二项分布计算均值与方差,再结合切比雪夫不等式说明即可.
【详解】(1)法一:对非负离散型随机变量及正数使用马尔科夫不等式,
有.
法二:设的分布列为
其中,记,则对任意,
.(2)设在100名患者中治愈的人数为.假设药企关于此新药有效率的宣传内容是客观真实的,
那么在此假设下,.
由切比雪夫不等式,有.
即在假设下,100名患者中治愈人数不超过60人的概率不超过0.04,此概率很小,
据此我们有理由推断药厂的宣传内容不可信.
序号
1
2
3
4
5
6
7
8
答案
C
C
B
C
C
A
D
D
序号
9
10
11
答案
BC
ABD
ABD
【三轮冲刺】高考数学 押题预测卷03(新高考九省联考题型).zip: 这是一份【三轮冲刺】高考数学 押题预测卷03(新高考九省联考题型).zip,文件包含三轮冲刺高考数学押题预测卷03新高考九省联考题型原卷版docx、三轮冲刺高考数学押题预测卷03新高考九省联考题型解析版docx等2份试卷配套教学资源,其中试卷共21页, 欢迎下载使用。
【三轮冲刺】高考数学 押题预测卷02(新高考九省联考题型).zip: 这是一份【三轮冲刺】高考数学 押题预测卷02(新高考九省联考题型).zip,文件包含三轮冲刺高考数学押题预测卷02新高考九省联考题型原卷版docx、三轮冲刺高考数学押题预测卷02新高考九省联考题型解析版docx等2份试卷配套教学资源,其中试卷共20页, 欢迎下载使用。
【三轮冲刺】高考数学 押题预测卷01(新高考九省联考题型).zip: 这是一份【三轮冲刺】高考数学 押题预测卷01(新高考九省联考题型).zip,文件包含三轮冲刺高考数学押题预测卷01新高考九省联考题型原卷版docx、三轮冲刺高考数学押题预测卷01新高考九省联考题型解析版docx等2份试卷配套教学资源,其中试卷共23页, 欢迎下载使用。












