培优冲刺01三角形中的常见模型综合训练（14模型）2024年中考数学复习冲刺过关（全国通用）

这是一份培优冲刺01三角形中的常见模型综合训练（14模型）2024年中考数学复习冲刺过关（全国通用），文件包含培优专题01三角形中的常见模型综合训练原卷版docx、培优专题01三角形中的常见模型综合训练解析版docx等2份试卷配套教学资源，其中试卷共97页， 欢迎下载使用。

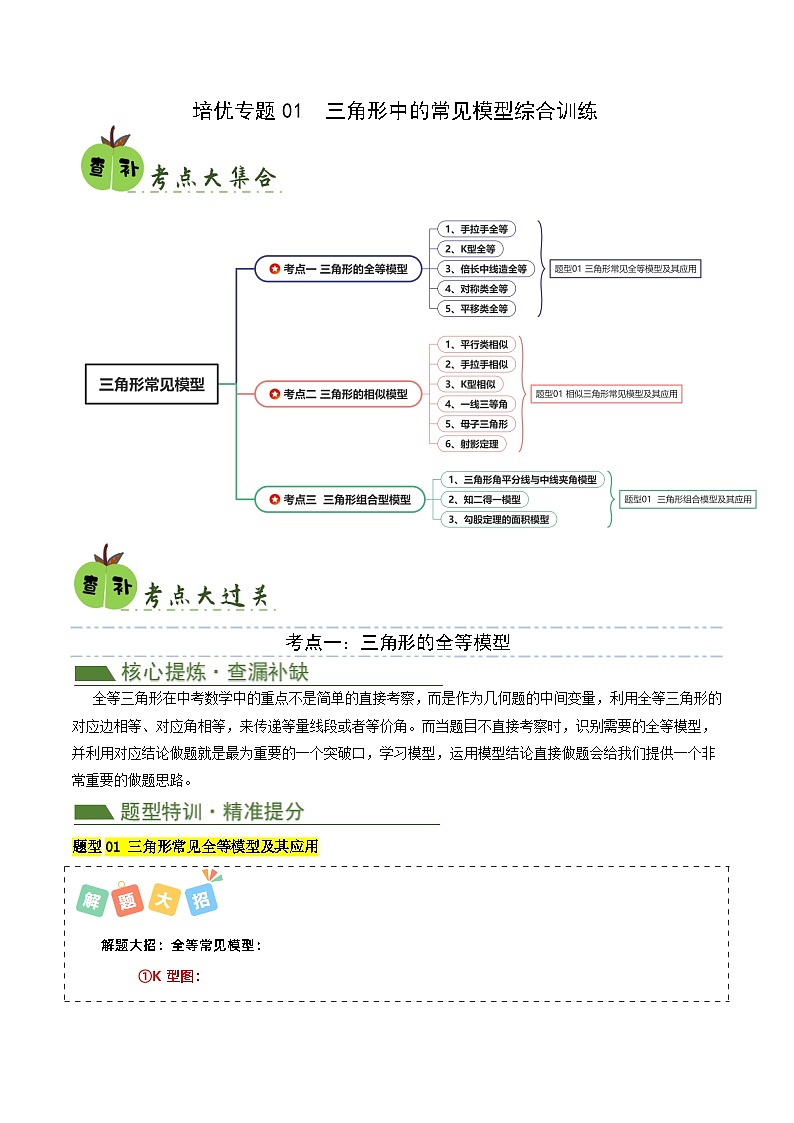
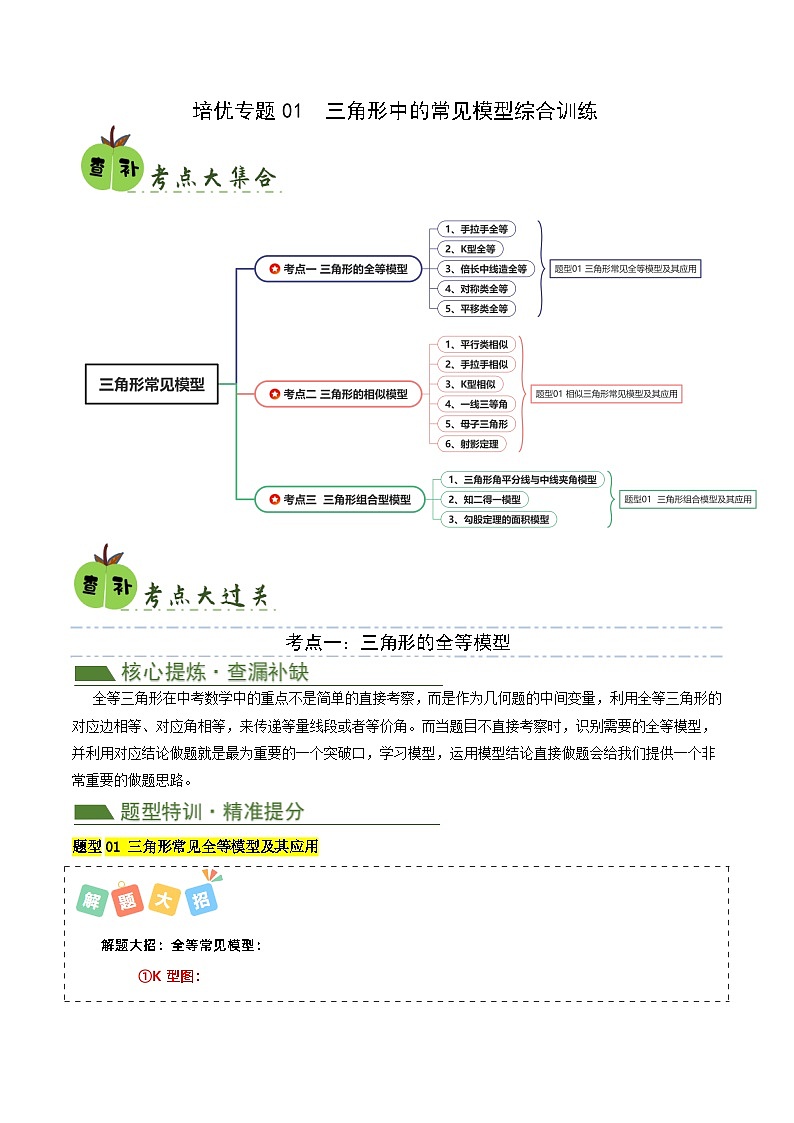
考点一：三角形的全等模型
全等三角形在中考数学中的重点不是简单的直接考察，而是作为几何题的中间变量，利用全等三角形的对应边相等、对应角相等，来传递等量线段或者等价角。而当题目不直接考察时，识别需要的全等模型，并利用对应结论做题就是最为重要的一个突破口，学习模型，运用模型结论直接做题会给我们提供一个非常重要的做题思路。
题型01 三角形常见全等模型及其应用
【中考真题练】
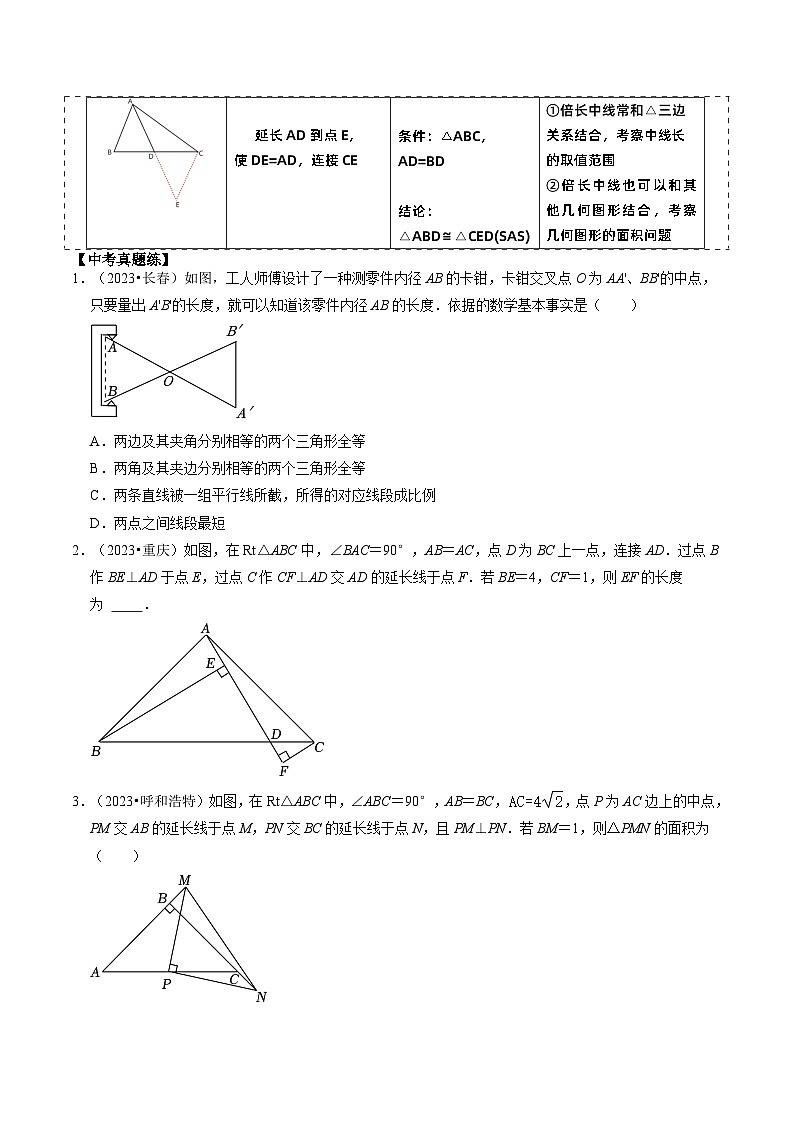
1．（2023•长春）如图，工人师傅设计了一种测零件内径AB的卡钳，卡钳交叉点O为AA'、BB'的中点，只要量出A'B'的长度，就可以知道该零件内径AB的长度．依据的数学基本事实是（ ）
A．两边及其夹角分别相等的两个三角形全等
B．两角及其夹边分别相等的两个三角形全等
C．两条直线被一组平行线所截，所得的对应线段成比例
D．两点之间线段最短
2．（2023•重庆）如图，在Rt△ABC中，∠BAC＝90°，AB＝AC，点D为BC上一点，连接AD．过点B作BE⊥AD于点E，过点C作CF⊥AD交AD的延长线于点F．若BE＝4，CF＝1，则EF的长度为 ．
3．（2023•呼和浩特）如图，在Rt△ABC中，∠ABC＝90°，AB＝BC，，点P为AC边上的中点，PM交AB的延长线于点M，PN交BC的延长线于点N，且PM⊥PN．若BM＝1，则△PMN的面积为（ ）
A．13B．C．8D．

4．（2023•湖北）如图，△BAC，△DEB和△AEF都是等腰直角三角形，∠BAC＝∠DEB＝∠AEF＝90°，点E在△ABC内，BE＞AE，连接DF交AE于点G，DE交AB于点H，连接CF．给出下面四个结论：①∠DBA＝∠EBC；②∠BHE＝∠EGF；③AB＝DF；④AD＝CF．其中所有正确结论的序号是 ．

5．（2023•遂宁）如图，以△ABC的边AB、AC为腰分别向外作等腰直角△ABE、△ACD，连结ED、BD、EC，过点A的直线l分别交线段DE、BC于点M、N．以下说法：①当AB＝AC＝BC时，∠AED＝30°；②EC＝BD；③若AB＝3，AC＝4，BC＝6，则DE＝2；④当直线l⊥BC时，点M为线段DE的中点．正确的有 ．（填序号）

6．（2023•鞍山）如图，在正方形ABCD中，点M为CD边上一点，连接AM，将△ADM绕点A顺时针旋转90°得到△ABN，在AM，AN上分别截取AE，AF，使AE＝AF＝BC，连接EF，交对角线BD于点G，连接AG并延长交BC于点H．若AM＝，CH＝2，则AG的长为 ．

7．（2023•大连）如图，AC＝AE，BC＝DE，BC的延长线与DE相交于点F，∠ACF+∠AED＝180°．求证：AB＝AD．

8．（2023•遂宁）如图，四边形ABCD中，AD∥BC，点O为对角线BD的中点，过点O的直线l分别与AD、BC所在的直线相交于点E、F．（点E不与点D重合）
（1）求证：△DOE≌△BOF；
（2）当直线l⊥BD时，连结BE、DF，试判断四边形EBFD的形状，并说明理由．

9．（2023•巴中）综合与实践．
（1）提出问题．如图1，在△ABC和△ADE中，∠BAC＝∠DAE＝90°，且AB＝AC，AD＝AE，连接BD，连接CE交BD的延长线于点O．
①∠BOC的度数是 ．
②BD：CE＝ ．
（2）类比探究．如图2，在△ABC和△DEC中，∠BAC＝∠EDC＝90°，且AB＝AC，DE＝DC，连接AD、BE并延长交于点O．
①∠AOB的度数是 ；
②AD：BE＝ ．
（3）问题解决．如图3，在等边△ABC中，AD⊥BC于点D，点E在线段AD上（不与A重合），以AE为边在AD的左侧构造等边△AEF，将△AEF绕着点A在平面内顺时针旋转任意角度．如图4，M为EF的中点，N为BE的中点．
①说明△MND为等腰三角形．
②求∠MND的度数．

【中考模拟练】
1．（2023•三穗县校级一模）如图，点D，E分别为△ABC的边AB，AC上的点，连接DE并延长至F，使EF＝DE，连接FC．若FC∥AB，AB＝5，CF＝3，则BD的长等于（ ）
A．1B．2C．3D．5

2．（2024•昆山市一模）如图，在平行四边形ABCD中，AD＝5，AB＝6，∠D是锐角，CE⊥AD于点E，F是CD的中点，连接BF，EF．若∠EFB＝90°，则CE的长为 ．

3．（2023•福田区二模）如图，正方形ABCD的边长为8，对角线AC，BD相交于点O，点M，N分别在边BC，CD上，且∠MON＝90°，连接MN交OC于P，若BM＝2，则OP•OC＝ ．

4．（2024•河南一模）如图，在菱形OABC中，∠BCO＝60°，点C（﹣3，0），点D在对角线BO上，且OD＝2BD，点E是射线AO上一动点，连接DE，F为x轴上一点（F在DE左侧），且∠EDF＝60°，连接EF，当△DEF的周长最小时，点E的坐标为（ ）
A．（1，3）B．C．D．（0，0）

5．（2023•长春模拟）两个大小不同的等边三角形三角板按图①所示摆放．将两个三角板抽象成如图②所示的△ABC和△ADE，点B、C、D依次在同一条直线上，连接CE．若CD＝1，CE＝3，则点A到直线BC的距离为 ．

6．（2024•雁塔区校级二模）已知：如图，点E、F在BC上，AF与DE交于点G，AB＝DC，GE＝GF，∠B＝∠C．求证：AG＝DG．

7．（2024•凉州区一模）某同学用10块高度都是5cm的相同长方体小木块，垒了两堵与地面垂直的木墙，木墙之间刚好可以放进一个等腰直角三角板ABD（∠ABD＝90°，BD＝BA），点B在CE上，点A和D分别与木墙的顶端重合．
（1）求证：△ACB≌△BED；
（2）求两堵木墙之间的距离．

8．（2024•龙马潭区一模）如图，抛物线y＝ax2+bx+6（a≠0）与x轴交于A（﹣1，0），B（3，0）两点，与y轴交于点C，顶点为D．
（1）求抛物线的解析式；
（2）若在线段BC上存在一点M，使得∠BMO＝45°，过点O作OH⊥OM交BC的延长线于点H，求点M的坐标；
（3）点P是y轴上一动点，点Q是在对称轴上一动点，是否存在点P，Q，使得以点P，Q，C，D为顶点的四边形是菱形？若存在，求出点Q的坐标；若不存在，请说明理由．

考点二：三角形的相似模型
相似三角形和勾股定理是解决初中数学求长度问题中的两大重要定理，所有的几何问题就长度，最后几乎都能转化为这两个定理的应用。而作为应用几率更大的相似三角形，熟悉其常用模型，利用模型的性质思考对应问题的走向就是一个非常重要的解题思想。所以，先熟悉相似的各种模型，再在问题中识别模型，最后利用模型找捷径。
题型01 相似三角形常见模型及其应用
【中考真题练】
1．（2023•哈尔滨）如图，AC，BD相交于点O，AB∥DC，M是AB的中点，MN∥AC，交BD于点N，若DO：OB＝1：2，AC＝12，则MN的长为（ ）
A．2B．4C．6D．8

2．（2023•东营）如图，△ABC为等边三角形，点D，E分别在边BC，AB上，∠ADE＝60°．若BD＝4DC，DE＝2.4，则AD的长为（ ）
A．1.8B．2.4C．3D．3.2

3．（2023•雅安）如图，在▱ABCD中，F是AD上一点，CF交BD于点E，CF的延长线交BA的延长线于点G，EF＝1，EC＝3，则GF的长为（ ）
A．4B．6C．8D．10

4．（2023•德州）如图，A，B，C，D是⊙O上的点，AB＝AD，AC与BD交于点E，AE＝3，EC＝5，BD＝4，⊙O的半径为（ ）
A．6B．C．5D．2

5．（2023•东营）如图，正方形ABCD的边长为4，点E，F分别在边DC，BC上，且BF＝CE，AE平分∠CAD，连接DF，分别交AE，AC于点G，M．P是线段AG上的一个动点，过点P作PN⊥AC，垂足为N，连接PM．有下列四个结论：
①AE垂直平分DM；
②PM+PN的最小值为3；
③CF2＝GE•AE；
④S△ADM＝6．
其中正确的是（ ）
A．①②B．②③④C．①③④D．①③

6．（2023•大庆）在综合与实践课上，老师组织同学们以“矩形的折叠”为主题开展数学活动．有一张矩形纸片ABCD如图所示，点N在边AD上，现将矩形折叠，折痕为BN，点A对应的点记为点M，若点M恰好落在边DC上，则图中与△NDM一定相似的三角形是 ．

7．（2023•呼和浩特）如图，正方形ABCD的边长为，点E是CD的中点，BE与AC交于点M，F是AD上一点，连接BF分别交AC，AE于点G，H，且BF⊥AE，连接MH，则AH＝ ，MH＝ ．

8．（2023•常德）如图1，在Rt△ABC中，∠ABC＝90°，AB＝8，BC＝6，D是AB上一点，且AD＝2，过点D作DE∥BC交AC于E，将△ADE绕A点顺时针旋转到图2的位置．则图2中的值为 ．

9．（2023•鄂州）2002年的国际数学家大会在中国北京举行，这是21世纪全世界数学家的第一次大聚会．这次大会的会徽选定了我国古代数学家赵爽用来证明勾股定理的弦图，世人称之为“赵爽弦图”．如图，用四个全等的直角三角形（Rt△AHB≌Rt△BEC≌Rt△CFD≌Rt△DGA）拼成“赵爽弦图”，得到正方形ABCD与正方形EFGH，连接AC和EG，AC与DF、EG、BH分别相交于点P、O、Q，若BE：EQ＝3：2，则的值是 ．

10．（2023•湘潭）在Rt△ABC中，∠BAC＝90°，AD是斜边BC上的高．
（1）证明：△ABD∽△CBA；
（2）若AB＝6，BC＝10，求BD的长．

11．（2023•南京）在平面内，将一个多边形先绕自身的顶点A旋转一个角度θ（0°＜θ＜180°），再将旋转后的多边形以点A为位似中心放大或缩小，使所得多边形与原多边形对应线段的比为k，称这种变换为自旋转位似变换．若顺时针旋转，记作T（A，顺θ，k）；若逆时针旋转，记作T（A，逆θ，k）．
例如：如图①，先将△ABC绕点B逆时针旋转50°，得到△A1BC1，再将△A1BC1以点B为位似中心缩小到原来的，得到△A2BC2，这个变换记作T（B，逆50°，）．
（1）如图②，△ABC经过T（C，顺60°，2）得到△A′B′C，用尺规作出△A′B′C．（保留作图痕迹）
（2）如图③，△ABC经过T（B，逆α，k1）得到△EBD，△ABC经过T（C，顺β，k2）得到△FDC，连接AE，AF．求证：四边形AFDE是平行四边形．
（3）如图④，在△ABC中，∠A＝150°，AB＝2，AC＝1．若△ABC经过（2）中的变换得到的四边形AFDE是正方形．
Ⅰ．用尺规作出点D（保留作图痕迹，写出必要的文字说明）；
Ⅱ．直接写出AE的长．

【中考模拟练】
1．（2024•沙坪坝区模拟）如图，在平面直角坐标系中，△OAB和△OCD是以原点O为位似中心的位似图形．若OB＝2OD，△OCD的周长为3，则△OAB的周长为（ ）
A．6B．9C．12D．30

2．（2024•平遥县一模）如图，D，E分别是△ABC的边AB，AC的点，且，CD与BE交于点O，则S△COE：S△BOC的值为（ ）
A．B．C．D．

3．（2024•镇海区校级模拟）如图，△ABC和△CDE都是等边三角形，点G在CA的延长线上，GB＝GE，若BE+CG＝10，＝，则AF的长为（ ）
A．1B．C．D．2

4．（2024•龙湖区校级一模）边长为4的正方形ABCD中，对角线AC，BD交于点O，E在BD上，作EF⊥CE交AB于点F，连接CF交BD于H，则下列结论：①EF＝EC；②CF2＝CG•CA；③BE•DH＝16；④若BF＝1，则，正确的是（ ）
A．①②④B．②③④C．①②③D．①②③④

5．（2024•河北模拟）如图，△ABC中，AB＝AC＝4，BC＝2，以AB为直径的⊙O分别交AC，BC于点D，E，连接ED，则CD的长为（ ）
A．1B．C．2D．

6．（2024•宁波模拟）如图，在正方形ABCD中，G为BC上一点，矩形DEFG的边EF经过点A．若∠CDG＝α，则∠AHF＝ ；若AH＝3，GC＝2，则△EFH的面积为 ．

7．（2024•沈阳模拟）如图，矩形ABCD中，AB＝4，AD＝5，E是AB边上一点，且AE＝1，F是AD边上一动点，作∠EFG＝90°，交CD边于点G，将△FDG沿着FG所在直线折叠，点D的对应点D′恰好落在BC边上，则DF的长为 ．

8．（2024•伊宁市校级一模）如图，在正方形ABCD中，对角线AC，BD交于点O，点E在AC上，EF⊥BE交CD于点F，且F为CD的中点，交BD于点G，连接BF交AC于点H，连接GH．下列结论：①∠EFB＝45°；②；③EH＝2GH；④GO•BG＝GH•GD．其中正确结论的序号为 ．

9．（2023•新抚区模拟）如图，在△ABC中，∠ACB＝90°，AC＝2，BC＝4，AE＝3，连接BE，以BE为斜边在BE的右侧作等腰直角△BDE，P是AE边上的一点，连接PC和CD，当∠PCD＝45°，则PE长为 ．

10．（2024•汝南县一模）某“综合与实践”小组开展测量本校旗杆高度的实践活动．他们制订了测量方案，并利用课余时间完成了实地测量，测量报告如下．
请根据以上测量结果及该小组的思路．求学校旗杆AB的高度．

11．（2024•中山市一模）【感知】如图①，在正方形ABCD中，E为AB边上一点，连结DE，过点E作EF⊥DE交BC于点F．易证：△AED∽△BFE．（不需要证明）
【探究】如图②，在矩形ABCD中，E为AB边上一点，连结DE，过点E作EF⊥DE交BC于点F．
（1）求证：△AED∽△BFE．
（2）若AB＝10，AD＝6，E为AB的中点，求BF的长．
【应用】如图③，在△ABC中，∠ACB＝90°，AC＝BC，AB＝4．E为AB边上一点（点E不与点A、B重合），连结CE，过点E作∠CEF＝45°交BC于点F．当△CEF为等腰三角形时，BE的长为 ．

考点三：三角形的组合模型
三角形除了全等模型，还有一些可以得到特殊性质或者结论的组合模型，即当两个或者三个条件同时出现，就会有一些固定用法，这类模型我们叫它组合模型。
题型01 三角形组合模型及其应用
【中考真题练】
1．（2023•衢州）如图，在△ABC中，以点A为圆心，适当长为半径画弧，分别交AB，AC于点D，E．分别以点D，E为圆心，大于长为半径画弧，交于∠BAC内一点F．连结AF并延长，交BC于点G．连结DG，EG．添加下列条件，不能使BG＝CG成立的是（ ）
A．AB＝ACB．AG⊥BCC．∠DGB＝∠EGCD．AG＝AC

2．（2023•扬州）我国汉代数学家赵爽证明勾股定理时创制了一幅“勾股圆方图”，后人称之为“赵爽弦图”，它是由4个全等的直角三角形和一个小正方形组成．如图，直角三角形的直角边长为a、b，斜边长为c，若b﹣a＝4，c＝20，则每个直角三角形的面积为 ．

3．（2023•潍坊）如图，在△ABC中，CD平分∠ACB，AE⊥CD，垂足为点E，过点E作EF∥BC，交AC于点F，G为BC的中点，连接FG．求证：FG＝AB．

4．（2023•黄石）如图，AB为⊙O的直径，DA和⊙O相交于点F，AC平分∠DAB，点C在⊙O上，且CD⊥DA，AC交BF于点P．
（1）求证：CD是⊙O的切线；
（2）求证：AC•PC＝BC2；
（3）已知BC2＝3FP•DC，求的值．

5．（2023•怀化）如图，AB是⊙O的直径，点P是⊙O外一点，PA与⊙O相切于点A，点C为⊙O上的一点．连接PC、AC、OC，且PC＝PA．
（1）求证：PC为⊙O的切线；
（2）延长PC与AB的延长线交于点D，求证：PD•OC＝PA•OD；
（3）若∠CAB＝30°，OD＝8，求阴影部分的面积．

【中考模拟练】
1．（2023•武安市三模）有一题目：“如图，∠ABC＝40°，BD平分∠ABC，过点D作DE∥AB交BC于点E，若点F在AB上，且满足DF＝DE，求∠DFB的度数．”小贤的解答：以D为圆心，DE长为半径画圆交AB于点F，连接DF，则DE＝DF，由图形的对称性可得∠DFB＝∠DEB．结合平行线的性质可求得∠DFB＝140°．而小军说：“小贤考虑的不周全，∠DFB还应有另一个不同的值”．下列判断正确的是（ ）
A．小军说的对，且∠DFB的另一个值是40°
B．小军说的不对，∠DFB只有140°一个值
C．小贤求的结果不对，∠DFB应该是20°
D．两人都不对，∠DFB应有3个不同值

2．（2024•碑林区校级自主招生）图1是我国古代著名的“赵爽弦图”的示意图，它是由四个全等的直角三角形围成的．若AC＝6，BC＝5，将四个直角三角形中边长为6的直角边分别向外延长一倍，得到图2所示的“数学风车”，则这个风车的外围周长是多少？

3．（2022•长春二模）图1中的直角三角形有一条直角边长为3，将四个图1中的直角三角形分别拼成如图2，图3所示的正方形，其中阴影部分的面积分别记为S1，S2，则S1﹣S2的值为 ．

4．（2023•长春模拟）两个大小不同的等边三角形三角板按图①所示摆放．将两个三角板抽象成如图②所示的△ABC和△ADE，点B、C、D依次在同一条直线上，连接CE．若CD＝1，CE＝3，则点A到直线BC的距离为 ．

5．（2024•朝阳区一模）【教材呈现】下面是华师版八年级上册数学教材第96页的部分内容．
我们已经知道角是轴对称图形，角平分线所在的直线是角的对称轴．如图，OC是∠AOB的平分线，P是OC上任一点，作PD⊥OA，PE⊥OB，垂足分别为点D和点E．将∠AOB沿OC对折，我们发现PD与PE完全重合．由此即有：
角平分线的性质定理角平分线上的点到角两边的距离相等．
已知：如图，OC是∠AOB的平分线，点P是OC上的任意一点，PD⊥OA，PE⊥OB，垂足分别为点D和点E．
请写出完求证：PD＝PE．
分析图中有两个直角三角形PDO和PEO，只要证明这两个三角形全等，便可证得PD＝PE．
（1）请根据教材中的分析，结合图①，写出“角平分线的性质定理”完整的证明过程．
【定理应用】
（2）如图②，已知OC是∠AOB的平分线，点P是OC上的任意一点，点D、E分别在边OA、OB上，连结PD、PE，∠AOB+∠DPE＝180°．若∠AOB＝60°，OD+OE＝5，则OP的长为 ．
（3）如图③，在平行四边形ABCD中，∠ABC＝60°，BE平分∠ABC交AD于点E，连结CE，将CE绕点E旋转，当点C的对应点F落在边AB上时，若BF+BC＝12，则四边形BCEF的面积为 ．

解题大招：全等常见模型：
①K型图：
图形
条件与结论
辅助线
注意事项
条件：AC=BC,AC⊥BC
结论：
△ADC≌△CEB(AAS)
分别过点A、B作AD⊥l,
BE⊥l
K型图可以和等腰直角三角板结合，也可以和正方形结合
K型全等模型变形——三垂定理：
如图，亦有△ADC≌△CEB(AAS)
总结：当一个直角放在一条直线上时，常通过构造K型全等来证明边相等，或者边之间的数量关系

②手拉手：
模型名称
几何模型
图形特点
具有性质
全
等
型
手
拉
手
AD=AE
AB=AC
∠BAC=∠DAE
连结BD、CE
①△ABD≌△ACE
②△AOB∽△HOC
③旋转角相等
（即∠1=∠2=∠3）
④A、B、C、D四点共圆
⑤AH平分∠BHE
③倍长中线：
基本图形
辅助线
条件与结论
应用环境
延长AD到点E，
使DE=AD，连接CE
条件：△ABC，AD=BD
结论：
△ABD≌△CED(SAS)
①倍长中线常和△三边关系结合，考察中线长的取值范围
②倍长中线也可以和其他几何图形结合，考察几何图形的面积问题
解题大招：相似常见模型：
①A字图：
当DE∥BC时
△ADE∽△ABC
性质：
当∠ADE=∠ACB时
△ADE∽△ACB
性质：
变型

②8字图：当∠A=∠C时
△AJB∽△CJD
性质：
当AB∥CD时
△AOB∽△DOC
性质：
变型
③一线三等角：

一般地：当动点E运动到底边的中点时，CF有最大值
在Rt△ACB与Rt△ADC中，当∠ABC=∠ACD时，有
Rt△ACB∽Rt△ADC∽Rt△CDB
射影定理：
特殊母子型——射影定理
☆：有关射影定理图形常见的三个应用方向：
等积法（求斜边上的高）
同角的余角相等（得∠A=∠BCD）
射影定理
在圆中因为直径所对圆周角=90°，转化得此图形，进而利用以上3个结论！
☆：“母子△”与“阿氏圆”
阿氏圆的基本原理就是构造母子三角形，之后再结合两点之间线段最短求解最后结果。具体步骤等见最值小专题“阿氏圆”！
课题
测量旗杆的高度
成员
组长：×××
组员：×××，×××，×××
测量工具
皮尺，标杆
测量示意图

说明：在水平地面上直立一根标杆EF，观测者沿着直线BF后退到点D，使眼睛C、标杆的顶端E、旗杆的顶端A在同一直线上．
测量数据
观测者与标杆的距离DF
观测者与旗杆的距离DB
标杆EF的长
观测者的眼睛离地面的距离CD
1m
18m
2.4m
1.6m
问题解决
如图，过点C作CH⊥AB于点H，交EF于点G．…
解题大招：常见组合模型
①知2得1：
①AD为角平分线；②DE∥AB；③AE=ED
若以上3个条件中有2个成立，则剩余的那个就会成立。即：三条件满足“知2得1”


②勾股定理面积应用：
图形
结论
总结
当分别以直角三角形的三边为边（或底边、半径）做规则的正方形、等边三角形、等腰直角三角形、半圆时，均满足两直角边所做图形的面积和等于斜边所做图形的面积
A
C
D
B
E
E
D
B
C
A
F
③等腰直角三角形中“半角模型”
☆1：若∠DAE旋转到△ABC外部时，结论BD2＋CE2=DE2仍然成立
E
D
B
C
A
E
D
B
C
A
F
☆2：若∠DAE=135°时，则有结论CD2＋BE2=DE2。