期中阶段测试（第1-5单元）（试题）-2023-2024学年数学六年级下册青岛版

这是一份期中阶段测试（第1-5单元）（试题）-2023-2024学年数学六年级下册青岛版，共17页。试卷主要包含了填空题，选择题，判断题，计算题，解答题等内容，欢迎下载使用。


一、填空题
1．四年级学生分组参加课外兴趣小组，每人只能参加一个小组。航模类每6人一组，阅读类每4人一组，共38人报名，正好分成8组。参加航模类的学生有( )人。
2． 把5∶3＝20∶12的内项3增加6，要使比例仍然成立，外项12应该增加( )。
3．如果5a＝7b（a与b均不为0），那么a∶b＝( )∶( )，a和b成( )比例。
4． 甲、乙两数的比是5∶4，则乙数比甲数少( )。（填百分数）
5．王宏将40000元人民币存入银行，定期5年，年利率是2.75%，到期后，王宏可以取出( )元。
6．圆柱的体积是36立方分米，把它削成一个最大的圆锥，圆锥的体积是( )立方分米。
7．如下图所示，把底面直径8厘米的圆柱切成若干等份，拼成一个近似的长方体，这个长方体的表面积比原来增加160平方厘米，那么长方体的体积是( )立方厘米。
8．张老师对实验小学六年级学生参加晚托各类活动情况进行了统计，分布情况如下图。
(1)参加体育运动一共有90人，那么本次六年级晚托学生有( )人。
(2)教室自习学生数和艺术类学生数之比是( )。
(3)学科类学生数比体育运动类学生数少( )%。
(4)如果张老师接下去几年要对参加学科类学生的数量变化情况进行统计，用( )统计图最合适。
二、选择题
9．某次数学竞赛共20道题，评分标准是：每做对一题得5分，每做错或不做一题扣1分。小华参加了这次竞赛，得了64分。小华做对（ ）道题。
A．6B．9C．11D．14
10．一种微型零件的长度是0.5毫米，画在图上的长度为10厘米。这幅图的比例尺为（ ）。
A．B．C．D．
11．下面百分率可能大于100%的是（ ）。
A．成活率B．出勤率C．增长率D．合格率
12．下面图形面积、体积公式或计算法则的推导过程，运用“转化”策略的有（ ）。

A．①和②B．②和③C．①和③D．①②③
13．红领巾气象站每两小时要测量一次气温，为了形象地表示出一天中气温的升降变化情况，应当绘制（ ）统计图最合适。
A．条形B．折线C．扇形D．以上三种都可以
三、判断题
14．要表示某小学各年级学生人数与全校学生总人数的关系，应选择扇形统计图。( )
15．中国最南边的曾母暗沙距广东省约2000千米，在比例尺为1∶200000的地图上，我们可以量得图上距离为2厘米。( )
16．《数学报》的单价一定，订阅《数学报》的份数与总价成正比例。( )
17．淘气做12道题，对了12道，他的正确率是120%。( )
18．从圆柱的前面，侧面和上面看到的都是圆形。( )
19．长方体、正方体、圆柱和圆锥体积的计算都是体积单位的累加。( )
四、计算题
20．直接写出得数。


21．解方程。

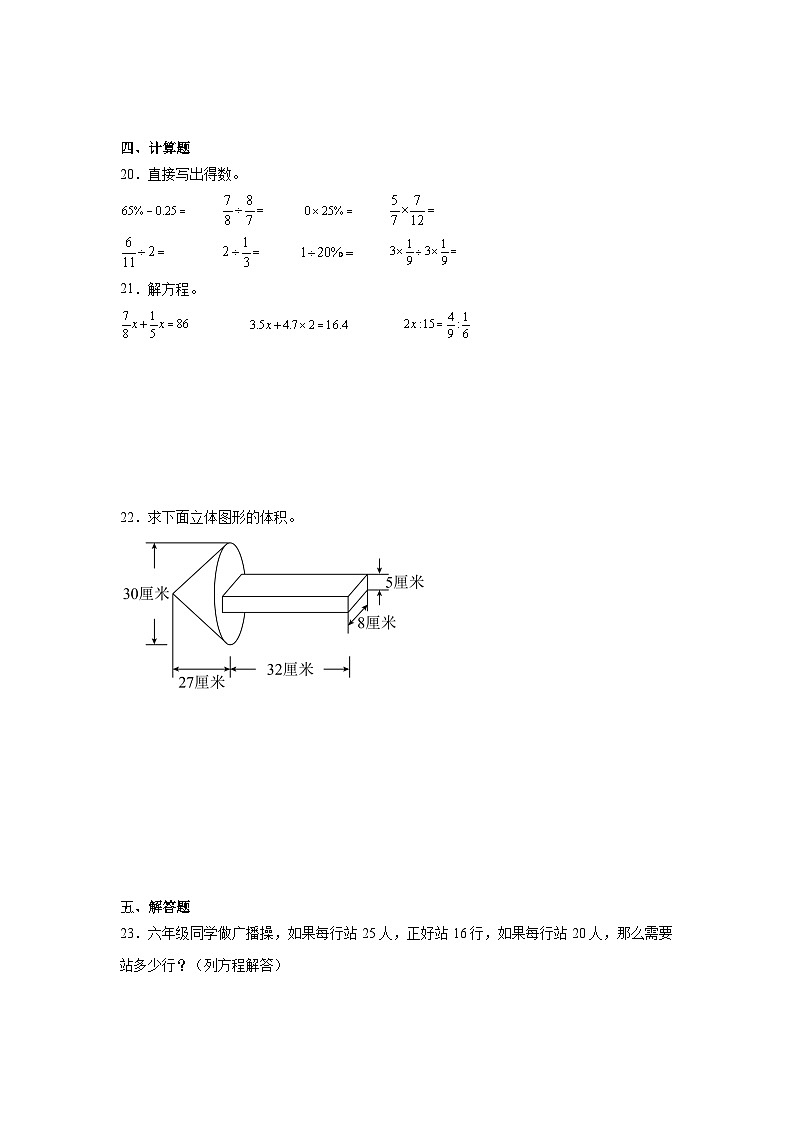
22．求下面立体图形的体积。
五、解答题
23．六年级同学做广播操，如果每行站25人，正好站16行，如果每行站20人，那么需要站多少行？（列方程解答）
24．“丝绸之路”是古代连接中西方的商道。传统的丝绸之路起自我国古代都城长安，以罗马为终点，在一幅比例尺为的地图上约长，传统的丝绸之路实际全长约为多少千米？
25．一个圆柱形水池，直径8米，深2米。
（1）这个水池占地面积是多少？
（2）在池底及池壁抹一层水泥，抹水泥部分的面积是多少？
（3）每千克水泥可涂4平方米，共需多少千克水泥？
26．一个圆柱体的高是12厘米，如果将这个圆柱体的高减少，那么它的表面积就减少37.68平方厘米，原来圆柱体的体积是多少立方厘米？
27．服装厂生产一款西装，图①是该厂第一季度三个月产量的统计图，图②是这三个月的产量占第一季度总产量的分布情况统计图。
（1）把统计图补充完整。
（2）该厂三月份产量比二月份增长百分之几？
（3）如果第一季度生产产品的合格率为98%，该厂第一季度生产合格的产品数量是多少件？
参考答案：
1．18
【分析】假设8 组都是阅读类，依此计算出8组阅读类的总人数，实际总人数与8组阅读类的总人数的差，航模类与阅读类每组的人数差，然后用实际总人数与8组阅读类的总人数的差，除以航模类与阅读类每组的人数差，得到的商就是参加航模类的组数，最后用参加航模类的组数乘每组的人数即可，依此解答。
【详解】假设8 组都是阅读类
8×4＝32（人）
38－32＝6（人）
6－4＝2（人）
6÷2＝3（组）
3×6＝18（人）
参加航模类的学生有18人。
【点睛】此题考查的是鸡兔同笼问题的计算，应熟练掌握应用假设法解答此类题型，先计算出参加航模组的组数，是解题的关键。
2．24
【分析】根据比例的基本性质，内项3增加6，扩大到原来的3倍；要使比例仍然成立，外项12应该扩大到原来的3倍，再减去12，即可解答。
【详解】（3＋6）÷3
＝9÷3
＝3
12×3－12
＝36－12
＝24
把5∶3＝20∶12的内项3增加6，要使比例仍然成立，外项12应该增加24。
3． 7 5 正
【分析】根据比例的基本性质，在比例里，两个外项的积等于两个内项的积。如果5a＝7b（a、b均不为0），把5和a看作比例的两个外项，把7和b看作比例的两个内项，据此写出比例，即可得解；判断两个相关联的量之间成什么比例，就看这两个量是对应的比值一定，还是对应的乘积一定；如果是比值一定，就成正比例；如果是乘积一定，则成反比例。
【详解】如果5a＝7b（a与b均不为0），那么a∶b＝7∶5。
a∶b＝7∶5＝7÷5＝1.4
可得a和b的比值一定，所以a和b成正比例。
【点睛】此题主要考查比例的基本性质以及辨识成正、反比例的两个量。
4．20%
【分析】甲、乙两数的比是5∶4，则把甲看作5份，乙看作4份；要求乙数比甲数少百分之几，就是用甲数减去乙数，求出差，再除以甲数即可。
【详解】（5－4）÷5×00%
＝1÷5×100%
＝0.2×100%
＝20%
乙数比甲数少20%
5．45500
【分析】根据“利息＝本金×利率×存期”，求出到期后可以得到的利息，再加上本金，就是到期后一共可以取出的钱数。
【详解】40000×2.75%×5＋40000
＝40000×0.0275×5＋40000
＝1100×5＋40000
＝5500＋40000
＝45500（元）
到期后，王宏可以取出45500元。
【点睛】本题考查利率问题，掌握利息的计算方法并灵活运用是解题的关键。
6．12
【分析】
把一个圆柱削成最大的圆锥，那么圆柱和圆锥的底面积和高相等，因此圆柱的体积就是圆锥体积的3倍，所以圆锥的体积是圆柱体积的；据此解答。
【详解】36×＝12（立方分米）
圆锥的体积是12立方分米。
7．1004.8
【分析】根据圆柱体积公式的推导过程可知，把一个圆柱切拼成一个近似长方体，这个长方体的底面积等于圆柱的底面积，长方体的高等于圆柱的高，拼成的长方体的比圆柱的表面积增加了两个切面的面积，每个切面的长等于圆柱的高，每个切面的宽等于圆柱的底面半径，根据增加的表面积可以求出圆柱的高，然后根据圆柱的体积公式：V＝πr2h，把数据代入公式解答。
【详解】160÷2÷（8÷2）
＝160÷2÷4
＝80÷4
＝20（厘米）
3.14×（8÷2）2×20
＝3.14×42×20
＝3.14×16×20
＝50.24×20
＝1004.8（立方厘米）
长方体的体积是1004.8立方厘米。
8．(1)450
(2)11∶2
(3)25
(4)折线
【分析】（1）将总人数看作单位“1”，体育运动人数÷对应百分率＝总人数；
（2）1－体育运动对应百分率－艺术类对应百分率－学科类对应百分率＝教室自习对应百分率，根据比的意义，写出教室自习和艺术类对应百分率的比，化简即可；
（3）学科类和体育运动类对应百分率的差÷体育运动类对应百分率＝学科类学生数比体育运动类学生数少百分之几；
（4）折线统计图不仅能看清数量的多少，还能通过折线的上升和下降表示数量的增减变化情况，据此选择统计图。
【详解】（1）90÷20%＝90÷0.2＝450（人），本次六年级晚托学生有450人。
（2）1－20%－10%－15%＝55%，55%∶10%＝55∶10＝11∶2，教室自习学生数和艺术类学生数之比是11∶2。
（3）（20%－15%）÷20%
＝0.05÷0.2
＝0.25
＝25%
学科类学生数比体育运动类学生数少25%。
（4）如果张老师接下去几年要对参加学科类学生的数量变化情况进行统计，用折线统计图最合适。
【点睛】利用扇形统计图解决问题，就是解决有关不同类型的百分数应用题，按照百分数相关解题思路解答即可。
9．D
【分析】假设全部做对，应得5×20分，比实际得分多了（5×20－64）分，因为每道错题多算了（5＋1）分，比实际多得的分数÷每道错题多算的分数＝错题数，总题数－错题数＝做对的题数。
【详解】（5×20－64）÷（5＋1）
＝（100－64）÷6
＝36÷6
＝6（道）
20－6＝14（道）
小华做对14道题。
故答案为：D
10．D
【分析】根据比例尺图上距离∶实际距离，将单位化为一致，1厘米＝10毫米，代入数据解答即可。
【详解】10厘米∶0.5毫米
毫米∶0.5毫米
即这幅图的比例尺为。
故答案为：D
11．C
【分析】××率＝要求量（就是××所代表的信息）÷单位“1”的量（总量）×100%，据此分析要求量与总量之间的关系即可。
【详解】A．成活率＝成活数÷总数×100%，成活数不可能大于总数，成活率不可能大于100%；
B．出勤率＝出勤人数÷总人数×100%，出勤人数不可能大于总人数，出勤率不可能大于100%；
C．增长率＝增长幅度÷原来的量×100%，增长幅度有可能超过原来的量，增长率有可能大于100%；
D．合格率＝合格数÷总数×100%，合格数不可能大于总数，合格率不可能大于100%。
百分率可能大于100%的是增长率。
故答案为：C
12．D
【分析】“转化”策略是指把一个数学问题变更为一类已经解决或比较容易解决的问题，从而使原问题得以解决的一种策略。据此分析各个推导过程，判断是否使用了“转化”策略，从而解题。
【详解】①将求平行四边形面积转化成求长方形的面积，体现了“转化”策略；
②将小数乘小数先按照整数乘法计算，再点小数点，小数乘法先转换为整数乘法计算，也体现了“转化”策略；
③将求圆柱的体积变成求近似长方体的体积，体现了“转化”策略。
所以，运用“转化”策略的有①②③。
故答案为：D
【点睛】本题考查了平行四边形面积的推导、小数乘小数的计算方法以及圆柱体积公式的推导，掌握推导过程和“转化”策略的概念是解题的关键。
13．B
【分析】根据各个统计图的特点，结合题中统计需求，直接选出正确选项即可。
【详解】折线统计图可以清晰反映数据的变化情况，所以要形象地表示出一天中气温的升降变化情况，应当绘制折线统计图最合适。
故答案为：B
【点睛】本题考查了统计图的选择，明确常见统计图的特点是解题的关键。
14．√
【分析】条形统计图能很容易看出数量的多少；折线统计图不仅容易看出数量的多少，而且能反映数量的增减变化情况；扇形统计图能反映部分与整体的关系。
【详解】某小学各年级学生人数与全校学生总人数的关系是反映部分与整体的关系，应选择扇形统计图。
故答案为：√
15．×
【分析】根据图上距离∶实际距离＝比例尺，可得图上距离＝实际距离×比例尺。用曾母暗沙距广东省的实际距离×比例尺，即可求出两地的图上距离。据此解答。
【详解】2000千米＝200000000厘米
2000000001000（厘米）
两地的图上距离为1000厘米。
故答案为：×
16．√
【分析】x÷y＝k（一定），x和y成正比例关系；xy＝k（一定），x和y成反比例关系，据此分析。
【详解】总价÷份数＝单价，《数学报》的单价一定，订阅《数学报》的份数与总价成正比例，说法正确。
故答案为：√
17．×
【分析】根据正确率＝正确的道数÷总道数×100%，计算即可判断。
【详解】12÷12×100%
＝1×100%
＝100%
所以题干说淘气做12道题，对了12道，他的正确率是120%，错误。
故答案为：×
18．×
【分析】圆柱上下面是圆形，侧面是曲面；从圆柱的前面，侧面看到的是长方形（或正方形），上面看到的是圆形。
【详解】由题意分析得：
从圆柱的侧面看到的不是圆形。原题说法错误。
故答案为：×
19．√
【详解】根据长方体体积公式的推导过程：沿着长、宽、高摆放一个一个的正方体，一个小正方体就是一个体积单位，沿着长摆，可知一行可以摆放几个正小方体，沿着宽摆，可知摆了几行，这两个数相乘，即可求出一层摆多少个正方体，再沿着高摆，可知摆了几层，所以用一层摆的个数乘高摆的层数，即可求出摆了多少个小正方体，这些小正方体的个数就是长方体的体积，由此可知长方体的体积就是一个一个正方体累加起来的，一个一个的小正方体就是一个一个的体积单位，所以长方体的体积就是体积单位累加的。正方体和圆柱、圆锥的体积都是由长方体的体积公式推导的，所以长方体、正方体、圆柱和圆锥体积的计算都是体积单位的累加。所以原题说法正确。
故答案为：√
20．0.4；；0；；
；6；5；
【详解】略
21．；；
【分析】（1）先把方程化简成，然后方程两边同时除以，求出方程的解；
（2）先把方程化简成，然后方程两边先同时减去9.4，再同时除以3.5，求出方程的解；
（3）先根据比例的基本性质把比例方程改写成，再化简成，然后方程两边同时除以，求出方程的解。
【详解】（1）
解：
（2）
解：
（3）
解：
22．7638.5立方厘米
【分析】图中立体图形的体积等于圆锥体体积加上长方体体积，根据圆锥体的体积，长方体的体积＝长×宽×高，即可算出图中立体图形的体积。
【详解】圆锥体体积：
（立方厘米）
长方体体积：
（立方厘米）
图中立体图形的体积：6358.5＋1280＝7638.5（立方厘米）
23．20行
【分析】根据题意知道，六年级同学的总人数一定，每行站的人数和行数成反比例，设如果每行站20人，需要站x行，列比例：20x＝25×16，解比例，即可解答。
【详解】解：设如果每行站20人，需要站x行。
20x＝25×16
20x＝400
20x＝400÷20
x＝20
答：需要站20行。
24．644千米
【分析】图上距离和比例尺已知，利用“实际距离图上距离比例尺”即可求得两地的实际距离，注意换算单位，1千米＝100000厘米，低级单位转化为高级单位用除法，只需要将原数的末尾去掉5个0即可。
【详解】（厘米）
64400000厘米千米
答：传统的丝绸之路实际全长约为644千米。
25．（1）50.24平方米
（2）100.48平方米
（3）25.12千克
【分析】（1）水池的占地面积就是这个圆柱形水池的底面积，根据圆的面积公式：S＝πr2，把数据代入公式解答；
（2）水泥面的面积相当于圆柱的表面积，水池没有上边的面，用一个底面积＋侧面积即可。
（3）用这个水池抹水泥部分的面积除以4进行计算即可得到答案。
【详解】（1）3.14×（8÷2）2
＝3.14×16
＝50.24（平方米）
答：这个水池占地面积是50.24平方米。
（2）50.24＋3.14×8×2
＝50.24＋25.12×2
＝50.24＋50.24
＝100.48（平方米）
答：抹水泥部分的面积是100.48平方米。
（3）100.48÷4＝25.12（千克）
答：共需25.12千克水泥。
26．150.72立方厘米
【分析】高减少厘米后圆柱的表面积减少37.68平方厘米，先求减少的圆柱的高，用12×＝3（厘米），表面积减少的是3厘米的侧面积，用37.68除以3求出底面周长，用底面周长除以圆周率除以3求出底面半径，然后根据圆柱的体积公式：v＝sh，把数据代入公式解答。
【详解】减少的圆柱的高：12×＝3（厘米），
底面半径是：
37.68÷3÷3.14÷2
＝12.56÷3.14÷2
＝2（厘米）
原来的体积是：
3.14×22×12
＝3.14×4×12
＝150.72（立方厘米）
答：原来体积是150.72立方厘米。
【点睛】抓住切割特点，得出减少的表面积是减少的圆柱部分的侧面积，从而求出底面半径是解决本题的关键。
27．（1）见详解
（2）18.75%
（3）4900件
【分析】（1）根据图示可知二月份生产1600件西装，占三个月的32%，用二月份生产的件数除以二月份占总件数的百分率，据此可以求出三个月一共生产西装的件数，再把总件数看作单位“1”，用单位“1”减去二月、三月生产占总件数的百分率，求出一月份占总件数的百分率；最后用三个月的总件数乘一月份生产占总件数的百分率，求出一月份的产量，把统计图补充完整即可。
（2）用该厂三月份产量比二月份增长的数量除以二月份的产量，解答即可。
（3）根据题意，用第一季度的总产量乘第一季度生产产品的合格率，解答即可。
【详解】（1）1600÷32%×（1－38%－32%）
＝5000×30%
＝1500（件）
把统计图补充完整如下：
（2）（1900－1600）÷1600×100%
＝300÷1600×100%
＝0.1875×100%
＝18.75%
答：该厂三月份产量比二月份增长18.75%。
（3）（1500＋1600＋1900）×98%
＝（3100＋1900）×98%
＝5000×98%
＝4900（件）
答：该厂第一季度生产合格的产品数量是4900件。