




江苏省南京市建邺区南京师范大学附属中学新城初级中学2023-2024学年八年级下学期4月月考数学试题(原卷版+解析版)
展开一、选择题(本大题共6小题,每小题2分,共12分.在每小题所给出的四个选项中,恰有一项是符合题目要求的,请将正确选项的字母代号填涂在答题卡相应位置上)
1. 下列电视台的台标,是中心对称图形的是( )
A. B. C. D.
【答案】D
【解析】
【分析】根据把一个图形绕某一点旋转,如果旋转后的图形能够与原来的图形重合,那么这个图形就叫做中心对称图形可得答案。
【详解】根据中心对称图形的概念,四个选项中只有D符合.
故选:D.
【点睛】本题考查了中心对称图形,掌握中心对称图形的概念是解题的关键。
2. 分式可变形为( )
A. B. C. D.
【答案】D
【解析】
【详解】试题分析:根据分式的性质,分子分母都乘以﹣1,分式的值不变,可得答案:
分式的分子分母都乘以﹣1,得.
故选D.
考点:分式的基本性质.
3. 要把分式的值扩大为原来的3倍,下面哪种方法是可行的( )
A. 、的值都加上3B. 、的值都扩大为原来的3倍
C. 的值不变、的值扩大为原来的3倍D. 的值扩大为原来的3倍、y的值不变
【答案】B
【解析】
【分析】根据分式的性质,逐一判断各个选项,即可得到答案.
【详解】解:A. 、的值都加上3,分式的值不会扩大为原来的3倍 ,不符合题意;
B. 、的值都扩大为原来的3倍,分式的值扩大为原来的3倍,符合题意;
C. 的值不变、的值扩大为原来的3倍,分式的值不会扩大为原来的3倍 ,不符合题意;
D. 的值扩大为原来的3倍、y的值不变,分式的值不会扩大为原来的3倍 ,不符合题意.
故选B.
【点睛】本题主要考查分式的基本性质,能够正确利用分式的性质变形是解题的关键.
4. 如图,矩形中,,,是边的中点,是边上的一动点,、分别是、的中点,随着点的运动,线段长( )
A. 随着点的位置变化而变化B. 保持不变,长为
C. 保持不变,长为D. 保持不变,长为
【答案】C
【解析】
【分析】连接AP,根据矩形的性质求出AP的长度,再根据三角形的中位线平行于第三边并且等于第三边的一半可得MN=AP,问题得解.
【详解】解:连接AP,
∵矩形ABCD中,AB=DC=2,AD=,P是CD边上的中点,
∴DP=1,
∴AP== ,
∵M,N分别是AE、PE的中点,
∴MN是△AEP的中位线,
∴MN=AP=,保持不变.
故选:C.
【点睛】本题考查了矩形的性质,三角形的中位线平行于第三边并且等于第三边的一半,熟记性质以及定理并求出AP的值是解题的关键.
5. 如图,两个正方形的边长都为6,其中正方形OEFG绕着正方形ABCD对角线的交点O旋转,正方形OEFG与边AB,BC分别交于点M,N(不与端点重合),设两个正方形重叠部分的面积为m,ΔBMN的周长为n,则下列说法正确的是( )
A. m发生变化,n存在最大值
B. m发生变化,n存在最小值
C. m不发生变化,n存在最大值
D. m不发生变化,n存在最小值
【答案】D
【解析】
【分析】由“ASA”可证△AOM≌△BON,可得OM=ON,AM=BN,S△AOM=S△CON,可得mS正方形ABCD=9,由n=BM+BN+MN=AM+BM+MN=6+MN,可得当MN有最小值时,n有最小值,即可求n值.
【详解】解:∵正方形ABCD的对角线AC,BD交于点O,
∴OC=OD=BO=AO,∠BAO=∠CBO=45°,AC⊥BD.
∵∠MOA+∠BOM=90°,∠BON+∠BOM=90°
∴∠AOM=∠BON,
在△AOM和△CON中,
,
∴△AOM≌△BON(ASA)
∴OM=ON,AM=BN,S△AOM=S△CON,
∴两个正方形重叠部分形成图形的面积=S△BOM+S△BON=S△AOB,
∴mS正方形ABCD=9,
∵△BMN的周长为n,
∴n=BM+BN+MN=AM+BM+MN=6+MN,
∴当MN有最小值时,n有最小值,
∵OM=ON,∠MON=90°,
∴MNOM,
∴当OM⊥AB时,OM有最小值为3,
∴n的最小值为6+3,
因为点M不与点A,B重合,所以OM不存在最大值,所以MN不存在最大值,所以n不存在最大值,
故选:D.
【点睛】本题考查了旋转的性质,全等三角形的判定和性质,勾股定理,正方形的性质,证明△AOM≌△BON是解题的关键.
6. 如图,在中,,,,P是边上一动点,连接,把线段绕点A逆时针旋转到线段,连接,则线段的最小值为( )
A. B. C. D.
【答案】B
【解析】
【分析】在上取一点E,连接,证明,得出,说明要使最小,则有最小,点P是上的动点,根据垂线段最短,得出当(点P和点F重合)时,最小,求出最小值即可.
【详解】解:如图,在上取一点E,连接,
由旋转知,,
∵,
∴,
∴,
∴,
∴,
∴,
要使最小,则有最小,点P是上的动点,
∴当(点P和点F重合)时,最小,
即:点P与点F重合,最小,
在中,,
∴,
∵,
∴,
在中,,
∴,
故线段长度最小值是,
故选:B.
【点睛】此题主要考查了旋转的性质,全等三角形的判定和性质,含30°角的直角三角形的性质等,找出点P和点F重合时,EQ最小,最小值为EF的长度是解本题的关键.
二、填空题(本大题共10小题,每小题2分,共20分.不需写出解答过程,请把答案直接填写在答题卡相应的位置上)
7. 若式子在实数范围内有意义,则的取值范围是________.
【答案】
【解析】
【分析】分式若有意义,则分式的分母不能为,据此可求得答案.
【详解】解:若式子在实数范围内有意义,则
.
解得
.
故答案为:.
【点睛】本题主要考查分式有意义的条件(分式的分母不能为),牢记分式有意义的条件是解题的关键.
8. 分式、的最简公分母是________.
【答案】##
【解析】
【分析】确定最简公分母的方法是:(1)取各分母系数的最小公倍数;(2)凡单独出现的字母连同它的指数作为最简公分母的一个因式;(3)同底数幂取次数最高的,得到的因式的积就是最简公分母.
【详解】解:分式、的最简公分母是,
故答案为:.
【点睛】本题考查了最简公分母,确定最简公分母的方法一定要掌握.
9. 不改变分式的值,把分式的分子与分母中各项的系数都化为整数,结果为_____.
【答案】
【解析】
【分析】本题考查了分式的化简,根据分式的性质,分子分母同时乘以一个不为的整式,分式的值不变,只需将分式的分子和分母同时乘即可求解,掌握分式的性质是解题的关键.
【详解】解:,
故答案为:.
10. 关于x的方程有增根,则m的值是______.
【答案】
【解析】
【分析】此题主要考查了分式方程的增根,要熟练掌握,解答此题的关键是要明确:(1)化分式方程为整式方程;(2)把增根代入整式方程即可求得相关字母的值.首先把所给的分式方程化为整式方程,然后根据分式方程有增根,得到,据此求出的值,代入整式方程求出的值即可.
【详解】解:去分母,得:,
由分式方程有增根,得到,即,
把代入整式方程,可得:.
故答案为:
11. 如图所示,菱形中,对角线相交于点O,若再补充一个条件能使菱形成为正方形,则这个条件是_____.(只填一个条件即可)
【答案】(答案不唯一)
【解析】
【分析】本题主要考查了正方形的判定.根据菱形的性质及正方形的判定来添加合适的条件,即可.
【详解】解:添加,理由:
∵四边形是菱形,,
∴四边形是正方形.
故答案为:(答案不唯一)
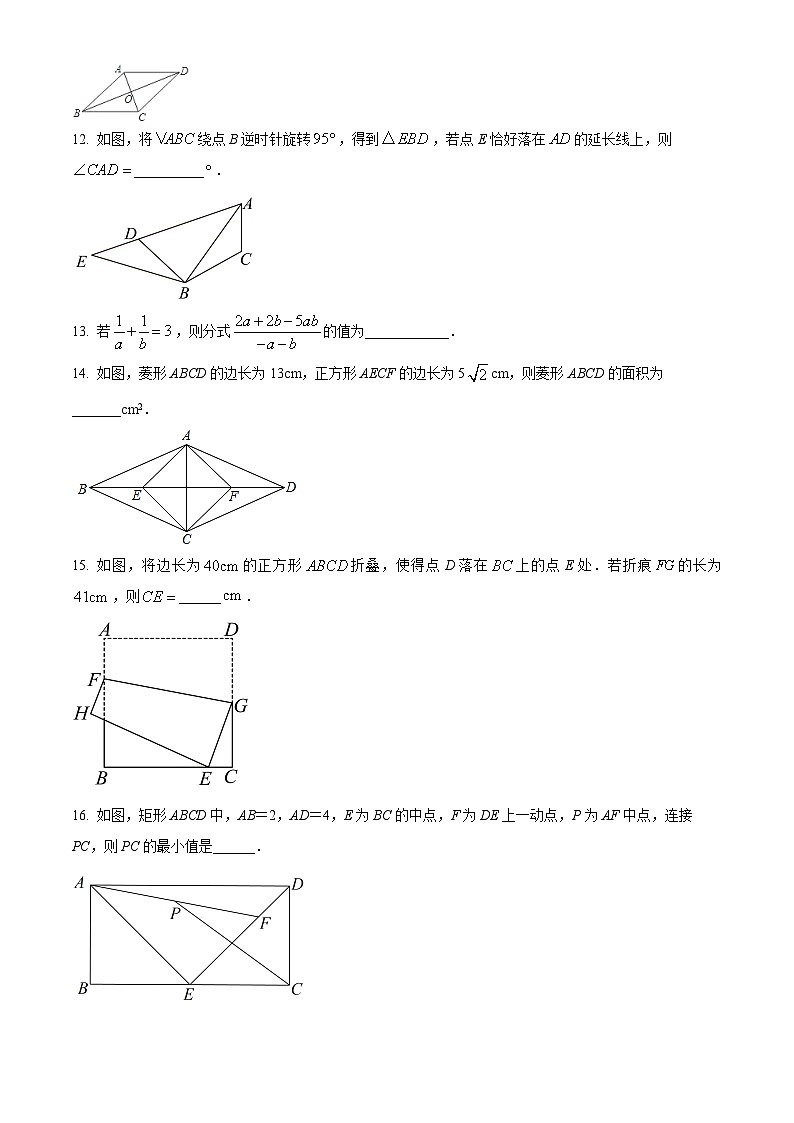
12. 如图,将绕点B逆时针旋转,得到,若点E恰好落在的延长线上,则__________.
【答案】85
【解析】
【分析】利用旋转性质得出旋转前后对应线段相等、对应角相等即可.
【详解】解:∵将△ABC绕点B逆时针旋转95°,
∴∠ABE=95°,AB=BE,∠CAB=∠E,
∵AB=BE,
∴∠E=∠BAE,
∴∠BAE+∠CAB=∠BAE+∠E=180°−∠ABE
=180°−95°
=85°,
故答案为:85.
【点睛】本题主要考查了旋转的性质以及三角形内角和定理的应用,熟记旋转的性质是解决问题的关键.
13. 若,则分式的值为____________.
【答案】
【解析】
【分析】由可得,再将所求分式的分子、分母化为含有的代数式,进而整体代换求出结果即可.
【详解】解:∵,
∴,
∴,
∴
.
故答案为:.
【点睛】本题考查分式的求值,分式的加减,分式的约分,运用了整体代换思想解题.掌握分式的加减法是解题的关键.
14. 如图,菱形ABCD的边长为13cm,正方形AECF的边长为5cm,则菱形ABCD的面积为_______cm2.
【答案】120
【解析】
【分析】由正方形的性质可求AC的长,由勾股定理可求BO的值,可求BD的值,即可求菱形ABCD的面积.
【详解】解:如图,
∵正方形AECF的边长为5cm,
∴AC=EF=10cm,AO=5cm,
∵四边形ABCD是菱形,
∴AC⊥BD,BO=DO,
∴BO==12cm,
∴BD=2BO=24cm,
∴菱形ABCD的面积=AC×BD=120cm2.
故答案为:120.
【点睛】本题考查正方形的性质,菱形的性质,勾股定理,熟练运用正方形的性质是本题的关键.
15. 如图,将边长为的正方形折叠,使得点D落在上的点E处.若折痕的长为,则______.
【答案】9
【解析】
【分析】本题考查正方形中的折叠问题,矩形的判定和性质,全等三角形的判定和性质,作于P,连接,易得四边形是矩形,证明,得到,再利用勾股定理进行求解即可.
【详解】解:∵四边形是正方形,
∴,
作于P,连接,
则四边形是矩形,
∴,,
由翻折知,,
∴,
∴,
∴,
在中,由勾股定理得,
故答案为:9.
16. 如图,矩形ABCD中,AB=2,AD=4,E为BC的中点,F为DE上一动点,P为AF中点,连接PC,则PC的最小值是______.
【答案】
【解析】
【分析】取AD中点H,连接BH,CH,设BH与AE的交点为O,连接CO,可证四边形DEBH是平行四边形,可得,由三角形中位线定理可得,可得点P在BH上,当CP⊥BH时,PC有最小值,即可求解.
【详解】解:如图,取AD中点H,连接BH,CH,设BH与AE的交点为O,连接CO,如图所示:
∵四边形ABCD是矩形,
∴AB=CD=2,AD=BC=4,,,
∵点E是BC中点,点H是AD中点,
∴AH=CE=DH=BE=AB=CD=2,
∴四边形BEDH是平行四边形,,
,
∴,
∵点P是AF的中点,点H是AD的中点,
∴,
∴点P在BH上,
∵,
∴,
∴,
∵点P在BH上,
∴当CP⊥BH时,此时点P与H重合,PC有最小值,
在Rt△CDH中,
∴PC的最小值为,
故答案为:.
【点睛】本题考查了矩形的性质,三角形中位线定理,等腰直角三角形的性质,平行四边形的性质,垂线段最短等知识,确定点P的运动轨迹是本题的关键.
三、解答题(本大题共10小题,共68分,请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤)
17. (1).
(2)先化简,再从中选一个合适的整数代入求值.
【答案】(1);(2),时,原式=.
【解析】
【分析】本题考查了分式的混合运算和化简求值.
(1)先进行分式的除法运算,再进行分式的减法运算即可;
(2)根据分式运算法则先化简,再代入已知条件中的值计算即可.
【详解】解:(1)
;
解:
当时,原式
18. (1)解分式方程:;
(2)若关于分式方程的解为正数,则的取值范围是______.
【答案】(1)无解;(2)且.
【解析】
【分析】(1)先去分母化成整式方程,然后求解,最后检验即可;
(2)先解关于x的分式方程得到关于m的不等式,然后求出m的取值范围即可.
【详解】(1)解:,
,
x=1
检验:当时,,
∴是原方程的增根,∴原方程无解.
(2)解:
,
∵原方程解为正数,
∴且,
∴且.
【点睛】本题主要考查了解分式方程,掌握解分式方程方法和步骤成为解答本题的关键.
19. 小明去图书馆借书,到达后发现借书卡没带,于是他跑步回家,拿到借书卡后骑车返回图书馆.已知图书馆离小明家1650m,小明骑车时间比跑步时间少5.5 min,且骑车的平均速度是跑步的平均速度的1.5倍,求小明跑步的平均速度.
【答案】100m/min
【解析】
【分析】设小明跑步的平均速度为xm/min,根据题意列出分式方程并求解即可.
【详解】解:设小明跑步的平均速度为xm/min.
由题意得,
解得:
答:小明跑步的平均速度为100m/min.
【点睛】本题主要考查分式方程的应用,根据题意正确列出分式方程是解题的关键.
20. 如图,在四边形ABCD中,AD=BC,P是四边形ABCD外一点,且PA=PD,PB=PC,∠APB=∠DPC.
(1)求证:∠ABC=∠DCB;
(2)求证:四边形ABCD是矩形.
【答案】(1)见解析 (2)见解析
【解析】
【分析】(1)由全等三角形的判定定理SAS推知△ABP≌△DCP,根据该全等三角形的对应角相等、等腰三角形的性质推知∠ABC=∠DCB;
(2)由“有一内角是直角的平行四边形为矩形”证得结论.
【小问1详解】
解:证明:在△ABP和△DCP中,
,
∴△ABP≌△DCP(SAS).
∴∠ABP=∠DCP.
∵PB=PC,
∴∠PBC=∠PCB.
∴∠ABP+∠PBC=∠DCP+∠PCB.
即∠ABC=∠DCB;
【小问2详解】
证明:∵△ABP≌△DCP,
∴AB=CD.
∵AD=BC,AB=CD,
∴四边形ABCD是平行四边形,
∴AB∥DC.
∴∠ABC+∠DCB=180°.
∵∠ABC=∠DCB,
∴2∠ABC=180°.即∠ABC=90°.
∴四边形ABCD是矩形.
【点睛】此题主要考查了矩形的判定,全等三角形的判定与性质以及等腰三角形的性质,关键是掌握有一内角是直角的平行四边形为矩形.
21. 请仔细阅读下面材料,然后解决问题:
在分式中,对于只含有一个字母的分式,当分子的次数大于或等于分母的次数时,我们称之为“假分式”,例如:,;当分子的次数小于分母的次数时,我们称之为“真分式”,例如:,.例如:假分式可以化为整式与真分式和的形式,例如:.
(1)将分式化为整式与真分式和的形式,并求出当x取哪些整数值时,分式的值也是整数?
(2)将假分式化成整式和真分式的和的形式.
【答案】(1),当、2、、4,原分式的值也是整数
(2)
【解析】
【分析】本题主要考查了分式加减运算,约分,解题的关键是熟练掌握运算法则,准确计算.
(1)仿照阅读材料中的方法将原式变形即可;原式变形后,根据结果为整数确定出整数x的值即可;
(2)仿照阅读材料中的方法将原式变形即可.
【小问1详解】
解:
.
当、2、,4,原分式的值也是整数.
【小问2详解】
解:
.
22. 如图,在中,,是的中位线,是的中线.求证:.
(1)请把证法1补充完整;
(2)试用不同的方法证明.
【答案】(1);
(2)见解析
【解析】
【分析】本题考查的是三角形中位线定理、矩形的判定和性质,掌握三角形的中位线平行于第三边,且等于第三边的一半是解题的关键.
(1)根据三角形中位线定理得到,根据直角三角形的性质得到,等量代换证明结论;
(2)连接、,根据三角形中位线定理得到,证明四边形是矩形,根据矩形的对角线相等证明即可.
【小问1详解】
解:∵是的中位线,
∴,
∵是的中线,,
∴,
∴;
故答案为:.
【小问2详解】
连接、,
∵是的中位线,是的中线,
∴、是的中位线,
∴,
∴四边形是平行四边形,
∵,
∴四边形是矩形,
∴.
23. 如图,在中,.用直尺和圆规作图:(不写作法,保留作图痕迹.)
(1)如图①,若点在边上,求作平行四边形,使得点、分别在、上;
(2)如图②,求作正方形,使得点、、分别在、、上.
【答案】(1)见解析 (2)见解析
【解析】
【分析】(1)根据过直线外一点作平行线的作法,过点D作的平行线交于为E,得到,然后以C为顶点,在上截取线段,使,连接,即可得到平行四边形;
(2)根据角平分线的作法,作出的角平分线,交于点F,连接,作线段的垂直平分线,分别与、交于点、,根据垂直平分线的性质,得到,又因为,即可证明四边形是正方形.
【小问1详解】
解:平行四边形即为所求;
【小问2详解】
解:正方形即为所求.
【点睛】本题考查了复杂作图——过直线外一点作平行线、角平分线、垂直平分线,平行四边形的额判定,正方形的判定,熟练掌握基本的作图方法是解题关键.
24. 如图,在正方形中,为对角线上一点,连接,过点作交直线于点.
(1)求证:;
(2)探究:当线段与正方形的某条边的夹角是时,的度数是多少?直接写出结果______.
【答案】(1)证明见解析
(2)或.
【解析】
【分析】本题主要考查正方形的性质、等腰直角三角形的判定与性质、全等三角形的判定与性质,解题关键是正确作出辅助线,利用全等三角形的性质解决问题.
(1)过点作,交的延长线于点,易得为等腰直角三角形,则,,再根据同角的余角相等可得,进而利用证明,以此可得证;
(2)分线段与边的夹角为和线段与边的夹角为,结合图形即可求解.
【小问1详解】
证明:过点作,交的延长线于点,如图,
四边形为正方形,
,
,
,
为等腰直角三角形,
,
,
,
,
,
在和中,
,
,
;
【小问2详解】
解:当线段与边的夹角为时,即,
,
四边形的内角和为,
;
当线段与边的夹角为时,即,
此时点在的延长线上,
如图,设与交于点,
,,
,
又,
.
综上,的度数是或.
故答案为:或.
25. 数学课上老师让学生们折矩形纸片.由于折痕所在的直线不同,折出的图形也不同,所以各个图形中所隐含的“基本图形”也不同.我们可以通过发现基本图形,来研究这些图形中的几何问题.
问题解决
(1)问题1,把一张矩形纸片按如图方式折叠,使顶点和点重合,折痕为.连接,求证:四边形是菱形;
拓展研究
(2)在(1)的条件下,若,.直接写出线段的长为 .
综合探究:
(3)如图2,是一张矩形纸片,,,在矩形的边上取一点(不与和点重合),在边上取一点(不与和点重合),将纸片沿折叠,使线段与线段交于点,得到,请你确定面积的最大值为 .
【答案】(1)证明见解析;(2);(3)
【解析】
【分析】本题是四边形的综合题,主要考查了勾股定理、平行四边形的判定、菱形的判定和性质,熟练掌握菱形的判定和性质定理,勾股定理是解题的关键.
(1)证得,得四边形是平行四边形,得四边形是菱形;
(2)连接,得,利用四边形是菱形的面积,易得的长;
(3)如图3,当点与点重合时,的面积最大,作于,则,由题意得:,设,则;根据勾股定理和三角形的面积公式即可得到结论.
【详解】(1)证明:由折叠性质可得,
,
,
,
,
四边形是平行四边形,
四边形是菱形;
(2)解:连接,
在中,,
设,则,
,
,
,
,
四边形是菱形的面积,
,
解得:;
(3)解:如图3,当点与点重合时,的面积最大,作于,则,
由题意得:,设,则;
由勾股定理得:,
解得:;由(1)知:
,,
,
面积的最大值为1.3,
故答案为:1.3
26. 类比和转化是数学中重要的思想方法,阅读下面的材料,并解答问题:
从数学课本中我们已经学习了利用平行四边形的定义和三个定理来判断一个四边形是平行四边形.张老师所在的班级成立了数学兴趣小组,他们在张老师的指导下对平行四边形的判定进行进一步的研究.他们发现:平行四边形的判定都需要两个条件,4个已经被证明的判定方法外,还有很多由两个条件组成的关于平行四边形判定的命题,他们对这些命题展开了研究.
(1)数学爱好者小潘和小苗发现“两组对角分别相等的四边形是平行四边形”是一个真命题.请你完成证明.如图1,在四边形中,,求证:四边形是平行四边形.
(2)小振和小涵研究后发现命题:“如果四边形满足一组对边相等且一条对角线平分另一条对角线,那么这个四边形是平行四边形”是一个假命题.他们先画出四边形的一条边,一条对角线.请你利用无刻度直尺和圆规在图2中画出反例.(保留作图痕迹,不写作法)
(3)数学课代表小骆想到了一个命题:“一组对角相等,一条对角线平分另一条对角线”,需要分情况考虑.聪明的同学们,你们能把这个问题研究一下吗?请在答题卡上写上你的研究成果(要求有必要的图形和文字说明).
【答案】(1)证明见解析;
(2)见解析; (3)证明见解析.
【解析】
【分析】本题主要考查了平行四边形的性质,平行四边形的判定,基本作图,反证法,熟练掌握平行四边形的性质与基本作图的方法是解题的关键.
(1)利用四边形的内角和定理和平行四边形的
定义解答即可;
(2)利用线段垂直平分线的作法找到的中点,连接并延长至点,使,得到平行四边形,再利用同圆的半径相等的性质得到点,则四边形可得;
(3)利用分类讨论的思想方法分两种情况推论解答:①已知,且,画出符合条件的反例即可;②已知,且,利用反证法解答即可.
【小问1详解】
证明:∵,
∴,
∴,
∴四边形为平行四边形.
【小问2详解】
作出线段的中点,连接并延长至点,以点为圆心,连接,
如图,
四边形即为所求,理由:
∵,
∴四边形为平行四边形,
∴,
由作法可知:,
∴
∴四边形中,,但四边形不是平行四边形.
【小问3详解】
解:分两种情况:①已知,且,
\
四边形满足一组对角相等,一条对角线平分另一条对角线;
②已知,且,
反证法:假设四边形不是平行四边形,则,
故可以在射线上取和不重合的点,使得,
∵,
∴四边形是平行四边形,
∴,
∵,
∴,
∴和重合,
这与点与点不重合矛盾,
∴假设不成立,
∴四边形是平行四边形.证法1:∵是的中位线,
∴_______.
∵是的中线,,
∴_______,
∴.
江苏省南京市致远初级中学2023-2024学年八年级下学期期中数学试题(原卷版+解析版): 这是一份江苏省南京市致远初级中学2023-2024学年八年级下学期期中数学试题(原卷版+解析版),文件包含江苏省南京市致远初级中学2023-2024学年八年级下学期期中数学试题原卷版docx、江苏省南京市致远初级中学2023-2024学年八年级下学期期中数学试题解析版docx等2份试卷配套教学资源,其中试卷共30页, 欢迎下载使用。
江苏省南京市南京师范大学附属中学新城初级中学2023-2024学年七年级下学期期中考试数学试卷: 这是一份江苏省南京市南京师范大学附属中学新城初级中学2023-2024学年七年级下学期期中考试数学试卷,共4页。
江苏省南京市南京师范大学附属中学新城初级中学2023-2024学年七年级下学期期中考试数学试卷: 这是一份江苏省南京市南京师范大学附属中学新城初级中学2023-2024学年七年级下学期期中考试数学试卷,共4页。












