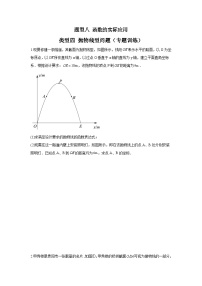
题型八 函数的实际应用 类型四 抛物线型问题16题(专题训练)-中考数学二轮复习满分冲刺题型突破(全国通用)
展开(1)求抛物线的函数表达式,并通过计算判断球能否射进球门(忽略其他因素).
(2)对本次训练进行分析,若射门路线的形状、最大高度均保持不变,则当时他应该带球向正后方移动多少米射门,才能让足球经过点O正上方2.25m处?
【答案】(1),球不能射进球门;(2)当时他应该带球向正后方移动1米射门
【分析】(1)根据建立的平面直角三角坐标系设抛物线解析式为顶点式,代入A点坐标求出a的值即可得到函数表达式,再把代入函数解析式,求出函数值,与球门高度比较即可得到结论;
(2)根据二次函数平移的规律,设出平移后的解析式,然后将点代入即可求解.
【详解】(1)解:由题意得:抛物线的顶点坐标为,
设抛物线解析式为,
把点代入,得,
解得,
∴抛物线的函数表达式为,
当时,,
∴球不能射进球门;
(2)设小明带球向正后方移动米,则移动后的抛物线为,
把点代入得,
解得(舍去),,
∴当时他应该带球向正后方移动1米射门.
【点睛】此题考查了二次函数的应用,待定系数法求函数解析式、二次函数图象的平移等知识,读懂题意,熟练掌握待定系数法是解题的关键.
2.现要修建一条隧道,其截面为抛物线型,如图所示,线段表示水平的路面,以O为坐标原点,以所在直线为x轴,以过点O垂直于x轴的直线为y轴,建立平面直角坐标系.根据设计要求:,该抛物线的顶点P到的距离为.
(1)求满足设计要求的抛物线的函数表达式;
(2)现需在这一隧道内壁上安装照明灯,如图所示,即在该抛物线上的点A、B处分别安装照明灯.已知点A、B到的距离均为,求点A、B的坐标.
【答案】(1)
(2)
【分析】(1)根据题意,设抛物线的函数表达式为,再代入(0,0),求出a的值即可;
(2)根据题意知,A,B两点的纵坐标为6,代入函数解析式可求出两点的横坐标,从而 可解决问题.
(1)
依题意,顶点,
设抛物线的函数表达式为,
将代入,得.解之,得.
∴抛物线的函数表达式为.
(2)
令,得.
解之,得.
∴.
【点睛】本题考查了运用待定系数法求二次函数的解析式的运用,由函数值求自变量的值的运用,解答时求出二次函数的解析式是关键.
3.(2023·湖北武汉·统考中考真题)某课外科技活动小组研制了一种航模飞机.通过实验,收集了飞机相对于出发点的飞行水平距离(单位:)以、飞行高度(单位:)随飞行时间(单位:)变化的数据如下表.
探究发现:与,与之间的数量关系可以用我们已学过的函数来描述.直接写出关于的函数解析式和关于的函数解析式(不要求写出自变量的取值范围).
问题解决:如图,活动小组在水平安全线上处设置一个高度可以变化的发射平台试飞该航模飞机.根据上面的探究发现解决下列问题.
(1)若发射平台相对于安全线的高度为0m,求飞机落到安全线时飞行的水平距离;
(2)在安全线上设置回收区域.若飞机落到内(不包括端点),求发射平台相对于安全线的高度的变化范围.
【答案】探索发现:;问题解决:(1);(2)大于且小于
【分析】探究发现:根据待定系数法求解即可;
问题解决:(1)令二次函数代入函数解析式即可求解;
(2)设发射平台相对于安全线的高度为,则飞机相对于安全线的飞行高度.结合,即可求解.
【详解】探究发现:x与t是一次函数关系,y与t是二次函数关系,
设,,
由题意得:,,
解得:,
∴.
问题解决(1) 解:依题总,得.
解得,(舍),,
当时,.
答:飞机落到安全线时飞行的水平距离为.
(2)解:设发射平台相对于安全线的高度为,飞机相对于安全线的飞行高度.
,
,
,
在中,
当时,;
当时,.
.
答:发射平台相对于安全线的高度的变化范围是大于且小于.
【点睛】本题考查了一次函数与二次函数的应用,利用待定系数法求函数的解析式,关键是把实际问题分析转变成数学模型.
4.甲秀楼是贵阳市一张靓丽的名片.如图①,甲秀楼的桥拱截面可视为抛物线的一部分,在某一时刻,桥拱内的水面宽,桥拱顶点到水面的距离是.
(1)按如图②所示建立平面直角坐标系,求桥拱部分抛物线的函数表达式;
(2)一只宽为的打捞船径直向桥驶来,当船驶到桥拱下方且距点时,桥下水位刚好在处.有一名身高的工人站立在打捞船正中间清理垃圾,他的头顶是否会触碰到桥拱,请说明理由(假设船底与水面齐平);
(3)如图③,桥拱所在的函数图象是抛物线,该抛物线在轴下方部分与桥拱在平静水面中的倒影组成一个新函数图象.将新函数图象向右平移个单位长度,平移后的函数图象在时,的值随值的增大而减小,结合函数图象,求的取值范围.
【答案】(1)y=x2+2x(0≤x≤8);(2)他的头顶不会触碰到桥拱,理由见详解;(3)5≤m≤8
【分析】
(1)设二次函数的解析式为:y=a(x-8)x,根据待定系数法,即可求解;
(2)把:x =1,代入y=x2+2x,得到对应的y值,进而即可得到结论;
(3)根据题意得到新函数解析式,并画出函数图像,进而即可得到m的范围.
【详解】
(1)根据题意得:A(8,0),B(4,4),
设二次函数的解析式为:y=a(x-8)x,
把(4,4)代入上式,得:4=a×(4-8)×4,解得:,
∴二次函数的解析式为:y= (x-8)x=x2+2x(0≤x≤8);
(2)由题意得:x=0.4+1.2÷2=1,代入y=x2+2x,得y=×12+2×1=>1.68,
答:他的头顶不会触碰到桥拱;
(3)由题意得:当0≤x≤8时,新函数表达式为:y=x2-2x,
当x<0或x>8时,新函数表达式为:y=-x2+2x,
∴新函数表达式为:,
∵将新函数图象向右平移个单位长度,
∴(m,0),(m+8,0),(m+4,-4),如图所示,
根据图像可知:当m+4≥9且m≤8时,即:5≤m≤8时,平移后的函数图象在时,的值随值的增大而减小.
【点睛】
本题主要考查二次函数的实际应用,掌握二次函数的待定系数法,二次函数的图像和性质,二次函数图像平移和轴对称变换规律,是解题的关键.
5.(2023·河北·统考中考真题)嘉嘉和淇淇在玩沙包游戏.某同学借此情境编制了一道数学题,请解答这道题.
如图,在平面直角坐标系中,一个单位长度代表1m长.嘉嘉在点处将沙包(看成点)抛出,并运动路线为抛物线的一部分,淇淇恰在点处接住,然后跳起将沙包回传,其运动路线为抛物线的一部分.
(1)写出的最高点坐标,并求a,c的值;
(2)若嘉嘉在x轴上方的高度上,且到点A水平距离不超过的范围内可以接到沙包,求符合条件的n的整数值.
【答案】(1)的最高点坐标为,,;(2)符合条件的n的整数值为4和5
【分析】(1)利用顶点式即可得到最高点坐标;点在抛物线上,利用待定系数法即可求得a的值;令,即可求得c的值;
(2)求得点A的坐标范围为,求得n的取值范围,即可求解.
【详解】(1)解:∵抛物线,
∴的最高点坐标为,
∵点在抛物线上,
∴,解得:,
∴抛物线的解析式为,令,则;
(2)解:∵到点A水平距离不超过的范围内可以接到沙包,
∴点A的坐标范围为,
当经过时,,
解得;
当经过时,,
解得;
∴
∴符合条件的n的整数值为4和5.
【点睛】本题考查了二次函数的应用,联系实际,读懂题意,熟练掌握二次函数图象上点的坐标特征是解题的关键.
6.2022年北京冬奥会即将召开,激起了人们对冰雪运动的极大热情.如图是某跳台滑雪训练场的横截面示意图,取某一位置的水平线为轴,过跳台终点作水平线的垂线为轴,建立平面直角坐标系.图中的抛物线近似表示滑雪场地上的一座小山坡,某运动员从点正上方米处的点滑出,滑出后沿一段抛物线运动.
(1)当运动员运动到离处的水平距离为米时,离水平线的高度为米,求抛物线的函数解析式(不要求写出自变量的取值范围);
(2)在(1)的条件下,当运动员运动水平线的水平距离为多少米时,运动员与小山坡的竖直距离为米?
(3)当运动员运动到坡顶正上方,且与坡顶距离超过米时,求的取值范围.
【答案】(1);(2)12米;(3).
【分析】
(1)根据题意可知:点A(0,4)点B(4,8),利用待定系数法代入抛物线即可求解;
(2)高度差为1米可得可得方程,由此即可求解;
(3)由抛物线可知坡顶坐标为 ,此时即当时,运动员运动到坡顶正上方,若与坡顶距离超过米,即,由此即可求出b的取值范围.
【详解】
解:(1)根据题意可知:点A(0,4),点B(4,8)代入抛物线得,
,
解得:,
∴抛物线的函数解析式;
(2)∵运动员与小山坡的竖直距离为米,
∴,
解得:(不合题意,舍去), ,
故当运动员运动水平线的水平距离为12米时,运动员与小山坡的竖直距离为米;
(3)∵点A(0,4),
∴抛物线,
∵抛物线,
∴坡顶坐标为 ,
∵当运动员运动到坡顶正上方,且与坡顶距离超过米时,
∴,
解得:.
【点睛】
本题属二次函数应用中的难题.解决函数应用问题的一般步骤为:(1)审题:弄清题意,分清条件和结论,理清数量关系;(2)建模:将文字语言转化为数学语言,利用数学知识建立相应的数学模型;(3)求模:求解数学模型,得到数学结论;(4) 还原:将用数学方法得到的结论还原为实际问题.
7.(2023·河南·统考中考真题)小林同学不仅是一名羽毛球运动爱好者,还喜欢运用数学知识对羽毛球比赛进行技术分析,下面是他对击球线路的分析.
如图,在平面直角坐标系中,点A,C在x轴上,球网与y轴的水平距离,,击球点P在y轴上.若选择扣球,羽毛球的飞行高度与水平距离近似满足一次函数关系;若选择吊球,羽毛球的飞行高度与水平距离近似满足二次函数关系.
(1)求点P的坐标和a的值.
(2)小林分析发现,上面两种击球方式均能使球过网.要使球的落地点到C点的距离更近,请通过计算判断应选择哪种击球方式.
【答案】(1),;(2)选择吊球,使球的落地点到C点的距离更近
【分析】(1)在一次函数上,令,可求得,再代入即可求得的值;
(2)由题意可知,令,分别求得,,即可求得落地点到点的距离,即可判断谁更近.
【详解】(1)解:在一次函数,
令时,,
∴,
将代入中,可得:,
解得:;
(2)∵,,
∴,
选择扣球,则令,即:,解得:,
即:落地点距离点距离为,
∴落地点到C点的距离为,
选择吊球,则令,即:,解得:(负值舍去),
即:落地点距离点距离为,
∴落地点到C点的距离为,
∵,
∴选择吊球,使球的落地点到C点的距离更近.
【点睛】本题考查二次函数与一次函数的应用,理解题意,求得函数解析式是解决问题的关键.
8.如图是一块铁皮余料,将其放置在平面直角坐标系中,底部边缘在轴上,且dm,外轮廓线是抛物线的一部分,对称轴为轴,高度dm.现计划将此余料进行切割:
(1)若切割成正方形,要求一边在底部边缘上且面积最大,求此正方形的面积;
(2)若切割成矩形,要求一边在底部边缘上且周长最大,求此矩形的周长;
(3)若切割成圆,判断能否切得半径为dm的圆,请说明理由.
【答案】(1) ;
(2)20dm;
(3)能切得半径为3dm的圆.
【分析】(1)先把二次函数解析式求出来,设正方形的边长为2m,表示在二次函数上点的坐标,代入即可得到关于m的方程进行求解;
(2)如详解2中图所示,设矩形落在AB上的边DE=2n,利用函数解析式求解F点坐标,进而表示出矩形的周长求最大值即可;
(3)为了保证尽可能截取圆,应保证圆心H坐标为(0,3),表示出圆心H到二次函数上个点之间的距离与半径3进行比较即可.
(1)
由题目可知A(-4,0),B(4,0),C(0,8)
设二次函数解析式为y=ax²+bx+c,
∵对称轴为y轴,
∴b=0,将A、C代入得,a=,c=8
则二次函数解析式为,
如下图所示,正方形MNPQ即为符合题意得正方形,设其边长为2m,
则P点坐标可以表示为(m,2m)
代入二次函数解析式得,
,解得(舍去),
∴2m=,
则正方形的面积为;
(2)
如下如所示矩形DEFG,设DE=2n,则E(n,0)
将x=n代入二次函数解析式,得
,
则EF=,
矩形DEFG的周长为:2(DE+EF)=2(2n+)=,
当n=2时,矩形的周长最大,最大周长为20dm;
(3)
如下图所示,为了保证尽可能截取圆,应保证圆心H坐标为(0,3),
则圆心H到二次函数上个点之间的距离为,
∴能切得半径为3dm的圆.
【点睛】本题考查了二次函数与几何结合,熟练掌握各图形的性质,能灵活运用坐标与线段长度之间的转换是解题的关键.
9.(2023·内蒙古赤峰·统考中考真题)乒乓球被誉为中国国球.2023年的世界乒乓球标赛中,中国队包揽了五个项目的冠军,成绩的取得与平时的刻苦训练和精准的技术分析是分不开的.如图,是乒乓球台的截面示意图,一位运动员从球台边缘正上方以击球高度为的高度,将乒乓球向正前方击打到对面球台,乒乓球的运行路线近似是抛物线的一部分.
乒乓球到球台的竖直高度记为(单位:),乒乓球运行的水平距离记为(单位:).测得如下数据:
(1)在平面直角坐标系中,描出表格中各组数值所对应的点,并画出表示乒乓球运行轨迹形状的大致图象;
(2)①当乒乓球到达最高点时,与球台之间的距离是__________,当乒乓球落在对面球台上时,到起始点的水平距离是__________;
②求满足条件的抛物线解析式;
(3)技术分析:如果只上下调整击球高度,乒乓球的运行轨迹形状不变,那么为了确保乒乓球既能过网,又能落在对面球台上,需要计算出的取值范围,以利于有针对性的训练.如图②.乒乓球台长为274,球网高为15.25.现在已经计算出乒乓球恰好过网的击球离度的值约为1.27.请你计算出乒乓球恰好落在对面球台边缘点B处时,击球高度的值(乒乓球大小忽略不计).
【答案】(1)见解析;(2)①;;②;(3)乒乓球恰好落在对面球台边缘点B处时,击球高度的值为
【分析】(1)根据描点法画出函数图象即可求解;
(2)①根据二次函数图象的对称性求得对称轴以及顶点,根据表格数据,可得当时,;
②待定系数法求解析式即可求解;
(3)根据题意,设平移后的抛物线的解析式为,根据题意当时,,代入进行计算即可求解.
【详解】(1)解:如图所示,
(2)①观察表格数据,可知当和时,函数值相等,则对称轴为直线,顶点坐标为,
又抛物线开口向下,可得最高点时,与球台之间的距离是,
当时,,
∴乒乓球落在对面球台上时,到起始点的水平距离是;
故答案为:;.
②设抛物线解析式为,将代入得,
,
解得:,
∴抛物线解析式为;
(3)∵当时,抛物线的解析式为,
设乒乓球恰好落在对面球台边缘点B处时,击球高度的值为,则平移距离为,
∴平移后的抛物线的解析式为,
依题意,当时,,
即,
解得:.
答:乒乓球恰好落在对面球台边缘点B处时,击球高度的值为.
【点睛】本题考查了二次函数的应用,画二次函数图象,二次函数图象的平移,熟练掌握二次函数图象的性质是解题的关键.
10.跳台滑雪运动可分为助滑、起跳、飞行和落地四个阶段,运动员起跳后飞行的路线是抛物线的一部分(如图中实线部分所示),落地点在着陆坡(如图中虚线部分所示)上,着陆坡上的基准点K为飞行距离计分的参照点,落地点超过K点越远,飞行距离分越高.2022年北京冬奥会跳台滑雪标准台的起跳台的高度为,基准点K到起跳台的水平距离为,高度为(h为定值).设运动员从起跳点A起跳后的高度与水平距离之间的函数关系为.
(1)c的值为__________;
(2)①若运动员落地点恰好到达K点,且此时,求基准点K的高度h;
②若时,运动员落地点要超过K点,则b的取值范围为__________;
(3)若运动员飞行的水平距离为时,恰好达到最大高度,试判断他的落地点能否超过K点,并说明理由.
【答案】(1)66
(2)①基准点K的高度h为21m;②b>;
(3)他的落地点能超过K点,理由见解析.
【分析】(1)根据起跳台的高度OA为66m,即可得c=66;
(2)①由a=﹣ ,b=,知y=﹣x2+x+66,根据基准点K到起跳台的水平距离为75m,即得基准点K的高度h为21m;
②运动员落地点要超过K点,即是x=75时,y>21,故﹣×752+75b+66>21,即可解得答案;
(3)运动员飞行的水平距离为25m时,恰好达到最大高度76m,即是抛物线的顶点为(25,76),设抛物线解析式为y=a(x﹣25)2+76,可得抛物线解析式为y=﹣(x﹣25)2+76,当x=75时,y=36,从而可知他的落地点能超过K点.
(1)
解:∵起跳台的高度OA为66m,
∴A(0,66),
把A(0,66)代入y=ax2+bx+c得:
c=66,
故答案为:66;
(2)
解:①∵a=﹣,b=,
∴y=﹣x2+x+66,
∵基准点K到起跳台的水平距离为75m,
∴y=﹣×752+×75+66=21,
∴基准点K的高度h为21m;
②∵a=﹣,
∴y=﹣x2+bx+66,
∵运动员落地点要超过K点,
∴当x=75时,y>21,
即﹣×752+75b+66>21,
解得b>,
故答案为:b>;
(3)
解:他的落地点能超过K点,理由如下:
∵运动员飞行的水平距离为25m时,恰好达到最大高度76m,
∴抛物线的顶点为(25,76),
设抛物线解析式为y=a(x﹣25)2+76,
把(0,66)代入得:
66=a(0﹣25)2+76,
解得a=﹣,
∴抛物线解析式为y=﹣(x﹣25)2+76,
当x=75时,y=﹣×(75﹣25)2+76=36,
∵36>21,
∴他的落地点能超过K点.
【点睛】本题考查二次函数的应用,解题的关键是读懂题意,能根据题意把实际问题转化为数学问题.
11.(2023·广东深圳·统考中考真题)蔬菜大棚是一种具有出色的保温性能的框架覆膜结构,它出现使得人们可以吃到反季节蔬菜.一般蔬菜大棚使用竹结构或者钢结构的骨架,上面覆上一层或多层保温塑料膜,这样就形成了一个温室空间.如图,某个温室大棚的横截面可以看作矩形和抛物线构成,其中,,取中点O,过点O作线段的垂直平分线交抛物线于点E,若以O点为原点,所在直线为x轴,为y轴建立如图所示平面直角坐标系.
请回答下列问题:
(1)如图,抛物线的顶点,求抛物线的解析式;
(2)如图,为了保证蔬菜大棚的通风性,该大棚要安装两个正方形孔的排气装置,,若,求两个正方形装置的间距的长;
(3)如图,在某一时刻,太阳光线透过A点恰好照射到C点,此时大棚截面的阴影为,求的长.
【答案】(1);(2);(3)
【分析】(1)根据顶点坐标,设函数解析式为,求出点坐标,待定系数法求出函数解析式即可;
(2)求出时对应的自变量的值,得到的长,再减去两个正方形的边长即可得解;
(3)求出直线的解析式,进而设出过点的光线解析式为,利用光线与抛物线相切,求出的值,进而求出点坐标,即可得出的长.
【详解】(1)解:∵抛物线的顶点,
设抛物线的解析式为,
∵四边形为矩形,为的中垂线,
∴,,
∵,
∴点,代入,得:
,
∴,
∴抛物线的解析式为;
(2)∵四边形,四边形均为正方形,,
∴,
延长交于点,延长交于点,则四边形,四边形均为矩形,
∴,
∴,
∵,当时,,解得:,
∴,,
∴,
∴;
(3)∵,垂直平分,
∴,
∴,
设直线的解析式为,
则:,解得:,
∴,
∵太阳光为平行光,
设过点平行于的光线的解析式为,
由题意,得:与抛物线相切,
联立,整理得:,
则:,解得:;
∴,当时,,
∴,
∵,
∴.
【点睛】本题考查二次函数的实际应用.读懂题意,正确的求出二次函数解析式,利用数形结合的思想,进行求解,是解题的关键.
12.根据以下素材,探索完成任务.
如何设计拱桥景观灯的悬挂方案?
素材1
图1中有一座拱桥,图2是其抛物线形桥拱的示意图,某时测得水面宽,拱顶离水面.据调查,该河段水位在此基础上再涨达到最高.
素材2
为迎佳节,拟在图1桥洞前面的桥拱上悬挂长的灯笼,如图3.为了安全,灯笼底部距离水面不小于;为了实效,相邻两盏灯笼悬挂点的水平间距均为;为了美观,要求在符合条件处都挂上灯笼,且挂满后成轴对称分布.
问题解决
任务1
确定桥拱形状
在图2中建立合适的直角坐标系,求抛物线的函数表达式.
任务2
探究悬挂范围
在你所建立的坐标系中,仅在安全的条件下,确定悬挂点的纵坐标的最小值和横坐标的取值范围.
任务3
拟定设计方案
给出一种符合所有悬挂条件的灯笼数量,并根据你所建立的坐标系,求出最左边一盏灯笼悬挂点的横坐标.
【答案】任务一:见解析,;任务二:悬挂点的纵坐标的最小值是;;任务三:两种方案,见解析
【分析】任务一:根据题意,以拱顶为原点,建立如图1所示的直角坐标系,待定系数法求解析式即可求解;
任务二:根据题意,求得悬挂点的纵坐标,进而代入函数解析式即可求得横坐标的范围;
任务三:有两种设计方案,分情况讨论,方案一:如图2(坐标系的横轴,图3同),从顶点处开始悬挂灯笼;方案二:如图3,从对称轴两侧开始悬挂灯笼,正中间两盏与对称轴的距离均为,根据题意求得任意一种方案即可求解.
【详解】任务一:以拱顶为原点,建立如图1所示的直角坐标系,
则顶点为,且经过点.
设该抛物线函数表达式为,
则,
∴,
∴该抛物线的函数表达式是.
任务二:∵水位再上涨达到最高,灯笼底部距离水面至少,灯笼长,
∴悬挂点的纵坐标,
∴悬挂点的纵坐标的最小值是.
当时,,解得或,
∴悬挂点的横坐标的取值范围是.
任务三:有两种设计方案
方案一:如图2(坐标系的横轴,图3同),从顶点处开始悬挂灯笼.
∵,相邻两灯笼悬挂点的水平间距均为,
∴若顶点一侧挂4盏灯笼,则,
若顶点一侧挂3盏灯笼,则,
∴顶点一侧最多可挂3盏灯笼.
∵挂满灯笼后成轴对称分布,
∴共可挂7盏灯笼.
∴最左边一盏灯笼悬挂点的横坐标是.
方案二:如图3,从对称轴两侧开始悬挂灯笼,正中间两盏与对称轴的距离均为,
∵若顶点一侧挂5盏灯笼,则,
若顶点一侧挂4盏灯笼,则,
∴顶点一侧最多可挂4盏灯笼.
∵挂满灯笼后成轴对称分布,
∴共可挂8盏灯笼.
∴最左边一盏灯笼悬挂点的横坐标是.
【点睛】本题考查了二次函数的应用,根据题意建立坐标系,掌握二次函数的性质是解题的关键.
13.如今我国的大棚(如图1)种植技术已十分成熟.小明家的菜地上有一个长为16米的蔬菜大棚,其横截面顶部为抛物线型,大棚的一端固定在离地面高1米的墙体处,另一端固定在离地面高2米的墙体处,现对其横截面建立如图2所示的平面直角坐标系.已知大棚上某处离地面的高度(米)与其离墙体的水平距离(米)之间的关系满足,现测得,两墙体之间的水平距离为6米.
图2
(1)直接写出,的值;
(2)求大棚的最高处到地面的距离;
(3)小明的爸爸欲在大棚内种植黄瓜,需搭建高为米的竹竿支架若干,已知大棚内可以搭建支架的土地平均每平方米需要4根竹竿,则共需要准备多少根竹竿?
【答案】(1),;(2)米;(3)352
【分析】
(1)根据题意,可直接写出点A点B坐标,代入,求出b、c即可;
(2)根据(1)中函数解析式直接求顶点坐标即可;
(3根据,先求得大棚内可以搭建支架的土地的宽,再求得需搭建支架的面积,最后根据每平方米需要4根竹竿计算即可.
【详解】
解:(1)由题意知点A坐标为,点B坐标为,
将A、B坐标代入得:
解得:,
故,;
(2)由,
可得当时,有最大值,
即大棚最高处到地面的距离为米;
(3)由,解得,,
又因为,
可知大棚内可以搭建支架的土地的宽为(米),
又大棚的长为16米,故需要搭建支架部分的土地面积为(平方米)
共需要(根)竹竿.
【点睛】
本题主要考查根据待定系数法求函数解析式,根据函数解析式求顶点坐标,以及根据函数值确定自变量取值范围,掌握此题的关键是熟练掌握二次函数图像的性质.
14.如图1是一座抛物线型拱桥侧面示意图.水面宽AB与桥长CD均为24m,在距离D点6米的E处,测得桥面到桥拱的距离EF为1.5m,以桥拱顶点O为原点,桥面为x轴建立平面直角坐标系.
(1)求桥拱项部O离水面的距离.
(2)如图2,桥面上方有3根高度均为4m的支柱CG,OH,DI,过相邻两根支柱顶端的钢缆呈形状相同的抛物线,其最低点到桥面距离为1m.
①求出其中一条钢缆抛物线的函数表达式.
②为庆祝节日,在钢缆和桥拱之间竖直装饰若干条彩带,求彩带长度的最小值.
【答案】(1)6m;(2)①;②2m
【分析】
(1)设,由题意得,求出抛物线图像解析式,求当x=12或x=-12时y1的值即可;
(2)①由题意得右边的抛物线顶点为,设,将点H代入求值即可;
②设彩带长度为h,则,代入求值即可.
【详解】
解(1)设,由题意得,
,
,
,
当时,,
桥拱顶部离水面高度为6m.
(2)①由题意得右边的抛物线顶点为,
设,
,
,
,
,
(左边抛物线表达式:)
②设彩带长度为h,
则,
当时,,
答:彩带长度的最小值是2m .
【点睛】
本题主要考查待定系数法求二次函数的解析式,以及二次函数最值得求解方法,结合题意根据数形结合的思想设出二次函数的顶点式方程是解题的关键.
15.(2021·浙江金华市·中考真题)某游乐场的圆形喷水池中心O有一雕塑OA,从A点向四周喷水,喷出的水柱为抛物线,且形状相同.如图,以水平方向为x轴,点O为原点建立直角坐标系,点A在y轴上,x轴上的点C,D为水柱的落水点,水柱所在抛物线第一象限部分的函数表达式为.
(1)求雕塑高OA.
(2)求落水点C,D之间的距离.
(3)若需要在OD上的点E处竖立雕塑EF,,.问:顶部F是否会碰到水柱?请通过计算说明.
【答案】(1);(2)22米;(3)不会
【分析】
(1)求雕塑高,直接令,代入求解可得;
(2)可先求出的距离,再根据对称性求的长;
(3)利用,计算出的函数值,再与的长进行比较可得结论.
【详解】
解:(1)由题意得,A点在图象上.
当时,
.
(2)由题意得,D点在图象上.
令,得.
解得:(不合题意,舍去).
(3)当时,,
,
∴不会碰到水柱.
【点睛】
本题考查了二次函数的图像与性质及图像关于轴对称问题,解题的关键是:掌握二次函数的图像与性质.
16.(2021·山东临沂市·中考真题)公路上正在行驶的甲车,发现前方20m处沿同一方向行驶的乙车后,开始减速,减速后甲车行驶的路程s(单位:m)、速度v(单位:m/s)与时间t(单位:s) 的关系分别可以用二次函数和一次函数表示,其图象如图所示.
(1)当甲车减速至9m/s时,它行驶的路程是多少?
(2)若乙车以10m/s的速度匀速行驶,两车何时相距最近,最近距离是多少?
【答案】(1)87.5m;(2)6秒时两车相距最近,最近距离是2米
【分析】
(1)根据图像分别求出一次函数和二次函数解析式,令v=9求出t,代入求出s即可;
(2)分析得出当v=10m/s时,两车之间距离最小,代入计算即可.
【详解】
解:(1)由图可知:二次函数图像经过原点,
设二次函数表达式为,一次函数表达式为,
∵一次函数经过(0,16),(8,8),
则,解得:,
∴一次函数表达式为,
令v=9,则t=7,
∴当t=7时,速度为9m/s,
∵二次函数经过(2,30),(4,56),
则,解得:,
∴二次函数表达式为,
令t=7,则s==87.5,
∴当甲车减速至9m/s时,它行驶的路程是87.5m;
(2)∵当t=0时,甲车的速度为16m/s,
∴当10<v<16时,两车之间的距离逐渐变小,
当0<v<10时,两车之间的距离逐渐变大,
∴当v=10m/s时,两车之间距离最小,
将v=10代入中,得t=6,
将t=6代入中,得,
此时两车之间的距离为:10×6+20-78=2m,
∴6秒时两车相距最近,最近距离是2米.
【点睛】
本题考查了二次函数与一次函数的实际应用,理解题意,读懂函数图像,求出表达式是解题的基本前提.
飞行时间
0
2
4
6
8
…
飞行水平距离
0
10
20
30
40
…
飞行高度
0
22
40
54
64
…
水平距离x/
竖直高度y/
题型七 函数的基本性质 类型二反比例函数49题(专题训练)-中考数学二轮复习满分冲刺题型突破(全国通用): 这是一份题型七 函数的基本性质 类型二反比例函数49题(专题训练)-中考数学二轮复习满分冲刺题型突破(全国通用),文件包含题型七函数的基本性质类型二反比例函数49题专题训练原卷版docx、题型七函数的基本性质类型二反比例函数49题专题训练解析版docx等2份试卷配套教学资源,其中试卷共70页, 欢迎下载使用。
题型七 函数的基本性质 类型三二次函数45题(专题训练)-中考数学二轮复习满分冲刺题型突破(全国通用): 这是一份题型七 函数的基本性质 类型三二次函数45题(专题训练)-中考数学二轮复习满分冲刺题型突破(全国通用),文件包含题型七函数的基本性质类型三二次函数45题专题训练原卷版docx、题型七函数的基本性质类型三二次函数45题专题训练解析版docx等2份试卷配套教学资源,其中试卷共64页, 欢迎下载使用。
题型三 方程应用 类型二分式方程35题(专题训练)-中考数学二轮复习满分冲刺题型突破(全国通用): 这是一份题型三 方程应用 类型二分式方程35题(专题训练)-中考数学二轮复习满分冲刺题型突破(全国通用),文件包含题型三方程应用类型二分式方程35题专题训练原卷版docx、题型三方程应用类型二分式方程35题专题训练解析版docx等2份试卷配套教学资源,其中试卷共29页, 欢迎下载使用。