2024届云南省高三下学期3+3+3高考备考诊断性联考（二）数学试题

这是一份2024届云南省高三下学期3+3+3高考备考诊断性联考（二）数学试题，文件包含2024届”3+3+3“高考备考诊断性联考卷二数学试题pdf、2024届“3+3+3”高考备考诊断性联考卷二数学云南版-答案docx等2份试卷配套教学资源，其中试卷共16页， 欢迎下载使用。


一、选择题（本大题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的）
【解析】
1．，故，故选B．
2．掷两颗均匀的骰子的所有基本事件有种，点数之和小于5的有6种，所以所求概率为，故选D．
3．，故选A．
4．当时，，所以在上单调递增；又有为上的偶函数，所以在上单调递减．又有所以而又且所以，所以，故选C．
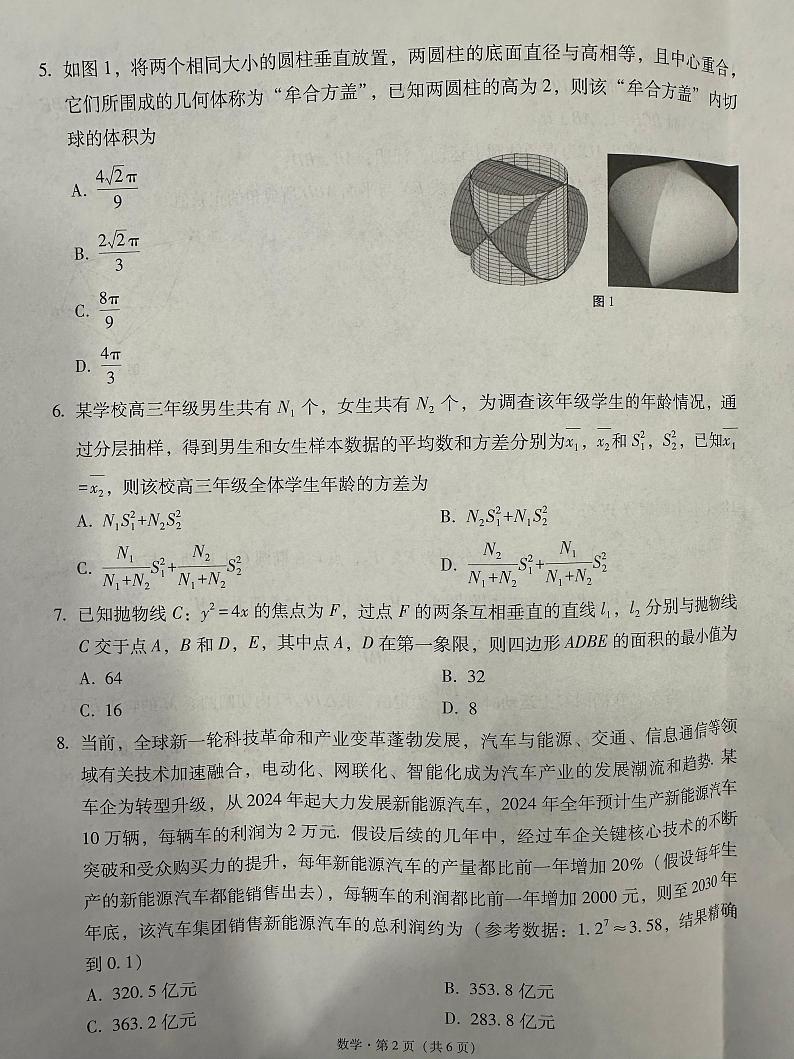
图1
5．如图1，将两个互相垂直的圆柱放到棱长为2的正方体内，则正方体的内切球与这两个圆柱的侧面和底面都相切，又因为牟合方盖上下两个顶点和侧面的四个曲面刚好与正方体的侧面相切，故正方体的内切球内切于牟合方盖，所以，正方体内切球即为牟合方盖的内切球，其半径为1，体积为，故选D．
6．学校高三年级男生共有个，所占比例为，女生个，所占比例为故该校高三年级全体学生的年龄方差为：当时，，故选C．
7．由题意得，设直线，与联立，得，设，故，则
，同理得：，∴
当且仅当时，等号成立，故选B．
8．设第n年每辆车的利润为万元，则每辆车的利润是以2为首项，为公差的等差数列，所以，设第n年新能源汽车的销量为辆，则该汽车的销量是以100000为首项，为公比的等比数列，所以，设该车企销售新能源汽车的总利润为S，∴
∴ ①，
②，
①−②得：
所以万元，即亿元，故选B．
二、选择题（本大题共3小题，每小题6分，共18分．在每小题给出的选项中，有多项是符合题目要求的．全部选对的得6分，部分选对的得部分分，有选错的得0分）
【解析】
9．由题意得：，所以，，即，又，所以，故．当时，，由余弦函数的图象知：在上是单调递减，故A正确；当时，，由余弦函数的图象知：有两个极值点，故B正确；当时，，不是余弦函数的对称轴； 故C不正确；由得，从而得：或，所以函数在点处的切线斜率为，切线方程为：即故D正确，故选ABD．
图4
图3
图2
10．由题意可得，，将平面和平面沿直线展开，如图2，在中，，，，所以，则的最小值为，故A错；∵，平面，∴平面，即到平面的距离为定值，即三棱锥的高为定值，又∵为定值，所以为定值，故B正确；如图3，连接，取棱，，的中点分别为，取线段的中点为，连接，因为在平面内的投影为，，由三垂线定理可得，，连接，∵，，∴平面，∴在平面内的投影为，，由三垂线定理可得，，连接，则平面，∴点的轨迹为平行四边形，故C正确；，如图4，以为球心，为半径作球，则点的轨迹即为该球与直四棱柱各面截球所得的弧，在线段上取一点，使得，上取一点，使得，则，平面截球得，长度为，平面截球得，长度，∵平面，，∴平面截球得，长度为，同理可得，平面截球得，长度为，平面与球相切与点，则点的轨迹长度为，故D正确，故选BCD．
11．令，则，所以或，若，则当时，，这与矛盾，故，令，则，故．又的定义域为关于原点对称，所以是偶函数，故A正确；当时，，故，又当时，，所以，则，所以，故是以4为周期的周期函数，又由是偶函数可得：关于直线对称，若关于点对称，则，与矛盾，故B错误；若，则是周期为4的周期数列，又，而，所以的前2024项和为0，故C正确；令，则，即，可设，由可得，故时成立，经检验可知原条件均成立，此时有，故D正确，故选ACD．
三、填空题（本大题共3小题，每小题5分，共15分）
【解析】
12．由≥2得：≤3，所以≤3，因为且，所以．
13．5个人住4个房间，每个房间至少住1人，则有一个房间住两人，其他房间住一人，所以有（种）．
14．设∵故，
∴则又都在椭圆上，故，且，两式相减得：，即①，同理可得：②，②−①得：，所以．
四、解答题（本大题共5小题，共77分．解答应写出文字说明，证明过程或演算步骤）
15．（本小题满分13分）
解：（1）由
得：
即：……………………………………………………………（3分）
∴ 即：
又∵，∴ ……………………………………………………………（5分）
（2）由（1）知：∴
在中，
在中，………………………………………………………（7分）
又，代入得：．……………………………（9分）
由余弦定理得：，……………………………………（11分）
所以………………………………………………………（13分）
16．（本小题满分15分）
解：（1）∵，∴，
∴函数在的切线的方程为．………………………………………（2分）
∵，∴，令，得，……………………………（4分）
故而，所以．……………………………………………………（5分）
（2）由恒成立，等价于恒成立，
即：恒成立，
令，则 …………………………………………………（8分）
又∵，∴在上单调递增，
∴恒成立，即 …………………………………………………（11分）
令，所以，
则为上的增函数，上的减函数，
所以，所以的取值范围是：………………………………（15分）
17．（本小题满分15分）
（1）证明：如图5，过点作的平行线，即为．
理由如下：
∵∥，，，
∴∥平面．
图5
又∵，且平面平面
∴∥．
又∵∴ ……………………………………………………………（4分）
又∵在以为直径的圆上运动，∴
又∵，∴平面，
∴．……………………………………………………………………………（6分）
（2）解：在中，，，∴，
故
由（1）知：，，
∴平面.
又∵，∴平面……………………………………………………（9分）
令，则即为直线与平面所成的角，…………………（11分）
∴，
在中，，………………………………（13分）
∴，
即直线与平面所成角的正弦值为……………………………………（15分）
18．（本小题满分17分）
解：（1）当点运动到椭圆的上顶点时，如图6，
则：．
图6
…………………………………………………（2分）
的内切圆圆即为的重心．
∴，，
则．………………………………………………………………………………（5分）
（2）当点在椭圆C上运动时，设，过点作椭圆左准线的垂线，垂足为，
则：
又∵，∴
同理可得：
延长交轴于点，设，
∵点是内切圆圆心，∴由角平分线性质得：，即：化简得：①， ……………………………………………………………………（7分）
设内切圆圆心，由
得：②，……………………………………………………………（8分）
联立①②得：，．
又∵在椭圆上，
∴即内切圆圆心的轨迹方程为：……………………………（10分）
（3）∵点与点关于轴对称，
∴设，
∴由三点共线可得：③，
由三点共线可得：④，
③×④得：
又∵在曲线上，
∴，即
∴ 点的轨迹方程Γ为：………………………………………………（13分）
当直线的斜率不存在时，直线的方程为：
此时直线与双曲线只有一个交点，不成立；
当直线的斜率存在时，设且
∵点在双曲线上，
∴两式子相减得：
∴
若点是线段AB的中点，则即
代入上式子得：则直线的斜率为：，
∴直线的方程为： 即
联立得：
故方程有解，
所以存在这样的直线：，使得点为线段AB的中点．
……………………………………………………………………………………（17分）
19．（本小题满分17分）
解：（1）记事件为一辆德国市场的电车性能很好，事件为一辆德国市场的车来自W公司．
由全概率公式知：
故： ……………………（6分）
（2）记事件表示小球开始位于第个格子，且最终停留在第10个格子，
事件表示小球向右走一格.
小球开始于第i格，此时的概率为，
则下一步小球向左或向右移动，当小球向右移动，即可理解为小球始于，当小球向左移动，即可理解为小球始于，
即 ……………………………………………………………………（9分）
由题知，
又，故，…………………………………………（11分）
所以是以为首项，3为公比的等比数列，
即：，
即：
…

故， …………………………………………（13分）
，………………………………………………（15分）
则，
故这名顾客获得代金券的概率为………………………………………………（17分）题号
1
2
3
4
5
6
7
8
答案
B
D
A
C
D
C
B
B
题号
9
10
11
答案
ABD
BCD
ACD
题号
12
13
14
答案
216