


安徽省示范高中皖北协作区2024届高三下学期3月联考数学试题(Word版附答案)
展开数 学
考生注意:
1. 答题前,考生务必将自己的姓名、考生号填写在试卷和答题卡上,并将考生号条形码粘贴在答题卡上的指定位置.
2. 回答选择题时,选出每小题答案后,用铅笔把答题卡对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其他答案标号.回答非选择题时,将答案写在答题卡上.写在本试卷上无效.
3. 考试结束后,将本试卷和答题卡一并交回.
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1 50833:uId:50833 . 已知集合A={x|y=},B={x|x>3或x<-3},则(RA)∪B=
A.[-3,-2]B.(-∞,-3)∪(-2,+∞)
C.[-2,3]D.(-∞,-2)∪(3,+∞)
2. 已知复数z=1+2i,则在复平面内对应的点的坐标为
A.(,)B.(,-)
C.(-,)D.(-,-)
3. 若a>0,b>0,则“≤2”是“a+b≤1”的
A.充分不必要条件B.必要不充分条件
C.充要条件D.既不充分也不必要条件
4. 已知在单调递增的等差数列{an}中,a3与a7的等差中项为8,且a2·a8=-17,则{an}的公差d=
A.5B.4C.3D.2
5. 科学家从由实际生活得出的大量统计数据中发现以1开头的数出现的频率较高,以1开头的数出现的频数约为总数的三成,并提出定律:在大量b进制随机数据中,以n开头的数出现的概率为Pb(n)=,如斐波那契数、阶乘数、素数等都比较符合该定律.后来常有数学爱好者用此定律来检验某些经济数据、选举数据等大数据的真实性.若(k∈N*,k>4),则k的值为
A 1068003:fId:1068003 .11B.15
C.19D.21
6. 已知tan(α-β)=,sin(α-β)=3cs(α+β),则tan α-tan β=
A.B.C.D.
7. 设P-ABCD与Q-ABCD为两个正四棱锥,正方形ABCD的边长为且∠PCQ=90°,点M在线段AC上,且3CM=AM,将异面直线PD,QM所成的角记为θ,则sin θ的最小值为
A.B.C.D.
8. 已知点M是直线l1:ax+y-2a=0和l2:x-ay+2=0(a∈R)的交点,A(-1,0),B(m,0),且点M满足|MA|=|MB|恒成立.若C(2,2),则2|MA|+|MC|的最小值为
A.B.2C.D.2
二、多项选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求,全部选对的得6分,部分选对的得部分分,有选错的得0分.
9. 已知样本数据x1,x2,x3,x4,x5(x1<0,x2,x3,x4,x5>0)的方差为s2,平均数>0,则
A.数据3x1-2,3x2-2,3x3-2,3x4-2,3x5-2的方差为9s2
B.数据3x1-2,3x2-2,3x3-2,3x4-2,3x5-2的平均数大于0
C tpiee :uId: tpiee .数据x2,x3,x4,x5的方差大于s2
D.数据x2,x3,x4,x5的平均数大于
10.如图,函数f(x)=A sin(ωx+φ)(A>0,ω>0,φ≤)的图象与x轴的其中两个交点为A,B,与y轴交于点C,D为线段BC的中点,OB=OC,OA=2,AD=,则
A.f(x)的最小正周期为12π
B.f(x)的图象关于直线x=8对称
C.f(x)在[5,7]单调递减
D.f(-x+2)为奇函数
11.在棱长为1的正方体ABCD-A1B1C1D1中,以A,C1为焦点的椭圆,绕着轴AC1旋转180°得到的旋转体称为椭球AC1,椭圆的长轴就是椭球的长轴,若椭球AC1的长轴长为2,则下列结论中正确的是
A.椭球AC1的表面与正方体ABCD-A1B1C1D1的六个面都有交线
B.在正方体ABCD-A1B1C1D1的所有棱中,只有六条棱与椭球AC1的表面相交
C.若椭球AC1的表面与正方体ABCD-A1B1C1D1的某条棱相交,则交点必是该棱的一个三等分点
D.椭球AC1的表面与正方体ABCD-A1B1C1D1的一个面的交线是椭圆的一段
三、填空题:本题共 qpyippe :fId: qpyippe 3小题,每小题5分,共15分.
12.的展开式中x-7的系数是 .
13.已知数列{an}满足(-1)n+1 an+2+(-1)n an=3(-1)n+1(n∈N*),若a1=a2=1,则{an}的前20项和S20= .
14.已知抛物线C:y2=4x的焦点为F,过F的直线l与C交于A,B两点.过A作C的切线m及平行于x轴的直线m',过F作平行于m的直线交m'于M,过B作C的切线n及平行于x轴的直线n',过F作平行于n的直线交n'于N.若|AM|-|BN|=,则点A的横坐标为 .
四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15.(13分)
如图,在平面四边形ABCD中,AB=AD=4,BC=6.
(I)若A=,C=,求sin∠BDC的值;
(II)若CD=2,cs A=3cs C,求四边形ABCD的面积.
16.(15分)
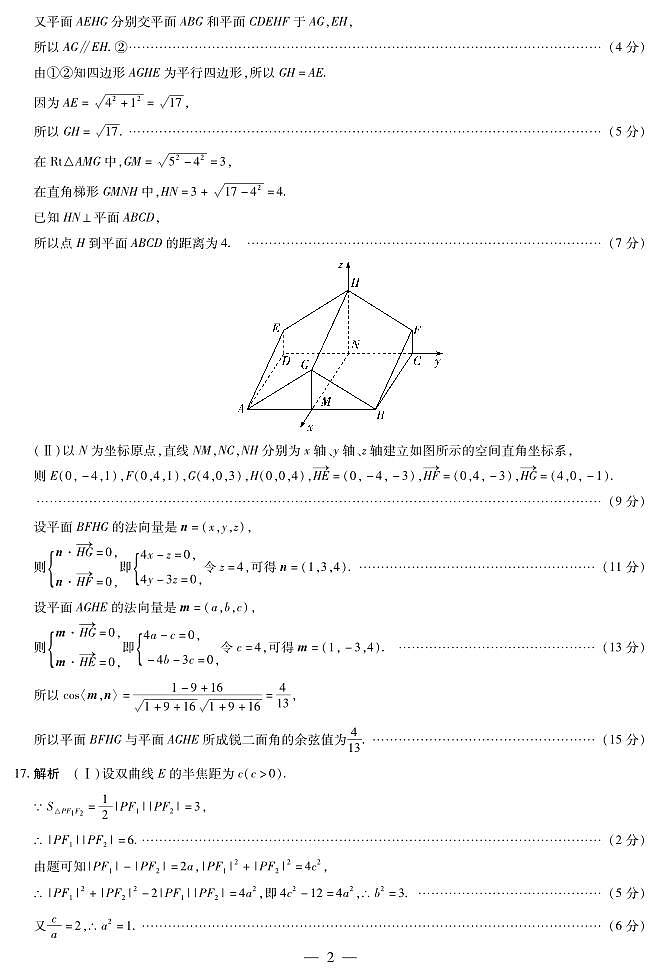
2023年12月19日至20日,中央农村工作会议在北京召开,习近平主席对“三农”工作作出指示.某地区为响应习近平主席的号召,积极发展特色农业,建设蔬菜大棚.如图所示的七面体ABG-CDEHF是一个放置在地面上的蔬菜大棚钢架,四边形ABCD是矩形,AB=8m,AD=4m,ED=CF=1m,且ED,CF都垂直于平面ABCD,GA=GB=5m,HE=HF,平面ABG⊥平面ABCD.
(I)求点H到平面ABCD的距离;
( TPIEE :uId: TPIEE II)求平面BFHG与平面AGHE所成锐二面角的余弦值.
17.(15分)
已知双曲线E:=1(a>0,b>0)的左、右焦点分别为F1,F2,离心率为2,P是E的右支上一点,且PF1⊥PF2,∆PF1F2的面积为3.
(I)求E的方程;
(II)若E的左、右顶点分别为A,B,过点F2的直线l与E的右支交于M,N两点,直线AM和BN的斜率分别记为kAM和kBN,求的最小值
18.(17分)
某校在90周年校庆到来之际,为了丰富教师的学习和生活,特举行了答题竞赛.在竞赛中,每位参赛教师答题若干次,每一次答题的赋分方法如下:第1次答题,答对得20分,答错得10分,从第2次答题开始,答对则获得上一次答题所得分数两倍的得分,答错得10分.教师甲参加答题竞赛,每次答对的概率均为,每次答题是否答对互不影响.
(I)求甲前3次答题的得分之和为70分的概率.
(II)记甲第i次答题所得分数Xi(i∈N*)的数学期望为E(Xi).
(i)求E(X1),E(X2),E(X3),并猜想当i≥2时,E(Xi)与E(Xi-1)之间的关系式;
(ii)若>320,求n的最小值.
19.(17分)
已知函数 QPYIPPE :fId: QPYIPPE f(x)=(2x-a)e2x-bex的图象在点(0,f(0))处的切线方程为y=-x-.
(I)求f(x)的解析式;
(II)证明:x∈(0,+∞),f(x)>2ln x-2.
参考数据:2024-03-28T22:21:02.394395≈2.23.
2024年安徽省示范高中皖北协作区第26届高三联考数学试题及答案: 这是一份2024年安徽省示范高中皖北协作区第26届高三联考数学试题及答案,文件包含数学试卷pdf、数学答案pdf等2份试卷配套教学资源,其中试卷共12页, 欢迎下载使用。
2024年安徽省示范高中皖北协作区第26届高三联考 数学试题: 这是一份2024年安徽省示范高中皖北协作区第26届高三联考 数学试题,文件包含数学试卷pdf、数学答案pdf等2份试卷配套教学资源,其中试卷共12页, 欢迎下载使用。
2023届安徽省示范高中皖北协作区高三下学期联考数学试题: 这是一份2023届安徽省示范高中皖北协作区高三下学期联考数学试题,文件包含数学300C答案pdf、2023年安徽省示范高中皖北协作区第25届高三联考数学pdfpdf等2份试卷配套教学资源,其中试卷共10页, 欢迎下载使用。










