福建省百校联考2024届高三下学期正月开学考试数学试卷(含答案)

这是一份福建省百校联考2024届高三下学期正月开学考试数学试卷(含答案)，共18页。试卷主要包含了选择题，多项选择题，填空题，解答题等内容，欢迎下载使用。


一、选择题
1．已知集合,则( )
A.B.C.D.
2．复数 在复平面内所对应的点所在的象限为( )
A.第一象限B.第二象限C.第三象限D.第四象限
3．过点的直线l与圆相切,则直线l的方程为( )
A.B.C.D.
4．已知,则( )
A.-4B.C.D.
5．如图是两个底面半径都为1的圆锥底面重合在一起构成的几何体,上面圆锥的侧面积是下面圆锥侧面积的2倍,,则( )
A.B.C.D.3
6．如图,在边长为2的菱形中,,点E,F分别在边CB,CD上,且若 ,则( )
A.B.C.1D.
7．已知函数在区问上存任最小值, 则实数a的取值范围为( )
A.B.C.D.
8．已知椭圆的左、右焦点分别,椭圆的长轴长为,短轴长为2,P为直线上的任意一点, 则的最大值为( )
A.B.C.D.
二、多项选择题
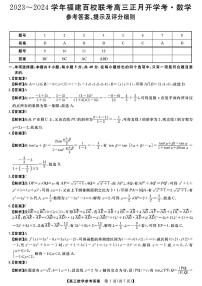
9．据国家统计局网站 2023年9月15日消息, 8 月份, 社会消费品零售总额为 37933 亿元, 同比增长(同比-一般情况下是指本年第N月与去年的第N月比).其中,除汽车以外的消费品答额为 33820 亿元, 增长,月份, 社会消费品零售总额为302281亿元, 同比增长.其中,除汽车以外的消费品零售额为 271888 亿元,增长,年8月至2023年8月社会消费品零售总额同比增速如下:
则下列说法正确的是( )
A.2023年18月份, 社会消费品零售总额的月平均值约为25422.6亿元
B.2022年8月份, 社会消费品零售总额约为36264.8亿元
C.除掉2022年8月至2023年8月社会消费品零售总额同比增速数据的最大值和最小值所得数据的标准差比原数据的标准差小
D.2022年8月至2023年8月社会消费品零售总额同比增速数据的极差比中位数的8倍还多
10．在前n项和为的正项等比数列中,,,则( )
A.B.
C.D.数列中的最大项为
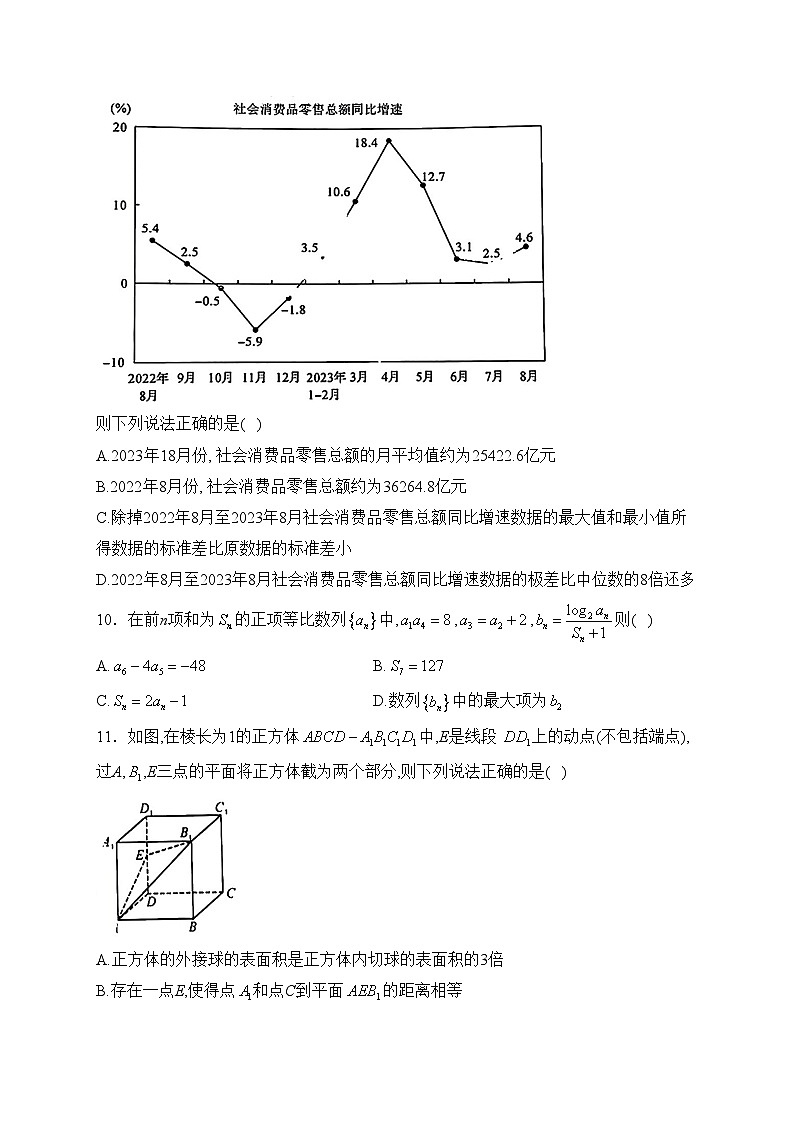
11．如图,在棱长为1的正方体中,E是线段 上的动点(不包括端点), 过A,,E三点的平面将正方体截为两个部分,则下列说法正确的是( )
A.正方体的外接球的表面积是正方体内切球的表面积的3倍
B.存在一点E,使得点和点C到平面的距离相等
C.正方体被平面所截得的截面的面积随着的增大而增大
D.当正方体被平面所截得的上部分的几何体的体积为时,E是的中点
12．在平面直角坐标系中, 已知双曲线的右顶点为A, 直线 l与以O为圆心,为半径的国相切, 切点为P.则( )
A.双曲线C的离心率为
B.当直线与双曲线C的一条浙近线近合时, 直线l过双曲线C的一个焦点
C.当直线l与双曲线C的一条浙近线平行时,若直线l与双曲线C的交点为Q,则
D.若直线l与双曲线C的两条浙近线分別交于D, E两点与双州线C分别交于M,N两点，则
三、填空题
13．设A,B是一个随机试验中的两个水件, 若,,,则______________.
14．已知 的展开式中的系数为 240 ,则实数______________.
15．已知函数的值域为R, 则实数a的取值范围为___________.
16．方程 的最小的29个非负实数解之和为____________.
四、解答题
17．已知正项数列中,,.
(1)求数列的通项公式;
(2)记数列 的前n项和,求满足的正整数n的集合.
18．在中, 内角A, B, C所对的边分別为a, b, c,且 .
(1)求A;
(2)过点A作的垂线与的延长线交于点D,,的面积为,求的周长.
19．如图, 在四棱锥中,底面是直角梯形, ,，，.
(1)证明:平面;
(2)已知,，平面底面,若平面与平面的夹角的余弦值为,求.
20．驾驶员考 (机动车驾驶员考试) 是由公安局车管所举办的资格考试, 只有通过驾驶员考试才能取得驾照, 才能合法的驾驶机动车辆. 考试内容和合格标准全国统一, 根据不同准驾车型规定相应的考试项目. 机动车驾驶人考试内容分为道路交通安全法律、法规和相关知识考式科目(以下简称“科目一”)、场地驾驶技能考试科目(以下简称“科目二”)、道路驾驶技能和安全文明驾驶常识考试科目 (以下简称“科目三”). 申请人科目一、科目二、科目三考试均合格后, 就可以领取驾驶证. 某驾校经统计, 驾驶员科目一考试平均通过的概率为 , 科目二平均通过的概率为,科目三平均通过的概率为,该驾校王教练手下有4名学员参加驾驶员考试.
(1)记这4名学员参加驾驶员考试, 通过考试并领取驾驶证的人数为X, 求X的分布列和数学期望及方差;
(2)根涺调查发现, 学员在学完固定的学时后, 每增加一天学习, 没有通过考试畣到驾驶证的概率会降为原来的0.4,请问这 4 名学员至少要增加多少天的学习, 才能保证这 4 名学员都能通过考试并领取驾驶证? (我们把概率超过0.99的事件称为必然事件,认为在一次试验中必然事件一定会发生)
参考数据：，
21．已知拋物线的焦点为F,过扰物线C的准线上任意一点P作不过焦点F的直线l与苭物线C相交于M,N两点, 当直线l的方程为时,.
(1)求拖物线C的标准方程;
(2)证明: 直线是的外角平分线.
22．已知函数，其中.
(1)讨论函数的单调性;
(2)若, 证明:函数有唯一的零点;
(3)若,求实数a的取值范围.
参考答案
1．答案：D
解析：由,可得 ,故选：D.
2．答案：A
解析：由，可得复数z在复平面内所对应的点所在的像限为第一象限,故选：A.
3．答案：B
解析：由点P在圆C上, 又由直线的斜率为,可得直线l的斜率为2 ,则直线l的方程为.故选：B.
4．答案：B
解析：由 ,
有，
故选：B.
5．答案：C
解析：高,有 ,
由,有,可得，
可得 , 又由上下圆锥侧面积之比为, 可得 ,有，
有.代入 整理为,
解得,可得 .
故选：C.
6．答案：C
解析：设 ,可得 ,有，
，有
，
又由 , 有, 解得，(舍),可得.
故选：C.
7．答案：A
解析：由 ,
可得函数的单调增区间为,减区间，，
当时,,
解得 或,有 解得.
故选：A.
8．答案：D
解析：由题意有,，设直线与x轴的交点为Q,设,
有，，
可得，
当且仅当 时取等号, 可得的最大值为,
故选：D.
9．答案：BC
解析：对于A选项, 由 2023 年 月份, 社会消费品零售总额为 302281 亿元, 可得社会消费品零售总额的月平均值约为 亿元,故A 选项错误;
对于B选项, 由 2023 年 8 月份,社会消费品零售总额为 37933 亿元, 同比增长, 可得2022年8月份, 社会消费品零售总额约为 亿元, 故B选项正确;
对于C 选项, 由图表可知去掉-5.9,18.4数据更集中,标准差相对于原数据来说变小了,故C选项正确;
对于D选项, 极差为, 中位数为,可得 ,故D选项错误.
故选：BC.
10．答案：BC
解析：设等比数列 的公比为q,
由, 有,联立方程
解得 或(舍去),有,
可得.
对于A选项, 由,有,故A选项错误;
对于B选项,,故B选项正确;
对于C选项,由,有,故C选项正确;
对于D选项,由,
令, 有 ,
可得有，
可得数列中的最大项为或,故D选项错误,
故选：BC.
11．答案：AC
解析：对于A选项, 正方体外接球的半径为,内切球的半径为.可得正方体的外接球的表面积是正方体内切球的表面积的 倍. 故A选项正确;
对于B选项,由点和点B到平面的距离相等,若点和点C到平面的距离相等, 必有 平面,又由,可得平面,与平面矛盾,故B选项错误;
对于C选项, 如图, 在上取一点F,使得, 连接,
设,由,可得平面为过A,,E三点的截面,
在梯形中,,,,
,
梯形的高为,
梯形的面积为,
令,
有,可得函数单调递增. 可得正方体被平面所截得的截面面积随着的增大而增大. 故C选项正确;
对于D选项，,
,
被平面所截得的上部分的几何体的体积为,整理为, 解得 ,故D选项错误.
故选：AC.
12．答案：ABD
解析：
13．答案：
解析：有, 有,
又由，有. 可 .
14．答案：
解析：的展开式中无含项, 含的项为，中含的项为, 则 .解得 .
15．答案：
解析：①当时, 若,可得, 若,函数的值域不可能为R;
②当时,函数在，上单调递增,
若函数 的值域为R, 只需 , 可得.
由上知, 实数a的取值范围为.
16．答案：
解析：方程 可化为 , 因式分解为 .
,解得 或,方程的最小的29个非负实数解中有 10 个是以 0 为首项,为公差的等差数列. 其和为;
有10 个是以为首项,为公差的等差数列,其和为；
有9个是以为首项, 为公差的等差数列, 其和为.
可得方程的最小的 29 个非负实数解之和为.
17．答案： (1)
(2)
解析：(1)由,有,
有, 有,
可得数列是公差为 1 的等差数列,
有,
可得数列的通项公式为;
(2)由,
有.
不等式可化为,解得,可得满足的正整数n的集合为.
18．答案： (1)
(2)
解析：(1) 由正弦定理有,
两边除以.有,
由二倍角公式,有,
整理为,
上式因式分解为,
解得或 (舍去),
又由, 可得;
(2)由,有,
又由,可得,
有，
可得，
又由的面积为及,有 ,
代入,可得,，
又由,有, 代入,可得,
在中,由余弦定理,有,
有的周长为.
19．答案：(1)见解析
(2)
解析：(1) 证明: 如图, 连接与相交于点O,连接,
，，
，，
，平面平面，平面;
(2)在 中,，
可得
由,平面 底面, 过点A作底面的垂线l,
垂线在平面内,以A为坐标原点, , , 直线l分别为x, y, z轴建立如图所示的空间直角坐标系,有,,
又由,可得点P的坐标为,
又由，
有,
设,可得点B的坐标为, 点C的坐标为 ,
设平面的法向量为,由,,
有 取,可得平面的一个法向量为.设平面的法向量为,由,
有取,,可得平面的一个法向量为.
由,,有,
又由平面与平面的夹角的余弦值为,有,
化简为.解得或(舍).
由上知.
20．答案： (1)分布列见解析,，
(2)这4名学员至少要增加6天的学习,才能保证这4名学员都能通过考试并领取驾驶证
解析：(1)1名学员通过考试并领取驾驶证的概率为,
根据题意可知.
X的取值分别为0,1,2,3,4,
，
，
，
，
.
故X的分布列为:
，；
(2)增加k(k为正整数)天学习后, 每位学员通过考试拿到驾驶证的概率为，
若这4名学员都能通过考试并领取驾驶证,有,
有,有,有,
又由,
可得,
故这4名学员至少要增加6天的学习,才能保证这4名学员都能通过考试并领取驾驶证.
21．答案： (1)
(2)见解析
解析：(1)设M, N的坐标分别为,
由抛物线的定义有,可得,,
联立方程 消去y后獘理为,有,
有 ,整理为,解得或(舍去),
故抛物线C的标准方程为;
(2)证明: 直线l的斜率为,
直线l的方程为 代入后整理为,
令,得, 可得点P的坐标为,
焦点F的坐标为,直线的方程为,
整理为,
点P到直线的距离为
同理点P到直线的距离为,
由及直线l与拋物线C的位置关系, 可得直线是的外角平分线.
22．答案：(1)详解见解析
(2)见解析
(3)
解析：(1)函数的定义域为,
，
①当时,解不等式,有,函数的减区间为,增区间为;
②当时,,若,，可得;若 ,，
可得;若,可得.故有, 函数单调递增,增区间为 ,没有减区间;
③当时, 解不等式 ,有或,故函数的增区间为 ,，减区间为 ；
④当时,解不等式.有或,故函数的增区间为 ,减区间为；
(2) 证明: 若,函数的减区间为,增区间为,
当时,由,有,
由上知, 函数有唯一的零点;
(3) 由(2) 知, 若 , 必有,又由 ,可得,
又由,不等式可化为,
设，
有,
当且时,, 可得 ,
当且时,,可得,
当时,函数 单调递增, 故存在正数m使得 ,
若,有,有,与 矛盾,可得,
当时,;当时,,可得函数的减区间为,
增区间为,
若, 必有 ,
有,又由 ,
有,有 ,
有.
又由 , 有 . 可得,
有,可得 ,
由,及, 可得 ,
若,则实数a的取值范围为 .
X
0
1
2
3
4
P