

中考数学一轮复习专题3.4 圆周角、圆内接四边形【十大题型】(举一反三)(北师大版)(原卷版)
展开TOC \ "1-3" \h \u
\l "_Tc11969" 【题型1 圆周角的运用】 PAGEREF _Tc11969 \h 2
\l "_Tc8578" 【题型2 圆内接四边形的运用】 PAGEREF _Tc8578 \h 3
\l "_Tc9909" 【题型3 利用圆的有关性质求值】 PAGEREF _Tc9909 \h 4
\l "_Tc4839" 【题型4 利用圆的有关性质进行证明】 PAGEREF _Tc4839 \h 5
\l "_Tc24163" 【题型5 翻折中的圆的有关性质的运用】 PAGEREF _Tc24163 \h 7
\l "_Tc360" 【题型6 利用圆的有关性质求最值】 PAGEREF _Tc360 \h 9
\l "_Tc9945" 【题型7 利用圆的有关性质求取值范围】 PAGEREF _Tc9945 \h 10
\l "_Tc28216" 【题型8 利用圆的有关性质探究角或线段间的关系】 PAGEREF _Tc28216 \h 11
\l "_Tc1906" 【题型9 利用圆的有关性质判断多结论问题】 PAGEREF _Tc1906 \h 13
\l "_Tc27247" 【题型10 构造圆利用圆周角解决三角形或四边形中的问题】 PAGEREF _Tc27247 \h 14
【知识点1 圆周角定理及其推论】
【题型1 圆周角的运用】
【例1】(2023春·山东泰安·九年级东平县实验中学校考期末)如图,⊙O的直径是AB,∠BPQ=45°,圆的半径是4,则弦BQ的长是( ).
A.43B.42C.23D.22
【变式1-1】(2023春·广西玉林·九年级统考期末)如图,在△ABC中,AB为⊙O的直径,已知AB=4,CD=1,∠B=55°,∠C=65°,则BC= .
【变式1-2】(2023春·江西九江·九年级校考期中)如图,△ABC内接于☉O,AC=BC,连接OB,若∠C=52°,则∠OBC的度数为 .
【变式1-3】(2023春·湖北省直辖县级单位·九年级统考期末)如图,AB为半圆的直径,AB=10,点O到弦AC的距离为4,点P从出发沿BA方向向点A以每秒1个单位长度的速度运动,连接CP,当△APC为等腰三角形时,点P运动的时间是( )
A.145或4B.145或5C.4或5D.145,4或5
【知识点2 圆内接四边形】
【题型2 圆内接四边形的运用】
【例2】(2023春·浙江衢州·九年级校联考期中)如图,在△ABC中,AB=AC.⊙O是△ABC的外接圆,D为弧AC的中点,E为BA延长线上一点.
(1)求证:∠B=2∠ACD;
(2)若∠ACD=35°,求∠DAE的度数.
【变式2-1】(2023春·陕西西安·九年级高新一中校考期中)如图,四边形ABCD是⊙O的内接四边形,BE是⊙O的直径,连接AE,若∠BCD=2∠BAD,若连接OD,则∠DOE的度数是( )
A.30°B.35°C.45°D.60°
【变式2-2】(2023春·浙江·九年级期中)如图,⊙O的内接四边形ABCD两组对边的延长线分别交于点E、F,若∠E=α,∠F=β,且α≠β,则∠A= (用含有a、β的代数式表示).
【变式2-3】(2023春·辽宁大连·九年级统考期末)如图,以△ABC的边AB为直径作⊙O交AC于D且OD∥BC,⊙O交BC于点E.
(1)求证:CD=DE;
(2)若AB=12,AD=4,求CE的长度.
【题型3 利用圆的有关性质求值】
【例3】(2023春·四川德阳·九年级四川省德阳中学校校考期中)如图,在△ABC中,∠ACB=90°,过B,C两点的⊙O交AC于点D,交AB于点E,连接EO并延长交⊙O于点F.连接BF,CF,若∠EDC=135°,AE=2,BE=4,则CF的值为( ).
A.10B.22C.23D.3
【变式3-1】(2023春·湖南长沙·九年级统考期末)如图,⊙O中,OA⊥BC,∠B=50°,则∠D的度数为( )
A.20°B.50°C.40°D.25°
【变式3-2】(2023春·山东滨州·九年级统考期中)如图,⊙O为△ABC的外接圆,AD⊥BC,垂足为点D,直径AE平分∠BAD,交BC于点F,连接BE.
(1)求证:BE=BF;
(2)若AB=10,BF=5,求EF:AF的值.
【变式3-3】(2023春·广东汕头·九年级汕头市龙湖实验中学校考期中)如图1,四边形ADBC内接于⊙O,E为BD延长线上一点,AD平分∠EDC.
(1)求证:AB=AC;
(2)若△ABC为等边三角形,则∠EDA= 度;(直接写答案)
(3)如图2,若CD为直径,过A点作AE⊥BD于E,且DB=AE=2,求⊙O的半径.
【题型4 利用圆的有关性质进行证明】
【例4】(2023春·广东广州·九年级广东广雅中学校考期末)如图,CD是△ABC的外角∠ECB的角平分线,与△ABC的外接圆⊙O交于点D,∠ECB=120°.
(1)求AB所对圆心角的度数;
(2)连DB,DA,求证:DA=DB;
(3)探究线段CD,CA,CB之间的数量关系,并证明你的结论.
【变式4-1】(2023春·浙江金华·九年级校考期中)如图,已知圆O的直径AB垂直于弦CD于点E,连接CO并延长交AD于点F,且CF⊥AD.证明:E是OB的中点.
【变式4-2】(2023春·山西长治·九年级统考期末)阅读材料,解答问题:
关于圆的引理
古希腊数学家、物理学家阿基米德流传于世的数学著作有10余种,下面是《阿基米德全集》的《引理集》中记载的一个命题:
如图1,AB是⊙O的弦,点C在⊙O上,CD⊥AB于点D,在弦AB上取点E,使DE=AD,点F是BC上的一点,且CF=CA,连接BF,则BF=BE.
小颖对这个问题很感兴趣,经过思考,写出了下面的证明过程:
证明:如图2,连接CA,CE,CF,BC,
∵CD⊥AB于点D,DE=AD,
∴CA=CE.
∴∠CAE=∠CEA.
∵ CF=CA,
∴CF=CA(依据1),∠CBF=∠CBA.
∵四边形ABFC内接于⊙O,
∴∠CAB+∠CFB=180°.(依据2)
……
(1)上述证明过程中的依据1为 ,依据2为 ;
(2)将上述证明过程补充完整.
【变式4-3】(2023春·江苏泰州·九年级校考期末)已知⊙O为△ACD的外接圆,AD=CD.
(1)如图1,延长AD至点B,使BD=AD,连接CB.
①求证:△ABC为直角三角形;
②若⊙O的半径为4,AD=5,求BC的值;
(2)如图2,若∠ADC=90°,E为⊙O上的一点,且点D,E位于AC两侧,作△ADE关于AD对称的图形△ADQ,连接QC,试猜想QA,QC,QD三者之间的数量关系并给予证明.
【题型5 翻折中的圆的有关性质的运用】
【例5】(2023春·江苏无锡·九年级统考期中)如图,将⊙O上的BC沿弦BC翻折交半径OA于点D,再将BD沿BD翻折交BC于点E,连接DE. 若AD=2OD,则DEAB的值为( )
A.36B.63C.33D.66
【变式5-1】(2023春·湖北恩施·九年级期末)如图,AB为⊙O的一条弦,C为⊙O上一点,OC∥AB.将劣弧AB沿弦AB翻折,交翻折后的弧AB交AC于点D.若D为翻折后弧AB的中点,则∠ABC=( )
A.110°B.112.5°C.115°D.117.5°
【变式5-2】(2023春·浙江宁波·九年级校考期中)如图,在⊙O中,AB为直径,C为圆上一点,将劣弧AC沿弦AC翻折,交AB于点D,连接CD,若点D与圆心O不重合,∠BAC=25°,则∠DCA= .
【变式5-3】(2023春·浙江金华·九年级浙江省义乌市稠江中学校考期中)在⊙O中,AB为直径,点C为圆上一点,将劣弧沿弦AC翻折交AB于点D,连接CD.
(1)如图1,若点D与圆心O重合,AC=3,求⊙O的半径r;
(2)如图2,若点D与圆心O不重合,∠BAC=20∘,请求出∠DCA的度数.
(3)如图2,如果AD=6,DB=2,求AC的长.
【题型6 利用圆的有关性质求最值】
【例6】(2023春·浙江衢州·九年级校联考期中)如图,△ABC中,AB=23,∠ACB=75°,∠ABC=60°,D是线段BC上的一个动点,以AD为直径画⊙O,分别交AB,AC于E,F,连接EF,则∠BAC= ;EF的最小值为 .
【变式6-1】(2023春·北京密云·九年级统考期末)如图,⊙O的弦AB长为2,CD是⊙O的直径,∠ADB=30°,∠ADC=15°.
①⊙O的半径长为 .
②P是CD上的动点,则PA+PB的最小值是 .
【变式6-2】(2023春·湖南湘西·九年级统考期末)如图,在正方形ABCD中,AB=4,以边CD为直径作半圆O,E是半圆O上的动点,EF⊥DA于点F,EP⊥AB于点P,设EF=x,EP=y,则x2+y2的最小值是( )
A.23−1B.4−23C.25−1D.25−2
【变式6-3】(2023春·辽宁沈阳·九年级沈阳市第七中学校考期末)如图,已知以BC为直径的⊙O,A为弧BC中点,P为弧AC上任意一点,AD⊥AP交BP于D,连CD.若BC=6,则CD的最小值为 .
【题型7 利用圆的有关性质求取值范围】
【例7】(2023春·湖北武汉·九年级校考期末)如图,△ABC的两个顶点A、B在⊙O上,⊙O的半径为2,∠BAC=90°,AB=AC,若动点B在⊙O上运动,OC=m,则m的取值范围是 .
【变式7-1】(2023春·新疆乌鲁木齐·九年级校考期中)如图,弧BE是半径为6的圆D的14圆周,C点是BE上的任意一点,△ABD是等边三角形,则四边形ABCD的周长P的取值范围是( )
A.12<P≤18B.18<P≤24C.18<P≤18+62D.12<P≤12+62
【变式7-2】(2023春·福建福州·九年级校考期中)如图,⊙O的直径为10,A、B、C、D是⊙O上的四个动点,且AB=6,CD=8,若点E、F分别是弦AB、CD的中点,则线段EF长度的取值范围是()
A.1≤EF≤7B.2≤EF≤5C.1<EF<7D.1≤EF≤6
【变式7-3】(2023春·江苏南京·九年级统考期中)如图,在平面直角坐标系xOy中,⊙O的半径是1.过⊙O上一点P作等边三角形PDE,使点D,E分别落在x轴、y轴上,则PD的取值范围是 .
【题型8 利用圆的有关性质探究角或线段间的关系】
【例8】(2023·河北石家庄·统考一模)如图,AB是半圆O的直径,C、D、E三点依次在半圆O上,若∠C=α,∠E=β,则α与β之间的关系是( )
A.α+β=270°B.α+β=180°C.β=α+90°D.β=12α+90°
【变式8-1】(2023·湖北襄阳·九年级校考阶段练习)如图,等边△ABC内接于⊙O,P是AB上任意一点(不与点A、B重合),连AP、BP,过点C作CM//BP交PA的延长线于点M.
(1)求∠APC和∠BPC的度数
(2)探究PA、PB、PM之间的关系
(3)若PA=1,PB=2,求四边形PBCM的面积.
【变式8-2】(2023春·安徽·九年级专题练习)如图,四边形ABCD内接于⊙O,AC是⊙O的直径,AB=BC,延长DA到点E,使得BE=BD.
(1)若AF平分∠CAD,求证:BA=BF;
(2)试探究线段AD,CD与BD之间的数量关系.
【变式8-3】(2023·江苏·九年级假期作业)小明学习了垂径定理,做了下面的探究,请根据题目要求帮小明完成探究.
(1)更换定理的题设和结论可以得到许多真命题.如图1,在⊙O中,C是劣弧AB的中点,直线CD⊥AB于点E,则AE=BE.请证明此结论;
(2)从圆上任意一点出发的两条弦所组成的折线,成为该圆的一条折弦.如图2,PA,PB组成⊙O的一条折弦.C是劣弧AB的中点,直线CD⊥PA于点E,则AE=PE+PB.可以通过延长DB、AP相交于点F,再连接AD证明结论成立.请写出证明过程;
(3)如图3,PA,PB组成⊙O的一条折弦.C是优弧ACB的中点,直线CD⊥PA于点E,则AE,PE与PB之间存在怎样的数量关系?写出结论,不必证明.
【题型9 利用圆的有关性质判断多结论问题】
【例9】(2023春·江苏镇江·九年级统考期中)如图,点A、B、C是⊙O上的点,且∠ACB=90°,AC=6,BC=8,∠ACB的平分线交⊙O于D,下列4个判断:①⊙O的半径为5;②CD的长为72;③在BC弦所在直线上存在3个不同的点E,使得△CDE是等腰三角形;④在BC弦所在直线上存在2个不同的点F,使得△CDF是直角三角形;正确判断的个数有( )
A.1B.2C.3D.4
【变式9-1】(2023春·广东湛江·九年级统考期末)如图所示,MN是⊙O的直径,作AB⊥MN,垂足为点D,连接AM,AN,点C为AN上一点,且AC=AM,连接CM,交AB于点E,交AN于点F,现给出以下结论:①AD=BD;②∠MAN=90°;③AM=BM;④∠ACM+∠ANM=∠MOB;⑤AE=12MF.
其中正确结论的个数是( )
A.2B.3C.4D.5
【变式9-2】(2023春·全国·九年级统考期末)已知如图,点O为△ABD的外心,点C为直径BD下方弧BCD上一点,且不与点B,D重合,∠ACB=∠ABD=45°,则下列对AC,BC,CD之间的数量关系判断正确的是( )
A.AC=BC+CD B.2 AC=BC+CD C.3 AC=BC+CD D.2AC=BC+CD
【变式9-3】(2023春·浙江·九年级期末)在一次探究活动中,方方完成了如下的尺规画图过程:第一步:在半径为1的⊙O上任取一点A,连续以1为半径在⊙O上截取AB=BC=CD;第二步:分别以A、D为圆心A到C的距离为半径画弧,两弧交于E,以A为圆心O到E的距离为半径画弧,交⊙O于F.画图后,他得出两个结论:①AF的长为2;②△ACF的面积为3+34,则( )
A.①正确,②正确 B.①正确,②错误 C.①错误,②正确 D.①错误,②错误
【题型10 构造圆利用圆周角解决三角形或四边形中的问题】
【例10】(2023春·安徽六安·九年级校考期末)如图,在Rt△ABC中,AB⊥BC,AB=6,BC=4,P是△ABC内部的一个动点,连接PC,且满足∠PAB=∠PBC,过点P作PD⊥BC于点D,则∠APB= ;当线段CP最短时,△BCP的面积为
【变式10-1】(2023春·福建厦门·九年级厦门市第五中学校考期中)在△ABC中,∠ACB=90°,AC=BC=2,把△ABC绕点B顺时针旋转得到△DBE(点A与D对应).
(1)如图,若点E落在边AB上,连接AD,求AE的长;
(2)如图,若旋转角度为60°,连接AE.求AE的长;
(3)如图,若旋转角度为α45°≤α≤90°,连接AD,BF⊥AD,垂足为F.求证:C,E,F三点在同一直线上.
【变式10-2】(2023春·重庆开州·九年级统考期末)如图,以直角三角形ABC的斜边AB为边在三角形ABC的同侧作正方形ABDE,正方形的对角线AD,BE相交于点O,连接CO,如果AC=1,CO=22,则正方形ABDE的面积为( )
A.20B.22C.24D.26
【变式10-3】(2023春·吉林长春·九年级校考期末)如图,菱形ABCD的边长为8,∠A=60°,E是AD中点,动点P从点A出发,沿折线AB−BD以每秒1个单位长度的速度向终点D运动,连结PE,作A关于直线PE的对称点A′,连结A′E、A′P.设P的运动时间为t秒.
(1)点D到AB的距离是 .
(2)直接写出A′B的最小值.
(3)当A′落在菱形ABCD的边上时,求△A′PE的面积.
(4)当A′P垂直于菱形ABCD的一边时,直接写出t的值.圆周角定理
定理:圆周角的度数等于它所对的弧的圆心角度数的一半
是所对的圆心角,
是所对的圆周角,
推论1:同弧或等弧所对的圆周角相等
和都是所对的圆周角
推论2:直径所对的圆周角是直角,的圆周角所对的弦是直径
是的直径
是所对的圆周角
是所对的圆周角
是的直径
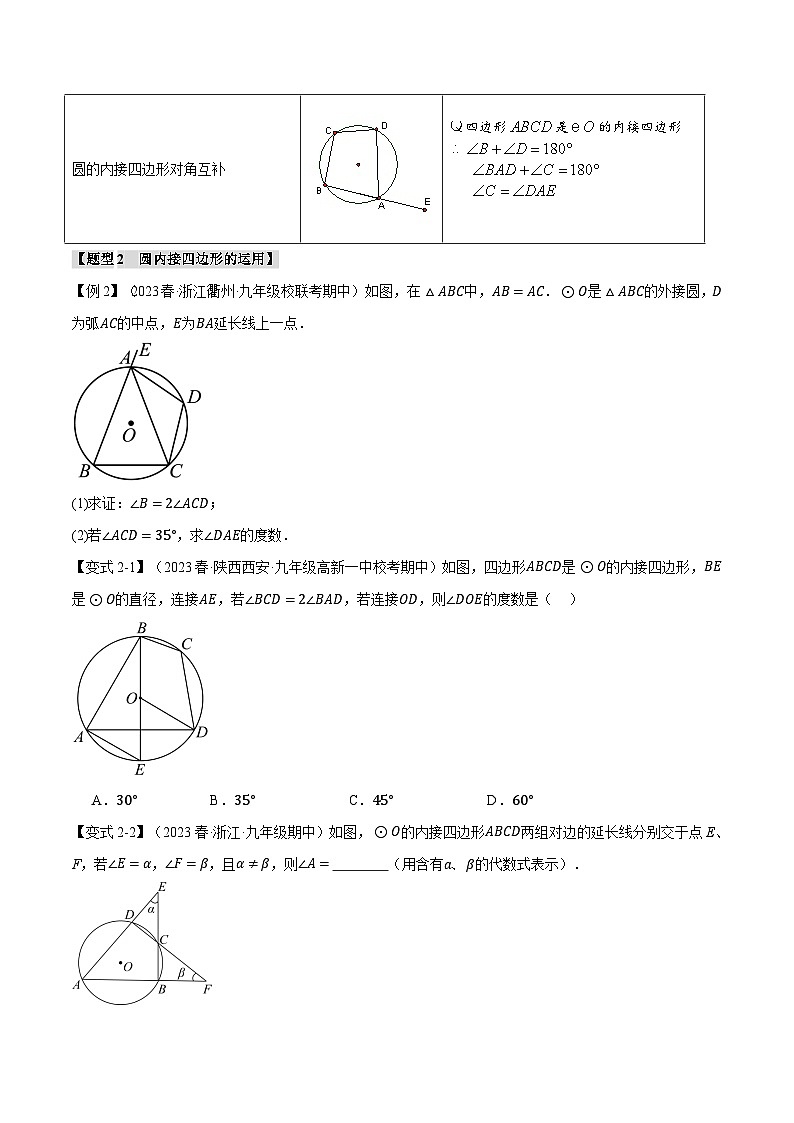
圆的内接四边形对角互补
四边形是的内接四边形
中考数学一轮复习 题型举一反三 专题02 整式与因式分解【十大题型】(举一反三)(2份打包,原卷版+解析版): 这是一份中考数学一轮复习 题型举一反三 专题02 整式与因式分解【十大题型】(举一反三)(2份打包,原卷版+解析版),文件包含中考数学一轮复习题型举一反三专题02整式与因式分解十大题型举一反三原卷版doc、中考数学一轮复习题型举一反三专题02整式与因式分解十大题型举一反三解析版doc等2份试卷配套教学资源,其中试卷共38页, 欢迎下载使用。
中考数学一轮复习专题3.4 圆周角、圆内接四边形【十大题型】(举一反三)(北师大版)(解析版): 这是一份中考数学一轮复习专题3.4 圆周角、圆内接四边形【十大题型】(举一反三)(北师大版)(解析版),共64页。
中考数学一轮复习专题3.3 弧、弦、圆心角【十大题型】(举一反三)(北师大版)(原卷版): 这是一份中考数学一轮复习专题3.3 弧、弦、圆心角【十大题型】(举一反三)(北师大版)(原卷版),共12页。












