福建省厦门市思明区槟榔中学2023-2024学年九年级下学期3月月考模拟数学试卷（含答案）

这是一份福建省厦门市思明区槟榔中学2023-2024学年九年级下学期3月月考模拟数学试卷（含答案），共14页。试卷主要包含了＝，则a＝　 　等内容，欢迎下载使用。

1．（4分）在下列调查中，适宜采用全面调查的是（ ）
A．检测一批电灯泡的使用寿命
B．了解九（1）班学生校服的尺码情况
C．了解我省中学生的视力情况
D．调查重庆《生活麻辣烫》栏目的收视率
2．（4分）要使二次根式有意义，x的值可以是（ ）
A．﹣1B．0C．2D．4
3．（4分）关于x的一元二次方程x2＝1的根是（ ）
A．x＝1B．x1＝1，x2＝﹣1
C．x＝﹣1D．x1＝x2＝1
4．（4分）小区新增了一家快递店，第一天揽件200件，第三天揽件242件，设该快递店揽件日平均增长率为x，根据题意，下面所列方程正确的是（ ）
A．200（1+x）2＝242B．200（1﹣x）2＝242
C．200（1+2x）＝242D．200（1﹣2x）＝242
5．（4分）如图，C，D是⊙O上直径AB两侧的两点，设∠ABC＝32°，则∠BDC＝（ ）
A．64°B．62°C．60°D．58°
6．（4分）下列四个点中，有三个点在同一反比例函数的图象上，则不在这个函数图象上的点是（ ）
A．（5，1）B．（﹣1，5）C．（，3）D．（﹣3，﹣）
7．（4分）大自然中有许多小动物都是“小数学家”，如图1，蜜蜂的蜂巢结构非常精巧、实用而且节省材料，多名学者通过观测研究发现：蜂巢巢房的横截面大都是正六边形．如图2，一个巢房的横截面为正六边形ABCDEF，若对角线AD的长约为8mm，则正六边形ABCDEF的边长为（ ）
A．2mmB．2mmC．2mmD．4mm
8．（4分）已知二次函数y＝x2﹣2x+2（其中x是自变量），当0≤x≤a时，y的最大值为2，y的最小值为1．则a的值为（ ）
A．a＝1B．1≤a＜2C．1＜a≤2D．1≤a≤2
二．填空题（共8小题，满分32分，每小题4分）
9．（4分）已知 a 是锐角，sin（15°+α）＝，则a＝ ．
10．（4分）在等腰三角形ABC中，AB＝AC，∠B＝50°，则∠A＝ °．
11．（4分）抛物线y＝4（x﹣2）2+1的顶点坐标是 ．
12．（4分）若x＝3是关于x的方程x2+3x﹣m2＝0的一个根，则m的值是 ．
13．（4分）一只盒子中有红球10个，白球6个，黑球a个，每个球除颜色外都相同，从中任取一个球，取得“红球”的概率与“不是红球”的概率相同，那么a的值是 ．
14．（4分）如图，在Rt△ABC中，∠C＝90°，∠B＝30°，AB＝8，以点C为圆心，CA的长为半径画弧，交AB于点D，则的长为 ．
15．（4分）如图是一张矩形纸片，点E是BC边上一点，将△ECD沿DE折叠，使点C落在矩形内的点C'处，当点C'恰好为矩形对角线中点时，则∠CBD＝ °；当点C'落在对角线BD上，若A，C'，E共线，且AD＝2时，则CE的长为 ．
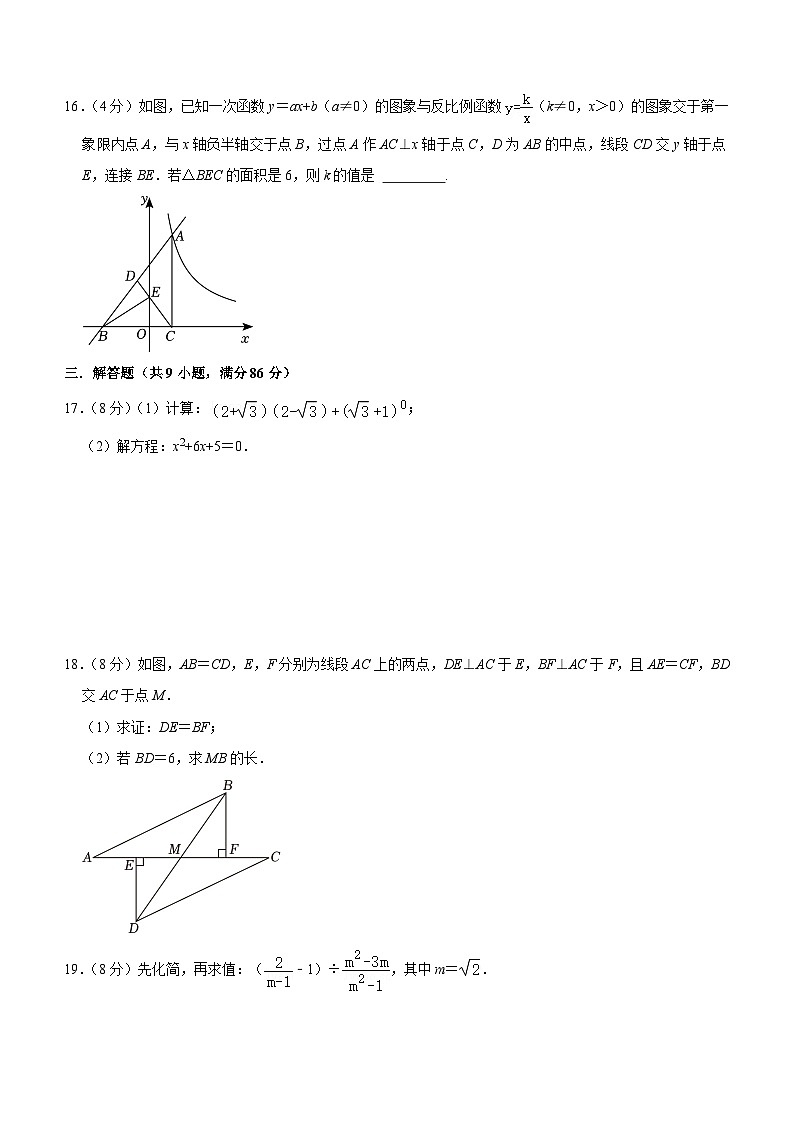
16．（4分）如图，已知一次函数y＝ax+b（a≠0）的图象与反比例函数（k≠0，x＞0）的图象交于第一象限内点A，与x轴负半轴交于点B，过点A作AC⊥x轴于点C，D为AB的中点，线段CD交y轴于点E，连接BE．若△BEC的面积是6，则k的值是 .
三．解答题（共9小题，满分86分）
17．（8分）（1）计算：；
（2）解方程：x2+6x+5＝0．
18．（8分）如图，AB＝CD，E，F分别为线段AC上的两点，DE⊥AC于E，BF⊥AC于F，且AE＝CF，BD交AC于点M．
（1）求证：DE＝BF；
（2）若BD＝6，求MB的长．
（8分）先化简，再求值：（﹣1）÷，其中m＝．
20．（8分）已知BC是⊙O的直径，点D是BC延长线上一点，AB＝AD，AE是⊙O的弦，∠AEC＝30°．
（1）求证：直线AD是⊙O的切线；
（2）若AE⊥BC，垂足为M，⊙O的半径为10，求AE的长．
21．（8分）2023年福建省全民健身运动会，以“我运动，我阳光、我运动，我快乐、我运动，我健康”为主题．活动项目有球类、帆船、游泳、田径、击剑等，某体育兴趣小组收集到了游泳、棒球、帆船、垫球四个项目的比赛规则，并制作了编号分别为A，B，C，D的4张卡片．如图，卡片除了图案和编号外无其他差别，现将它们洗匀后背面朝上放在桌子上．
（1）随机从中抽取一张卡片，抽到“帆船”的概率是 ；
（2）小康同学从中随机抽取一张（不放回），小亮同学从余下的3张卡片中再随机抽取一张，然后根据抽取的卡片讲述对应卡片上的比赛规则，请用列表或画树状图的方法求小康、小亮两人中有一人讲述“游泳”体育项目的比赛规则的概率．
22．（10分）如图，AC是菱形ABCD的对角线．
（1）尺规作图：将△ABC绕点A逆时针旋转得到△ADE，点B旋转后的对应点为D（保留作图痕迹，不写作法）；
（2）在（1）所作的图中，连接BD，CE．
①求证：△ABD～△ACE；
②若tan∠BAC＝，求cs∠DCE的值．
23．（10分）根据以下素材，探索完成任务．
24．（12分）在平面直角坐标系xOy中，抛物线y＝ax2+bx﹣3与x轴交于A（﹣1，0），B（3，0）两点，与y轴交于点C．
（1）求该抛物线的函数解析式；
（2）连接AC，BC，点D是直线BC下方抛物线上的一个的动点（不与B，C重合），
①求△BCD面积的最大值；
②若∠ACO+∠BCD＝∠ABC，求点D的坐标．
25．（14分）已知，四边形ABCD内接于⊙O，，点T在BC的延长线上．
（1）如图1，求证：CD平分∠ACT；
（2）如图2，若AC是⊙O的直径，BE平分∠ABC交CD延长线于E，交⊙O于F，连接AE，AF，DF．
①求∠AED的度数；
②若，△DEF的面积等于，求AC的长．
福建省厦门市思明区槟榔中学2023-2024学年九年级下学期数学3月月考模拟试卷（答案）
一．选择题（共8小题，满分32分，每小题4分）
1．（4分）在下列调查中，适宜采用全面调查的是（ ）
A．检测一批电灯泡的使用寿命
B．了解九（1）班学生校服的尺码情况
C．了解我省中学生的视力情况
D．调查重庆《生活麻辣烫》栏目的收视率
【答案】B
2．（4分）要使二次根式有意义，x的值可以是（ ）
A．﹣1B．0C．2D．4
【答案】D
3．（4分）关于x的一元二次方程x2＝1的根是（ ）
A．x＝1B．x1＝1，x2＝﹣1
C．x＝﹣1D．x1＝x2＝1
【答案】B
4．（4分）小区新增了一家快递店，第一天揽件200件，第三天揽件242件，设该快递店揽件日平均增长率为x，根据题意，下面所列方程正确的是（ ）
A．200（1+x）2＝242B．200（1﹣x）2＝242
C．200（1+2x）＝242D．200（1﹣2x）＝242
【答案】A
5．（4分）如图，C，D是⊙O上直径AB两侧的两点，设∠ABC＝32°，则∠BDC＝（ ）
A．64°B．62°C．60°D．58°
【答案】D
6．（4分）下列四个点中，有三个点在同一反比例函数的图象上，则不在这个函数图象上的点是（ ）
A．（5，1）B．（﹣1，5）C．（，3）D．（﹣3，﹣）
【答案】B
7．（4分）大自然中有许多小动物都是“小数学家”，如图1，蜜蜂的蜂巢结构非常精巧、实用而且节省材料，多名学者通过观测研究发现：蜂巢巢房的横截面大都是正六边形．如图2，一个巢房的横截面为正六边形ABCDEF，若对角线AD的长约为8mm，则正六边形ABCDEF的边长为（ ）
A．2mmB．2mmC．2mmD．4mm
【答案】D
8．（4分）已知二次函数y＝x2﹣2x+2（其中x是自变量），当0≤x≤a时，y的最大值为2，y的最小值为1．则a的值为（ ）
A．a＝1B．1≤a＜2C．1＜a≤2D．1≤a≤2
【答案】D
二．填空题（共8小题，满分32分，每小题4分）
9．（4分）已知 a 是锐角，sin（15°+α）＝，则a＝ 15° ．
【答案】见试题解答内容
10．（4分）在等腰三角形ABC中，AB＝AC，∠B＝50°，则∠A＝ 80 °．
【答案】80．
11．（4分）抛物线y＝4（x﹣2）2+1的顶点坐标是 （2，1） ．
【答案】（2，1）．
12．（4分）若x＝3是关于x的方程x2+3x﹣m2＝0的一个根，则m的值是 ±3 ．
【答案】±3．
13．（4分）一只盒子中有红球10个，白球6个，黑球a个，每个球除颜色外都相同，从中任取一个球，取得“红球”的概率与“不是红球”的概率相同，那么a的值是 4 ．
【答案】见试题解答内容
14．（4分）如图，在Rt△ABC中，∠C＝90°，∠B＝30°，AB＝8，以点C为圆心，CA的长为半径画弧，交AB于点D，则的长为 ．
【答案】．
15．（4分）如图是一张矩形纸片，点E是BC边上一点，将△ECD沿DE折叠，使点C落在矩形内的点C'处，当点C'恰好为矩形对角线中点时，则∠CBD＝ 30 °；当点C'落在对角线BD上，若A，C'，E共线，且AD＝2时，则CE的长为 3﹣ ．
【答案】30，3﹣．
16．（4分）如图，已知一次函数y＝ax+b（a≠0）的图象与反比例函数（k≠0，x＞0）的图象交于第一象限内点A，与x轴负半轴交于点B，过点A作AC⊥x轴于点C，D为AB的中点，线段CD交y轴于点E，连接BE．若△BEC的面积是6，则k的值是 12 .
【答案】12．
三．解答题（共9小题，满分86分）
17．（8分）（1）计算：；
（2）解方程：x2+6x+5＝0．
【答案】（1）2；
（2）x1＝﹣1，x2＝﹣5．
18．（8分）如图，AB＝CD，E，F分别为线段AC上的两点，DE⊥AC于E，BF⊥AC于F，且AE＝CF，BD交AC于点M．
（1）求证：DE＝BF；
（2）若BD＝6，求MB的长．
【答案】（1）见解析；
（2）3．
19．（8分）先化简，再求值：（﹣1）÷，其中m＝．
【答案】﹣，﹣1﹣．
20．（8分）已知BC是⊙O的直径，点D是BC延长线上一点，AB＝AD，AE是⊙O的弦，∠AEC＝30°．
（1）求证：直线AD是⊙O的切线；
（2）若AE⊥BC，垂足为M，⊙O的半径为10，求AE的长．
【答案】10．
21．（8分）2023年福建省全民健身运动会，以“我运动，我阳光、我运动，我快乐、我运动，我健康”为主题．活动项目有球类、帆船、游泳、田径、击剑等，某体育兴趣小组收集到了游泳、棒球、帆船、垫球四个项目的比赛规则，并制作了编号分别为A，B，C，D的4张卡片．如图，卡片除了图案和编号外无其他差别，现将它们洗匀后背面朝上放在桌子上．
（1）随机从中抽取一张卡片，抽到“帆船”的概率是 ；
（2）小康同学从中随机抽取一张（不放回），小亮同学从余下的3张卡片中再随机抽取一张，然后根据抽取的卡片讲述对应卡片上的比赛规则，请用列表或画树状图的方法求小康、小亮两人中有一人讲述“游泳”体育项目的比赛规则的概率．
【答案】（1）．
（2）．
22．（10分）如图，AC是菱形ABCD的对角线．
（1）尺规作图：将△ABC绕点A逆时针旋转得到△ADE，点B旋转后的对应点为D（保留作图痕迹，不写作法）；
（2）在（1）所作的图中，连接BD，CE．
①求证：△ABD～△ACE；
②若tan∠BAC＝，求cs∠DCE的值．
【答案】（1）作法、证明见解答；
（2）①证明见解答；
②cs∠DCE的值是．
23．（10分）根据以下素材，探索完成任务．
【答案】【任务1】，
【任务2】17.8．
24．（12分）在平面直角坐标系xOy中，抛物线y＝ax2+bx﹣3与x轴交于A（﹣1，0），B（3，0）两点，与y轴交于点C．
（1）求该抛物线的函数解析式；
（2）连接AC，BC，点D是直线BC下方抛物线上的一个的动点（不与B，C重合），
①求△BCD面积的最大值；
②若∠ACO+∠BCD＝∠ABC，求点D的坐标．
【答案】（1）y＝x2﹣2x﹣3；
（2）①△BCD面积的最大值为；
②D（，﹣）．
25．（14分）已知，四边形ABCD内接于⊙O，，点T在BC的延长线上．
（1）如图1，求证：CD平分∠ACT；
（2）如图2，若AC是⊙O的直径，BE平分∠ABC交CD延长线于E，交⊙O于F，连接AE，AF，DF．
①求∠AED的度数；
②若，△DEF的面积等于，求AC的长．
【答案】（2）①∠AED＝45°；
②．
如何设计警戒线之间的宽度
素材1

图1为某公园的抛物线型拱桥，图2是其横截面示意图，测得水面宽度AB＝24米，拱顶离水面的距离为CD＝4米．
素材2
拟在公园里投放游船供游客乘坐，载重最少时，游船的横截面如图3所示，漏出水面的船身为矩形，船顶为等腰三角形．如图3，测得相关数据如下：EF＝EK＝1.7米，FK＝3米，GH＝IJ＝1.26米，FG＝JK＝0.4米．
素材3
为确保安全，拟在石拱桥下面的P，Q两处设置航行警戒线，要求如下：
①游船底部HI在P，Q之间通行；
②当载重最少通过时，游船顶部E与拱桥的竖直距离至少为0.25米．
问题解决
任务1
确定拱桥形状
在图2中建立合适的直角坐标系，并求这条抛物线的解析式；
任务2
设计警戒线之间的宽度
求PQ的最大值．
如何设计警戒线之间的宽度
素材1

图1为某公园的抛物线型拱桥，图2是其横截面示意图，测得水面宽度AB＝24米，拱顶离水面的距离为CD＝4米．
素材2
拟在公园里投放游船供游客乘坐，载重最少时，游船的横截面如图3所示，漏出水面的船身为矩形，船顶为等腰三角形．如图3，测得相关数据如下：EF＝EK＝1.7米，FK＝3米，GH＝IJ＝1.26米，FG＝JK＝0.4米．
素材3
为确保安全，拟在石拱桥下面的P，Q两处设置航行警戒线，要求如下：
①游船底部HI在P，Q之间通行；
②当载重最少通过时，游船顶部E与拱桥的竖直距离至少为0.25米．
问题解决
任务1
确定拱桥形状
在图2中建立合适的直角坐标系，并求这条抛物线的解析式；
任务2
设计警戒线之间的宽度
求PQ的最大值．