专题18 二次函数与几何图形综合题（与角度问题）-备战2024年中考数学一轮复习重难题型（全国通用）

这是一份专题18 二次函数与几何图形综合题（与角度问题）-备战2024年中考数学一轮复习重难题型（全国通用），文件包含专题18二次函数与几何图形综合题与角度问题原卷版docx、专题18二次函数与几何图形综合题与角度问题解析版docx等2份试卷配套教学资源，其中试卷共72页， 欢迎下载使用。
2、学会运用数形结合思想。数形结合思想是指从几何直观的角度,利用几何图形的性质研究数量关系，寻求代数问题的解决方法（以形助数），或利用数量关系来研究几何图形的性质，解决几何问题（以数助形）的一种数学思想。
3、要学会抢得分点。一道中考数学压轴题解不出来，不等于“一点不懂、一点不会”，要将整道题目解题思路转化为得分点。
4、学会运用等价转换思想。在研究数学问题时，我们通常是将未知问题转化为已知的问题，将复杂的问题转化为简单的问题，将抽象的问题转化为具体的问题，将实际问题转化为数学问题。
5、学会运用分类讨论的思想。如果不注意对各种情况分类讨论，就有可能造成错解或漏解，纵观近几年的中考压轴题分类讨论思想解题已成为新的热点。
6、转化思想:体现在数学上也就是要把难的问题转化为简单的问题，把不熟悉的问题转化为熟悉的问题，把未知的问题转化为已知的问题。
专题18二次函数与几何图形综合题（与角度问题）
1．（2023·湖南常德·统考中考真题）如图，二次函数的图象与x轴交于，两点，与y轴交于点C，顶点为D．O为坐标原点，．

(1)求二次函数的表达式；
(2)求四边形的面积；
(3)P是抛物线上的一点，且在第一象限内，若，求P点的坐标．
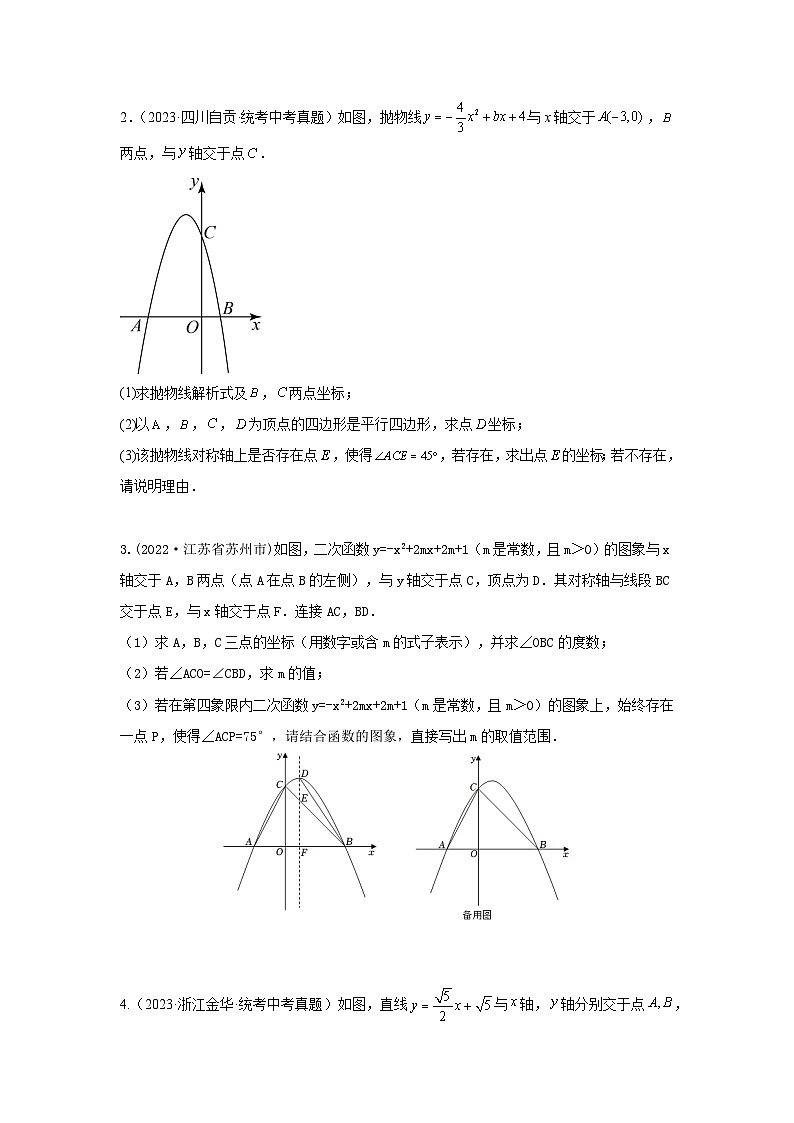
2．（2023·四川自贡·统考中考真题）如图，抛物线与x轴交于，两点，与轴交于点．

(1)求抛物线解析式及，两点坐标；
(2)以，，，为顶点的四边形是平行四边形，求点坐标；
(3)该抛物线对称轴上是否存在点，使得，若存在，求出点的坐标；若不存在，请说明理由．
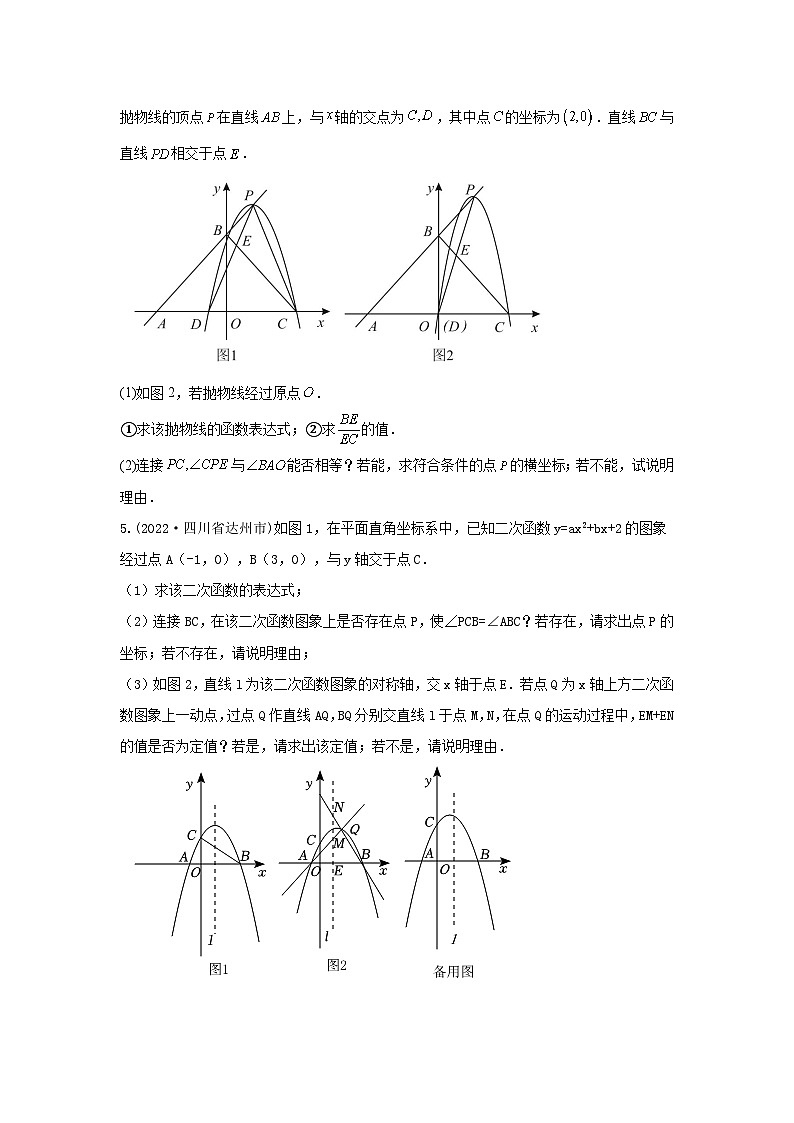
3.(2022·江苏省苏州市)如图，二次函数y=-x2+2mx+2m+1（m是常数，且m＞0）的图象与x轴交于A，B两点（点A在点B的左侧），与y轴交于点C，顶点为D．其对称轴与线段BC交于点E，与x轴交于点F．连接AC，BD．
（1）求A，B，C三点的坐标（用数字或含m的式子表示），并求∠OBC的度数；
（2）若∠ACO=∠CBD，求m的值；
（3）若在第四象限内二次函数y=-x2+2mx+2m+1（m是常数，且m＞0）的图象上，始终存在一点P，使得∠ACP=75°，请结合函数的图象，直接写出m的取值范围．
4.（2023·浙江金华·统考中考真题）如图，直线与轴，轴分别交于点，抛物线的顶点在直线上，与轴的交点为，其中点的坐标为．直线与直线相交于点．

(1)如图2，若抛物线经过原点．
①求该抛物线的函数表达式；②求的值．
(2)连接与能否相等？若能，求符合条件的点的横坐标；若不能，试说明理由．
5.(2022·四川省达州市)如图1，在平面直角坐标系中，已知二次函数y=ax2+bx+2的图象经过点A（-1，0），B（3，0），与y轴交于点C．
（1）求该二次函数的表达式；
（2）连接BC，在该二次函数图象上是否存在点P，使∠PCB=∠ABC？若存在，请求出点P的坐标；若不存在，请说明理由；
（3）如图2，直线l为该二次函数图象的对称轴，交x轴于点E．若点Q为x轴上方二次函数图象上一动点，过点Q作直线AQ，BQ分别交直线l于点M，N，在点Q的运动过程中，EM+EN的值是否为定值？若是，请求出该定值；若不是，请说明理由．
6.（2021·江苏连云港市·中考真题）如图，抛物线与x轴交于点A、B，与y轴交于点C，已知．
（1）求m的值和直线对应的函数表达式；
（2）P为抛物线上一点，若，请直接写出点P的坐标；
（3）Q为抛物线上一点，若，求点Q的坐标．
7．（2023·新疆·统考中考真题）【建立模型】(1)如图，点是线段上的一点，，，，垂足分别为，，，．求证：；
【类比迁移】(2)如图，一次函数的图象与轴交于点、与轴交于点，将线段绕点逆时针旋转得到、直线交轴于点．
①求点的坐标；
②求直线的解析式；
【拓展延伸】(3)如图，抛物线与轴交于，两点点在点的左侧，与轴交于点，已知点，，连接．抛物线上是否存在点，使得，若存在，求出点的横坐标．

8.（2021·四川自贡市·中考真题）如图，抛物线（其中）与x轴交于A、B两点，交y轴于点C．
（1）直接写出的度数和线段AB的长（用a表示）；
（2）若点D为的外心，且与的周长之比为，求此抛物线的解析式；
（3）在（2）的前提下，试探究抛物线上是否存在一点P，使得？若存在，求出点P的坐标；若不存在，请说明理由．
9．（2023·湖南岳阳·统考中考真题）已知抛物线与轴交于两点，交轴于点．

(1)请求出抛物线的表达式．
(2)如图1，在轴上有一点，点在抛物线上，点为坐标平面内一点，是否存在点使得四边形为正方形？若存在，请求出点的坐标；若不存在，请说明理由．
(3)如图2，将抛物线向右平移2个单位，得到抛物线，抛物线的顶点为，与轴正半轴交于点，抛物线上是否存在点，使得？若存在，请求出点的坐标；若不存在，请说明理由．
10.（2021·辽宁中考真题）已知函数，记该函数图像为G．
（1）当时，
①已知在该函数图像上，求n的值；
②当时，求函数G的最大值；
（2）当时，作直线与x轴交于点P，与函数G交于点Q，若时，求m的值；
（3）当时，设图像与x轴交于点A，与y轴交与点B，过B做交直线与点C，设点A的横坐标为a，C点的纵坐标为c，若，求m的值．
11．（2023·湖南郴州·统考中考真题）已知抛物线与轴相交于点，，与轴相交于点．
(1)求抛物线的表达式；
(2)如图1，点是抛物线的对称轴上的一个动点，当的周长最小时，求的值；
(3)如图2，取线段的中点，在抛物线上是否存在点，使？若存在，求出点的坐标；若不存在，请说明理由．
12．（2023·四川宜宾·统考中考真题）如图，抛物线与x轴交于点、，且经过点．

(1)求抛物线的表达式；
(2)在x轴上方的抛物线上任取一点N，射线、分别与抛物线的对称轴交于点P、Q，点Q关于x轴的对称点为，求的面积；
(3)点M是y轴上一动点，当最大时，求M的坐标．
13.（2021·湖北中考真题）在平面直角坐标系中，抛物线与轴交于点和点，与轴交于点，顶点的坐标为．
（1）直接写出抛物线的解析式；
（2）如图1，若点在抛物线上且满足，求点的坐标；
（3）如图2，是直线上一个动点，过点作轴交抛物线于点，是直线上一个动点，当为等腰直角三角形时，直接写出此时点及其对应点的坐标
14．（2023·湖北十堰·统考中考真题）已知抛物线过点和点，与轴交于点．

(1)求抛物线的解析式；
(2)如图1，连接，点在线段上（与点不重合），点是的中点，连接，过点作交于点，连接，当面积是面积的3倍时，求点的坐标；
(3)如图2，点是抛物线上对称轴右侧的点，是轴正半轴上的动点，若线段上存在点（与点不重合），使得，求的取值范围．
15.（2021·四川中考真题）如图，在平面直角坐标系中，已知抛物线经过点和点．
（1）求这条抛物线所对应的函数表达式；
（2）点为该抛物线上一点（不与点重合），直线将的面积分成2：1两部分，求点的坐标；
（3）点从点出发，以每秒1个单位的速度沿轴移动，运动时间为秒，当时，求的值．
16.（2021·山东中考真题）如图，在平面直角坐标系中，直线与轴交于点，与轴交于点，抛物线经过坐标原点和点，顶点为点．
（1）求抛物线的关系式及点的坐标；
（2）点是直线下方的抛物线上一动点，连接，，当的面积等于时，求点的坐标；
（3）将直线向下平移，得到过点的直线，且与轴负半轴交于点，取点，连接，求证：．