第03讲 正比例函数与一次函数（考点精析+真题精讲）-备战2024年中考数学一轮复习考点研究（全国通用）

这是一份第03讲 正比例函数与一次函数（考点精析+真题精讲）-备战2024年中考数学一轮复习考点研究（全国通用），文件包含第三讲正比例函数与一次函数考点精析+真题精讲原卷版docx、第三讲正比例函数与一次函数考点精析+真题精讲解析版docx等2份试卷配套教学资源，其中试卷共27页， 欢迎下载使用。

2、学会运用数形结合思想。数形结合思想是指从几何直观的角度,利用几何图形的性质研究数量关系，寻求代数问题的解决方法（以形助数），或利用数量关系来研究几何图形的性质，解决几何问题（以数助形）的一种数学思想。
3、要学会抢得分点。一道中考数学压轴题解不出来，不等于“一点不懂、一点不会”，要将整道题目解题思路转化为得分点。
4、学会运用等价转换思想。在研究数学问题时，我们通常是将未知问题转化为已知的问题，将复杂的问题转化为简单的问题，将抽象的问题转化为具体的问题，将实际问题转化为数学问题。
5、学会运用分类讨论的思想。如果不注意对各种情况分类讨论，就有可能造成错解或漏解，纵观近几年的中考压轴题分类讨论思想解题已成为新的热点。
6、转化思想:体现在数学上也就是要把难的问题转化为简单的问题，把不熟悉的问题转化为熟悉的问题，把未知的问题转化为已知的问题。
备战2024中考数学一轮复习
第3讲正比例函数与一次函数
№考向解读
➊考点精析
➋真题精讲
➌题型突破
➍专题精练
第三章函数
第3讲正比例函数与一次函数
→➊考点精析←
→➋真题精讲←
考向一 一次函数和正比例函数的定义
考向二 一次函数的图象及性质
考向三 用待定系数法确定一次函数的解析式
第3讲正比例函数与一次函数
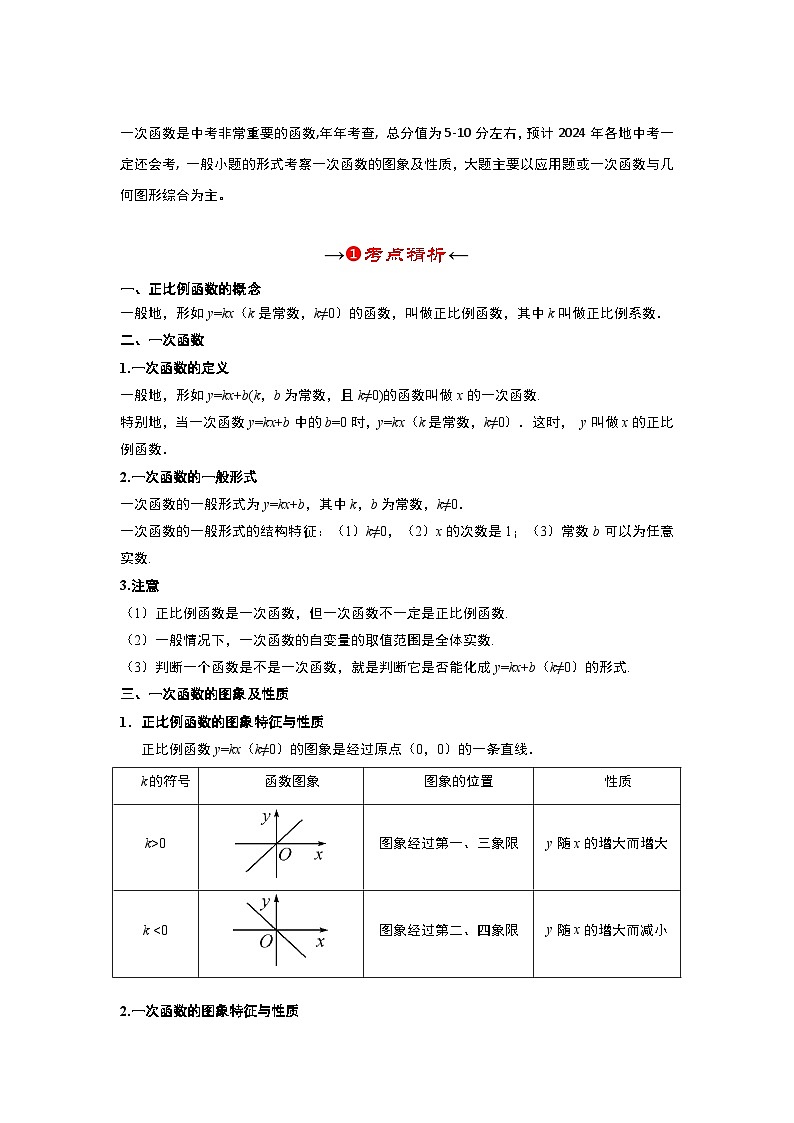
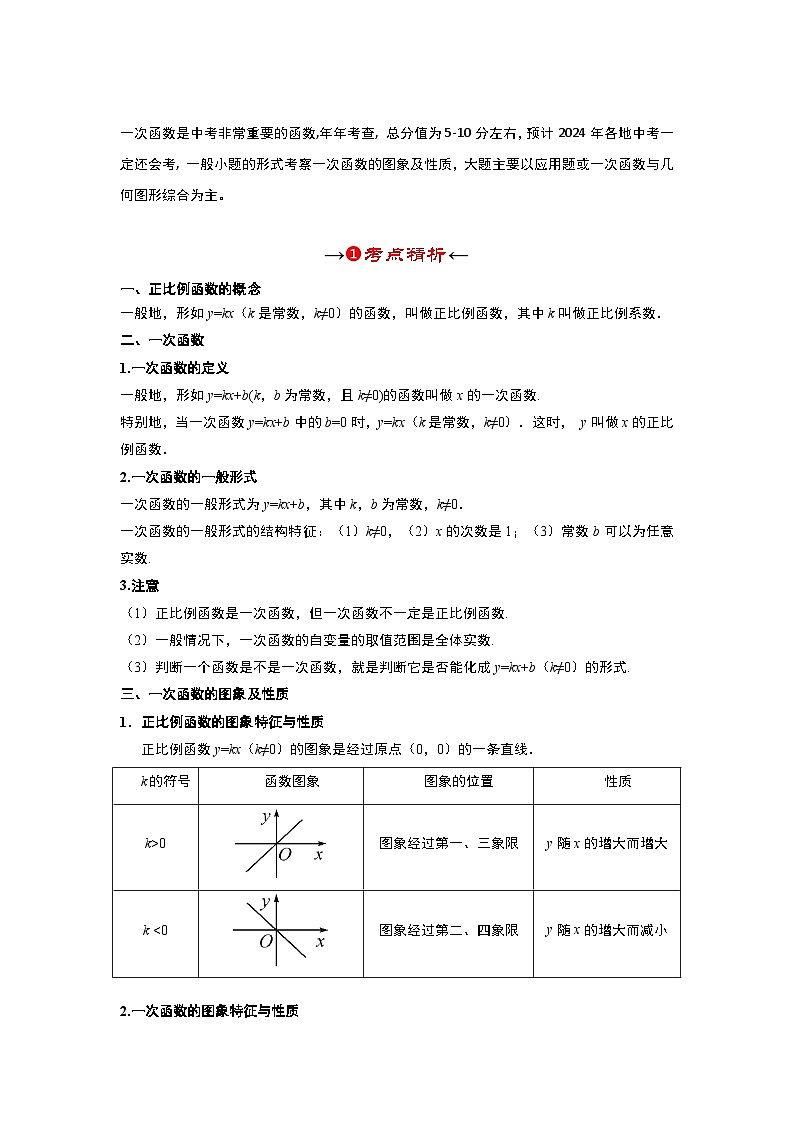
一次函数是中考非常重要的函数,年年考查, 总分值为5-10分左右，预计2024年各地中考一定还会考, 一般小题的形式考察一次函数的图象及性质，大题主要以应用题或一次函数与几何图形综合为主。
→➊考点精析←
一、正比例函数的概念
一般地，形如y=kx（k是常数，k≠0）的函数，叫做正比例函数，其中k叫做正比例系数．
二、一次函数
1.一次函数的定义
一般地，形如y=kx+b(k，b为常数，且k≠0)的函数叫做x的一次函数.
特别地，当一次函数y=kx+b中的b=0时，y=kx（k是常数，k≠0）．这时， y叫做x的正比例函数．
2.一次函数的一般形式
一次函数的一般形式为y=kx+b，其中k，b为常数，k≠0．
一次函数的一般形式的结构特征：（1）k≠0，（2）x的次数是1；（3）常数b可以为任意实数.
3.注意
（1）正比例函数是一次函数，但一次函数不一定是正比例函数.
（2）一般情况下，一次函数的自变量的取值范围是全体实数.
（3）判断一个函数是不是一次函数，就是判断它是否能化成y=kx+b（k≠0）的形式.
三、一次函数的图象及性质
1．正比例函数的图象特征与性质
正比例函数y=kx（k≠0）的图象是经过原点（0，0）的一条直线．
2.一次函数的图象特征与性质
（1）一次函数的图象
（2）一次函数的性质
3.k，b的符号与直线y=kx+b（k≠0）的关系
在直线y=kx+b（k≠0）中，令y=0，则x=- ，即直线y=kx+b与x轴交于（–，0）．
①当–>0时，即k，b异号时，直线与x轴交于正半轴．
②当–=0，即b=0时，直线经过原点．
③当–<0，即k，b同号时，直线与x轴交于负半轴．
4.两直线y=k1x+b1（k1≠0）与y=k2x+b2（k2≠0）的位置关系：
①当k1=k2，b1≠b2，两直线平行； ②当k1=k2，b1=b2，两直线重合；
③当k1≠k2，b1=b2，两直线交于y轴上一点； ④当k1·k2=–1时，两直线垂直．
四、待定系数法
1．定义：先设出函数解析式，再根据条件确定解析式中未知数的系数，从而得出函数解析式的方法叫做待定系数法．
2．待定系数法求正比例函数解析式的一般步骤
（1）设含有待定系数的函数解析式为y=kx（k≠0）．
（2）把已知条件（自变量与函数的对应值）代入解析式，得到关于系数k的一元一次方程．
（3）解方程，求出待定系数k．
（4）将求得的待定系数k的值代入解析式．
3．待定系数法求一次函数解析式的一般步骤
（1）设出含有待定系数k、b的函数解析式y=kx+b．
（2）把两个已知条件（自变量与函数的对应值）代入解析式，得到关于系数k，b的二元一次方程组．
（3）解二元一次方程组，求出k，b．
（4）将求得的k，b的值代入解析式．
五、一次函数与正比例函数的区别与联系
→➋真题精讲←
考向一 一次函数和正比例函数的定义
1．正比例函数是特殊的一次函数．
2．正比例函数解析式y=kx（k≠0）的结构特征：①k≠0；②x的次数是1．
1．（2020·四川中考真题）已知函数，当函数值为3时，自变量x的值为（ ）
A．﹣2B．﹣C．﹣2或﹣D．﹣2或﹣
【答案】A
【分析】根据分段函数的解析式分别计算，即可得出结论．
【解析】解：若x＜2，当y=3时，﹣x+1=3，解得：x=﹣2；
若x≥2，当y=3时，﹣=3，解得：x=﹣，不合题意舍去；∴x=﹣2，故选：A．
【点睛】本题考查了反比例函数的性质、一次函数的图象上点的坐标特征；根据分段函数进行分段求解是解题的关键．
2．（2020·四川成都市·九年级二模）下列函数关系式：（1）y＝﹣x；（2）y＝x﹣1；（3）y＝；（4）y＝x2，其中一次函数的个数是（ ）
A．1B．2C．3D．4
【答案】B
【分析】根据一次函数的定义条件进行逐一分析即可．
【详解】解：（1）y＝﹣x是正比例函数，是特殊的一次函数，故正确；
（2）y＝x﹣1符合一次函数的定义，故正确；（3）y＝属于反比例函数，故错误；
（4）y＝x2属于二次函数，故错误．综上所述，一次函数的个数是2个．故选：B．
【点睛】本题主要考查了一次函数的定义．本题主要考查了一次函数的定义，一次函数y=kx+b的定义条件是：k、b为常数，k≠0，自变量次数为1．
考向二 一次函数的图象及性质
1．通常画正比例函数y=kx（k≠0）的图象时只需取一点（1，k），然后过原点和这一点画直线．
2．当k>0时，函数y=kx（k≠0）的图象从左向右，呈上升趋势；当k<0时，函数y=kx（k≠0）的图象从左向右，呈下降趋势．
3．正比例函数y=kx中，|k|越大，直线y=kx越靠近y轴；|k|越小，直线y=kx越靠近x轴．
4．一次函数图象的位置和函数值y的增减性完全由b和比例系数k的符号决定．
3．（2023·四川乐山·统考中考真题）下列各点在函数图象上的是（ ）
A．B．C．D．
【答案】D
【分析】根据一次函数图象上点的坐标特征，将选项中的各点分别代入函数解析式，进行计算即可得到答案．
【详解】解：一次函数图象上的点都在函数图象上，
函数图象上的点都满足函数解析式，
A.当时，，故本选项错误，不符合题意；
B.当时，，故本选项错误，不符合题意；
C.当时，，故本选项错误，不符合题意；
D.当时，，故本选项正确，符合题意；
故选：D．
【点睛】本题主要考查了一次函数图象上点的坐标特征，熟练掌握一次函数图象上的点都在函数图象上，是解题的关键．
4．（2023·甘肃武威·统考中考真题）若直线（是常数，）经过第一、第三象限，则的值可为（ ）
A．B．C．D．2
【答案】D
【分析】通过经过的象限判断比例系数k的取值范围，进而得出答案．
【详解】∵直线（是常数，）经过第一、第三象限，
∴，
∴的值可为2，
故选：D．
【点睛】本题考查正比例函数的图象与性质，熟记比例系数与图象经过的象限之间的关系是解题的关键．
5．（2020·山东济南·中考真题）若m﹣2，则一次函数的图象可能是（ ）
A． B． C． D．
【答案】D
【分析】由m＜﹣2得出m+1＜0，1﹣m＞0，进而利用一次函数的性质解答即可．
【解析】解：∵m＜﹣2，∴m+1＜0，1﹣m＞0，
所以一次函数的图象经过一，二，四象限，故选：D．
【点睛】本题考查的是一次函数的图像与性质，不等式的基本性质，掌握一次函数中的对函数图像的影响是解题的关键 ．
6．（2023·内蒙古·统考中考真题）在平面直角坐标系中，将正比例函数的图象向右平移3个单位长度得到一次函数的图象，则该一次函数的解析式为（ ）
A．B．C．D．
【答案】B
【分析】根据一次函数的平移规律求解即可．
【详解】解：正比例函数的图象向右平移3个单位长度得：
，
故选：B．
【点睛】题目主要考查一次函数的平移，熟练掌握平移规律是解题关键．
7．（2023·内蒙古通辽·统考中考真题）在平面直角坐标系中，一次函数的图象是（ ）
A． B．
C． D．
【答案】D
【分析】依据一次函数的图象经过点和，即可得到一次函数的图象经过一、三、四象限．
【详解】解：一次函数中，令，则；令，则，
∴一次函数的图象经过点和，
∴一次函数的图象经过一、三、四象限，
故选：D．
【点睛】本题主要考查了一次函数的图象，一次函数的图象是与坐标轴不平行的一条直线．
8.（2023·新疆·统考中考真题）一次函数的图象不经过（ ）
A．第一象限B．第二象限C．第三象限D．第四象限
【答案】D
【分析】根据即可求解．
【详解】解：∵一次函数中，
∴一次函数的图象不经过第四象限，
故选：D．
【点睛】本题考查了一次函数的性质，熟练掌握一次函数的性质是解题的关键．
9．（2023·甘肃兰州·统考中考真题）一次函数的函数值y随x的增大而减小，当时，y的值可以是（ ）
A．2B．1C．－1D．－2
【答案】D
【分析】根据一次函数的增减性可得k的取值范围，再把代入函数，从而判断函数值y的取值．
【详解】∵一次函数的函数值y随x的增大而减小
∴
∴当时，
故选：D.
【点睛】本题考查一次函数的性质，不等式的性质，熟悉一次函数的性质是解题的关键．
10．（2023·浙江温州·统考中考真题）如图，在直角坐标系中，点在直线上，过点A的直线交y轴于点．

(1)求m的值和直线的函数表达式．
(2)若点在线段上，点在直线上，求的最大值．
【答案】(1)，；(2)
【分析】（1）把点A的坐标代入直线解析式可求解m，然后设直线的函数解析式为，进而根据待定系数法可进行求解函数解析式；
（2）由（1）及题意易得，，则有，然后根据一次函数的性质可进行求解．
【详解】（1）解：把点代入，得．
设直线的函数表达式为，把点，代入得
，解得，
∴直线的函数表达式为．
（2）解：∵点在线段上，点在直线上，
∴，，
∴．
∵，
∴的值随的增大而减小，
∴当时，的最大值为．
【点睛】本题主要考查一次函数的图象与性质，熟练掌握一次函数的图象与性质是解题的关键．
考向三 用待定系数法确定一次函数的解析式
运用待定系数法求一次函数解析式的步骤可简单记为：一设，二代，三解，四回代．
11．（2023·内蒙古通辽·统考中考真题）如图，在平面直角坐标系中，已知点，点，以点P为中心，把点A按逆时针方向旋转得到点B，在，，，四个点中，直线经过的点是（ ）

A．B．C．D．
【答案】B
【分析】根据含角的直角三角形的性质可得，利用待定系数法可得直线的解析式，依次将四个点的一个坐标代入中可解答．
【详解】解：∵点，点，

∴轴，，
由旋转得：，
如图，过点B作轴于C，
∴，
∴，
∴），
设直线的解析式为：，
则，
∴，
∴直线的解析式为：，
当时，，
∴点不在直线上，
当时，，
∴在直线上，
当时，
∴不在直线上，
当时，，
∴不在直线上．
故选：B．
【点睛】本题考查的是图形旋转变换，待定系数法求一次函数的解析式，确定点B的坐标是解本题的关键．
12．（2023·江苏苏州·统考中考真题）已知一次函数的图象经过点和，则________________．
【答案】
【分析】把点和代入，可得，再整体代入求值即可．
【详解】解：∵一次函数的图象经过点和，
∴，即，
∴；
故答案为：
【点睛】本题考查的是一次函数的性质，利用待定系数法求解一次函数的解析式，利用平方差公式分解因式，熟练的利用平方差公式求解代数式的值是解本题的关键．
14．已知函数y＝(2m+1)x+m﹣3；
(1)若函数图象经过原点，求m的值；
(2)若函数图象在y轴的截距为﹣2，求m的值；
(3)若函数的图象平行直线y＝3x﹣3，求m的值；
(4)若这个函数是一次函数，且y随着x的增大而减小，求m的取值范围．
【答案】(1)m＝3；(2)m＝1；(3)m＝1；(4)m＜﹣．
【分析】
(1)根据函数图象经过原点可得m﹣3＝0，且2m+1≠0，再解即可；
(2)根据题意可得m﹣3＝﹣2，解方程即可；
(3)根据两函数图象平行，k值相等可得2m+1＝3；
(4)根据一次函数的性质可得2m+1＜0，再解不等式即可．
【详解】
解：(1)∵函数图象经过原点，
∴m﹣3＝0，且2m+1≠0，
解得：m＝3；
(2)∵函数图象在y轴的截距为﹣2，
∴m﹣3＝﹣2，且2m+1≠0，
解得：m＝1；
(3)∵函数的图象平行直线y＝3x﹣3，
∴2m+1＝3，
解得：m＝1；
(4)∵y随着x的增大而减小，
∴2m+1＜0，
解得：m＜﹣．
【点睛】
此题主要考查了一次函数的性质，关键是掌握与y轴的交点就是y＝kx+b中，b的值，k＞0，y随x的增大而增大，函数从左到右上升；k＜0，y随x的增大而减小，函数从左到右下降．
14．若与成正比例，且当时，.
（1）求与的函数关系式
（2）如果点在该函数图象上，求的值.
【答案】（1）y=x+3；（2）m=2.
【分析】
（1）设y-1=k（x+2），把x=2，y=-5代入求出k的值，进而可得出y与x的函数关系式；
（2）直接把点（m，5）代入（1）中一次函数的解析式即可．
【详解】
解：（1）设 （）
当x＝2时，y＝5
5-1=(2+2)k
∴k=1
当K＝10时
y-1=x+2
y=x+3
（2）当点（m，5）在该函数图象上
∴5=m+3
∴m=2
【点睛】
本题考查的是待定系数法求一次函数的解析式，熟知待定系数法求一次函数解析式的一般步骤是解答此题的关键．
15．若函数y＝（m+1）x+m2﹣1是正比例函数．
（1）求该函数的表达式．
（2）将该函数图象沿y轴向上或者向下平移，使其经过（1，﹣2），求平移的方向与距离．
【答案】（1）y＝2x；（2）沿y轴向下平移4个单位．
【分析】
（1）根据正比例函数的定义可得一个关于m的等式，求得m值代入函数解析式即可得；
（2）根据函数解析式可设平移后的函数解析式为，将代入求得b值，再根据平移后的函数解析式即可得.
【详解】
（1）根据题意得且，
解得，
所以该函数的表达式为；
（2）设平移后的函数解析式为，
将代入得，
解得，
则平移后的函数解析式为，
所以函数的图象是沿y轴向下平移4个单位，使其经过.
【点睛】
本题考查了正比例函数的定义、待定系数法求函数解析式、以及函数图象的平移，掌握正比例函数的定义是解题关键.
k的符号
函数图象
图象的位置
性质
k>0
图象经过第一、三象限
y随x的增大而增大
k <0
图象经过第二、四象限
y随x的增大而减小
一次函数的图象
一次函数y=kx+b(k≠0)的图象是经过点(0，b)和(-，0)的一条直线
图象关系
一次函数y=kx+b(k≠0)的图象可由正比例函数y=kx(k≠0)的图象平移得到；b>0，向上平移b个单位长度；b<0，向下平移|b|个单位长度
图象确定
因为一次函数的图象是一条直线，由两点确定一条直线可知画一次函数图象时，只要取两点即可
函数
字母取值
图象
经过的象限
函数性质
y=kx+b
(k≠0)
k>0，b>0
一、二、三
y随x的增大而增大
k>0，b<0
一、三、四
y=kx+b
(k≠0)
k<0，b>0
一、二、四
y随x的增大而减小
k<0，b<0
二、三、四
正比例函数
一次函数
区别
一般形式
y=kx+b（k是常数，且k≠0）
y=kx+b（k，b是常数，且k≠0）
图象
经过原点的一条直线
一条直线
k，b符号的作用
k的符号决定其增减性，同时决定直线所经过的象限
k的符号决定其增减性；b的符号决定直线与y轴的交点位置；k，b的符号共同决定直线经过的象限
求解析式的条件
只需要一对x，y的对应值或一个点的坐标
需要两对x，y的对应值或两个点的坐标
联系
比例函数是特殊的一次函数．
②正比例函数图象与一次函数图象的画法一样，都是过两点画直线，但画一次函数的图象需取两个不同的点，而画正比例函数的图象只要取一个不同于原点的点即可．
③一次函数y=kx+b（k≠0）的图象可以看作是正比例函数y=kx（k≠0）的图象沿y轴向上（b>0）或向下（b<0）平移|b|个单位长度得到的．由此可知直线y=kx+b（k≠0，b≠0）与直线y=kx（k≠0）平行．
④一次函数与正比例函数有着共同的性质：
a．当k>0时，y的值随x值的增大而增大；b．当k<0时，y的值随x值的增大而减小．