专题33锐角三角函数函数（优选真题60道）-三年（2021-2023）中考数学真题分项汇编【全国通用】

这是一份专题33锐角三角函数函数（优选真题60道）-三年（2021-2023）中考数学真题分项汇编【全国通用】，文件包含专题33锐角三角函数函数优选真题60道-学易金卷三年2021-2023中考数学真题分项汇编全国通用原卷版docx、专题33锐角三角函数函数优选真题60道-学易金卷三年2021-2023中考数学真题分项汇编全国通用解析版docx等2份试卷配套教学资源，其中试卷共83页， 欢迎下载使用。

1．（2022•天津）tan45°的值等于（ ）
A．2B．1C．22D．33
【分析】根据特殊角的三角函数值，进行计算即可解答．
【解答】解：tan45°的值等于1，
故选：B．
【点评】本题考查了特殊角的三角函数值，熟练掌握特殊角的三角函数值是解题的关键．
2．（2023•日照）日照灯塔是日照海滨港口城市的标志性建筑之一，主要为日照近海及进出日照港的船舶提供导航服务．数学小组的同学要测量灯塔的高度，如图所示，在点B处测得灯塔最高点A的仰角∠ABD＝45°，再沿BD方向前进至C处测得最高点A的仰角∠ACD＝60°，BC＝15.3m，则灯塔的高度AD大约是（ ）（结果精确到1m，参考数据：2≈1.41，3≈1.73）
A．31mB．36mC．42mD．53m
【分析】根据题意可得：AD⊥BD，然后设CD＝xm，则BD＝（x+15.3）m，在Rt△ABD中，利用锐角三角函数的定义求出AD的长，再在Rt△ACD中，利用锐角三角函数的定义求出AD的长，从而列出关于x的方程，进行计算即可解答．
【解答】解：由题意得：AD⊥BD，
设CD＝xm，
∵BC＝15.3m，
∴BD＝BC+CD＝（x+15.3）m，
在Rt△ABD中，∠ABD＝45°，
∴AD＝BD•tan45°＝（x+15.3）m，
在Rt△ACD中，∠ACD＝60°，
∴AD＝CD•tan60°=3x（m），
∴3x＝（x+15.3），
解得：x≈21.0，
∴AD＝x+15.3≈36（m），
∴灯塔的高度AD大约是36m，
故选：B．
【点评】本题考查了解直角三角形的应用﹣仰角俯角问题，熟练掌握锐角三角函数的定义是解题的关键．
3．（2023•威海）常言道：失之毫厘，谬以千里．当人们向太空发射火箭或者描述星际位置时，需要非常准确的数据．1″的角真的很小．把整个圆等分成360份，每份这样的弧所对的圆心角的度数是1°．1°＝60′＝3600″．若一个等腰三角形的腰长为1千米，底边长为4.848毫米，则其顶角的度数就是1″．太阳到地球的平均距离大约为1.5×108千米．若以太阳到地球的平均距离为腰长，则顶角为1″的等腰三角形底边长为（ ）
A．24.24千米B．72.72千米C．242.4千米D．727.2千米
【分析】根据题意列方程求解即可．
【解答】解：设等腰三角形底边长为x毫米，由题意得，
14.848=1.5×108x，
解得x＝7.272×108，
7.272×108毫米＝727.2千米，
故选：D．
【点评】本题考查科学记数法，等腰三角形的性质，理解题意是正确解答的前提．
4．（2023•长春）学校开放日即将来临，负责布置的林老师打算从学校图书馆的顶楼拉出一条彩旗绳AB到地面，如图所示．已知彩旗绳与地面形成25°角（即∠BAC＝25°），彩旗绳固定在地面的位置与图书馆相距32米（即AC＝32米），则彩旗绳AB的长度为（ ）
A．32sin25°米B．32cs25°米C．32sin25°米D．32cs25°米
【分析】根据直角三角形的边角关系进行解答即可．
【解答】解：如图，由题意得，AC＝32m，∠A＝25°，
在Rt△ABC中，
∵csA=ACAB，
∴AB=ACcsA=32cs25°（m），
故选：D．
【点评】本题考查解直角三角形的应用，掌握直角三角形的边角关系是正确解答的前提．
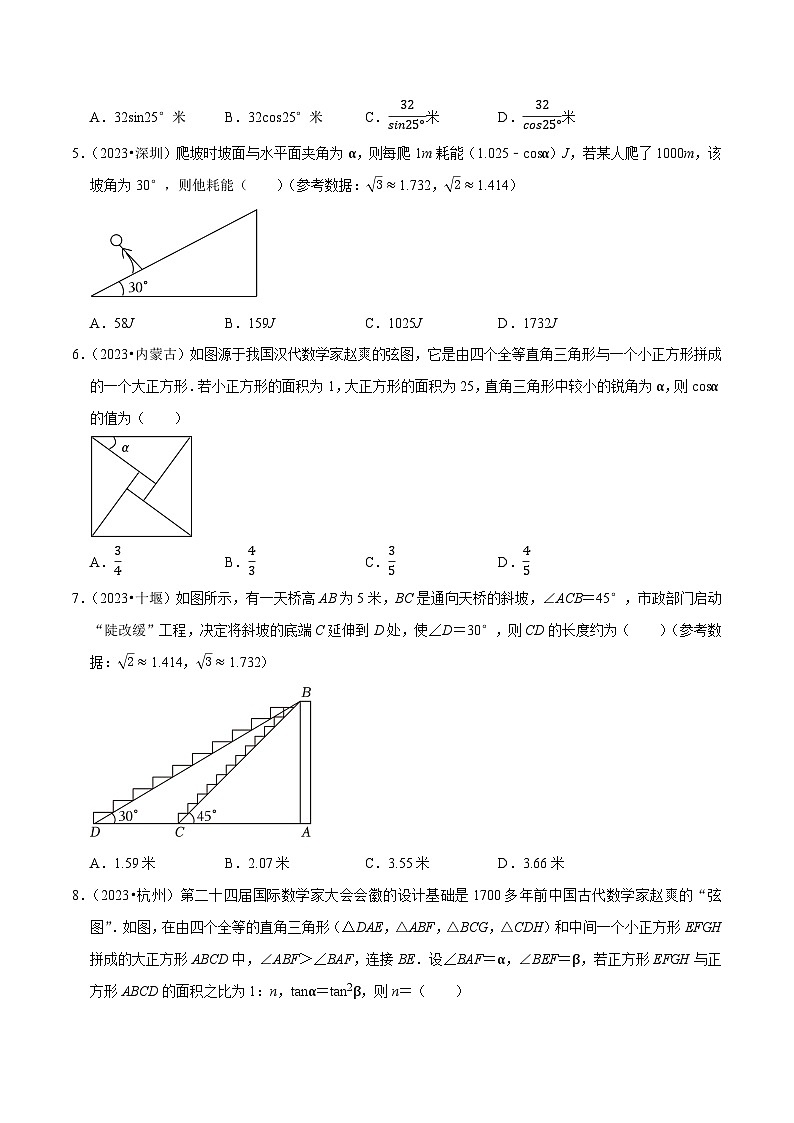
5．（2023•深圳）爬坡时坡面与水平面夹角为α，则每爬1m耗能（1.025﹣csα）J，若某人爬了1000m，该坡角为30°，则他耗能（ ）（参考数据：3≈1.732，2≈1.414）
A．58JB．159JC．1025JD．1732J
【分析】根据题意可得：他耗能＝1000×（1.025﹣cs30°），进行计算即可解答．
【解答】解：由题意得：
某人爬了1000m，该坡角为30°，则他耗能＝1000×（1.025﹣cs30°）＝1000×（1.025−32）≈159（J），
故选：B．
【点评】本题考查了解直角三角形的应用﹣坡度坡角问题，准确熟练地进行计算是解题的关键．
6．（2023•内蒙古）如图源于我国汉代数学家赵爽的弦图，它是由四个全等直角三角形与一个小正方形拼成的一个大正方形．若小正方形的面积为1，大正方形的面积为25，直角三角形中较小的锐角为α，则csα的值为（ ）
A．34B．43C．35D．45
【分析】首先根据两个正方形的面积分别求出两个正方形的边长，然后结合题意进一步设直角三角形较短的直角边为a，则较长的直角边为a+1，再利用勾股定理得到关于a的方程，解方程可求出直角三角形的两个个直角边的边长，最后根据锐角三角函数的定义可求出csα的值．
【解答】解：∵小正方形的面积为1，大正方形的面积为25，
∴小正方形的边长为 1，大正方形的边长为5，
设直角三角形中较短的直角边为a，则较长的直角边是a+1，其中a＞0，
由勾股定理得：a2+（a+1）2＝52，
整理得：a2+a﹣12＝0
解得：a1＝3，a2＝﹣4（不合题意，舍去）．
∴a+1＝4，
∴csα=45．
故选：D．
【点评】此题主要考查了锐角三角函数，勾股定理等，解答此题的关键是准确识图，熟练掌握锐角三角函数的定义，难点是设置适当的未知数，利用勾股定理构造方程求出三角形的边．
7．（2023•十堰）如图所示，有一天桥高AB为5米，BC是通向天桥的斜坡，∠ACB＝45°，市政部门启动“陡改缓”工程，决定将斜坡的底端C延伸到D处，使∠D＝30°，则CD的长度约为（ ）（参考数据：2≈1.414，3≈1.732）
A．1.59米B．2.07米C．3.55米D．3.66米
【分析】由∠BAC＝90°，∠ACB＝45°，得∠ABC＝∠ACB＝45°，则AC＝AB＝5米，由∠BAD＝90°，∠D＝30°，得∠ABD＝60°，则ADAB=tan60°=3，所以AD=3AB，则CD＝AD﹣AC=3AB﹣AC≈3.66米，于是得到问题的答案．
【解答】解：在Rt△ABC中，∠BAC＝90°，∠ACB＝45°，
∴∠ABC＝∠ACB＝45°，
∴AC＝AB＝5米，
在Rt△ABD中，∠BAD＝90°，∠D＝30°，
∴∠ABD＝60°，
∴ADAB=tan∠ABD＝tan60°=3，
∴AD=3AB，
∴CD＝AD﹣AC=3AB﹣AC≈1.732×5﹣5≈3.66（米），
∴CD的长度约为3.66米，
故选：D．
【点评】此题重点考查直角三角形的两个锐角互余、等腰直角三角形的判定、锐角三角函数与解直角三角形等知识，推导出AD=3AB是解题的关键．
8．（2023•杭州）第二十四届国际数学家大会会徽的设计基础是1700多年前中国古代数学家赵爽的“弦图”．如图，在由四个全等的直角三角形（△DAE，△ABF，△BCG，△CDH）和中间一个小正方形EFGH拼成的大正方形ABCD中，∠ABF＞∠BAF，连接BE．设∠BAF＝α，∠BEF＝β，若正方形EFGH与正方形ABCD的面积之比为1：n，tanα＝tan2β，则n＝（ ）
A．5B．4C．3D．2
【分析】设AE＝a，DE＝b，则BF＝a，AF＝b，解直角三角形可得ab=(ab−a)2，化简可得（b﹣a）2＝ab，a2+b2＝3ab，结合勾股定理及正方形的面积公式可求得S正方形EFGH；S正方形ABCD＝1：3，进而可求解n的值．
【解答】解：设AE＝a，DE＝b，则BF＝a，AF＝b，
∵tanα=ab，tanβ=ab−a，tanα＝tan2β，
∴ab=(ab−a)2，
∴（b﹣a）2＝ab，
∴a2+b2＝3ab，
∵a2+b2＝AD2＝S正方形ABCD，（b﹣a）2＝S正方形EFGH，
∴S正方形EFGH：S正方形ABCD＝ab：3ab＝1：3，
∵S正方形EFGH：S正方形ABCD＝1：n，
∴n＝3．
故选：C．
【点评】本题主要考查勾股定理的证明，解直角三角形的应用，利用解直角三角形求得（b﹣a）2＝ab，a2+b2＝3ab是解题的关键．
9．（2023•南充）如图，小兵同学从A处出发向正东方向走x米到达B处，再向正北方向走到C处，已知∠BAC＝α，则A，C两处相距（ ）
A．xsinα米B．xcsα米C．x•sinα米D．x•csα米
【分析】根据题意可得：BC⊥AB，然后在Rt△ABC中，利用锐角三角函数的定义求出AC的长，即可解答．
【解答】解：由题意得：BC⊥AB，
在Rt△ABC中，∠CAB＝α，AB＝x米，
∴AC=ABcsα=xcsα（米），
∴A，C两处相距xcsα米，
故选：B．
【点评】本题考查了解直角三角形的应用，熟练掌握锐角三角函数的定义是解题的关键．
10．（2023•自贡）如图，分别经过原点O和点A（4，0）的动直线a，b夹角∠OBA＝30°，点M是OB中点，连接AM，则sin∠OAM的最大值是（ ）
A．3+66B．32C．63D．56
【分析】作△AOB的外接圆⊙T，连接OT，TA，TB，取OT的中点K，连接KM．证明KM=12TB＝2，推出点M在以K为圆心，2为半径的圆上运动，当AM与⊙K相切时，∠OAM的值最大，此时sin∠OAM的值最大．
【解答】解：作△AOB的外接圆⊙T，连接OT，TA，TB，取OT的中点K，连接KM．
∵∠ATO＝2∠ABO＝60°，TO＝TA，
∴△OAT是等边三角形，
∵A（4，0），
∴TO＝TA＝TB＝4，
∵OK＝KT，OM＝MB，
∴KM=12TB＝2，
∴点M在以K为圆心，2为半径的圆上运动，
当AM与⊙K相切时，∠OAM的值最大，此时sin∠OAM的值最大，
∵△OTA是等边三角形，OK＝KT，
∴AK⊥OT，
∴AK=OA2−OK2=42−22=23，
∵AM是切线，KM是半径，
∴AM⊥KM，
∴AM=AK2−MK2=(23)2−22=22，
过点M作ML⊥OA于点L，KR⊥OA于点R，MP⊥RK于点P．
∵∠PML＝∠AMK＝90°，
∴∠PMK＝∠LMA，
∵∠P＝∠MLA＝90°，
∴△MPK∽△MLA，
∴MPML=PKAL=MKAM=222=12，
设PK＝x，PM＝y，则有ML=2y，AL=2x，
∴2y=3+x①，y＝3−2x，
解得，x=32−33，y=3+63，
∴ML=2y=32+233，
∴sin∠OAM=MLAM=32+23322=3+66．
故选：A．
【点评】本题考查解直角三角形，相似三角形的判定和性质，三角形的外接圆，三角形中位线定理等知识，解题的关键是学会添加常用辅助线，构造相似三角形解决问题．
11．（2022•金华）一配电房示意图如图所示，它是一个轴对称图形．已知BC＝6m，∠ABC＝α，则房顶A离地面EF的高度为（ ）
A．（4+3sinα）mB．（4+3tanα）mC．（4+3sinα）mD．（4+3tanα）m
【分析】过点A作AD⊥BC于点D，利用直角三角形的边角关系定理求得AD，．用AD+BE即可表示出房顶A离地面EF的高度．
【解答】解：过点A作AD⊥BC于点D，如图，
∵它是一个轴对称图形，
∴AB＝AC，
∵AD⊥BC，
∴BD=12BC＝3m，
在Rt△ADB中，
∵tan∠ABC=ADBD，
∴AD＝BD•tanα＝3tanαm．
∴房顶A离地面EF的高度＝AD+BE＝（4+3tanα）m，
故选：B．
【点评】本题主要考查了解直角三角形的意义，轴对称的性质，等腰三角形的三线合一，利用直角三角形的边角关系定理求得AD的长是解题的关键．
12．（2022•广元）如图，在正方形方格纸中，每个小正方形的边长都相等，A、B、C、D都在格点处，AB与CD相交于点P，则cs∠APC的值为（ ）
A．35B．255C．25D．55
【分析】把AB向上平移一个单位到DE，连接CE，则DE∥AB，由勾股定理逆定理可以证明△DCE为直角三角形，所以sin∠APC＝sin∠EDC即可得答案．
【解答】解：把AB向上平移一个单位到DE，连接CE，如图．
则DE∥AB，
∴∠APC＝∠EDC．
在△DCE中，有EC=22+1=5，DC=42+22=25，DE=32+42=5，
∵EC2+DC2＝DE2，
故△DCE为直角三角形，∠DCE＝90°．
∴cs∠APC＝cs∠EDC=DCDE=255．
故选：B．
【点评】本题考查了解直角三角形、平行线的性质，勾股定理，作出合适辅助线是解题关键．
13．（2022•随州）如图，已知点B，D，C在同一直线的水平地面上，在点C处测得建筑物AB的顶端A的仰角为α，在点D处测得建筑物AB的顶端A的仰角为β，若CD＝a，则建筑物AB的高度为（ ）
A．atanα−tanβB．atanβ−tanα
C．atanαtanβtanα−tanβD．atanαtanβtanβ−tanα
【分析】设AB＝x，在Rt△ABD中，tanβ=ABBD=xBD，可得BD=xtanβ，则BC＝BD+CD＝a+xtanβ，在Rt△ABC中，tanα=ABBC=xa+xtanβ，求解x即可．
【解答】解：设AB＝x，
在Rt△ABD中，tanβ=ABBD=xBD，
∴BD=xtanβ，
∴BC＝BD+CD＝a+xtanβ，
在Rt△ABC中，tanα=ABBC=xa+xtanβ，
解得x=atanαtanβtanβ−tanα．
故选：D．
【点评】本题考查解直角三角形的应用﹣仰角俯角问题，熟练掌握锐角三角函数的定义是解答本题的关键．
14．（2022•黔东南州）如图，PA、PB分别与⊙O相切于点A、B，连接PO并延长与⊙O交于点C、D，若CD＝12，PA＝8，则sin∠ADB的值为（ ）
A．45B．35C．34D．43
【分析】连接AO，BO，根据切线长定理，圆周角定理，锐角三角函数解答即可．
【解答】解连接AO，BO，
∵PA、PB分别与⊙O相切于点A、B，
∴∠PAO＝∠PBO＝90°，PA＝PB＝8，
∵DC＝12，
∴AO＝6，
∴OP＝10，
在Rt△PAO和Rt△PBO中，
PA=PBPO=PO，
∴Rt△PAO≌Rt△PBO（HL），
∴∠AOP＝∠BOP，
∴AC=BC，
∴∠ADC＝∠BDC，
∵∠AOC＝2∠ADC，
∴∠ADB＝∠AOC，
∴sin∠ADB＝sin∠AOC=APOP=45．
故选：A．
【点评】本题主要考查了切线长定理，圆周角定理，三角函数，熟练掌握相关性质是解答本题的关键．
15．（2022•泸州）如图，在平面直角坐标系xOy中，矩形OABC的顶点B的坐标为（10，4），四边形ABEF是菱形，且tan∠ABE=43．若直线l把矩形OABC和菱形ABEF组成的图形的面积分成相等的两部分，则直线l的解析式为（ ）
A．y＝3xB．y=−34x+152C．y＝﹣2x+11D．y＝﹣2x+12
【分析】分别求出矩形OABC和菱形ABEF的中心的坐标，利用待定系数法求经过两中心的直线即可得出结论．
【解答】解：连接OB，AC，它们交于点M，连接AE，BF，它们交于点N，
则直线MN为符合条件的直线l，如图，
∵四边形OABC是矩形，
∴OM＝BM．
∵B的坐标为（10，4），
∴M（5，2），AB＝10，BC＝4．
∵四边形ABEF为菱形，
BE＝AB＝10．
过点E作EG⊥AB于点G，
在Rt△BEG中，
∵tan∠ABE=43，
∴EGBG=43，
设EG＝4k，则BG＝3k，
∴BE=EG2+BG2=5k，
∴5k＝10，
∴k＝2，
∴EG＝8，BG＝6，
∴AG＝4．
∴E（4，12）．
∵B的坐标为（10，4），AB∥x轴，
∴A（0，4）．
∵点N为AE的中点，
∴N（2，8）．
设直线l的解析式为y＝ax+b，
∴5a+b=22a+b=8，
解得：a=−2b=12，
∴直线l的解析式为y＝﹣2x+12，
故选：D．
【点评】本题主要考查了矩形和菱形的性质，中点坐标的特征，直角三角形的边角关系定理，利用待定系数法确定函数的解析式是解题的关键．
16．（2022•乐山）如图，在Rt△ABC中，∠C＝90°，BC=5，点D是AC上一点，连结BD．若tan∠A=12，tan∠ABD=13，则CD的长为（ ）
A．25B．3C．5D．2
【分析】过D点作DE⊥AB于E，由锐角三角函数的定义可得5DE＝AB，再解直角三角形可求得AC的长，利用勾股定理可求解AB的长，进而求解AD的长．
【解答】解：过D点作DE⊥AB于E，
∵tan∠A=DEAE=12，tan∠ABD=DEBE=13，
∴AE＝2DE，BE＝3DE，
∴2DE+3DE＝5DE＝AB，
在Rt△ABC中，tan∠A=12，BC=5，
∴BCAC=5AC=12，
解得AC=25，
∴AB=AC2+BC2=5，
∴DE＝1，
∴AE＝2，
∴AD=AE2+DE2=12+22=5，
∴CD＝AC﹣AD=5，
故选：C．
【点评】本题主要考查解直角三角形，勾股定理，构造适当的直角三角形是解题的关键．
17．（2022•济南）数学活动小组到某广场测量标志性建筑AB的高度．如图，他们在地面上C点测得最高点A的仰角为22°，再向前70m至D点，又测得最高点A的仰角为58°，点C，D，B在同一直线上，则该建筑物AB的高度约为（ ）
（精确到1m．参考数据：sin22°≈0.37，tan22°≈0.40，sin58°≈0.85，tan58°≈1.60）
A．28mB．34mC．37mD．46m
【分析】根据题意得到AB⊥BC，然后根据三角函数的定义即可得到结论．
【解答】解：由题意可知：AB⊥BC，
在Rt△ADB中，∠B＝90°，∠ADB＝58°，
∵tan∠ADB＝tan58°=ABBD，
∴BD=ABtan58°≈AB1.60（m），
在Rt△ACB中，∠B＝90°，∠C＝22°，
∵CD＝70m，
∴BC＝CD+BD＝（70+AB1.60）m，
∴AB＝BC×tanC≈（70+AB1.60）×0.40（m），
解得：AB≈37m，
答：该建筑物AB的高度约为37m．
故选：C．
【点评】本题考查了解直角三角形的应用﹣仰角俯角问题，解题的关键是借助仰角关系结合图形利用三角函数解直角三角形．
18．（2022•宜宾）如图，在矩形纸片ABCD中，AB＝5，BC＝3，将△BCD沿BD折叠到△BED位置，DE交AB于点F，则cs∠ADF的值为（ ）
A．817B．715C．1517D．815
【分析】利用矩形和折叠的性质可得BF＝DF，设BF＝x，则DF＝x，AF＝5﹣x，在Rt△ADF中利用勾股定理列方程，即可求出x的值，进而可得cs∠ADF．
【解答】解：∵四边形ABCD是矩形，
∴∠A＝90°，AB∥CD，AD＝BC＝3，AB＝CD＝5，
∴∠BDC＝∠DBF，
由折叠的性质可得∠BDC＝∠BDF，
∴∠BDF＝∠DBF，
∴BF＝DF，
设BF＝x，则DF＝x，AF＝5﹣x，
在Rt△ADF中，32+（5﹣x）2＝x2，
∴x=175，
∴cs∠ADF=3175=1517，
故选：C．
【点评】本题主要考查矩形的性质、解直角三角形、折叠的性质、勾股定理等，解题关键是利用矩形和折叠的性质得到DF＝BF．
19．（2022•贵港）如图，某数学兴趣小组测量一棵树CD的高度，在点A处测得树顶C的仰角为45°，在点B处测得树顶C的仰角为60°，且A，B，D三点在同一直线上，若AB＝16m，则这棵树CD的高度是（ ）
A．8（3−3）mB．8（3+3）mC．6（3−3）mD．6（3+3）m
【分析】设AD＝x米，则BD＝（16﹣x）米，在Rt△ADC中，利用锐角三角函数的定义求出CD的长，然后在Rt△CDB中，利用锐角三角函数列出关于x的方程，进行计算即可解答．
【解答】解：设AD＝x米，
∵AB＝16米，
∴BD＝AB﹣AD＝（16﹣x）米，
在Rt△ADC中，∠A＝45°，
∴CD＝AD•tan45°＝x（米），
在Rt△CDB中，∠B＝60°，
∴tan60°=CDBD=x16−x=3，
∴x＝24﹣83，
经检验：x＝24﹣83是原方程的根，
∴CD＝24﹣83=8（3−3））米，
∴这棵树CD的高度是8（3−3）米，
故选：A．
【点评】本题考查了解直角三角形的应用﹣仰角俯角问题，熟练掌握锐角三角函数的定义是解题的关键．
20．（2022•荆州）如图，在平面直角坐标系中，点A，B分别在x轴负半轴和y轴正半轴上，点C在OB上，OC：BC＝1：2，连接AC，过点O作OP∥AB交AC的延长线于P．若P（1，1），则tan∠OAP的值是（ ）
A．33B．22C．13D．3
【分析】根据OP∥AB，证明出△OCP∽△BCA，得到CP：AC＝OC：BC＝1：2，过点P作PQ⊥x轴于点Q，根据∠AOC＝∠AQP＝90°，得到CO∥PQ，根据平行线分线段成比例定理得到OQ：AO＝CP：AC＝1：2，根据P（1，1），得到PQ＝OQ＝1，得到AO＝2，根据正切的定义即可得到tan∠OAP的值．
【解答】解：如图，过点P作PQ⊥x轴于点Q，
∵OP∥AB，
∴△OCP∽△BCA，
∴CP：AC＝OC：BC＝1：2，
∵∠AOC＝∠AQP＝90°，
∴CO∥PQ，
∴OQ：AO＝CP：AC＝1：2，
∵P（1，1），
∴PQ＝OQ＝1，
∴AO＝2，
∴tan∠OAP=PQAQ=12+1=13．
故选：C．
【点评】本题考查了相似三角形的判定与性质，锐角三角函数的定义，根据平行线分线段成比例定理得到OQ：AO＝CP：AC＝1：2是解题的关键．
二．填空题（共25小题）
21．（2023•泰安）在一次综合实践活动中，某学校数学兴趣小组对一电视发射塔的高度进行了测量．如图，在塔前C处，测得该塔顶端B的仰角为50°，后退60m（CD＝60m）到D处有一平台，在高2m（DE＝2m）的平台上的E处，测得B的仰角为26.6°．则该电视发射塔的高度AB为 55 m．（精确到1m．参考数据：tan50°≈1.2，tan26.6°≈0.5）
【分析】过点E作EF⊥AB，垂足为F，根据题意可得：AF＝DE＝2m，EF＝AD，BA⊥DA，然后设AC＝xm，则EF＝AD＝（x+60）m，在Rt△ABC中，利用锐角三角函数的定义求出AB的长，再在Rt△FBE中，利用锐角三角函数的定义求出BF的长，从而求出AB的长，最后列出关于x的方程，进行计算即可解答．
【解答】解：过点E作EF⊥AB，垂足为F，
由题意得：AF＝DE＝2m，EF＝AD，BA⊥DA，
设AC＝xm，
∵CD＝60m，
∴EF＝AD＝AC+CD＝（x+60）m，
在Rt△ABC中，∠BCA＝50°，
∴AB＝AC•tan50°≈1.2x（m），
在Rt△FBE中，∠BEF＝26.6°，
∴BF＝EF•tan26.6°≈0.5（x+60）m，
∴AB＝BF+AF＝[2+0.5（x+60）]m，
∴1.2x＝2+0.5（x+60），
解得：x=3207，
∴AB＝1.2x≈55（m），
∴该电视发射塔的高度AB约为55m，
故答案为：55．
【点评】本题考查了解直角三角形的应用﹣仰角俯角问题，根据题目的已知条件并结合图形添加适当的辅助线是解题的关键．
22．（2023•牡丹江）如图，将45°的∠AOB按下面的方式放置在一把刻度尺上；顶点O与尺下沿的端点重合，OA与尺下沿重合，OB与尺上沿的交点B在尺上的读数恰为2cm，若按相同的方式将22.5°的∠AOC放置在该刻度尺上，则OC与尺上沿的交点C在尺上的读数为 （22+2） cm．
【分析】由等腰直角三角形的性质得到OB=2BD＝22cm，由平行线的性质推出BC＝OB，即可求出CD长，得到OC与尺上沿的交点C在尺上的读数．
【解答】解：∵∠AOB＝45°，∠AOC＝22.5°，
∴∠BOC＝∠AOC，
∵BC∥OA，
∴∠BCO＝∠AOC，
∴∠BCO＝∠BOC，
∴BC＝OB，
∵△ODB是等腰直角三角形，
∴OB=2BD＝22cm，
∴CD＝BC+BD＝（22+2）cm．
∴OC与尺上沿的交点C在尺上的读数为（22+2）cm．
故答案为：（22+2）．
【点评】本题考查解直角三角形，等腰三角形的性质，平行线的性质，关键是由平行线的性质，推出BC＝OB，即可解决问题
23．（2023•赤峰）为发展城乡经济，建设美丽乡村，某乡对A地和B地之间的一处垃圾填埋场进行改造，把原来A地去往B地需要绕行到C地的路线，改造成可以直线通行的公路AB．如图，经勘测，AC＝6千米，∠CAB＝60°，∠CBA＝37°，则改造后公路AB的长是 9.9 千米（精确到0.1千米；参考数据：sin37°≈0.60，cs37°≈0.80，tan37°≈0.75，3≈1.73）．
【分析】过点C作CD⊥AB于点D，在Rt△ADC中利用∠CAB的余弦函数求出AD，利用∠CAB的正弦函数求出CD，然后再Rt△BCD中利用∠CBA正切函数求出DB，进而可得出答案．
【解答】解：过点C作CD⊥AB于点D，
在Rt△ADC中，AC＝6，∠CAB＝60°，cs∠CAB=ADAC，sin∠CAB=CDAC，
∴AD＝AC•cs∠CAB＝6cs60°＝3（千米），CD=ACsin∠CAB=6sin60°=33（千米），
在Rt△CDB中，∠CBA＝37°，CD=33，tan∠CBA=CDDB，
∴DB=CDtan∠CBA=33tan37°≈330.75=43（千米），
∴AB=AD+DB=3+43≈3+4×1.73≈9.9（千米）．
答：改造后公路AB的长是9.9千米．
故答案为：9.9．
【点评】此题主要考查了解直角三角形，解答此题的关键理解题意，熟练掌握锐角三角函数的定义，难点是正确的作出辅助线构造直角三角形．
24．（2023•武汉）如图，将45°的∠AOB按下面的方式放置在一把刻度尺上，顶点O与尺下沿的端点重合，OA与尺下沿重合，OB与尺上沿的交点B在尺上的读数为2cm，若按相同的方式将37°的∠AOC放置在该刻度尺上，则OC与尺上沿的交点C在尺上的读数是 2.7 cm（结果精确到0.1cm，参考数据sin37°≈0.60，cs37°≈0.80，tan37°≈0.75）
【分析】过点B作BD⊥OA于D，过点C作CE⊥OA于E，根据等腰直角三角形的性质可得CE＝2，再通过解直角三角形可求得OE的长，进而可求解．
【解答】解：过点B作BD⊥OA于D，过点C作CE⊥OA于E，
在△BOD中，∠BDO＝90°，∠DOB＝45°，
∴CE＝BD＝2cm，
在△OCE中，∠COE＝37°，∠CEO＝90°，
∴tan37°=CEOE≈0.75，
∴OE＝2.7cm，
即OC与尺上沿的交点C在尺上的读数是2.7cm．
故答案为：2.7cm．
【点评】本题主要考查解直角三角形的应用，构造直角三角形是解题的关键．
25．（2023•济宁）某数学活动小组要测量一建筑物的高度，如图，他们在建筑物前的平地上选择一点A，在点A和建筑物之间选择一点B，测得AB＝30m，用高1m（AC＝1m）的测角仪在A处测得建筑物顶部E的仰角为30°，在B处测得仰角为60°，则该建筑物的高是 （153+1）m ．
【分析】延长CD交EF与点G，根据题意可得：DB＝AC＝FG＝1m，CG⊥EF，DC＝AB＝30m，∠EDG＝60°，∠ECG＝30°，然后利用三角形的外角性质可得∠DEC＝∠ECD＝30°，从而可得ED＝CD＝30m，最后在Rt△EGD中，利用锐角三角函数的定义求出EG的长，从而利用线段的和差关系进行计算，即可解答．
【解答】解：如图：延长CD交EF于点G，
由题意得：DB＝AC＝FG＝1m，CG⊥EF，DC＝AB＝30m，∠EDG＝60°，∠ECG＝30°，
∵∠EDG是△EDC的一个外角，
∴∠DEC＝∠EDG﹣∠ECG＝30°，
∴∠DEC＝∠ECD＝30°，
∴ED＝CD＝30m，
在Rt△EGD中，EG＝ED•sin60°＝30×32=153（m），
∴EF＝EG+FG＝（153+1）m，
∴该建筑物的高是（153+1）m，
故答案为：（153+1）m．
【点评】本题考查了解直角三角形的应用﹣仰角俯角问题，根据题目的已知条件并结合图形添加适当的辅助线是解题的关键．
26．（2023•广西）如图，焊接一个钢架，包括底角为37°的等腰三角形外框和3m高的支柱，则共需钢材约 21 m（结果取整数）．（参考数据：sin37°≈0.60，cs37°≈0.80，tan37°≈0.75）
【分析】根据等腰三角形的三线合一性质可得AD＝BD=12AB，然后在Rt△ACD中，利用锐角三角函数的定义求出AC，AD的长，从而求出AB的长，最后进行计算即可解答．
【解答】解：∵CA＝CB，CD⊥AB，
∴AD＝BD=12AB，
在Rt△ACD中，∠CAD＝37°，CD＝3m，
∴AC=CDsin37°≈30.6=5（m），AD=CDtan37°≈30.75=4（m），
∴CA＝CB＝5m，AB＝2AD＝8（m），
∴共需钢材约＝AC+CB+AB+CD＝5+5+8+3＝21（m），
故答案为：21．
【点评】本题考查了解直角三角形的应用，等腰三角形的性质，熟练掌握锐角三角函数的定义，以及等腰三角形的性质是解题的关键．
27．（2023•岳阳）2023年岳阳举办以“跃马江湖”为主题的马拉松赛事．如图，某校数学兴趣小组在A处用仪器测得赛场一宣传气球顶部E处的仰角为21.8°，仪器与气球的水平距离BC为20米，且距地面高度AB为1.5米，则气球顶部离地面的高度EC是 9.5 米（结果精确到0.1米，sin21.8°≈0.3714，cs21.8°≈0.9285，tan21.8°≈0.4000）．
【分析】由题意得，四边形ABCD是矩形，根据矩形的性质得到AB＝CD＝1.5m，AD＝BC＝20m，解直角三角形即可得到结论．
【解答】解：由题意得，四边形ABCD是矩形，
∴AB＝CD＝1.5m，AD＝BC＝20m，
在Rt△ADE中，
∵AD＝BC＝20m，∠EAD＝21.8°，
∴DE＝AD•tan21.8°≈20×0.4000＝8（m），
∴CE＝CD+DE＝1.5+8＝9.5（m），
答：气球顶部离地面的高度EC是9.5m．
故答案为：9.5．
【点评】本题考查了解直角三角形的应用﹣仰角俯角问题，矩形的性质，正确地仰角的定义是解题的关键．
28．（2023•荆州）如图，无人机在空中A处测得某校旗杆顶部B的仰角为30°，底部C的俯角为60°，无人机与旗杆的水平距离AD为6m，则该校的旗杆高约为 13.8 m．（3≈1.73，结果精确到0.1）
【分析】分别利用锐角三角函数关系得出BD，DC的长，进而求出该旗杆的高度．
【解答】解：由题意可得：tan30°=BDAD=BD6=33，
解得：BD＝23（米），
tan60°=CDAD=CD6=3，
解得：DC＝63（米），
故该校的旗杆高约为：BC＝BD+DC＝83≈13.8（米），
故答案为：13.8．
【点评】此题主要考查了解直角三角形的应用﹣仰角俯角，熟练应用锐角三角函数关系是解题关键．
29．（2023•广元）如图，在平面直角坐标系中，已知点A（1，0），点B（0，﹣3），点C在x轴上，且点C在点A右方，连接AB，BC，若tan∠ABC=13，则点C的坐标为 （94，0） ．
【分析】设C（a，0），结合A，B两点的坐标利用两点间的距离可得OA＝1，AC＝a﹣1，OB＝3，BC=a2+9，通过解直角三角形可得∠OBA＝∠ABC，过C点作CD∥y轴交BA的延长线于点D，利用平行线的性质可得△OBA∽△CDA，∠ABC＝∠D，列比例式再代入计算可求解a值，进而可求解．
【解答】解：设C（a，0），
∴OC＝a，
∵点A（1，0），点B（0，﹣3），
∴OA＝1，AC＝a﹣1，OB＝3，BC=32+a2=a2+9，
在Rt△OAB中，tan∠OBA=OAOB=13，tan∠ABC=13，
∴∠OBA＝∠ABC，
过C点作CD∥y轴交BA的延长线于点D，
∴∠OBA＝∠D，∠AOB＝∠ACD，
∴△OBA∽△CDA，∠ABC＝∠D，
∴OBCD=OACA，CD＝BC，
∴OBBC=OAAC，
∴3a2+9=1a−1，
解得a＝0（舍去）或a=94，
∴C（94，0），
故答案为：（94，0）．
【点评】本题主要考查坐标与图形的性质，相似三角形的判定与性质，等腰三角形的性质，平行线的性质，两点间的距离等知识的综合运用，作适当的辅助线是解题的关键．
30．（2023•湖北）综合实践课上，航模小组用航拍无人机进行测高实践．如图，无人机从地面CD的中点A处竖直上升30米到达B处，测得博雅楼顶部E的俯角为45°，尚美楼顶部F的俯角为30°，已知博雅楼高度CE为15米，则尚美楼高度DF为 （30−53） 米．（结果保留根号）
【分析】过点E作EM⊥过点B的水平线于M，过点F作FN⊥过点B的水平线于N，先求出EM的长，在Rt△EBM中求出BM的长，然后求出BN的长，在Rt△FBN中求出FN的长，即可求出DF的长．
【解答】解：如图，过点E作EM⊥过点B的水平线于M，过点F作FN⊥过点B的水平线于N，
由题意可知CM＝DN＝AB＝30米，
又∵CE＝15米，
∴EM＝15米，
在Rt△EBM中，∠EBM＝45°，
∴BM＝EM＝15米，
又∵A是CD的中点，
∴BN＝AD＝AC＝BM＝15米，
在Rt△BFN中，tan∠FBN=FNBN，
∵∠FBN＝30°，BN＝15米，
∴FN15=33，
∴FN=53米，
∴DF＝（30−53）米．
故答案为：（30−53）．
【点评】本题主要考查解直角三角形的应用—仰角俯角问题，深入理解题意，把实际问题转化为数学问题是解决问题的关键．
31．（2023•枣庄）如图所示，桔槔是一种原始的汲水工具，它是在一根竖立的架子上加上一根细长的杠杆，末端悬挂一重物，前端悬挂水桶．当人把水桶放入水中打满水以后，由于杠杆末端的重力作用，便能轻易把水提升至所需处，若已知：杠杆AB＝6米，AO：OB＝2：1，支架OM⊥EF，OM＝3米，AB可以绕着点O自由旋转，当点A旋转到如图所示位置时∠AOM＝45°，此时点B到水平地面EF的距离为 （3+2） 米．（结果保留根号）
【分析】过点O作OC⊥BT，垂足为C，根据题意可得：BC∥OM，从而可得∠AOM＝∠OBC＝45°，再根据已知易得AO＝4米，OB＝2米，然后在Rt△OBC中，利用锐角三角函数的定义求出BC的长，从而利用线段的和差关系进行计算，即可解答．
【解答】解：过点O作OC⊥BT，垂足为C，
由题意得：BC∥OM，
∴∠AOM＝∠OBC＝45°，
∵AB＝6米，AO：OB＝2：1，
∴AO＝4米，OB＝2米，
在Rt△OBC中，BC＝OB•cs45°＝2×22=2（米），
∵OM＝3米，
∴此时点B到水平地面EF的距离＝BC+OM＝（3+2）米，
故答案为：（3+2）．
【点评】本题考查了解直角三角形的应用，根据题目的已知条件并结合图形添加适当的辅助线是解题的关键．
32．（2023•眉山）一渔船在海上A处测得灯塔C在它的北偏东60°方向，渔船向正东方向航行12海里到达点B处，测得灯塔C在它的北偏东45°方向，若渔船继续向正东方向航行，则渔船与灯塔C的最短距离是 63+6 海里．
【分析】过点C作CH⊥AB于H．证得BH＝CH，在Rt△ACH中，解直角三角形求出CH的值即可．
【解答】解：过点C作CH⊥AB于H．
∵∠DAC＝60°，∠CBE＝45°，
∴∠CAH＝90°﹣∠CAD＝30°，∠CBH＝90°﹣∠CBE＝45°，
∴∠BCH＝90°﹣45°＝45°＝∠CBH，
∴BH＝CH，
在Rt△ACH中，∠CAH＝30°，AH＝AB+BH＝12+CH，tan30°=CHAH，
∴CH=33（12+CH），
解得CH＝6（3+1）．
答：渔船与灯塔C的最短距离是6（3+1）海里．
故答案为：63+6．
【点评】本题考查的是解直角三角形的应用﹣方向角问题，正确根据题意画出辅助线，熟练掌握锐角三角函数的概念是解题的关键．
33．（2022•绥化）定义一种运算：
sin（α+β）＝sinαcsβ+csαsinβ，
sin（α﹣β）＝sinαcsβ﹣csαsinβ．
例如：当α＝45°，β＝30°时，sin（45°+30°）=22×32+22×12=6+24，则sin15°的值为 6−24 ．
【分析】把15°看成是45°与30°的差，再代入公式计算得结论．
【解答】解：sin15°＝sin（45°﹣30°）
＝sin45°cs30°﹣cs45°sin30°
=22×32−22×12
=64−24
=6−24．
故答案为：6−24．
【点评】本题考查了解直角三角形，掌握特殊角的三角函数值是解决本题的关键．
34．（2022•常州）如图，在四边形ABCD中，∠A＝∠ABC＝90°，DB平分∠ADC．若AD＝1，CD＝3，则sin∠ABD＝ 66 ．
【分析】过点D作DE⊥BC，垂足为E，如图，由已知∠A＝∠ABC＝90°，可得AD∥BC，由平行线的性质可得∠ADB＝∠CBD，根据角平分线的定义可得∠ADB＝∠CDB，则可得CD＝CB＝3，根据矩形的性质可得AD＝BE，即可得CE＝BC﹣BE，在Rt△CDE中，根据勾股定理DE=CD2−CE2，在Rt△ADB中，根据勾股定理可得BD=AD2+AB2，根据正弦三角函数的定义进行求解即可得出答案．
【解答】解：过点D作DE⊥BC，垂足为E，如图，
∵∠A＝∠ABC＝90°，
∴AD∥BC，
∴∠ADB＝∠CBD，
∵DB平分∠ADC，
∴∠ADB＝∠CDB，
∴CD＝CB＝3，
∵AD＝BE＝1，
∴CE＝BC﹣BE＝3﹣1＝2，
在Rt△CDE中，
DE=CD2−CE2=32−22=5，
∵DE＝AB，
在Rt△ADB中，
BD=AD2+AB2=12+(5)2=6，
∴sin∠ABD=ADBD=16=66．
故答案为：66．
【点评】本题主要考查了解直角三角形，根据题意作辅助线构造直角三角形应用解直角三角形的方法进行求解是解决本题的关键．
35．（2022•泰安）如图，某一时刻太阳光从窗户射入房间内，与地面的夹角∠DPC＝30°，已知窗户的高度AF＝2m，窗台的高度CF＝1m，窗外水平遮阳篷的宽AD＝0.8m，则CP的长度为 4.4m （结果精确到0.1m）．
【分析】本题涉及遮阳棚的计算问题，光线是平行光线，所以在直角三角形中，知道一个锐角的度数，一条边的长度，可以运用直角三角形边角的关系解决问题．
【解答】解：根据图形可知AD∥CP．
∵AD∥CP，∠DPC＝30°，
在Rt△ABD中，∠ADB＝30°，AD＝0.8m，
∴AB＝AD×tan∠ADB＝0.8×33≈0.46m．
∵AB＝0.46m，AF＝2m，CF＝1m，
∴BC＝2.54m，
在Rt△BCP中，∠BPC＝30°，BC＝2.54m，
∴CP=BCtan∠BPC=2.54tan30°≈4.4m．
答：CP的长度约为4.4m．
故答案为：4.4m．
【点评】考查直角三角形中边角的关系，关键是能正确的选择运用三角函数解决问题．
36．（2022•湖北）如图，有甲乙两座建筑物，从甲建筑物A点处测得乙建筑物D点的俯角α为45°，C点的俯角β为58°，BC为两座建筑物的水平距离．已知乙建筑物的高度CD为6m，则甲建筑物的高度AB为 16 m．
（sin58°≈0.85，cs58°≈0.53，tan58°≈1.60，结果保留整数）．
【分析】过点D作DE⊥AB于点E，则BE＝CD＝6m，∠ADE＝45°，∠ACB＝58°，在Rt△ADE中，∠ADE＝45°，设AE＝xm，则DE＝xm，BC＝xm，AB＝AE+BE＝（6+x）m，在Rt△ABC中，tan∠ACB＝tan58°=ABBC=6+xx≈1.60，解得x＝10，进而可得出答案．
【解答】解：过点D作DE⊥AB于点E，如图．
则BE＝CD＝6m，∠ADE＝45°，∠ACB＝58°，
在Rt△ADE中，∠ADE＝45°，
设AE＝xm，则DE＝xm，
∴BC＝xm，AB＝AE+BE＝（6+x）m，
在Rt△ABC中，
tan∠ACB＝tan58°=ABBC=6+xx≈1.60，
解得x＝10，
∴AB＝16m．
故答案为：16．
【点评】本题考查解直角三角形的应用﹣仰角俯角问题，熟练掌握锐角三角函数的定义是解答本题的关键．
37．（2022•无锡）如图，某游乐场的大型摩天轮的半径是20m，摩天轮的中心离地面距离为20.5m，摩天轮旋转1周需要18min．小明乘坐摩天轮从底部A处出发开始观光，已知B处离地面的距离为10.5m，小明第一次到达B处需要 3 min．
【分析】过B作地面所在直线的垂线BM，垂足为M，BN⊥OA于N，证明四边形BMHN是矩形，由锐角三角函数定义求出csO=ONOB=12，得∠O＝60°，再列式计算可得答案．
【解答】解：过B作地面所在直线的垂线BM，垂足为M，BN⊥OA于N，如图：
根据题意，OH＝20.5m，OA＝OB＝20m，BM＝10.5m，
∵∠BMH＝∠BNH＝∠NHM＝90°，
∴四边形BMHN是矩形，
∴BM＝NH＝10.5m，∠BNH＝90°＝∠BNO，
∴ON＝OH﹣NH＝20.5﹣10.5＝10（m），
∴csO=ONOB=1020=12，
∴∠O＝60°，
∴小明第一次到达B处需要18×60360=3（min）．
故答案为：3．
【点评】本题考查解直角三角形的应用，解题的关键是读懂题意，画出图形，求出AB所对的圆心角．
38．（2022•武汉）如图，沿AB方向架桥修路，为加快施工进度，在直线AB上湖的另一边的D处同时施工．取∠ABC＝150°，BC＝1600m，∠BCD＝105°，则C，D两点的距离是 8002 m．
【分析】过点C作CE⊥BD，在Rt△BCE中先求出CE，再在Rt△DCE中利用边角间关系求出CD．
【解答】解：过点C作CE⊥BD，垂足为E．
∵∠ABC＝150°，
∴∠DBC＝30°．
在Rt△BCE中，
∵BC＝1600m，
∴CE=12BC＝800m，∠BCE＝60°．
∵∠BCD＝105°，
∴∠ECD＝45°．
在Rt△DCE中，
∵cs∠ECD=CECD，
∴CD=CEcs45°
=80022
＝8002（m）．
故答案为：8002．
【点评】本题考查了解直角三角形的应用，掌握“直角三角形中30°角所对的边等于斜边的一半”及直角三角形的边角间关系是解决本题的关键．
39．（2022•凉山州）如图，CD是平面镜，光线从A点出发经CD上点O反射后照射到B点，若入射角为α，反射角为β（反射角等于入射角），AC⊥CD于点C，BD⊥CD于点D，且AC＝3，BD＝6，CD＝12，则tanα的值为 43 ．
【分析】先根据平行线的判定与性质可得∠A＝α，∠B＝β，从而可得∠A＝∠B，再根据相似三角形的判定证出△AOC∽△BOD，根据相似三角形的性质可得OC的长，然后根据正切的定义即可得．
【解答】解：如图，
由题意得：OE⊥CD，
又∵AC⊥CD，
∴AC∥OE，
∴∠A＝α，
同理可得：∠B＝β，
∵α＝β，
∴∠A＝∠B，
在△AOC和△BOD中∠A=∠B∠ACO=∠BDO，
∴△AOC∽△BOD，
∴OCOD=ACBD，
∴OC12−OC=36，
解得：OC＝4，
∴tanα＝tanA=OCAC=43，
故答案为：43．
【点评】本题考查了相似三角形的判定与性质、正切等知识点，掌握相似三角形的判定和性质是解题关键．
40．（2022•岳阳）喜迎二十大，“龙舟故里”赛龙舟．丹丹在汨罗江国际龙舟竞渡中心广场点P处观看200米直道竞速赛．如图所示，赛道AB为东西方向，赛道起点A位于点P的北偏西30°方向上，终点B位于点P的北偏东60°方向上，AB＝200米，则点P到赛道AB的距离约为 87 米（结果保留整数，参考数据：3≈1.732）．
【分析】过点P作PC⊥AB，垂足为P，设PC＝x米，然后分别在Rt△APC和Rt△CBP中，利用锐角三角函数的定义求出AC，BC的长，再根据AB＝200米，列出关于x的方程，进行计算即可解答．
【解答】解：过点P作PC⊥AB，垂足为C，
设PC＝x米，
在Rt△APC中，∠APC＝30°，
∴AC＝PC•tan30°=33x（米），
在Rt△CBP中，∠CPB＝60°，
∴BC＝CP•tan60°=3x（米），
∵AB＝200米，
∴AC+BC＝200，
∴33x+3x＝200，
∴x＝503≈87，
∴PC＝87米，
∴点P到赛道AB的距离约为87米，
故答案为：87．
【点评】本题考查了解直角三角形的应用﹣方向角问题，根据题目的已知条件并结合图形添加适当的辅助线是解题的关键．
41．（2022•巴中）一艘轮船位于灯塔P的南偏东60°方向，距离灯塔30海里的A处，它沿北偏东30°方向航行一段时间后，到达位于灯塔P的北偏东67°方向上的B处，此时与灯塔P的距离约为 50 海里．（参考数据：sin37°≈35，cs37°≈45，tan37°≈34）
【分析】由题意可得∠CAP＝∠EPA＝60°，∠CAB＝30°，PA＝30海里，则∠PAB＝90°，∠B＝37°，在Rt△PAB中，利用正弦函数求解即可．
【解答】解：如图所示标注字母，
根据题意得，∠CAP＝∠EPA＝60°，∠CAB＝30°，PA＝30海里，
∴∠PAB＝90°，∠APB＝180°﹣67°﹣60°＝53°，
∴∠B＝180°﹣90°﹣53°＝37°，
在Rt△PAB中，sin37°=APPB=30PB≈35，
解得PB≈50，
∴此时与灯塔P的距离约为50海里．
故答案为：50．
【点评】本题考查解直角三角形的应用﹣方向角问题，理解题意，熟练掌握锐角三角函数的定义是解题的关键．
42．（2022•连云港）如图，在6×6正方形网格中，△ABC的顶点A、B、C都在网格线上，且都是小正方形边的中点，则sinA＝ 45 ．
【分析】先构造直角三角形，然后即可求出sinA的值．
【解答】解：设每个小正方形的边长为a，
作CD⊥AB于点D，
由图可得：CD＝4a，AD＝3a，
∴AC=AD2+CD2=(3a)2+(4a)2=5a，
∴sin∠CAB=CDAC=4a5a=45，
故答案为：45．
【点评】本题考查解直角三角形，解答本题的关键是明确题意，构造出合适的直角三角形．
43．（2022•柳州）如图，某水库堤坝横断面迎水坡的坡角为α，sinα=35，堤坝高BC＝30m，则迎水坡面AB的长度为 50 m．
【分析】直接利用坡角的定义结合锐角三角函数关系得出答案．
【解答】解：∵sinα=35，堤坝高BC＝30m，
∴sinα=35=BCAB=30AB，
解得：AB＝50．
故答案为：50．
【点评】此题主要考查了解直角三角形的应用，正确掌握锐角三角函数关系是解题关键．
44．（2022•枣庄）北京冬奥会开幕式的巨型雪花状主火炬塔的设计，体现了环保低碳理念．如图所示，它的主体形状呈正六边形．若点A，F，B，D，C，E是正六边形的六个顶点，则tan∠ABE＝ 33 ．
【分析】由正六边形的性质得AB＝BC＝AC，BE垂直平分AC，再由等边三角形的性质得∠ABC＝60°，则∠ABE=12∠ABC＝30°，即可得出结论．
【解答】解：如图，连接AB、BC、AC、BE，
∵点A，F，B，D，C，E是正六边形的六个顶点，
∴AB＝BC＝AC，BE垂直平分AC，
∴△ABC是等边三角形，
∴∠ABC＝60°，
∵BE⊥AC，
∴∠ABE=12∠ABC＝30°，
∴tan∠ABE＝tan30°=33，
故答案为：33．
【点评】本题考查了正六边形的性质、等边三角形的判定与性质以及特殊角的锐角三角函数，熟练掌握正六边形的性质和等边三角形的性质是解题的关键．
45．（2022•南通）如图，B为地面上一点，测得B到树底部C的距离为10m，在B处放置1m高的测角仪BD，测得树顶A的仰角为60°，则树高AC为 （1+103） m（结果保留根号）．
【分析】在Rt△AED中，求出AE＝DE•tan60°，加上1即为AC的长．
【解答】解：如图，设DE⊥AC于点E，
在Rt△AED中，AE＝DE•tan60°＝10×3=103，
∴AC＝（1+103）（m）．
故答案为：（1+103）．
【点评】本题考查了解直角三角形的应用﹣﹣仰角俯角问题，要求学生能借助仰角构造直角三角形并解直角三角形．
三．解答题（共15小题）
46．（2023•宁夏）如图，粮库用传送带传送粮袋，大转动轮的半径为10cm，传送带与水平面成30°角．假设传送带与转动轮之间无滑动，当大转动轮转140°时，传送带上点A处的粮袋上升的高度是多少？（传送带厚度忽略不计）
【分析】设传送带上点A处的粮袋上升到点B，构建Rt△ABC，则AC∥MN，由弧长公式求出AB的长，再由含30°角的直角三角形的性质即可得出结论．
【解答】解：如图，设传送带上点A处的粮袋上升到点B，构建Rt△ABC，
则AC∥MN，
由弧长公式得：AB=140π×10180=709π（cm），
∵AC∥MN，
∴∠BAC＝∠NMA＝30°，
在Rt△ABC中，∠ACB＝90°，∠BAC＝30°，
∴BC=12AB=35π9（cm），
答：传送带上点A处的粮袋上升的高度是35π9cm．
【点评】本题考查了解直角三角形的应用—坡度坡角问题，弧长公式以及含30°角的直角三角形的性质等知识，正确作出辅助线构造直角三角形是解题的关键．
47．（2023•恩施州）小王同学学习了锐角三角函数后，通过观察广场的台阶与信号塔之间的相对位置，他认为利用台阶的可测数据与在点A，B处测出点D的仰角度数，可以求出信号塔DE的高．如图，AB的长为5m，高BC为3m．他在点A处测得点D的仰角为45°，在点B处测得点D的仰角为38.7°．A，B，C，D，E在同一平面内．
你认为小王同学能求出信号塔DE的高吗？若能，请求出信号塔DE的高；若不能，请说明理由．（参考数据：sin38.7°≈0.625，cs38.7°≈0.780，tan38.7°≈0.80，结果保留整数）
【分析】过B作BF⊥DE于F，于是得到EF＝BC＝3m，BF＝CE，根据勾股定理得到AC=AB2−BC2=4（m），根据等腰直角三角形的性质得到AE＝DE，设AE＝DE＝xm，于是得到BF＝（4+x）m，DF＝（x﹣3）m，根据三角函数的定义即可得到结论．
【解答】解：能，过B作BF⊥DE于F，
则EF＝BC＝3m，BF＝CE，
在Rt△ABC中，∵AB＝5m，BC＝3m，
∴AC=AB2−BC2=4（m），
在Rt△ADE中，∵∠DAE＝45°，
∴AE＝DE，
设AE＝DE＝xm，
∴BF＝（4+x）m，DF＝（x﹣3）m，
在Rt△BDF中，tan38.7°=DFBF=x−34+x≈0.80，
解得x＝31，
∴DE＝31m，
答：信号塔DE的高为31m．
【点评】此题主要考查解直角三角形的应用﹣仰角俯角问题，熟练掌握锐角的三角函数概念是解题关键．
48．（2023•营口）为了丰富学生的文化生活，学校利用假期组织学生到素质教育基地A和科技智能馆B参观学习，学生从学校出发，走到C处时，发现A位于C的北偏西25°方向上，B位于C的北偏西55°方向上，老师将学生分成甲乙两组，甲组前往A地，乙组前往B地，已知B在A的南偏西20°方向上，且相距1000米，请求出甲组同学比乙组同学大约多走多远的路程．（参考数据：2≈1.41，6≈2.45）
【分析】过点B作BE⊥AC，垂足为E，根据题意可得：∠ACD＝25°，∠BCD＝55°，∠FAB＝20°，AB＝1000米，CD∥FA，从而可得∠CAF＝∠ACD＝25°，进而可得∠BAC＝45°，∠ACB＝30°，然后在Rt△ABE中，利用锐角三角函数的定义求出AE和BE的长，再在Rt△BCE中，利用含30度角的直角三角形的性质求出CE和BC的长，从而求出AC的长，最后进行计算即可解答．
【解答】解：如图：过点B作BE⊥AC，垂足为E，
由题意得：∠ACD＝25°，∠BCD＝55°，∠FAB＝20°，AB＝1000米，CD∥FA，
∴∠CAF＝∠ACD＝25°，
∴∠BAC＝∠FAB+∠CAF＝45°，∠ACB＝∠BCD﹣∠ACD＝30°，
在Rt△ABE中，AE＝AB•cs45°＝1000×22=5002（米），
BE＝AB•sin45°＝1000×22=5002（米），
在Rt△BCE中，∠BCE＝30°，
∴BC＝2BE＝10002（米），CE=3BE＝5006（米），
∴AC＝AE+CE＝（5002+5006）米，
∴AC﹣BC＝5002+5006−10002=5006−5002≈520（米），
∴甲组同学比乙组同学大约多走520米的路程．
【点评】本题考查了解直角三角形的应用﹣方向角问题，根据题目的已知条件并结合图形添加适当的辅助线是解题的关键．
49．（2023•威海）如图，某育苗基地为了能够最大限度地遮挡夏季炎热的阳光和充分利用冬天的光照，计划在苗圃正上方搭建一个平行于地面的遮阳蓬．已知苗圃的（南北）宽AB＝6.5米，该地区一年中正午时刻太阳光与地平面的最大夹角是∠DAE＝76.5°，最小夹角是∠DBE＝29.5°．求遮阳蓬的宽CD和到地面的距离CB．
参考数据：sin29.5°≈49100，cs29.5°≈87100，tan29.5°≈1425，sin76.5°≈97100，cs76.5°≈23100，tan76.5°≈215．
【分析】通过作高构造直角三角形，利用直角三角形的边角关系求出DM，再由直角三角形的边角关系求出BM即可．
【解答】解：如图，过点D作DM⊥BE于点M，
设DM＝xm，则BC＝xm，
在Rt△ADM中，
∵tan76.5°=DMAM，
∴AM=DMtan76.5°，
同理BM=DMtan29.5°，
∵BM﹣AM＝AB＝6.5m，
∴DMtan29.5°−DMtan76.5°=6.5，
解得DM≈4.2（m），
即遮阳蓬到地面的高度CB约为4.2m，
∵tan76.5°=DMAM，DM＝4.2m，
∴AM=DMtan76.5°≈1（m），
∴CD＝BM＝AB+AM
＝6.5+1
＝7.5（m），
即遮阳蓬的宽CD约为7.5m．
【点评】本题考查解直角三角形的应用，掌握直角三角形的边角关系是正确解答的前提．
50．（2023•兰州）如图1是我国第一个以“龙”为主题的主题公园——“兰州龙源”、“兰州龙源”的“龙”字主题雕塑以紫铜铸造，如巨龙腾空，气势如虹，屹立在黄河北岸、某数学兴趣小组开展了测量“龙”字雕塑CD高度的实践活动，具体过程如下，如图2，“龙”字雕塑CD位于垂直地面的基座BC上，在平行于水平地面的A处测得∠BAC＝38°，∠BAD＝53°，AB＝18m．求“龙”字雕塑CD的高度，（B，C，D三点共线，BD⊥AB，结果精确到0.1m）（参考数据：sin38°≈0.62，cs38°≈0.79，tan38°≈0.78，sin53°≈0.80，cs53°≈0.60，tan53°≈1.33）
【分析】先在Rt△ABC中由AB＝18m，∠BAC＝38°得BC＝AB•tan∠BAC＝14.04（m），再在Rt△ABD中由AB＝18m，∠BAD＝53°得BD＝AB•tan∠BAD＝23.94m，然后由CD＝BD﹣BC即可得出答案．
【解答】解：在Rt△ABC中，AB＝18m，∠BAC＝38°，
∵tan∠BAC=BCAB，
∴BC＝AB•tan∠BAC＝18tan38°＝18×0.78＝14.04（m），
在Rt△ABD中，AB＝18m，∠BAD＝53°，
∵tan∠BAD=BDAB，
∴BD＝AB•tan∠BAD＝18tan53°＝18×1.33＝23.94（m），
∴CD＝BD﹣BC＝23.94﹣14.04＝9.9（m）．
答：“龙”字雕塑CD的高度约为9.9m．
【点评】此题主要考查了解直角三角形，解答此题的关键是理解题意，熟练掌握锐角三角函数的定义．
51．（2023•鄂州）鄂州市莲花山是国家4A级风景区，元明塔造型独特，是莲花山风景区的核心景点，深受全国各地旅游爱好者的青睐．今年端午节，景区将举行大型包粽子等节日庆祝活动．如图2，景区工作人员小明准备从元明塔的点G处挂一条大型竖直条幅到点E处，挂好后，小明进行实地测量，从元明塔底部F点沿水平方向步行30米到达自动扶梯底端A点，在A点用仪器测得条幅下端E的仰角为30°；接着他沿自动扶梯AD到达扶梯顶端D点，测得点A和点D的水平距离为15米，且tan∠DAB=43；然后他从D点又沿水平方向行走了45米到达C点，在C点测得条幅上端G的仰角为45°．（图上各点均在同一个平面内，且G，C，B共线，F，A，B共线，G、E、F共线，CD∥AB，GF⊥FB）．
（1）求自动扶梯AD的长度；
（2）求大型条幅GE的长度．（结果保留根号）
【分析】（1）过点D作DH⊥AB，垂足为H，然后在Rt△ADH中，利用锐角三角函数的定义求出DH的长，从而利用勾股定理求出AD的长，即可解答；
（2）过点C作CM⊥AB，垂足为M，根据题意可得：DC＝HM＝45米，DH＝CM＝20米，再利用平行线的性质可得∠DCG＝∠B＝45°，从而在Rt△CMB中，利用锐角三角函数的定义求出BM的长，进而求出BF的长，然后在Rt△AFE中，利用锐角三角函数的定义求出EF的长，再在Rt△GFB中，利用锐角三角函数的定义求出GF的长，从而利用线段的和差关系进行计算，即可解答．
【解答】解：（1）过点D作DH⊥AB，垂足为H，
在Rt△ADH中，AH＝15米，tan∠DAB=43，
∴DH＝AH•tan∠DAB＝15×43=20（米），
∴AD=AH2+DH2=152+202=25（米），
∴自动扶梯AD的长度为25米；
（2）过点C作CM⊥AB，垂足为M，
由题意得：DC＝HM＝45米，DH＝CM＝20米，
∵DC∥AB，
∴∠DCG＝∠B＝45°，
在Rt△CMB中，BM=CMtan45°=20（米），
∵AF＝30米，AH＝15米，
∴BF＝AF+AH+HM+BM＝30+15+45+20＝110（米），
在Rt△AFE中，∠EAF＝30°，
∴EF＝AF•tan30°＝30×33=103（米），
在Rt△GFB中，GF＝BF•tan45°＝110（米），
∴GE＝GF﹣EF＝（110﹣103）米，
∴大型条幅GE的长度为（110﹣103）米．
【点评】本题考查了解直角三角形的应用﹣仰角俯角问题，根据题目的已知条件并结合图形添加适当的辅助线是解题的关键．
52．（2023•长沙）2023年5月30日9点31分，“神舟十六号”载人飞船在中国酒泉卫星发射中心点火发射，成功把景海鹏、桂海潮、朱杨柱三名航天员送入到中国空间站．如图，在发射的过程中，飞船从地面O处发射，当飞船到达A点时，从位于地面C处的雷达站测得AC的距离是8km，仰角为30°；10s后飞船到达B处，此时测得仰角为45°．
（1）求点A离地面的高度AO；
（2）求飞船从A处到B处的平均速度．（结果精确到0.1km/s，参考数据：3≈1.73）
【分析】（1）根据直角三角形的性质即可得到结论；
（2）在Rt△AOC中，根据直角三角形的性质得到OC=32AC＝43（km），在Rt△BOC中，根据等腰直角三角形的性质得到OB＝OC＝43km，于是得到结论．
【解答】解：（1）在Rt△AOC中，∵∠AOC＝90°，∠ACO＝30°，AC＝8km，
∴AO=12AC=12×8=4（km），
（2）在Rt△AOC中，∵∠AOC＝90°，∠ACO＝30°，AC＝8km，
∴OC=32AC＝43（km），
在Rt△BOC中，∵∠BOC＝90°，∠BCO＝45°，
∴∠BCO＝∠OBC＝45°，
∴OB＝OC＝43km，
∴AB＝OB﹣OA＝（43−4）km，
∴飞船从A处到B处的平均速度=43−410≈0.3（km/s）．
【点评】本题考查了解直角三角形﹣仰角俯角问题，正确地求得结果是解题的关键．
53．（2023•吉林）某校数学活动小组要测量校园内一棵古树的高度，王朵同学带领小组成员进行此项实践活动，记录如下：
填写人：王朵 综合实践活动报告 时间：2023年4月20日
请结合图①、图④和相关数据写出α的度数并完成【步骤四】．
【分析】根据测角仪显示的度数和直角三角形两锐角互余即可得到α的度数，证明四边形ABDE是矩形得到DE＝AB，再解直角三角形求得CE，于是得到结论．
【解答】解：测角仪显示的度数为50°，
∴α＝90°﹣50°＝40°，
∵AB⊥BD，ED⊥BD，CE⊥AE，
∴∠ABD＝EDB＝AED＝90°，
∴四边形ABDE是矩形，
∴AE＝BD＝10m，ED＝AB＝1.54m，
在Rt△CAE中，CE＝AE•tanα＝8.39（m），
∴CD＝CE+ED＝8.39+1.54＝9.93≈9.9（m）．
答：古树高度CD约为9.9m．
【点评】本题考查了解直角三角形的应用﹣仰角俯角问题，矩形的判定和性质，熟练掌握解直角三角形的运算是解题的关键．
54．（2023•大连）如图所示是消防员攀爬云梯到小明家的场景．已知AE⊥BE，BC⊥BE，CD∥BE，AC＝10.4m，BC＝1.26m，点A关于点C的仰角为70°，则楼AE的高度为多少m？
（结果保留整数．参考数据：sin70°≈0.94，cs70°≈0.34，tan70°≈2.75）
【分析】延长CD交AE于H，于是得到CH＝BE，EH＝BC＝1.26m，解直角三角形即可得到结论．
【解答】解：延长CD交AE于H，
则CH＝BE，EH＝BC＝1.26m，
在Rt△ACH中，AC＝10.4m，∠ACH＝70°，
∴AH＝AC•sin70°＝10.4×0.94≈9.78（m），
∴AE＝AH+EH＝9.78+1.26≈11（m），
答：楼AE的高度约为11m．
【点评】本题考查了解直角三角形的应用﹣仰角俯角问题，正确地作出辅助线是解题的关键．
55．（2023•贵州）贵州旅游资源丰富．某景区为给游客提供更好的游览体验，拟在如图①景区内修建观光索道．设计示意图如图②所示，以山脚A为起点，沿途修建AB、CD两段长度相等的观光索道，最终到达山顶D处，中途设计了一段与AF平行的观光平台BC为50m．索道AB与AF的夹角为15°，CD与水平线夹角为45°，A、B两处的水平距离AE为576m，DF⊥AF，垂足为点F．（图中所有点都在同一平面内，点A、E、F在同一水平线上）
（1）求索道AB的长（结果精确到1m）；
（2）求水平距离AF的长（结果精确到1m）．
（参考数据：sin15°≈0.25，cs15°≈0.96，tan15°≈0.26，2≈1.41）
【分析】（1）通过解Rt△ABE可求得AB的长；
（2）延长BC交DF于G，证明四边形BEFG是矩形，可得EF＝BG，∠CGD＝∠BGF＝90°，再解Rt△CDG可求解CG的长，进而可求解．
【解答】解：（1）在Rt△ABE中，∠AEB＝90°，∠A＝15°，AE＝576m，
∴AB=AEcsA=576cs15°≈600（m），
即AB的长约为600m；
（2）延长BC交DF于G，
∵BC∥AE，
∴∠CBE＝90°，
∵DF⊥AF，
∴∠AFD＝90°，
∴四边形BEFG为矩形，
∴EF＝BG，∠CGD＝∠BGF＝90°，
∵CD＝AB＝600m，∠DCG＝45°，
∴CG＝CD•cs∠DCG＝600×cs45°＝600×22=3002，
∴AF＝AE+EF＝AE+BG＝AE+BC+CG＝576+50+3002≈1049（m），
即AF的长为1049m．
【点评】本题主要考查解直角三角形的应用，掌握三角函数的概念是解题的关键．
56．（2023•徐州）徐州电视塔为我市的标志性建筑之一，如图，为了测量其高度，小明在云龙公园的点C处，用测角仪测得塔顶A的仰角∠AFE＝36°，他在平地上沿正对电视塔的方向后退至点D处，测得塔顶A的仰角∠AGE＝30°．若测角仪距地面的高度FC＝GD＝1.6m，CD＝70m，求电视塔的高度AB（精确到0.1m）．（参考数据：sin36°≈0.59，cs36°≈0.81，tan36°≈0.73，sin30°＝0.50，cs30°≈0.87，tan30°≈0.58）
【分析】根据题意可得：GE⊥AB，EB＝FC＝GD＝1.6m，FG＝CD＝70m，EF＝BC，然后设EF＝BC＝xm，则GE＝（x+70）m，在Rt△AEG中，利用锐角三角函数的定义求出AE的长，再在Rt△AEF中，利用锐角三角函数的定义求出AE的长，从而列出关于x的方程，进行计算即可解答．
【解答】解：由题意得：GE⊥AB，EB＝FC＝GD＝1.6m，FG＝CD＝70m，EF＝BC，
设EF＝BC＝xm，
∴GE＝EF+FG＝（x+70）m，
在Rt△AEG中，∠AGE＝30°，
∴AE＝EG•tan30°≈0.58（x+70）m，
在Rt△AEF中，∠AFE＝36°，
∴AE＝EF•tan36°≈0.73x（m），
∴0.73x＝0.58（x+70），
解得：x≈270.67，
∴AE＝0.73x≈197.59（m），
∴AB＝AE+BE＝197.59+1.6≈199.2（m），
∴电视塔的高度AB约为199.2m．
【点评】本题考查了解直角三角形的应用﹣仰角俯角问题，熟练掌握锐角三角函数的定义是解题的关键．
57．（2023•湘潭）问题情境：筒车是我国古代发明的一种水利灌溉工具，既经济又环保．明朝科学家徐光启在《农政全书》中用图画描绘了筒车的工作原理（如图①）．假定在水流量稳定的情况下，筒车上的每一个盛水筒都按逆时针做匀速圆周运动，每旋转一周用时120秒．
问题设置：把筒车抽象为一个半径为r的⊙O．如图②，OM始终垂直于水平面，设筒车半径为2米．当t＝0时，某盛水筒恰好位于水面A处，此时∠AOM＝30°，经过95秒后该盛水筒运动到点B处．
问题解决：
（1）求该盛水筒从A处逆时针旋转到B处时，∠BOM的度数；
（2）求该盛水筒旋转至B处时，它到水面的距离．（结果精确到0.1米）（参考数据2≈1.414，3≈1.732）
【分析】（1）求出筒车每秒转过的度数，再根据周角的定义进行计算即可；
（2）根据直角三角形的边角关系分别求出OD、OC即可．
【解答】解：（1）由于筒车每旋转一周用时120秒．所以每秒转过360°÷120＝3°，
∴∠BOM＝360°﹣3°×95﹣30°＝45°；
（2）如图，过点B、点A分别作OM的垂线，垂足分别为点C、D，
在Rt△AOD中，∠AOD＝30°，OA＝2米，
∴OD=32OA=3（米）．
在Rt△BOC中，∠BOC＝45°，OB＝2米，
∴OC=22OB=2（米），
∴CD＝OD﹣OC=3−2≈0.3（米），
即该盛水筒旋转至B处时到水面的距离约为0.3米．
【点评】本题考查解直角三角形的应用，掌握直角三角形的边角关系是正确解答的前提．
58．（2023•常德）今年“五一”长假期间，小陈、小余同学和家长去沙滩公园游玩，坐在如图的椅子上休息时，小陈感觉很舒服，激发了她对这把椅子的好奇心，就想出个问题考考同学小余，小陈同学先测量，根据测量结果画出了图1的示意图（图2）．在图2中，已知四边形ABCD是平行四边形，座板CD与地面MN平行，△EBC是等腰三角形且BC＝CE，∠FBA＝114.2°，靠背FC＝57cm，支架AN＝43cm，扶手的一部分BE＝16.4cm．这时她问小余同学，你能算出靠背顶端F点距地面（MN）的高度是多少吗？请你帮小余同学算出结果（最后结果保留一位小数）．（参考数据：sin65.8°＝0.91，cs65.8°＝0.41，tan65.8°＝2.23）
【分析】过点F作FQ⊥CD于点Q，过C作CH⊥AB于点H，求出FQ、BH的值解答即可
【解答】解：过点F作FQ⊥CD于点Q，
∵四边形ABCD是平行四边形，∠FBA＝114.2°，
∴∠FCQ＝180°﹣114.2°＝65.8°，FQ＝FC•sin∠FCQ＝57sin65.8°，
过点A作AP⊥MN于点P，
由题意知AB∥CD∥MN，FC∥AN，
则∠ANP＝∠FCQ＝65.8°，又AN＝43cm，
∴AP＝AN•sin∠ANP＝43sin65.8°，
过C作CH⊥AB于点H，
∵BC＝CE，EB＝16.4，
∴BH＝8.2，
∴CH＝BH•tan∠CBH＝8.2×2.23≈18.29，
∴靠背顶端F点距地面（MN）高度为
FQ+AP﹣HC＝57sin65.8°+43sin65.8°﹣18.29＝100×0.91﹣18.29＝72.71≈72.7cm．
【点评】本题考查了解直角三角形，掌握平行四边形是解题的关键．
59．（2023•辽宁）暑假期间，小明与小亮相约到某旅游风景区登山．需要登顶600m高的山峰，由山底A处先步行300m到达B处，再由B处乘坐登山缆车到达山顶D处．已知点A，B，D，E，F在同一平面内，山坡AB的坡角为30°，缆车行驶路线BD与水平面的夹角为53°（换乘登山缆车的时间忽略不计）．
（1）求登山缆车上升的高度DE；
（2）若步行速度为30m/min，登山缆车的速度为60m/min，求从山底A处到达山顶D处大约需要多少分钟（结果精确到0.1min）．
（参考数据：sin53°≈0.80，cs53°≈0.60，tan53°≈1.33）
【分析】（1）根据直角三角形的边角关系求出BM，进而求出DE即可；
（2）利用直角三角形的边角关系，求出BD的长，再根据速度、路程、时间的关系进行计算即可．
【解答】解：（1）如图，过点B作BM⊥AF于点M，由题意可知，∠A＝30°，∠DBE＝53°，DF＝600m，AB＝300m，
在Rt△ABM中，∠A＝30°，AB＝300m，
∴BM=12AB＝150m＝EF，
∴DE＝DF﹣EF＝600﹣150＝450（m），
答：登山缆车上升的高度DE为450m；
（2）在Rt△BDE中，∠DBE＝53°，DE＝450m，
∴BD=DEsin∠DBE
≈4500.80
＝562.5（m），
∴需要的时间t＝t步行+t缆车
=30030+562.560
≈19.4（min），
答：从山底A处到达山顶D处大约需要19.4分钟．
【点评】本题考查解直角三角形的应用，掌握直角三角形的边角关系是正确解答的前提．
60．（2023•通辽）如图，一艘海轮位于灯塔P的北偏东72°方向，距离灯塔100nmile的A处，它沿正南方向航行一段时间后，到达位于灯塔P的南偏东40°方向上的B处．这时，B处距离灯塔P有多远（结果取整数）？（参考数据：sin72°≈0.95，cs72°≈0.31，tan72°≈3.08，sin40°≈0.64，cs40°≈0.77，tan40°≈0.84）
​
【分析】根据题意可得：PC⊥AB，EF∥AB，从而可得∠A＝∠EPA＝72°，∠B＝∠BPF＝40°，然后在Rt△APC中，利用锐角三角函数的定义求出PC的长，再在Rt△BPC中，利用锐角三角函数的定义求出BP的长，即可解答．
【解答】解：如图：
由题意得：PC⊥AB，EF∥AB，
∴∠A＝∠EPA＝72°，∠B＝∠BPF＝40°，
在Rt△APC中，AP＝100海里，
∴PC＝AP•sin72°≈100×0.95＝95（海里），
在Rt△BCP中，BP=PCsin40°≈950.64≈148（海里），
∴B处距离灯塔P约有148海里．
【点评】本题考查了解直角三角形的应用﹣方向角问题，熟练掌锐角三角函数的定义是解题的关键．
活动任务：测量古树高度
活动过程
【步骤一】设计测量方案
小组成员讨论后，画出如图①的测量草图，确定需测的几何量．
【步骤二】准备测量工具
自制测角仪，把一根细线固定在半圆形量角器的圆心处，细线的另一端系一个小重物，制成一个简单的测角仪，利用它可以测量仰角或俯角，如图②所示．准备皮尺．
【步骤三】实地测量并记录数据
如图③，王朵同学站在离古树一定距离的地方，将这个仪器用手托起，拿到眼前，使视线沿着仪器的直径刚好到达古树的最高点．如图④，利用测角仪，测量后计算得出仰角α．测出眼睛到地面的距离AB．测出所站地方到古树底部的距离BD．
α＝ 40° ．
AB＝1.54m．
BD＝10m.
【步骤四】计算古树高度CD．（结果精确到0.1m）
（参考数据：sin40°≈0.643，cs40°≈0.766，tan40°≈0.839）