八年级上册数学第一次月考试题及答案(8套)

这是一份八年级上册数学第一次月考试题及答案(8套)，共33页。试卷主要包含了选择题，填空题，解答题，解答题．等内容，欢迎下载使用。

1．下列每组数分别表示三根木棒的长，将它们首尾连接后，能摆成三角形的一组是（ ）
A．1，2，1 B．1，2，3 C．1，2，2 D．1，2，4
2．下列图形中不具有稳定性的是（ ）
A．锐角三角形B．长方形C．直角三角形D．等腰三角形
3．如图，∠1=120°，∠E=80°，则∠A的大小是（ ）
A．10°B．40°C．30°D．80°
4．一个多边形的每个外角都等于72°，则这个多边形的内角和为（ ）
A．180°B．720°C．540°D．360°
5．过多边形的一个顶点可以引出6条对角线，则多边形的边数是（ ）
A．7B．8C．9D．10
6．如图所示，亮亮书上的三角形被墨迹污染了一部分，很快他就根据所学知识画出一个与书上完全一样的三角形，那么这两个三角形完全一样的依据是（ ）
A．SSSB．SASC．AASD．ASA

7．如图所示，若△ABE≌△ACF，且AB=6，AE=2，则BF的长为（ ）
A．2B．3C．5D．4
8．下列条件中，不能判定△ABC≌△A′B′C′，的是（ ）
A．∠A=∠A，∠C=∠C，AC=A′C′ B．∠B=∠B′，BC=B′C′，AB=A′B′
C．∠A=∠A′=80°，∠B=60°，∠C′=40°，AB=A′B′D．∠A=∠A′，BC=B′C′，AB=A′B′
9．下列说法中，正确的是（ ）
A．两边及其中一边的对角分别相等的两个三角形全等
B．两边及其中一边上的高分别相等的两个三角形全等
C．斜边和一锐角分别相等的两个直角三角形全等
D．面积相等的两个三角形全等
10．把一块直尺与一块三角板如图放置，若∠2=130°，则∠1的度数为（ ）
A．30°B．35°C．40°D．45°

二、填空题（共8小题，每小题3分，共24分）
11．在△ABC中，已知∠A=30°，∠B=70°，则∠C的度数是 度．
12．如图，在△ABC中，D、E分别是BC、AD的中点，△ABC的面积为6cm2，则△BDE的面积为 ．
13．如图，一个直角三角形纸片，剪去直角后，得到一个四边形，则∠1+∠2= 度．
14．一个多边形的每个外角都是60°，则这个多边形边数为 ．
15．已知一个等腰三角形的两边长分别为2cm、3cm，那么它的第三边长为 ．
16．如图，已知AB=BD那么添加一个条件 后，可判定△ABC≌△ADC．
17．已知△ABC≌△DEF，∠A=40°，∠C=60°，则∠E= ．
18．一个三角形的三条边的长分别是3，5，7，另一个三角形的三条边的长分别是3，3x﹣2y，x+2y，若这两个三角形全等，则x+y的值是 ．
三.解答题（共46分）
19．（6分）如图，在△ABC中，∠ADB=∠ABD，∠DAC=∠DCA，∠BAD=32°，求∠BAC的度数．
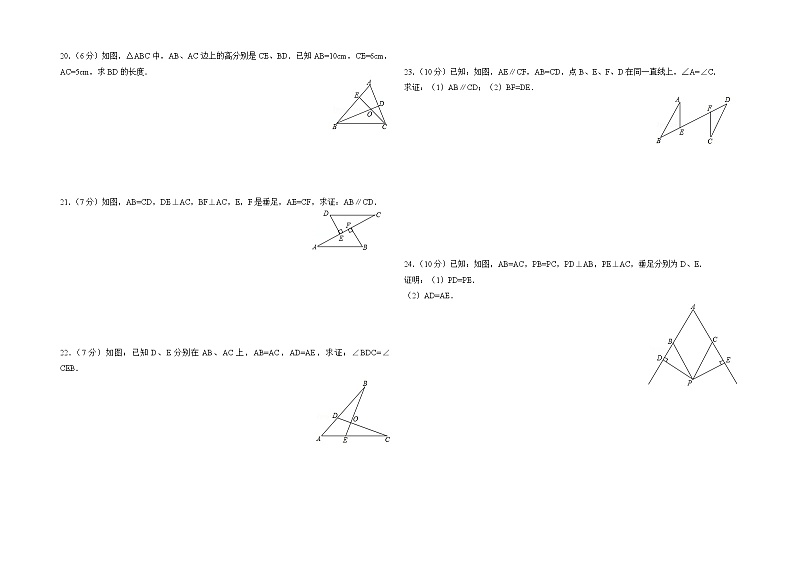
20．（6分）如图，△ABC中，AB、AC边上的高分别是CE、BD．已知AB=10cm，CE=6cm，AC=5cm，求BD的长度．
21．（7分）如图，AB=CD，DE⊥AC，BF⊥AC，E，F是垂足，AE=CF，求证：AB∥CD．
22．（7分）如图：已知D、E分别在AB、AC上，AB=AC，AD=AE，求证：∠BDC=∠CEB．
23．（10分）已知：如图，AE∥CF，AB=CD，点B、E、F、D在同一直线上，∠A=∠C．
求证：（1）AB∥CD；（2）BF=DE．
24．（10分）已知：如图，AB=AC，PB=PC，PD⊥AB，PE⊥AC，垂足分别为D、E．
证明：（1）PD=PE．
（2）AD=AE．

八年级（上）第一次月考数学试卷一 参考答案
一、选择题
1． C． 2． B． 3． B． 4． C． 5． C． 6． D． 7． D． 8． D． 9． C． 10． C．
二、填空题11． 80°． 12．． 13． 270°．14． 6． 15． 2cm或3cm． 16． BC=CD． 17． 80°．
18． 5或4
三.解答题（共46分）
19.解：在三角形ABD中，∠ADB=∠ABD=（180°﹣32°）=74°，
在三角形ADC中，∠DAC=∠DCA=∠ADB=37°，
∴∠BAC=∠DAC+∠BAD=37°+32°=69°．
20．解：∵△ABC中，AB、AC边上的高分别是CE、BD．AB=10cm，CE=6cm，AC=5cm，
∴△ABC的面积=，
即cm．
21．证明：如图，∵AE=CF，
∴AE+EF=CF+EF，即AF=EC．
又∵BF⊥AC，DE⊥AC，∴∠AFB=∠CED=90°．
在Rt△ABF与Rt△CDE中，
，
∴Rt△ABF≌Rt△CDE（HL），
∴∠C=∠A，∴AB∥CD．
22．证明：在△ABE和△ACD中，
，
∴△ABE≌△ACD，∴∠B=∠C，
∵∠BDC=∠A+∠C，∠CEB=∠A+∠B，
∴∠BDC=∠CEB．
23．解：（1）∵AB∥CD，∴∠B=∠D．
在△ABE和△CDF中，
，
∴△ABE≌△CDF（ASA），∴∠B=∠D，∴AB∥CD；
（2）∵△ABE≌△CDF，
∴BE=DF．∴BE+EF=DF+EF，∴BF=DE．
24．证明：（1）连接AP．
在△ABP和△ACP中，
，
∴△ABP≌△ACP（SSS）．∴∠BAP=∠CAP，
又∵PD⊥AB，PE⊥AC，垂足分别为D、E，
∴PD=PE（角平分线上点到角的两边距离相等）．
（2）在△APD和△APE中，
∵，
∴△APD≌△APE（AAS），
∴AD=AE；

八年级数学上第一次月考试题（二）
一、选择题(每小题3分，共30分)
1．在△ABC中，∠A，∠B都是锐角，则∠C是（ ）
A．锐角B．直角C．钝角D．以上都有可能
2．下列各组线段，不能组成三角形的是（ ）
A．1，2，3B．2，3，4C．3，4，5D．5，12，13
3．若一个多边形的内角和与它的外角和相等，则这个多边形是（ ）
A．三角形B．四边形C．五边形D．六边形
4．已知，在△ABC中，∠A=60°，∠C=80°，则∠B=（ ）
A．60°B．30°C．20°D．40°
5．下面四个图形中，能判断∠1＞∠2的是（ ）
A．B．C．D．
6．已知，如图，AB∥CD，∠A=70°，则∠ACD=（ ）
A．55°B．70°C．40°D．110°
7．如图，已知△ABC中，∠C=90°，若沿图中虚线剪去∠C，则∠1+∠2等于（ ）
A．90°B．135°C．270°D．315°

8．如图，E，B，F，C四点在一条直线上，EB=CF，∠A=∠D，再添一个条件仍不能证明△ABC≌△DEF的是（ ）
A．AB=DEB．DF∥ACC．∠E=∠ABCD．AB∥DE
9．如图，点O是△ABC内一点，∠A=80°，∠1=15°，∠2=40°，则∠BOC等于（ ）
A．95°B．120°C．135°D．无法确定
10．正多边形的一个内角等于144°，则该多边形是正（ ）边形．
A．8B．9C．10D．11
二、填空题(每小题3分，共24分)
11．三角形的两边长分别是10和8，则第三边的取值范围是 ．
12．杜师傅在做完门框后，为防止门框变形常常需钉两根斜拉的木条，这样做的数学原理是 ．
13．如图，三角形纸片ABC，AB=10cm，BC=7cm，AC=6cm，沿过点B的直线折叠这个三角形，使顶点C落在AB边上的点E处，折痕为BD，则△AED的周长为 cm．

14．如图，在Rt△ABC中，∠C=90°，∠A=30°，BD是∠ABC的平分线，则∠ADB= 度．
15．如图，若∠A=70°，∠ABD=120°，则∠ACE= ．
16．已知△ABC≌△DEF，∠A=52°，∠B=57°，则∠F= ．
17．如图，△ABD≌△ACE，AD=8cm，AB=3cm，则BE= cm．
18．已知△ABC≌△DEF，且∠A=90°，AB=6，AC=8，BC=10，△DEF中最大边长是 ，最大角是 度．
三、解答题
19．（8分）按要求画图，并描述所作线段．
（1）过点A画三角形的高线；
（2）过点B画三角形的中线；
（3）过点C画三角形的角平分线；
（4）作∠D=∠C（尺规作图，不写作法保留作图痕迹）．
20．（10分）如图，已知D为△ABC边BC延长线上一点，DF⊥AB于F交AC于E，∠A=35°，∠D=42°，求∠ACD的度数．
21．（8分）一个多边形的内角和是外角和的3倍，求这个多边形的边数．
22．（8分）如图所示，已知△ABC≌△FED，且BC=ED，FD=5cm，AD=2cm，那么AB与EF平行吗？为什么？
23．（10分）如图：AE=DE，BE=CE，AC和BD相交于点E，求证：AB=DC．
24．（10分）如图，AB=AC，AD=AE，∠1=∠2，求证：△ABD≌△ACE．
25．（12分）如图，点B、E、C、F在同一直线上，BE=CF，AB=DE，AC=DF．
求证：AB∥DE．


八年级（上）第一次月考数学试卷二 参考答案
一、选择题1． D． 2． A． 3B． 4． D． 5． D． 6． B． 7． C． 8． A． 9． C． 10C．
二、11． 2＜x＜18 12．三角形的稳定性． 13． 9cm． 14．120． 15．130°． 16． 71°．17． 5．
18． 90°；10．
三、19．解：（1）如图所示：AH即为所求；
（2）如图所示：BE即为所求；（3）如图所示：CF即为所求；（4）如图所示，∠D即为所求．
20．解：∵∠AFE=90°，
∴∠AEF=90°﹣∠A=90°﹣35°=55°，
∴∠CED=∠AEF=55°，
∴∠ACD=180°﹣∠CED﹣∠D=180°﹣55°﹣42°=83°．
答：∠ACD的度数为83°．
21．解：设这个多边形是n边形，由题意得：
（n﹣2）×180°=360°×3，
解得：n=8．
答：这个多边形的边数是8．
22．解：AB与EF平行．
理由：∵△ABC≌△FED，
∴∠F=∠A，
∴AB∥EF．
23．证明：∵在△ABE与△DCE中，
，
∴△ABE≌△DCE（SAS），
∴AB=CD．
24．证明：∵∠1=∠2，
∴∠CAE=∠BAD，
∵AB=AC，AD=AE，
∴△ABD≌△ACE．
25．证明：∵BE=CF，
∴BC=EF，
在△ABC和△DEF中，
，
∴△ABC≌△DEF（SSS），
∴∠B=∠DEF，
∴AB∥DE．

八年级数学上第一次月考试题（三）
一、选择题（每小题3分，共30分）
1．下列所给的各组线段，能组成三角形的是（ ）
A．10cm、20cm、30cm B．20cm、30cm、40cm
C．10cm、20cm、40cm D．10cm、40cm、50cm
2．某同学把一块三角形的玻璃打碎成了3块，现在要到玻璃店去配一块完全一样的玻璃，那么最省事方法是（ ）
A．带①去B．带②去C．带③去D．①②③都带去
3．如果从一个多边形的一个顶点出发作它的对角线，最多能将多边形分成2011个三角形，那么这个多边形是（ ）
A．2012边形B．2013边形C．2014边形D．2015边形
4．正多边形的一个内角等于144°，则该多边形是正（ ）边形．
A．8B．9C．10D．11
5．等腰三角形中，一个角为50°，则这个等腰三角形的顶角的度数为（ ）
A．150°B．80°C．50°或80°D．70°
6．下列说法正确的是（ ）
A．全等三角形是指形状相同大小相等的三角形 B．全等三角形是指面积相等的三角形
C．周长相等的三角形是全等三角形 D．所有的等边三角形都是全等三角形

7．如图所示，在下列条件中，不能判断△ABD≌△BAC的条件是（ ）
A．∠D=∠C，∠BAD=∠ABC B．∠BAD=∠ABC，∠ABD=∠BAC
C．BD=AC，∠BAD=∠ABC D．AD=BC，BD=AC
8．如图，E，B，F，C四点在一条直线上，EB=CF，∠A=∠D，再添一个条件仍不能证明△ABC≌△DEF的是（ ）
A．AB=DE B．DF∥AC C．∠E=∠ABC D．AB∥DE
9．△ABC中，AC=5，中线AD=7，则AB边的取值范围是（ ）
A．1＜AB＜29 B．4＜AB＜24 C．5＜AB＜19 D．9＜AB＜19
10．如图，点B、C、E在同一条直线上，△ABC与△CDE都是等边三角形，则下列结论不一定成立的是（ ）
A．△ACE≌△BCDB．△BGC≌△AFCC．△DCG≌△ECFD．△ADB≌△CEA

二、填空题（每小题4分，共16分）
11．如图，△ABC≌△DEF，A与D，B与E分别是对应顶点，∠B=32°，∠A=68°，AB=13cm，则∠F= 度，DE= cm．
12．如图，∠1= ．

13．如图，AE=BF，AD∥BC，AD=BC，则有△ADF≌ ，且DF= ．
14．如图，已知∠1=∠2，要说明△ABC≌△BAD．
（1）若以“SAS”为依据，则需添加一个条件是 ；
（2）若以“AAS”为依据，则需添加一个条件是 ；
（3）若以“ASA”为依据，则需添加一个条件是 ．
三、解答题（共54分）
15．（9分）尺规作图：已知∠α，求作：∠A使∠A=∠α（ 不写作法，保留痕迹 ）
16．（9分）如图，已知D为△ABC边BC延长线上一点，DF⊥AB于F交AC于E，∠A=35°，∠D=42°，求∠ACD的度数．
17．（9分）如图所示，点B、F、C、E在同一条直线上，AB∥DF，AC∥DE，AC=DE，FC与BE相等吗？请说明理由．
18．（9分）如图，AC=DF，AD=BE，BC=EF．求证（1）△ABC≌△DEF； （2）AC∥DF．
19．（9分）如图，AB=AC，AD=AE，∠1=∠2，求证：△ABD≌△ACE．
20．（9分）如图，已知点B、D、E、C四点在一条直线上，且△ABE≌△ACD．
求证（1）BD=CE；
（2）△ABD≌△ACE．

八年级（上）第一次月考数学试卷三参考答案
一、1． B．2． C． 3． B． 4． C． 5． C． 6． A． 7． C． 8． A． 9． D． 10． D．
二、11． 13cm． 12． 120°． 13．△BCE，CE． 14．（1）BC=AD；（2）∠C=∠D；（3）∠BAC=∠ABD．
三、解答题（共54分）
15．解：如图∠A即为所求．

16．解：∵∠AFE=90°，
∴∠AEF=90°﹣∠A=90°﹣35°=55°，
∴∠CED=∠AEF=55°，
∴∠ACD=180°﹣∠CED﹣∠D=180°﹣55°﹣42°=83°．
答：∠ACD的度数为83°．
17．解：相等；理由如下：
∵AB∥DF，AC∥DE，
∴∠B=∠F，∠ACB=∠FED，
在△ABC和△DEF中
，
∴△ABC≌△DEF，
∴BC=EF，
∴BC﹣EC=EF﹣EC，
即BE=CF．
18证明：（1）∵AD=BE，
∴AD+DB=BE+DB，
∴AB=DE，
在△ABC和△DEF中
∴△ABC≌△DEF（SSS）；
（2）∵△ABC≌△DEF，
∴∠A=∠EDF，
∴AC∥DF．
19．证明：∵∠1=∠2，
∴∠CAE=∠BAD，
∵AB=AC，AD=AE，
∴△ABD≌△ACE．
20．证明：（1）∵△ABE≌△ACD，
∴EB=DC，
∴EB﹣DE=DC﹣DE，
即DB=EC；
（2）∵△ABE≌△ACD，
∴∠B=∠C，AB=AC，
在△ABD和△ACE中，
，
∴△ABD≌△ACE（SAS）．

八年级数学上第一次月考试题（四）
一、选择题（每小题3分，共36分）
1．下列几组线段能组成三角形的是（ ）
A．3cm、5cm、8cm B．2cm、2cm、6cm C．1.2cm、1.2cm、1.2cm D．8cm、6cm、15cm
2．如图，∠ACB＞90°，AD⊥BC，BE⊥AC，CF⊥AB，垂足分别为点D、点E、点F，△ABC中AC边上的高是（ ）
A．CF B．BE C．AD D．CD
3．多边形的每个内角都等于150°，则从此多边形的一个顶点出发可作的对角线共有（ ）
A．8条 B．9条 C．10条 D．11条
4．在△ABC中，∠A=105°，∠B﹣∠C=15°，则∠C的度数为（ ）
A．35° B．60° C．45° D． 30°
5．如图，已知∠1=∠2，AC=AD，增加下列条件：①AB=AE；②BC=ED；③∠C=∠D；④∠B=∠E．其中能使△ABC≌△AED成立的条件有（ ）

A．4个B．3个C．2个D．1个
6．如图，在△ACB中，∠ACB=100°，∠A=20°，D是AB上一点．将△ABC沿CD折叠，使B点落在AC边上的B′处，则∠ADB′等于（ ）
A．25°B．30°C．35°D．40°
7．小明同学在用计算器计算某n边形的内角和时，不小心多输入一个内角，得到和为2016°，则n等于（ ）
A．11B．12C．13D．14
8．如图是由4个相同的小正方形组成的网格图，其中∠1+∠2等于（ ）
A．150°B．180°C．210°D．225°
9．在等腰△ABC中，AB=AC，中线BD将这个三角形的周长分为15和12两个部分，则这个等腰三角形的底边长为（ ）
A．7B．11C．7或11D．7或10
10．等腰三角形一腰上的高与另一腰的夹角为45°，则其顶角为（ ）
A．45°B．135°C．45°或67.5°D．45°或135°
11．如图，五边形ABCDE中，AB∥CD，∠1、∠2、∠3分别是∠BAE、∠AED、∠EDC的外角，则∠1+∠2+∠3等于（ ）

A．90°B．180°C．210°D．270°
12．如图，△ABC的角平分线CD、BE相交于F，∠A=90°，EG∥BC，且CG⊥EG于G，下列结论：①∠CEG=2∠DCB；②CA平分∠BCG；③∠ADC=∠GCD；④∠CGE=2∠DFB，其中正确的结论有（ ）个．
A．1B．2C．3D．4
二、填空题（每小题4分，共24分）
13．如图，点O在△ABC内，且到三边的距离相等，若∠A=60°，则∠BOC= ．

14．如图所示，在△ABC中，∠B=∠C=50°，BD=CF，BE=CD，则∠EDF的度数是 ．
15．如图，BD是∠ABC的角平分线，DE⊥AB于E，△ABC的面积是30cm2，AB=18cm，BC=12cm，则DE= cm．
16．在平面直角坐标系中，点A（2，0），B（0，4），作△BOC，使△BOC与△ABO全等，则点C坐标为 ．（点C不与点A重合）
17．如图，已知P（3，3），点B、A分别在x轴正半轴和y轴正半轴上，∠APB=90°，则OA+OB= ．
18．如图，AE⊥AB，且AE=AB，BC⊥CD，且BC=CD，请按照图中所标注的数据，计算图中实线所围成的图形的面积S是 ．

三、解答题（满分60分）
19．（10分）已知：BE⊥CD，BE=DE，BC=DA，求证：①△BEC≌△DEA；②DF⊥BC．
20．（8分）如图，四边形ABCD中，E点在AD上，∠BAE=∠BCE=90°，且BC=CE，AB=DE．求证：△ABC≌△DEC．
21．（10分）如图，已知△ABC为等边三角形（三条边相等三个角为60°的三角形），点D、E分别在BC、AC边上，且AE=CD，AD与BE相交于点F．
（1）求证：△ABE≌△CAD；（2）求∠BFD的度数．
22．（10分）如图，在△ABC中，∠B=∠C，点D在BC边上，点E在AC边上，且∠ADE=∠AED，连接DE．（1）若∠BAD=60°，求∠CDE的度数；（2）猜想∠CDE与∠BAD的数量关系，并说明理由．
23．（10分）如图，E、F分别是正方形ABCD的边BC、CD上一点，且BE+DF=EF，求∠EAF的度数．
24．（12分）已知点P为∠EAF平分线上一点，PB⊥AE于B，PC⊥AF于C，点M、N分别是射线AE、AF上的点．（1）如图1，当点M在线段AB上，点N在线段AC的延长线上，且PM=PN，求证：BM=CN；（2）在（1）的条件下，直接写出线段AM，CN与AC之间的数量关系 ；
（3）如图2，当点M在线段AB的延长线上，点N在线段AC上时，且∠MAN+∠MPN=180°，若AC：PC=2：1，PC=4，求四边形ANPM的面积．

八年级（上）第一次月考数学试卷四参考答案
一、1． C． 2． B． 3． B． 4． D． 5． B． 6． D． 7． D． 8． B．9． C．10． D．11． B．
12． C．
二、13． 120°．14． 50°． 15． 2．16．（2，4）或（﹣2，0）或（﹣2，4）． 17． 6．
18． 50．
三、解答题（满分60分）
19．证明：（1）∵BE⊥CD，
∴∠BEC=∠DEA=90°，
又∵BE=DE，BC=DA，
∴△BEC≌△DEA（HL）；
（2）∵△BEC≌△DEA，
∴∠B=∠D．
∵∠D+∠DAE=90°，∠DAE=∠BAF，
∴∠BAF+∠B=90°．
即DF⊥BC．
20．证明：∵∠BAE=∠BCE=90°，
∴∠ABE+∠AEC=180°，
∵∠AEC+∠DEC=180°，
∴∠DEC=∠B，
在△ABC和△DEC中
，
∴△ABC≌△DEC（SAS）．
21．证明：（1）∵△ABC为等边三角形，
∴AB=BC=AC，∠ABC=∠ACB=∠BAC=60°．
在△ABE和△CAD中，
，
∴△ABE≌△CAD（SAS），
（2）∵△ABE≌△CAD，
∴∠ABE=∠CAD．[来源:学+科+网]
∵∠BAD+∠CAD=60°，
∴∠BAD+∠EBA=60°．
∵∠BFD=∠ABE+∠BAD，
∴∠BFD=60°．

22．解：（1）∵∠BAD=60°，∠B=∠C，
∴∠ADC=∠BAD+∠B=60°+∠B，∠DAE=∠BAC﹣∠BAD=180°﹣2∠B﹣60°=120°﹣2∠B，
∴∠ADE=∠AED=（180°﹣120°+2∠B）=30°+∠B，
∴∠CDE=∠ADC﹣∠ADE=（60°+∠B）﹣（30°+∠B）=30°；
（2）∠BAD=2∠CDE，理由：
设∠BAD=x，
∴∠ADC=∠BAD+∠B=∠B+x，
∠DAE=∠BAC﹣∠BAD=180°﹣2∠C﹣x，
∴∠ADE=∠AED=∠C+x，
∴∠CDE=∠B+x﹣（∠C+x）=x，
∴∠BAD=2∠CDE．
23．解：延长EB使得BG=DF，连接AG，
在△ABG和△ADF中，
，
可得△ABG≌△ADF（SAS），
∴∠DAF=∠BAG，AF=AG，
又∵EF=DF+BE=EB+BG=EG，AE=AE，
在△AEG和△AEF中，
，
∴△AEG≌△AEF（SSS），
∴∠EAG=∠EAF，
∵∠DAF+∠EAF+∠BAE=90°
∴∠EAG+∠EAF=90°，
∴∠EAF=45°．
24．（1）证明：∵点P为∠EAF平分线上一点，PB⊥AE于B，PC⊥AF于C，
∴PB=PC，
在Rt△PBM和Rt△PCN中，
，
∴Rt△PBM≌Rt△PCN，
∴BM=CN；
（2）AM+CN=AC，
理由如下：在Rt△PBA和Rt△PCA中，
，
∴Rt△PBA≌Rt△PCA，
∴AB=AC，
∴AM+CN=AM+BM=AB=AC，
故答案为：AM+CN=AC；
（3）∵AC：PC=2：1，PC=4，
∴AC=8，
∵PB⊥AE，PC⊥AF，
∴∠ABP=∠ACP=90°，
∴∠MAN+∠BPC=180°，又∵∠MAN+∠MPN=180°，
∴∠MPB=∠NPC，
在△PBM和△PCN中，
，
∴△PBM≌△PCN，
∴四边形ANPM的面积=四边形ABPC的面积=×8×4×2=32．

八年级数学上第一次月考试题（五）
一、选择题（共8小题，每小题3分，共24分）
1．有下列长度的三条线段，能组成三角形的是（ ）
A．2cm，3cm，4cmB．1cm，4cm，2cmC．1cm，2cm，3cmD．6cm，2cm，3cm
2．以下是四位同学在钝角三角形ABC中画BC边上的高，其中画法正确的是（ ）
A．B．C．D．
3．正n边形每个内角的大小都为108°，则n=（ ）
A．5B．6C．7D．8
4．如图，某同学把一块三角形的玻璃打碎成了三块，现在要到玻璃店去配一块完全一样的玻璃，那么最省事的办法是（ ）
A．带①去 B．带②去 C．带③去 D．带①和②去

5．若一个三角形三个内角度数的比为2：3：7，那么这个三角形是（ ）
A．钝角三角形 B．锐角三角形 C．直角三角形 D．等边三角形
6．工人师傅常用角尺平分一个任意角，做法是：如图在∠AOB的边OA、OB上分别取OM=ON，移动角尺，使角尺的两边相同的刻度分别与M、N重合，得到∠AOB的平分线OP，做法中用到三角形全等的判定方法是（ ）
A．SSS B．SAS C．ASA D．HL
7．如图，在△ABC中，已知点D，E，F分别为BC，AD，AE的中点，且S△ABC=4cm2，则阴影部分面积S=（ ）cm2．
A．1B．2C．3D．4
8．如图，把△ABC纸片沿DE折叠，当点A落在四边形BCDE内部时，则∠A与∠1+∠2之间有一种数量关系始终保持不变．请试着找一找这个规律，你发现的规律是（ ）
A．∠A=∠1+∠2 B．2∠A=∠1+∠2 C．3∠A=2∠1+∠2 D．3∠A=2（∠1+∠2）
二、填空题（每题3分，共18分）．
9．如图，为了使木门不变形，木工师傅在木门上加钉了一根木条，这样是利用三角形的 ．

10．在△ABC中，∠A=80°，∠B=52°，则∠C= ．
11．如图，已知△ABC的两条高AD、BE交于F，AE=BE，若要运用“HL”说明△AEF≌△BEC，还需添加条件： ．
12．如图，点D在△ABC边BC的延长线上，CE平分∠ACD，∠A=80°，∠B=40°，则∠ACE的大小是 度．
13．AD是△ABC的中线，DE=DF．下列说法：①CE=BF；②△ABD和△ACD面积相等；③BF∥CE；④△BDF≌△CDE．其中正确的有 （写正确的序号）

14．如图，在△ABC中，∠A=α，∠ABC的平分线与∠ACD的平分线交于点A1，得∠A1，∠A1BC的平分线与∠A1CD的平分线交于点A2，得∠A2，…，∠A2013BC的平分线与∠A2013CD的平分线交于点A2014，得∠A2014CD，则∠A2014= ．
三、解答题（每题5分，共25分）．
15．（5分）作图，已知∠AOB，求作∠AOB的角平分线OM．（不写作法，保留作图痕迹）
16．（5分）如图，已知△EFG≌△NMH，∠F与∠M 是对应角．
（1）写出相等的线段与相等的角；
（2）若EF=2.1cm，FH=1.1cm，HM=3.3cm，求MN和HG的长度．
17．（5分）已知，如图OA=OC，OB=OD，∠B=23°，求∠D的度数．
18．（5分）等腰三角形的周长为13cm，其中一边长为3cm，求另两边的长．
19．（5分）如图，C岛在A岛的北偏东50°的方向，B岛在A岛的北偏东80°的方向，C岛在B 岛的北偏西40°方向．从C岛看A、B两岛的视角∠ACB是多少度？

四、解答题（每题6分，共18分）．
20．（6分）如图，在△ABC中，D是BC上一点，∠1=∠2，∠3=∠4，∠BAC=63°，求∠DAC的度数．
21．（6分）已知，如图，BC上有两点D、E，且BD=CE，AD=AE，∠1=∠2，求证：AB=AC．
22．（6分）已知：BE⊥CD于E，BE=DE，BC=DA，
（1）求证：△BEC≌△DEA；
（2）求证：BC⊥FD．

五、解答题（第23题7分，第24题8分，共15分）．
23．（7分）如图，AC⊥BC，DC⊥EC，AC=BC，DC=EC，图中AE、BD有怎样的关系（数量关系和位置关系）？并证明你的结论．
24．（8分）已知：∠MON=40°，OE平分∠MON，点A、B、C分别是射线OM、OE、ON上的动点（A、B、C不与点O 重合），连接AC交射线OE于点D．设∠OAC=x°．
（1）如图1，若AB∥ON，则
①∠ABO的度数是 ；
②当∠BAD=∠ABD时，x= ；当∠BAD=∠BDA时，x= ．
（2）如图2，若AB⊥OM，则是否存在这样的x的值，使得△ADB中有两个相等的角？若存在，求出x的值；若不存在，说明理由．

八年级（上）第一次月数学试卷五参考答案
一、1． A．2．B．3． A．4．C．5． A．6． A．7． A．8． B．
二、9．稳定性．10． 48°．11． AF=BC．12． 6013．①②③④．14． °．
三、15．解：如图所示，射线OM即为所求：
16．解：（1）∵△EFG≌△NMH，∠F与∠M是对应角，
∴EF=NM，EG=NH，FG=MH，∠F=∠M，∠E=∠N，∠EGF=∠NHM，
∴FH=GM，∠EGM=∠NHF；
（2）∵EF=NM，EF=2.1cm，∴MN=2.1cm；
∵FG=MH，FH+HG=FG，FH=1.1cm，HM=3.3cm，∴HG=FG﹣FH=HM﹣FH=3.3﹣1.1=2.2cm．
17．解：在△AOB和△COD中，
，
∴△AOB≌△COD，∴∠D=∠B，∵∠B=23°，∴∠D=23°
18．解：当长是3cm的边是底边时，三边为3cm，5cm，5cm，等腰三角形成立；
当长是3cm的边是腰时，底边长是：13﹣3﹣3=7cm，而3+3＜7，不满足三角形的三边关系．
故另两边的长是：5cm，5cm．
19．解：由题意得：∠DAC=50°，∠DAB=80°，∠CBE=40°，
过C作CF∥AD，
∵AD∥EB，∴CF∥EB，∴∠2=∠EBC=40°，
∵AD∥CF，∴∠1=∠DAC=50°，∴∠ACB=∠1+∠2=90°．
四、20．解：∵∠4=∠1+∠2，∠3=∠4，∠1=∠2，∠BAC=63°，∴∠3=∠1+∠2=2∠2，
∵∠BAC+∠2+∠3=180°，即3∠2+63°=180°，∴∠2=39°，
∴∠DAC=∠BAC﹣∠1=63°﹣39°=24°．
21．证明：∵BD=CE，∴BD+DE=CE+DE，即BE=CD，
在△ABE和△ACD中，
，
∴△ABE≌△ACD（SAS），∴AB=AC．
22．证明：（1）∵BE⊥CD，∴∠BEC=∠DEA=90°，∴在Rt△BEC与Rt△DEA中，
，
∴△BEC≌△DEA（HL）；
（2）∵由（1）知，△BEC≌△DEA，∴∠B=∠D．
∵∠D+∠DAE=90°，∠DAE=∠BAF，∴∠BAF+∠B=90°，即DF⊥BC．
五、23．解：结论：AE=BD，AE⊥BD，
理由：如图，设AC交BD于N，AE交BD于O，
∵∠ACB=∠DCE=90°，∠ACD=∠ACD，∴∠DCB=∠ECA，
在△DCB和△ECA中，
，
∴△DCB≌△ECA（SAS），∴∠A=∠B，BD=AE
∵∠AND=∠BNC，∠B+∠BNC=90°∴∠A+∠AND=90°，
∴∠AON=90°，∴BD⊥AE．
24．解：（1）①∵∠MON=40°，OE平分∠MON∴∠AOB=∠BON=20°
∵AB∥ON∴∠ABO=20°
②∵∠BAD=∠ABD∴∠BAD=20°∵∠AOB+∠ABO+∠OAB=180°∴∠OAC=120°
∵∠BAD=∠BDA，∠ABO=20°∴∠BAD=80°∵∠AOB+∠ABO+∠OAB=180°∴∠OAC=60°
故答案为：①20 ②120，60
（2）①当点D在线段OB上时，
∵OE是∠MON的角平分线，∴∠AOB=∠MON=20°，
∵AB⊥OM，∴∠AOB+∠ABO=90°，∴∠ABO=70°，
若∠BAD=∠ABD=70°，则x=20
若∠BAD=∠BDA=（180°﹣70°）=55°，则x=35
若∠ADB=∠ABD=70°，则∠BAD=180°﹣2×70°=40°，∴x=50
②当点D在射线BE上时，因为∠ABE=110°，且三角形的内角和为180°，
所以只有∠BAD=∠BDA，此时x=125．
综上可知，存在这样的x的值，使得△ADB中有两个相等的角，
且x=20、35、50、125．
八年级数学上第一次月考试题（六）
一．选择题（每小题3分，共36分）
1．若三角形的三边长分别为3，4，x，则x的值可能是（ ）
A．1B．6C．7D．10
2．△ABC中，∠A=60°，∠C=70°，则∠B的度数是（ ）
A．50°B．60°C．70°D．90°
3．如图，△BAC的外角∠CAE为120°，∠C=80°，则∠B为（ ）
A．60°B．40°C．30°D．45°
4．如图，工人师傅砌门时，常用木条EF固定长方形门框ABCD，使其不变形，这样做的根据是（ ）
A．两点之间的线段最短 B．长方形的四个角都是直角
C．长方形是轴对称图形 D．三角形有稳定性

5．不一定在三角形内部的线段是（ ）
A．三角形的角平分线B．三角形的中线
C．三角形的高D．以上皆不对
6．若a、b、c为△ABC的三边长，且满足|a﹣4|+=0，则c的值可以为（ ）
A．5B．6C．7D．8
7．一个正多边形的内角和为540°，则这个正多边形的每一个外角等于（ ）
A．60°B．72°C．90°D．108°
8．如图，下列条件中，不能证明△ABC≌△DCB的是（ ）
A．AB=DC，AC=DBB．AB=DC，∠ABC=∠DCB
C．BO=CO，∠A=∠DD．AB=DC，∠DBC=∠ACB
9．小明不慎将一块三角形的玻璃摔碎成如图所示的四块（即图中标有1、2、3、4的四块），你认为将其中的哪一些块带去，就能配一块与原来一样大小的三角形？应该带（ ）
A．第1块B．第2块C．第3块D．第4块
10．下列各选项中的两个直角三角形不一定全等的是（ ）
A．两条直角边对应相等的两个直角三角形 B．两个锐角对应相等的两个直角三角形
C．斜边和一条直角边对应相等的两个直角三角形
D．有一个锐角及这个锐角的对边对应相等的两个直角三角形全等
11．如图，△ACB≌△A′CB′，∠BCB′=30°，则∠ACA′的度数为（ ）
A．20°B．30°C．35°D．40°

12．如图，△ABC≌△EBD，AB=3cm，BD=5cm，则CE的长度为（ ）
A．3cmB．5cmC．8cmD．2cm
二．填空题（每小题4分，共32分）
13．在△ABC中，若AB=5，BC=2，且AC的长为奇数，则AC= ．
14．如果一个多边形的内角和为1080°，则它是 边形．
15．在直角三角形中，两个锐角的差为40°，则这两个锐角的度数分别为 ．
16．已知图中的两个三角形全等，则∠α的度数是 ．

17．如图，已知AD平分∠BAC，要使△ABD≌△ACD，根据“SAS”，需要添加的条件是 ．
18．如图，△ABC的角平分线AD交BD于点D，∠1=∠B，∠C=66°，则∠BAC的度数是 ．

19．如图，在△ABC中，已知∠1=∠2，BE=CD，AB=5，AE=2，则CE= ．
20．如图，△ADB≌△ACE，∠E=40°，∠C=25°，则∠DAB= ．
三．解答题（5小题，共52分）
21．（10分）一个多边形的内角和比外角和的3倍多180°，则它是几边形？
22．（10分）如图所示，已知AD，AE分别是△ADC和△ABC的高和中线，AB=6cm，AC=8cm，BC=10cm，∠CAB=90°．试求：
（1）AD的长；（2）△ABE的面积；（3）△ACE和△ABE的周长的差．
23．（10分）如图，已知△ABC≌△DEF，∠A=30°，∠B=50°，BF=2，求∠DFE的度数和EC的长．
24．（10分）已知：如图，点B、F、C、E在同一条直线上，AB∥DE，∠A=∠D，BF=EC．求证：AC=DF．
25．（12分）如图，两根旗杆AC，BD相距10米，旗杆AC高3米，且AC⊥AB，BD⊥AB，一同学从B点出发向A点走去，当他走到点M时，发现自己刚好走了3米，此时他仰望旗杆的顶点C，D，又发现两条视线CM=DM．
（1）求旗杆BD的高为多少米？
（2）两条视线CM，DM有怎样的位置关系？请说明理由．

八年级（上）第一次月考数学试卷六参考答案
一． 1． B．2． A．3． B．4． D．5． C．6． A．7． B．8． D．9． B．10． B．11． B．12． D．
二．源:]13． 5．14．八．15． 65°，25°．16． 50°．17． AB=AC．18． 76°19． 3．20． 115°．
三．21．解：设多边形的边数为n，
根据题意得：（ n﹣2）×180°﹣360°×3=180°，
解得：n=9．
答：它是九边形．
22．解：∵∠BAC=90°，AD是边BC上的高，
∴AB•AC=BC•AD，
∴AD===4.8（cm），即AD的长度为4.8cm；
（2）如图，∵△ABC是直角三角形，∠BAC=90°，AB=6cm，AC=8cm，
∴S△ABC=AB•AC=×6×8=24（cm2）．
又∵AE是边BC的中线，
∴BE=EC，
∴BE•AD=EC•AD，即S△ABE=S△AEC，
∴S△ABE=S△ABC=12（cm2）．
∴△ABE的面积是12cm2．
（3）∵AE为BC边上的中线，
∴BE=CE，
∴△ACE的周长﹣△ABE的周长=AC+AE+CE﹣（AB+BE+AE）=AC﹣AB=8﹣6=2（cm），即△ACE和△ABE的周长的差是2cm．
23．解：∵∠A=30°，∠B=50°，
∴∠ACB=180°﹣∠A﹣∠B=180°﹣30°﹣50°=100°，
∵△ABC≌△DEF，
∴∠DFE=∠ACB=100°，EF=BC，
∴EF﹣CF=BC﹣CF，即EC=BF，
∵BF=2，
∴EC=2．
24．证明：∵AB∥DE（已知），
∴∠ABC=∠DEF（（两直线平行，内错角相等），
∵BF=EC（已知），
∴BF+FC=EC+CF，
即BC=EF，
在△ABC和△DEF中，
，
∴△ABC≌△DEF（AAS），
∴AC=DF（全等三角形对应边相等）．
25．解：（1）∵AC⊥AB，BD⊥AB，
∴∠A=∠B=90°，
在Rt△ACM和Rt△BMD中，
，
∴Rt△ACM≌Rt△BMD（HL），
∴AM=BD，
∴AM=AB﹣BM=7，
∴BD=AM=7；
（2）CM⊥DM，
理由：∵Rt△ACM≌Rt△BMD，
∴∠C=∠BMD，
∵∠C+∠AMC=90°，
∴∠BMD+∠AMC=90°，
∴∠CMD=90°，
∴CM⊥DM．

八年级数学上第一次月考试题（七）
一、选择题（每小题3分，共30分）
1．有4cm和6cm的两根小棒，请你再找一根小棒，并以这三根小棒为边围成一个三角形，下列长度的小棒可选的是（ ）
A．1cmB．2cmC．7cmD．10cm
2．若一个多边形的每一个内角都等于108°，则它是（ ）
A．四边形B．五边形C．六边形D．八边形
3．一个三角形三个内角的度数之比为2：3：7，这个三角形一定是（ ）
A．等腰三角形B．直角三角形C．锐角三角形D．钝角三角形
4．如图，AD是△ABC的中线，那么下列结论中错误的是（ ）
A．BD=CD B．BC=2BD=2CD C．S△ABD=S△ACD D．△ABD≌△ACD
5．如图，BE、CF是△ABC的角平分线，∠ABC=80°，∠ACB=60°，EB、CF相交于D，则∠CDE的度数是（ ）
A．130°B．70°C．80°D．75°

6．如图．从下列四个条件：①BC=B′C，②AC=A′C，③∠A′CA=∠B′CB，④AB=A′B′中，任取三个为条件，余下的一个为结论，则最多可以构成正确的结论的个数是（ ）
A．1个B．2个C．3个D．4个
7．AD是△ABC的角平分线，过点D作DE⊥AB于E，DF⊥AC于F，则下列结论不一定正确的是（ ）
A．DE=DFB．BD=CDC．AE=AFD．∠ADE=∠ADF

8．如图，点B、C、E在同一条直线上，△ABC与△CDE都是等边三角形，则下列结论不一定成立的是（ ）
A．△ACE≌△BCDB．△BGC≌△AFCC．△DCG≌△ECFD．△ADB≌△CEA
9．要测量河两岸相对的两点A，B的距离，先在AB的垂线BF上取两点C，D，使CD=BC，再定出BF的垂线DE，使A，C，E在一条直线上（如图所示），可以说明△EDC≌△ABC，得ED=AB，因此测得ED的长就是AB的长，判定△EDC≌△ABC最恰当的理由是（ ）
A．边角边B．角边角C．边边边D．边边角
10．如图，在△ABC中，∠C=90°，点D在AB上，BC=BD，DE⊥AB交AC于点E，△ABC的周长为12，△ADE的周长为6，则BC的长为（ ）
A．3B．4C．5D．6
二、填空题（每小题3分，共15分）
11．△ABC中，∠A=32°，∠B=76°，则与∠C相邻的外角是 °．
12．一个多边形的内角和是它外角和的8倍，则这个多边形是 边形．
13．如图，AB=DC，请补充一个条件： 使△ABC≌△DCB．（填其中一种即可）

14．如图，在△ABC中，AB=AC，∠BAC=90°，AE是过A点的一条直线，CE⊥AE于E，BD⊥AE于D，DE=4cm，CE=2cm，则BD= ．
15．如图，已知△ABC的周长是21，OB，OC分别平分∠ABC和∠ACB，OD⊥BC于D，且OD=3，△ABC的面积是 ．
三、解答题（共9小题，共75分）
16．（6分）如图，在△ABC中，∠BAC是钝角，完成下列画图．（不写作法保留作图痕迹）
（1）△ABC的角平分线AD；（2）AC边上的中线BE；（3）AC边上的高BF．
17．（7分）如图，AC=DF，AD=BE，BC=EF．求证（1）△ABC≌△DEF； （2）AC∥DF．
18．（8分）（1）已知等腰三角形的一边长等于8cm，一边长等于9cm，求它的周长；
（2）等腰三角形的一边长等于6cm，周长等于28cm，求其他两边的长．
19．（8分）如图，CE是△ABC的外角∠ACD的平分线，且CE交BA的延长线于点E，∠B=30°，∠E=20°，求∠ACE和∠BAC的度数．
20．（8分）已知，如图，在△ABC中，AD，AE分别是△ABC的高和角平分线，若∠B=30°，∠C=50°，求∠DAE的度数．
21．（9分）如图，△ABC的外角平分线BP、CP相交于点P．求证：点P在∠A的平分线上．
22．（9分）如图，在Rt△ABC中，∠BAC=90°，AC=2AB，点D是AC的中点，将一块锐角为45°的直角三角板ADE如图放置，使三角板斜边的两个端点分别与A、D重合，连接BE、EC．试猜想线段BE和EC有怎样的数量关系，并证明你的猜想．
23．（10分）如图，已知△ABC中，AB=6cm，∠B=∠C，BC=4cm，点D为AB的中点．若点P在线段BC上以1cm/s的速度由点B向点C运动，同时，点Q在线段CA上由点C向点A运动．
（1）若点Q的运动速度与点P的运动速度相等，经过1秒后，△BPD与△CQP是否全等，请说明理由；
（2）若点Q的运动速度与点P的运动速度不相等，当点Q的运动速度为多少时，能够使△BPD与△CQP全等？
24．（10分）如图1，在平面直角坐标系中，A（﹣2，0），B（0，3），C（3，0），D（0，2）．
（1）求证：AB=CD且AB⊥CD；
（2）如图2，以A为直角顶点在第二象限内作等腰直角三角形ABE，过点E作EF⊥x轴于点F，求点F的坐标；
（3）如图3，若点P为y轴正半轴上一动点，以AP为直角边作等腰直角三角形APQ，点Q在第一象限，∠APQ=90°，QR⊥x轴于点R，当点P运动时，OP﹣QR的值是否发生变化？若不变，求出其值；若变化，请说明理由．

八年级（上）第一次月考数学试卷七参考答案
一、1． C．2． B．3． D．4． D．5． B．6． B．7． B．8． D．9． B．10． A．
二、11． 108．12．十八．13． AC=BD．14． 6cm．15． 31.5．
三、
16．
解：．
（1）AD是△ABC的角平分线．（2）BE是AC边上的中线．（3）BF是AC边上的高．
17．证明：（1）∵AD=BE，∴AD+DB=BE+DB，∴AB=DE，
在△ABC和△DEF中
∴△ABC≌△DEF（SSS）；
（2）∵△ABC≌△DEF，∴∠A=∠EDF，∴AC∥DF．
18．解：（1）8cm是腰长时，三角形的三边分别为8cm、8cm、9cm，
能组成三角形，
周长=8+8+9=25cm，
8cm是底边时，三角形的三边分别为8cm、9cm、9cm，
能组成三角形，
周长=8+9+9=26cm，
综上所述，周长为25cm或26cm；
（2）6cm是腰长时，其他两边分别为6cm，16cm，
∵6+6=12＜16，∴不能组成三角形，
6cm是底边时，腰长为×（28﹣6）=11cm，
三边分别为6cm、11cm、11cm，
能组成三角形，
所以，其他两边的长为11cm、11cm．
19．解：∵∠B=30°，∠E=20°，∴∠ECD=∠B+∠E=50°，
∵CE平分∠ACD，∴∠ACE=∠ECD=50°，∠ACD=2∠ECD=100°，
∵∠BAC=∠ACD﹣∠B=100°﹣30°=70°．
20．解：∵∠BAC+∠B+∠C=180°，
而∠B=30°，∠C=50°，∴∠BAC=180°﹣30°﹣50°=100°，
∵AE是△ABC的角平分线，∴∠EAC=∠BAC=50°
又∵AD为高线，∴∠ADC=90°，而∠C=50°，
∴∠DAC=180°﹣90°﹣50°=40°，∴∠DAE=∠EAC﹣∠DAC=50°﹣40°=10°．
21．解：如图，过点P作PM⊥AD、PN⊥BC、PQ⊥AE，垂足分别为M、N、Q，
∵∠ABC、∠ACB的外角平分线BP、CP交于点P．∴PM=PN，PQ=PN，∴PM=PQ，
∴P在∠A的平分线上．
22．解：数量关系为：BE=EC，位置关系是：BE⊥EC．
证明如下：
∵△AED是直角三角形，∠AED=90°，且有一个锐角是45°，∴∠EAD=∠EDA=45°，
∴AE=DE，
∵∠BAC=90°，∴∠EAB=∠EAD+∠BAC=45°+90°=135°，∠EDC=∠ADC﹣∠EDA=180°﹣45°=135°，
∴∠EAB=∠EDC，
∵D是AC的中点，∴AD=CD=AC，
∵AC=2AB，∴AB=AD=DC，
∵在△EAB和△EDC中
，
∴△EAB≌△EDC（SAS），
∴EB=EC，且∠AEB=∠DEC，∴∠BEC=∠DEC+∠BED=∠AEB+∠BED=90°，∴BE⊥EC．
23．解：（1）全等，理由如下：
∵t=1秒，∴BP=CQ=1×1=1厘米
∵AB=6cm，点D为AB的中点，∴BD=3cm．
又∵PC=BC﹣BP，BC=4cm，∴PC=4﹣1=3cm，∴PC=BD．
∵∠B=∠C，∴△BPD≌△CPQ；
（2）∵vP≠vQ，∴BP≠CQ，
又∵△BPD≌△CPQ，∠B=∠C，则BP=CP=2，BD=CQ=3，
∴点P，点Q运动的时间为：t=2秒，∴vQ=1.5cm/s；
24．解：（1）证明：如图1，
延长CD交AB于点E．
∵A（﹣2，0），B（0，3），C（3，0），D（0，2），∴OA=OD=2，OB=OC=3．
∵∠AOB=90°，∠DOC=90°，∴∠AOB=∠DOC．
在△AOB和△DOC中．
，
∴△AOB≌△DOC（SAS），∴∠ABO=∠DCO．∠BAO=∠CDO，AB=CD．
∵∠BDG=∠CDO，∴∠BAO=∠BDG．
∵∠BAO+∠ABO=90°，∴∠BDG+∠ABO=90°，∴∠BGD=90°，∴AB⊥CD；
（2）∵△ABE是等腰直角三角形，
∴AE=AB，∠EAB=90°，∴∠FAE+∠BAO=90°．
∵EF⊥x轴，∴∠EFA=90°，
∴∠AEF+∠FAE=90°，∴∠AEF=∠OAB．
∵∠AOB=90°，∴∠EFA=∠AOB．
在△AEF和△BAO中，
，
∴△AEF≌△BAO（AAS），∴AF=BO=3，∴OF=2+3=5，∴F（﹣5，0）．
答：F的坐标为（﹣5，0）；
（3）OP﹣QR的值不变．
理由：如图3，作QH⊥OP于H，∴∠PHQ=∠QHO=90°，∴∠HPQ+∠HQP=90°．
∵△APQ是等腰直角三角形，∴PA=PQ，∠APQ=90°，∴∠APO+∠OPQ=90°．
∴∠APO=∠PQH．
∵∠AOP=∠POR=90°，∴∠AOP=∠PHQ．
在△AOP和△PHQ中，
，
∴△AOP≌△PHQ（AAS），∴AO=PH．
∵QR⊥x轴，∴∠QRA=90°．∴∠QRA=∠POR=∠QHO=90°，∴四边形FORQ是矩形，
∴QR=HO．∴OP﹣QR=OP﹣OF=PH，∴OP﹣QR=OA=2是定值．

八年级数学上第一次月考试题（八）
一、选择题:（本大题12个小题，每小题4分，共48分）
1.下列哪组线段的长能够组成三角形（ ）
1、2、3 B.2、3、4 C.4、5、9 D.4、4、8.
2.如图，王师傅用4根木条钉成一个四边形木架，要使这个木架不变形，他至少要再订上木条的根数是（ ）
A.0. B.1. C.2. D3.
3.将一副常规的三角尺如图放置，则图中∠AOB的度数是（ ）
A.75°. B. 95°. C. 105°. D.120

4．下列说法错误的是（ ）
A.一个三角形中至少有一个角不少于60° B.三角形的中线不可能在三角形的外部.
C.三角形的中线把三角形的面积平均分成相等的两部分 D.直角三角形只有一条高.
5．如果一个多边形的每一个外角都是45°，那么这个多边形的内角和是（ ）
A.540°. B.720°. C. 1080°. D.1260°.
6.下列说法： ①全等三角形的形状相同、大小相等 ②全等三角形的对应边相等、对应角相等 ③面积相等的两个三角形全等 ④全等三角形的周长相等其中正确的说法为（ ）
A.①②③④ B. ①②③ C. ②③④ D. ①②④
7.若一个三角形的三条高的交点恰是三角形的一个顶点，那么这个三角形是（ ）
A.锐角三角形 B.钝角三角形 C.直角三角形 D.以上都 不对
8.已知在ΔABC中，AB=AC,周长为24，AC边上的中线BD把ΔABC分成周长差为6的两个三角形，则ΔABC各边的长分别变为______。
A.10、10、4 B.6、6、12 C.4、5、10 D.以上都不对
9．在ΔABC和ΔDEF中，已知∠C =∠D, ∠B=∠E,要判断这两个三角形全等，还需添加条件（ ）
A. AB=ED. B.AB=FD. C.AC=FD. D. ∠A =∠F.
10．如图，点P是AB上任一点，∠ABC=∠ABD,从下列各条件中补充一个条件，
不一定能推出ΔAPC≌ΔAPD.的是( )
11题图
12题图
BC=BD. B. ∠ACB=∠ADB. C.AC=AD. D. ∠CAB=∠DAB
10题图
11．已知ΔABC是等边三角形，点D、E分别在AC、BC边上，且AD=CE,AE与BD交于点F,则∠AFD的度数为( )
A.60° B.45° C.75° D. 70°
12．如图ΔABC中，∠B =∠C,BD=CF,BE=CD, ∠EDF=α，则下列结论正确的是（ ）
A.2α+∠A=90° B. .2α+∠A=180° C.α+∠A=90° D.α+∠A=180
二、填空题（每小题3分,共24分）
13题图
13．如图，将一张直角三角形纸片剪去直角后，得到一个四边形，则∠1+∠2=___ ___。

14．ΔABC中，∠A=60°，∠ABC和∠ACB的平分线相交于点P，则∠BPC=____
15.在ΔABC中，∠C=90°，AD平分∠CAB,交BC与D，过点D作DE⊥AB于E，BC=8cm,BD=5cm,则DE=______。
16.如图所示，已知AB=DC,要得到ΔABC≌ΔDCB，还需加一个条件是 。(一个即可)
17．如图，B、C、E共线AB⊥BE,DE⊥BE,AC⊥DC,AC=DC，又AB=2cm，DE=1cm，则BE=______。
18.已知在ΔABC中，AD=BD，AC=5，BD=3,H是高AD和BE的交点，则线段BH的长度为______。
三、完成下列各题（每小题7分，共14分）
19. 如图，在ΔABC中，∠C=∠ABC=2∠A，BD⊥AC于D，求∠DBC的度数。
20.如图：已知AB=AD，BC=DC,求证∠B=∠D
四．解答及证明题（每小题10分共40分）
21．如图，已知AE⊥BC,AD平分∠BAE，∠ADB=110°.求∠B的度数。
22、如图，AC=DF，AD=BE，BC=EF.求证(1) △ABC≌△DEF ； (2) AC∥DF.
22题图

23、如图所示,点B、F、C、E在同一条直线上，AB∥DF，AC∥DE，AC=DE，FC与BE相等吗？请说明理由.
23题图




24．如图, 在ΔABC与ΔDCB 中, AC与BD 交于点E，且,∠A=∠D,AB=DC.
⑴．求证：ΔABE≌ΔDCE
24题图
⑵．当∠AEB=70°时，求∠EBC的度数。

五，（每题12分，共24分）
25. 在ΔABC中，∠ABC的平分线与∠ACB的外角∠ACE的平分线相交于点D。
⑴．若∠ABC=60°，∠ACB=40°,求∠A和∠D的度数。
⑵．由⑴小题的计算结果，猜想，∠A和∠D有什么数量关系，并加以证明。
25题图
26.如图（1）在ΔABC中，∠ACB=90°，AC=BC,直线MN经过点C,且AD⊥MN于点D,BE⊥MN于点E。
（1）求证：①ΔADC≌ΔCEB ②DE=AD+BE
（2）当直线MN绕点C旋转到图（2）的位置时，DE、AD、BE 有怎样的关系？并加以证明。
第26题图




八年级数学八参考答案
一、选择题
1.B 2.B 3.C 4 .D 5. C 6 .D 7 C 8 .A 9. C 10 C 11A 12B
二、填空题
13.270° 14.120° 15. 3cm. 16. ∠ABC= ∠DCB或AC=BD 17. 3cm. 18. 5cm
三、
19.解：设 ∠A =x,则∠C=∠ABC =2x,又x+2x+2x=180,得x=36, ∠C =72°∵BD⊥AC
∴∠DBC=18°
20，证明：连接AC,在 ABC和 ADC中.
∴ABC≌ ADC ∴∠
21．∠B=50°
22.略。23略
24. ⑴ 在 ABE和 DCE中.
∴ABE≌ DCE （AAS）
⑵∠EBC=35°
25. ∠A=80°，∠D=40°
∠A=2∠D
证明：∵CD 平分∠ACE ∴∠ACE=2∠DCE又∠DCE=∠D+∠DBC∴2∠DCE=2∠D+2∠DBC ∵BD平分∠ABC∴∠ABC=2∠DBC即∠ACE=2∠D+∠ABC而∠ACE=∠A+∠ABC
∴2∠D=∠A
26. 证出ΔADC≌ΔCEB得
由 ΔADC≌ΔCEB得AD=CE DC=BE ∴DC+CE=AD+BE即DE=AD+BE
（2）DE=AD-BE
易证ΔADC≌ΔCEB ∴AD=CE CD=BE 又DE=CE-CD∴DE=AD-BE