【中考特训】贵州省铜仁市中考数学历年真题汇总 卷（Ⅲ）（含答案及解析）

这是一份【中考特训】贵州省铜仁市中考数学历年真题汇总 卷（Ⅲ）（含答案及解析），共33页。试卷主要包含了如图，下列条件中不能判定的是，如图，，下列语句中，不正确的是等内容，欢迎下载使用。

考生注意：
1、本卷分第I卷（选择题）和第Ⅱ卷（非选择题）两部分，满分100分，考试时间90分钟
2、答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上
3、答案必须写在试卷各个题目指定区域内相应的位置，如需改动，先划掉原来的答案，然后再写上新的答案；不准使用涂改液、胶带纸、修正带，不按以上要求作答的答案无效。
第I卷（选择题 30分）
一、单选题（10小题，每小题3分，共计30分）
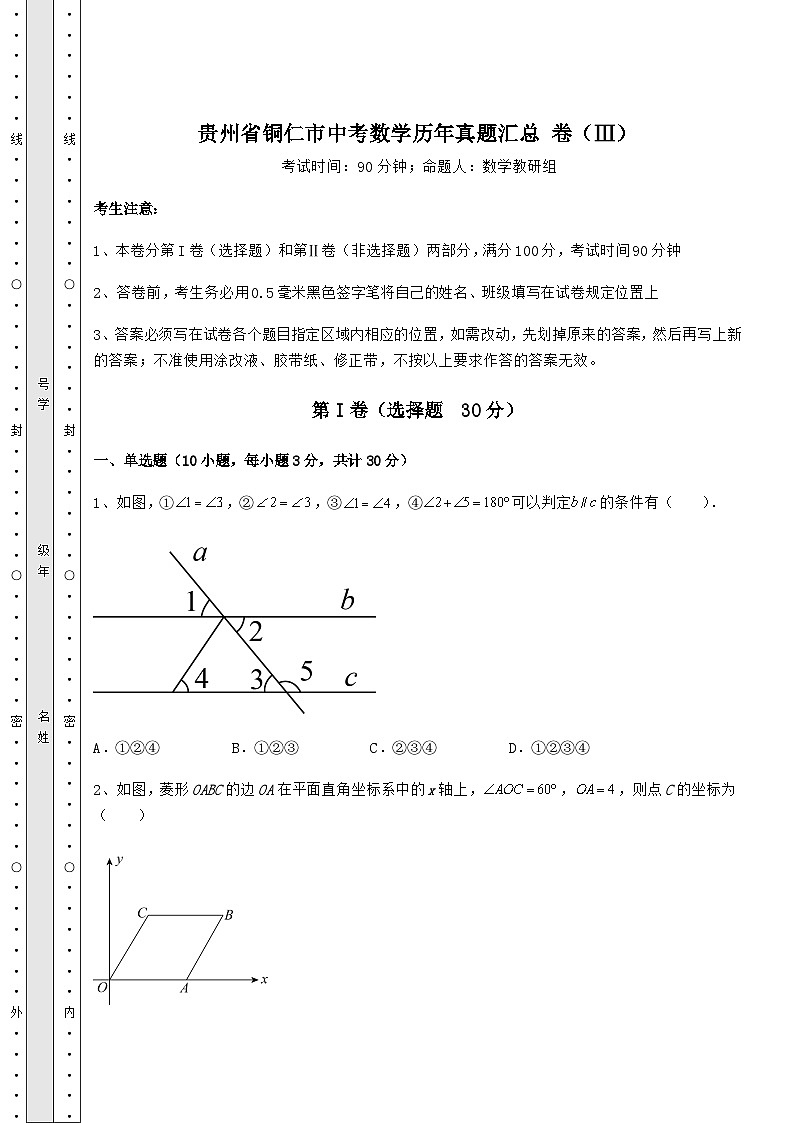
1、如图，①，②，③，④可以判定的条件有（ ）．
A．①②④B．①②③C．②③④D．①②③④
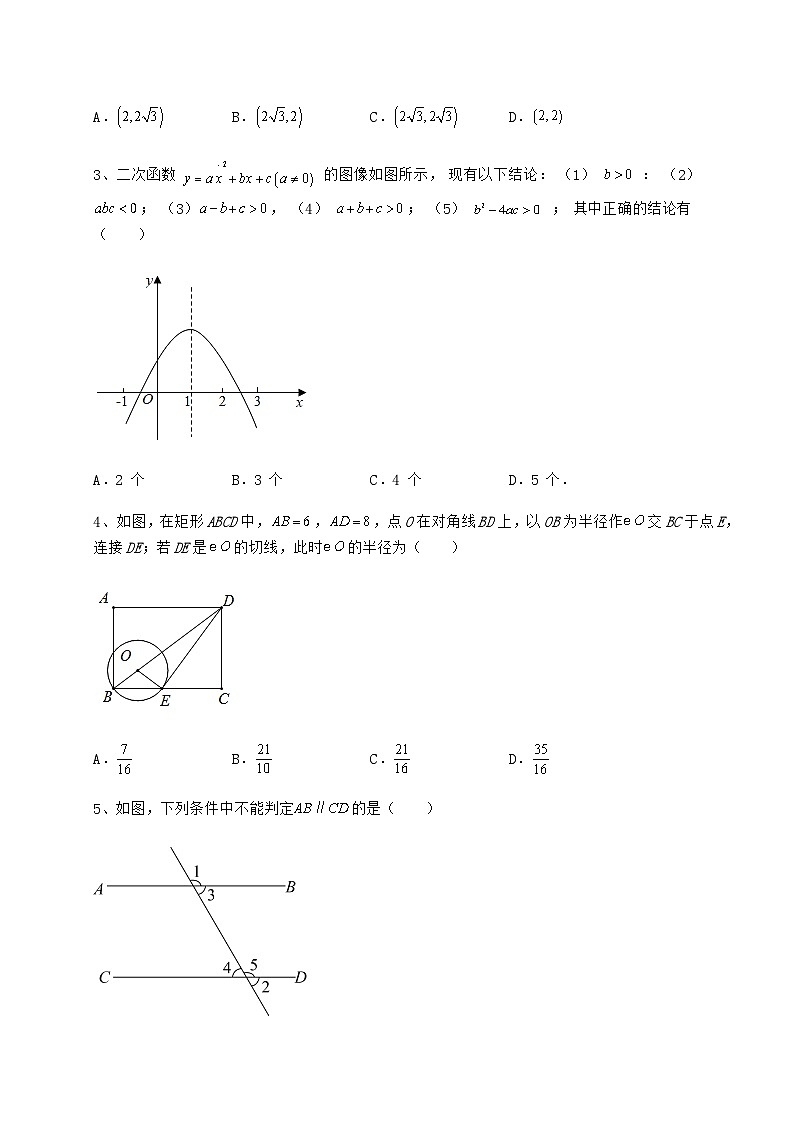
2、如图，菱形OABC的边OA在平面直角坐标系中的x轴上，，，则点C的坐标为（ ）
A．B．C．D．
3、二次函数 的图像如图所示， 现有以下结论： （1） ： （2） ； （3）， （4） ； （5） ； 其中正确的结论有（ ）
A．2 个B．3 个C．4 个D．5 个．
4、如图，在矩形ABCD中，，，点O在对角线BD上，以OB为半径作交BC于点E，连接DE；若DE是的切线，此时的半径为（ ）
A．B．C．D．
5、如图，下列条件中不能判定的是（ ）
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 内 · · · · · · ○ · · · · · ·
号学级年名姓
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 外 · · · · · · ○ · · · · · ·
A．B．C．D．
6、如图，在中，D是延长线上一点，，，则的度数为（ ）
A．B．C．D．
7、如图，、是的切线，、是切点，点在上，且，则等于（ ）
A．54°B．58°C．64°D．68°
8、如图，点A，B，C在⊙O上，∠ACB=35°，则∠AOB的度数是（ ）
A．75°B．70°C．65°D．55°
9、下列语句中，不正确的是（ ）
A．0是单项式B．多项式的次数是4
C．的系数是D．的系数和次数都是1
10、下列图形中，能用，，三种方法表示同一个角的是（ ）
A．B．
C．D．
第Ⅱ卷（非选择题 70分）
二、填空题（5小题，每小题4分，共计20分）
1、如图，商品条形码是商品的“身份证”，共有13位数字．它是由前12位数字和校验码构成，其结构分别代表“国家代码、厂商代码、产品代码、和校验码”．
其中，校验码是用来校验商品条形码中前12位数字代码的正确性．它的编制是按照特定的算法得来的．其算法为：
步骤1：计算前12位数字中偶数位数字的和，即；
步骤2：计算前12位数字中奇数位数字的和，即；
步骤3：计算与的和，即；
步骤4：取大于或等于且为10的整数倍的最小数，即中；
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 内 · · · · · · ○ · · · · · ·
号学级年名姓
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 外 · · · · · · ○ · · · · · ·
步骤5：计算与的差就是校验码X，即．
如图，若条形码中被污染的两个数字的和是5，则被污染的两个数字中右边的数字是______．
2、如图，在平面直角坐标系xOy中，P为函数图象上一点，过点P分别作x轴、y轴的垂线，垂足分别为M，N．若矩形PMON的面积为3，则m的值为______．
3、∠AOB的大小可由量角器测得（如图所示），则∠AOB的补角的大小为_____度．
4、计算：______．
5、如图中给出了某城市连续5天中，每一天的最高气温和最低气温（单位：），那么最大温差是________．
三、解答题（5小题，每小题10分，共计50分）
1、如图，在平面直角坐标系中，，，．
（1）在图中作出关于轴的对称图形，并直接写出点的坐标；
（2）求的面积；
（3）点与点关于轴对称，若，直接写出点的坐标．
2、在平面直角坐标系xOy中，已知点A（1，0）和点B（5，0）．对于线段AB和直线AB外的一点C，给出如下定义：点C到线段AB两个端点的连线所构成的夹角∠ACB叫做线段AB关于点C的可视角，其中点C叫做线段AB的可视点．
（1）在点D（-2，2）、E（1，4）、F（3，-2）中，使得线段AB的可视角为45°的可视点是 ；
（2）⊙P为经过A，B两点的圆，点M是⊙P上线段AB的一个可视点.
① 当AB为⊙P的直径时，线段AB的可视角∠AMB为 度；
② 当⊙P的半径为4时，线段AB的可视角∠AMB为 度；
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 内 · · · · · · ○ · · · · · ·
号学级年名姓
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 外 · · · · · · ○ · · · · · ·
（3）已知点N为y轴上的一个动点，当线段AB的可视角∠ANB最大时，求点N的坐标．
3、计算：（x+2）（4x﹣1）+2x（2x﹣1）．
4、已知平行四边形的顶点、分别在其的边、上，顶点、在其的对角线上．

图1 图2
（1）如图1，求证：；
（2）如图2，若，，求的值；
（3）如图1，当，，求时，求的值．
5、已知：在四边形中，于E，且．
（1）如图1，求的度数；
（2）如图2，平分交于F，点G在上，连接，且．求证：；
（3）如图3，在（2）的条件下，，过点F作，且，若，求线段的长．
-参考答案-
一、单选题
1、A
【分析】
根据平行线的判定定理逐个排查即可．
【详解】
解：①由于∠1和∠3是同位角，则①可判定；
②由于∠2和∠3是内错角，则②可判定；
③①由于∠1和∠4既不是同位角、也不是内错角，则③不能判定；
④①由于∠2和∠5是同旁内角，则④可判定；
即①②④可判定．
故选A．
【点睛】
本题主要考查了平行线的判定定理，平行线的判定定理主要有：两条直线被第三条直线所截，如果同位角相等，那么这两条直线平行；如果内错角相等，那么这两条直线平行；如果同旁内角互补，那么这两条直线平行．
2、A
【分析】
如图：过C作CE⊥OA，垂足为E，然后求得∠OCE=30°，再根据含30°角直角三角形的性质求得OE，最后运用勾股定理求得CE即可解答.
【详解】
解：如图：过C作CE⊥OA，垂足为E，
∵菱形OABC，
∴OC=OA=4
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 内 · · · · · · ○ · · · · · ·
号学级年名姓
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 外 · · · · · · ○ · · · · · ·
∵，
∴∠OCE=30°
∵OC=4
∴OE=2
∴CE=
∴点C的坐标为.
故选A.
【点睛】
本题主要考查了菱形的性质、含30°直角三角形的性质、勾股定理等知识点，作出辅助线、求出OE、CE的长度是解答本题的关键.
3、C
【分析】
由抛物线的开口方向判断a与0的关系，由抛物线与y轴的交点判断c与0的关系，然后根据对称轴及抛物线与x轴交点情况进行推理，进而对所得结论进行判断．
【详解】
解：（1）∵函数开口向下，∴a＜0，∵对称轴在y轴的右边，∴，∴b＞0，故命题正确；
（2）∵a＜0，b＞0，c＞0，∴abc＜0，故命题正确；
（3）∵当x=-1时，y＜0，∴a-b+c＜0，故命题错误；
（4）∵当x=1时，y>0，∴a+b+c>0，故命题正确；
（5）∵抛物线与x轴于两个交点，∴b2-4ac＞0，故命题正确；
故选C．
【点睛】
本题考查了二次函数图象与二次函数系数之间的关系，会利用对称轴的范围求2a与b的关系，以及二次函数与方程之间的转换，根的判别式的熟练运用．
4、D
【分析】
设半径为r，如解图，过点O作，根据等腰三角形性质，根据四边形ABCD为矩形，得出∠C=90°=∠OFB，∠OBF=∠DBC，可证．得出，根据勾股定理，代入数据，得出，根据勾股定理在中，，即，根据为的切线，利用勾股定理，解方程即可．
【详解】
解：设半径为r，如解图，过点O作，
∵OB=OE，
∴，
∵四边形ABCD为矩形，
∴∠C=90°=∠OFB，∠OBF=∠DBC，
∴．
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 内 · · · · · · ○ · · · · · ·
号学级年名姓
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 外 · · · · · · ○ · · · · · ·
∴，
∵，
∴，
∴，
∴，
∴．
在中，，即，
又∵为的切线，
∴，
∴，
解得或0（不合题意舍去）．
故选D．
【点睛】
本题考查矩形性质，等腰三角形性质，圆的切线，勾股定理，一元二次方程，掌握矩形性质，等腰三角形性质，圆的切线性质，勾股定理，一元二次方程，矩形性质，等腰三角形性质，圆的半径相等，勾股定理，一元二次方程，是解题关键．
5、A
【分析】
根据平行线的判定逐个判断即可．
【详解】
解：A、∵∠1=∠2，∠1+∠3=∠2+∠5=180°，
∴∠3=∠5，
因为”同旁内角互补，两直线平行“，
所以本选项不能判断AB∥CD；
B、∵∠3=∠4，
∴AB∥CD，
故本选项能判定AB∥CD；
C、∵，
∴AB∥CD，
故本选项能判定AB∥CD；
D、∵∠1=∠5，
∴AB∥CD，
故本选项能判定AB∥CD；
故选：A．
【点睛】
本题考查了平行线的判定，能灵活运用平行线的判定进行推理是解此题的关键，平行线的判定定理有：①同位角相等，两直线平行，②内错角相等，两直线平行，③同旁内角互补，两直线平行．
6、B
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 内 · · · · · · ○ · · · · · ·
号学级年名姓
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 外 · · · · · · ○ · · · · · ·
【分析】
根据三角形外角的性质可直接进行求解．
【详解】
解：∵，，
∴；
故选B．
【点睛】
本题主要考查三角形外角的性质，熟练掌握三角形外角的性质是解题的关键．
7、C
【分析】
连接，，根据圆周角定理可得，根据切线性质以及四边形内角和性质，求解即可．
【详解】
解：连接，，如下图：
∴
∵PA、PB是的切线，A、B是切点
∴
∴由四边形的内角和可得：
故选C．
【点睛】
此题考查了圆周角定理，切线的性质以及四边形内角和的性质，解题的关键是熟练掌握相关基本性质．
8、B
【分析】
直接根据圆周角定理求解．
【详解】
解：，
．
故选：B．
【点睛】
本题考查了圆周角定理，解题的关键是掌握在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．
9、D
【分析】
分别根据单独一个数也是单项式、多项式中每个单项式的最高次数是这个多项式的次数、单项式中的数字因数是这个单项式的系数、单项式中所有字母的指数和是这个单项式的次数解答即可．
【详解】
解：A、0是单项式，正确，不符合题意；
B、多项式的次数是4，正确，不符合题意；
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 内 · · · · · · ○ · · · · · ·
号学级年名姓
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 外 · · · · · · ○ · · · · · ·
C、的系数是，正确，不符合题意；
D、的系数是－1，次数是1，错误，符合题意，
故选：D．
【点睛】
本题考查单项式、单项式的系数和次数、多项式的次数，理解相关知识的概念是解答的关键．
10、A
【分析】
根据角的表示的性质，对各个选项逐个分析，即可得到答案．
【详解】
A选项中，可用，，三种方法表示同一个角；
B选项中，能用表示，不能用表示；
C选项中，点A、O、B在一条直线上，
∴能用表示，不能用表示；
D选项中，能用表示，不能用表示；
故选：A．
【点睛】
本题考查了角的知识；解题的关键是熟练掌握角的表示的性质，从而完成求解．
二、填空题
1、4
【解析】
【分析】
设被污染的两个数字中左边的数字为x，则右边的数为5-x，然后根据题中所给算法可进行求解．
【详解】
解：设被污染的两个数字中左边的数字为x，则右边的数为5-x，由题意得：
，
，
，
∵d为10的整数倍，且，
∴或110，
∵由图可知校验码为9，
∴当时，则有，解得：，则有右边的数为5-1=4；
当时，则有，解得：，不符合题意，舍去；
∴被污染的两个数字中右边的数字是4；
故答案为4．
【点睛】
本题主要考查一元一次方程的应用，熟练掌握一元一次方程的应用是解题的关键．
2、3
【解析】
【分析】
根据反比例函数的解析式是，设点，根据已知得出，即，求出即可．
【详解】
解：设反比例函数的解析式是，
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 内 · · · · · · ○ · · · · · ·
号学级年名姓
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 外 · · · · · · ○ · · · · · ·
设点是反比例函数图象上一点，
矩形的面积为3，
，
即，
故答案为：3．
【点睛】
本题考查了矩形的面积和反比例函数的有关内容的应用，解题的关键是主要考查学生的理解能力和运用知识点解题的能力．
3、140
【解析】
【分析】
先根据图形得出∠AOB＝40°，再根据和为180度的两个角互为补角即可求解．
【详解】
解：由题意，可得∠AOB＝40°，
则∠AOB的补角的大小为：180°−∠AOB＝140°．
故答案为：140．
【点睛】
本题考查补角的定义：如果两个角的和等于180°（平角），就说这两个角互为补角．即其中一个角是另一个角的补角．熟记定义是解题的关键．
4、-1
【解析】
【分析】
根据有理数减法法则计算即可．
【详解】
解：，
故答案为：-1．
【点睛】
本题考查了有理数减法，解题关键是熟记有理数减法法则，准确计算．
5、15
【解析】
【分析】
通过表格即可求得最高和最低气温，12月3日的温差最大，最大温差为10-（-5）=15℃；
【详解】
解：12月1日的温差：
12月2日的温差：
12月3日的温差：
12月4日的温差：
12月5日的温差：
，
最大温差是15，
故答案为：15．
【点睛】
此题考查了正数与负数以及有理数的减法，熟练掌握运算法则是解本题的关键．
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 内 · · · · · · ○ · · · · · ·
号学级年名姓
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 外 · · · · · · ○ · · · · · ·
三、解答题
1、
（1）见详解；（−2，1）；
（2）8.5；
（3）P（5，3）或（−1，−3）.
【分析】
（1）画出△A1B1C1，据图直接写出C1坐标；
（2）先求出△ABC外接矩形CDEF面积，用之减去三个直角三角形的面积，得△ABC的面积；
（3）先根据P，Q关于x轴对称，得到Q的坐标，再构建方程求解即可．
（1）
解：如图1
△A1B1C1就是求作的与△ABC关于x轴对称的三角形，点C1的坐标（−2，1）；
（2）
解：如图2
由图知矩形CDEF的面积：5×5=25
△ADC的面积：×4×5=10
△ABE的面积：×1×3=
△CBF的面积：×5×2=5
所以△ABC的面积为：25-10--5=8.5．
（3）
解：∵点P(a,a−2)与点Q关于x轴对称，
∴Q(a,2−a)，
∵PQ=6，
∴|(a-2)-(2-a)|=6，解得：a=5或a=-1，
∴P（5，3）或（−1，−3）．
【点睛】
本题考查了作图−轴对称变换，三角形的面积等知识，解题的关键是理解题意，掌握关于坐标轴对称的两点的坐标特征，属于中考常考题型．
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 内 · · · · · · ○ · · · · · ·
号学级年名姓
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 外 · · · · · · ○ · · · · · ·
2、
（1）点E
（2）① 90；② 30或150
（3）N（0，）或（0，- ）
【分析】
（1）AE、BE、AB满足勾股定理，且AE=AB，可知为等腰直角三角形，则∠AEB=45°，故E点可使线段AB的可视角为45°．
（2）①由半径所对的圆周角为90°即可得出∠AMB为90°．
②连接AP、BP，即可得出为等边三角形，由圆周角定理即可求得∠AMB为30°或150°．
（3）以AB为弦作圆M且过点N，由圆周角定理可得出当圆心角AMB最大时，圆周角ANB最大，由直线与圆的位置关系得出当y轴与圆M相切时圆心角AMB最大，进而可求得N点坐标．
（1）
连接AE，BE
∵AE=4，AB=4，AE⊥AB
∴为等腰直角三角形
∴∠AEB=45°．
故使得线段AB的可视角为45°的可视点是点E．
（2）
①有题意可知，此时AB为⊙P直径
由半径所对的圆周角为90°可知∠AMB为90°
②当⊙P的半径为4时，AB为⊙P一条弦，连接AP，BP
∵BP=AP=4，AB=4
∴为等边三角形
∴∠APB=60°
当点M在圆心一侧由圆周角定理知∠AMB=
当点M不在圆心一侧由内切四边形性质可知∠AMB=180°-30°=150°
（3）
（3）解： ∵过不在同一条直线上的三点确定一个圆，
∴A、B、N三点共圆，且过A、B两点的圆有无数个，圆心在直线x=3上.
即：点N的位置为过A、B两点的圆与y轴的交点.
设过A、B两点的圆为⊙M，半径为r.
当r<3时，y轴与⊙M无交点，不符题意舍去.
如图所示：
当r=3时，y轴与⊙M交于一点，此时y轴与⊙M相切，切点即为点N.
当r>3时，y轴与⊙M1交于两点，此时y轴与⊙M1相交，交点设为N1、N2.
连接AM、BM、AN、BN、AM1、BM1、AN1、BN1．
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 内 · · · · · · ○ · · · · · ·
号学级年名姓
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 外 · · · · · · ○ · · · · · ·
此时，∠ANB、∠AMB分别为⊙M中弧AB所对的圆周角和圆心角；
∠AN1B、∠AM1B分别为⊙M1中弧AB所对的圆周角和圆心角.
∵∠1=∠M1AM+∠AM1M，
∠2=∠M1BM+∠BM1M，
∴∠1+∠2=∠M1AM+∠AM1M+∠BM1M+∠M1BM，
即∠AMB=∠M1AM+∠AM1B+∠M1BM
∴∠AMB>∠AM1B
∴∠ANB>∠AN1B
∵∠AN1B=∠AN2B
∴∠ANB>∠AN2B
∴当y轴与⊙M相切于点N时，∠ANB的值最大.
在Rt△AMC中，AM=r=3，AC=2
∴MC=
∵MN⊥y轴，MC⊥AB，
∴四边形OCMN为矩形.
∴ON=MC=
∴N（0，）
同理，当点N在y轴负半轴时，坐标为（0，- ）
综述所述，N（0，）或（0，-）.
【点睛】
本题考查了圆周角定理，将可视角的定义转化为圆内弦AB的圆周角是解题的关键，再结合图象计算即可．
3、
【分析】
根据单项式乘以多项式，多项式乘以多项式的法则进行乘法运算，再合并同类项即可．
【详解】
解：
【点睛】
本题考查的是整式的乘法运算，掌握“单项式乘以多项式与多项式乘以多项式的法则”是解本题的关键．
4、
（1）证明见解析
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 内 · · · · · · ○ · · · · · ·
号学级年名姓
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 外 · · · · · · ○ · · · · · ·
（2）
（3）
【分析】
（1）根据四边形，四边形都是平行四边形，得到和，然后证明，即可证明出；
（2）作于M点，设，首先根据，证明出四边形和四边形都是矩形，然后根据同角的余角相等得到，然后根据同角的三角函数值相等得到，即可表示出BF和FH的长度，进而可求出的值；
（3）过点E作于M点，首先根据题意证明出，得到，，然后根据等腰三角形三线合一的性质得到，设，根据题意表示出，，过点E作，交BD于N，然后由证明出，设，根据相似三角形的性质得出，然后由30°角所对直角边是斜边的一半得到，进而得到，解方程求出，然后表示出，根据勾股定理得到EH和EF的长度，即可求出的值．
（1）
解：∵四边形EFGH是平行四边形
∴
∴
∵四边形ABCD是平行四边形
∴
∴
在和中
∴
∴
∴
∴；
（2）
解：如图所示，作于M点，设
∵四边形和四边形都是平行四边形，
∴四边形和四边形都是矩形
∴
∴
∵
∴，
∴
∴
∴
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 内 · · · · · · ○ · · · · · ·
号学级年名姓
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 外 · · · · · · ○ · · · · · ·
∵
∴
由（1）得：
∴
∴；
（3）
解：如图所示，过点E作于M点
∵四边形ABCD是平行四边形
∴
∵
∴，即
∵
∴
∴
∴
∴
设
∵
∴
∴
∴
由（1）得：
∴
∴
过点E作，交BD于N
∵
∴
∴
∴
设
∴
∴
∵
∴
∵
∴
∴
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 内 · · · · · · ○ · · · · · ·
号学级年名姓
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 外 · · · · · · ○ · · · · · ·
∵
∴
∴
∴
解得：或（舍去）
∴
由勾股定理得：
∴．
【点睛】
此题考查了矩形的性质，相似三角形的性质和判定，勾股定理等知识，解题的关键是熟练掌握矩形的性质，相似三角形的性质和判定，勾股定理，根据题意正确作出辅助线求解．
5、
（1）120°；
（2）见解析；
（3）3．
【分析】
（1）取AD的中点F，连接EF，证明△AEF是等边三角形，进而求得∠B；
（2）作FM⊥BC于M，FN⊥AB于点N，先证明Rt△BFM≌Rt△BFN，再证明Rt△FMG≌Rt△FNA；
（3）连接AG，DF，DG，作FM⊥BC于M，先证明AF=GF=DF，从而得出∠AGH=∠AFD＝30°，进而得出∠DGC=∠DFC=120°，从而得出点G、C、D、F共圆，进而得出CA平分∠BCD，接着可证Rt△FMG≌Rt△FHD，△MCF≌△HCF，进而求得GM=CG=DH=，从而得出BM的值，进而求得BF．
（1）
解：如图1，取AD的中点F，连接EF，
∵DE⊥AC，
∴∠AED=90°，
∴AD=2AF=2EF，
∵AD=2AE，
∴AE=EF=AF，
∴∠CAD=60°，
∵∠B+∠CAD=180°，
∴∠B=120°；
（2）
证明：如图2，作FM⊥BC于M，FN⊥AB于点N，
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 内 · · · · · · ○ · · · · · ·
号学级年名姓
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 外 · · · · · · ○ · · · · · ·
∴∠BMF=∠BNF=90°，∠GMF=∠ANF=90°，
∵BF平分∠ABC，
∴FM=FN，
在Rt△BFM和Rt△BFN中，
，
∴Rt△BFM≌Rt△BFN（HL），
∴BM=BN，
在Rt△FMG和Rt△FNA中，
，
∴Rt△FMG≌Rt△FNA（HL），
∴MG=NA，
∴BN+NA=BM+MG，
∴AB=BG．
（3）
如图3，
连接AG，DF，DG，作FM⊥BC于M，延长GF交AD于N，
∵AF=AD，∠DAE=60°，
∴△ADF是等边三角形，
∴∠AFD=60°，AF=DF，
∵GF=AF，∠DFC=180°-∠AFD=120°，
∴AF=GF=DF，
∴∠FGD=∠FDG，∠FAG=∠FGA，
∴∠AGD=∠AFN+∠DFN=∠AFD=×60°＝30°，
∵∠ADC=120°，AD=DG，
∴∠DGA=∠DAG==30°，
∴∠DGC=180°-∠DGA-∠AGD=180°-30°-30°=120°，
∴∠DGC=∠DFC，
∵∠1=∠2，
∴180°-∠DGC-∠1=180°-∠DFC-∠2，
∴∠GCF=∠FDG，∠DCF=∠FGD，
∴∠GCF=∠DCF，
∵FH⊥CD，
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 内 · · · · · · ○ · · · · · ·
号学级年名姓
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 外 · · · · · · ○ · · · · · ·
∴FM=FH，
∵∠FMG=∠FHD=90°，
∴Rt△FMG≌Rt△FHD（HL），
∴DH=MG，
同理可得：△MCF≌△HCF（HL），
∴CM=CH=2CG，
∴GM=CG=DH，
∴3CG=CD=，
∴GM=CG=，
∴BM=BG-GM=AB-GM=5-=，
在Rt△BFM中，∠BFM=90°-∠FBM=90°-60°=30°，
∴BF=2BM=3．
【点睛】
本题考查了等边三角形的判定和性质，全等三角形的判定和性质，角平分线的性质等知识，解决问题的关键是正确作出辅助线．