陕西省安康市2024届高三下学期第三次质量联考数学（文）试卷(含答案)

这是一份陕西省安康市2024届高三下学期第三次质量联考数学（文）试卷(含答案)，共15页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。


一、选择题
1．设，则( )
A.B.C.D.
2．集合，，则下列选项正确的是( )
A.B.C.D.
3．已知函数，公差不为0的等差数列的前n项和为.若，则( )
A.1012B.2024C.3036D.4048
4．若实数x，y满足约束条件，则的最大值为( )
A.0B.2C.9D.11
5．甲、乙、丙三人被随机的安排在周六、周日值班，每天至少要有一人值班，每人只在其中一天值班.则甲、乙被安排在同一天值班的概率为( )
A.B.C.D.
6．在中，M是AB的中点，，与BN相交于点P，则( )
A.B.C.D.
7．已知正数a，b满足，则( )
A.B.C.D.
8．已知，则( )
A.B.C.D.
9．侧棱长与底面边长均为a的正三棱柱的外接球的表面积为，则( )
A.12B.8C.6D.4
10．已知直线l与椭圆在第四象限交于A、B两点，l与x轴，y轴分别交于C、D两点，若，则l的倾斜角是( )
A.B.C.D.
11．折扇是我国古老文化的延续，在我国已有四千年左右的历史，“扇”与“善”谐音，折扇也寓意“善良“善行”.它常以字画的形式体现我国的传统文化，也是运筹帷幄、决胜千里、大智大勇的象征（如图1）.图2是一个圆台的侧面展开图（扇形的一部分），若两个圆弧DE，AC所在圆的半径分别是6和12，且，则该圆台的体积为( )
A.B.C.D.
12．在平面直角坐标系中，曲线与坐标轴的交点都在圆C上，AB为圆C的直径，点P是直线上任意一点，则的最小值为( )
A.4B.12C.16D.18
二、填空题
13．写出一个对称中心为的奇函数_________.
14．已知数列的前n项和为，且，则_________.
15．直线与抛物线交于A、B两点，若，则_________.
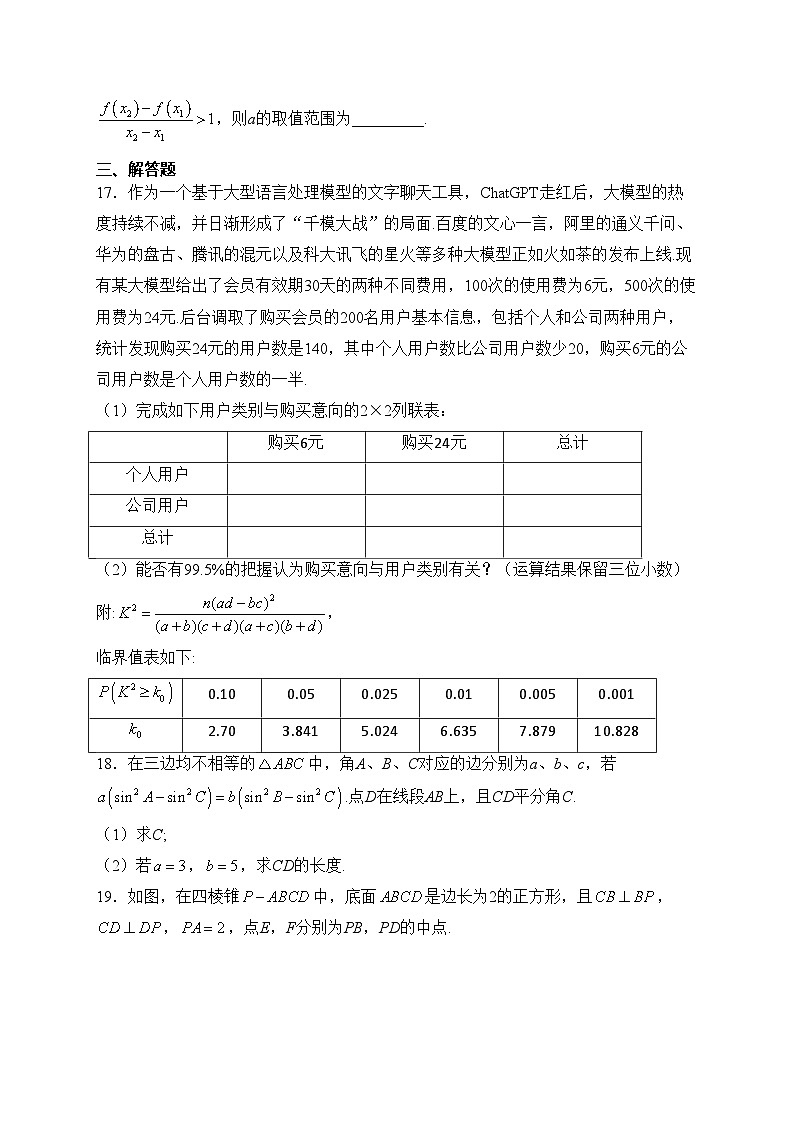
16．已知函数，，，，都有，则a的取值范围为_________.
三、解答题
17．作为一个基于大型语言处理模型的文字聊天工具，ChatGPT走红后，大模型的热度持续不减，并日渐形成了“千模大战”的局面.百度的文心一言，阿里的通义千问、华为的盘古、腾讯的混元以及科大讯飞的星火等多种大模型正如火如茶的发布上线.现有某大模型给出了会员有效期30天的两种不同费用，100次的使用费为6元，500次的使用费为24元.后台调取了购买会员的200名用户基本信息，包括个人和公司两种用户，统计发现购买24元的用户数是140，其中个人用户数比公司用户数少20，购买6元的公司用户数是个人用户数的一半.
（1）完成如下用户类别与购买意向的2×2列联表：
（2）能否有99.5%的把握认为购买意向与用户类别有关？（运算结果保留三位小数）
附:，
临界值表如下:
18．在三边均不相等的中，角A、B、C对应的边分别为a、b、c，若.点D在线段AB上，且CD平分角C.
（1）求C;
（2）若，，求CD的长度.
19．如图，在四棱锥中，底面是边长为2的正方形，且，，，点E，F分别为PB，PD的中点.
（1）求证:平面;
（2）求点P到平面AEF的距离.
20．已知函数的反函数为，令.
（1）求曲线在处的切线的方程;
（2）证明:.
21．已知双曲线的左、右焦点分别为、，两条渐近线的夹角为，是双曲线上一点，且的面积为.
（1）求该双曲线的标准方程;
（2）若直线l与双曲线C交于P、Q两点，且坐标原点O在以PQ为直径的圆上，求的最小值.
22．在直角坐标系中，以坐标原点O为极点，x轴的非负半轴为极轴建立极坐标系，直线l的极坐标方程为，曲线的参数方程为（t为参数），
（1）分别求曲线C和直线l的直角坐标方程;
（2）若直线l交曲线C于A，B两点，过线段AB的中点Q作x轴的平行线交C于一点P，求点P的横坐标.
23．已知函数.
（1）求函数的最小值;
（2）若a，b，c为正实数，且，求的最小值.
参考答案
1．答案：D
解析：由条件可得，所以，即.故选D.
2．答案：A
解析：由条件可得，，所以，，故选A.
3．答案：B
解析：由题可知函数的图象关于直线对称，所以，所以，又，故选B.
4．答案：D
解析：由约束条件，画出可行域，
，化为斜截式方程得，
联立得，即.
由题意可知，当直线过点C时，直线在y轴上的截距最小，此时z最大.
把点代入目标函数可得最大值，即最大值.故选D.
5．答案：C
解析：由题意可知将3人分成两组，其中一组只有1人，另一组有2人.分别安排在周六、周日值班共有6种情况（甲乙，丙）、（甲丙，乙）、（乙丙，甲）、（甲，乙丙）、（乙，甲丙）、（丙，甲乙）.显然甲、乙被安排在同一天有2种情况，所以甲、乙被安排在同一天的概率为.故选C.
6．答案：B
解析：设，由M是AB的中点，得，由，得.
所以，且，
由CM与BN相交于点P可知，点P在线段CM上，也在线段BN上，由三点共线的条件可得，解得，所以，故选B.
7．答案：A
解析：由，解得，所以，，
所以.故选A.
8．答案：A
解析：由，解得，所以，，所以.故选A.
9．答案：C
解析：由球的表面积公式，解得外接球半径.因为底面三角形是边长为a的等边三角形，所以此三角形的外接圆半径为，由正三棱柱的外接球的特点可得，，解得.故选C.
10．答案：C
解析：由可得线段AB的中点，也是线段CD的中点，设，，线段AB的中点坐标为，则，，.又点A，B在椭圆上，所以，两式相减可得，
，所以，所以，即.
又因为A、B、C、D四点共线，所以，综上可得，由A、B在第四象限得即，所以直线的倾斜角为.故选C.
11．答案：D
解析：设圆台上下底面的半径分别为，，由题意可知，解得，，解得，作出圆台的轴截面，如图所示:
图中，，，
过点D向AP作垂线，垂足为T，则，
所以圆台的高，
则上底面面积，，由圆台的体积计算公式可得:
.
故选: D.
12．答案：B
解析：曲线与坐标轴的交点分别为，，，设圆心，由得，所以圆C方程为，其圆心，半径为，圆心到直线的距离设为d，则，所以最小值为4，则最小值为.故选B.
13．答案：
解析：因为奇函数关于原点对称，且此函数又关于点对称，所以此函数可类比于正弦函数，因为正弦函数是奇函数，且关于点对称，所以可联想到.
14．答案：-4
解析：当时，，解得.
当时，，，两式相减得，
因为，所以，所以，所以数列是首项为-2，公比为-1的等比数列，所以，即数列是-2，2，-2，2，……，故，，所以.
15．答案：
解析：由，联立得，所以，且，，显然直线过抛物线的焦点.所以，解得.
16．答案：
解析：由，，，不妨设，则，所以，
可变形化简为，
构造函数，则，
所以在上是单调递增函数，
所以恒成立，
即在上恒成立，
当时，，，
又时，，而，所以，所以，
所以a的取值范围为.
故答案为:.
17．答案：（1）见解析
（2）有的把握认为用户类别与购买意向有关系
解析：（1）设购买24元的个人用户数为x，则购买24元的公司用户数为，设购买6元的公司用户数为y，则购买6元的个人用户数为，则有，解得，，所以用户类别与购买意向列联表如下:
（2）由（1）中列联表得，
所以有的把握认为用户类别与购买意向有关系.
18．答案：（1）
（2）
解析：（1）由，得，
化简得，
因为三边均不相等，所以，即，
由余弦定理得，
在中，由，得.
（2）在中，，故，
由得，易得.
在中，，，所以，
在中，由，得.
19．答案：（1）证明见解析
（2）
解析：（1）证明：因为底面为正方形，所以，
又因为，，，平面，
所以平面，
因为平面，所以，
同理，又因为，，平面，所以平面.
（2）显然由（1）可得，在直角中，，同理，，点E，F分别为PB，PD的中点，所以在中，，
所以，
在直角中，，
由（1）得平面ABP，所以平面ABP，所以点F到平面APE的距离为设点P到平面AEF的距离为h，由，
得，解得.所以点P到平面AEF的距离为.
20．答案：（1）
（2）证明见解析
解析：（1）函数的反函数为，
则，，所以，，
所以曲线在处的切线的方程为，即.
（2）证明：由（1）可知，显然为上的增函数.
因为，，所以存在唯一的，使.
从而有，.
因为时，，时，，
所以在区间上单调递减，在区间上单调递增.
所以，
当且仅当时，等号成立，而，即.
21．答案：（1）
（2）
解析：（1）由题可知双曲线的渐近线方程为，
因为，所以，所以直线的斜率大于1.
由两条渐近线的夹角为可得，因为，所以，
即双曲线方程为，因为的面积为，
所以，所以.
因为点在双曲线上，所以将点的坐标代入方程可得，
解得或.因为条件，所以，即双曲线的方程为.
（2）因为以PQ为直径的圆过坐标原点，所以，所以，即:.
①当直线l的斜率不存在时，设直线l的方程为，设，，
由可得，
又点P、Q在双曲线上，代入可得，解得，.
所以.
②当直线l的斜率存在时，设直线l的方程为，由联立消去y整理得，因为直线l与双曲线交于P，Q两点，所以，且判别式.设，，则，
由得到:，所以，即，
所以，
化简得.
所以.
当时上式取等号，且方程有解.
综上可得的最小值是.
22．答案：（1）；
（2）
解析：（1）由可得，代入，
,消去参数t，可得C的直角坐标方程为:，
化简可得，所以.
将，代入l的极坐标方程，可得l的直角坐标方程为:.
（2）曲线是抛物线，其焦点，准线，
直线，恰好过抛物线的焦点.
由并整理得，
设，，
则，线段AB的中点Q的横坐标，中点Q的纵坐标，
过点Q作x轴的平行线交C于一点P，则点P的纵坐标也等于，所以点P的横坐标为.
23．答案：（1）时，函数取得最小值
（2）9
解析：（1），
在上单调递减，在上单调递增，
所以，即当时，函数取得最小值.
（2）由（1）可得当x为正实数时，，
则由可得:，
所以
，
当且仅当，，时，
又，即当，，时，等号成立.
所以的最小值为9.
购买6元
购买24元
总计
个人用户
公司用户
总计
0.10
0.05
0.025
0.01
0.005
0.001
2.70
3.841
5.024
6.635
7.879
10.828
购买6元
购买24元
总计
个人用户
40
60
100
公司用户
20
80
100
总计
60
140
200