最新中考数学压轴大题之经典模型 专题24 函数与菱形存在性问题-【压轴必刷】

这是一份最新中考数学压轴大题之经典模型 专题24 函数与菱形存在性问题-【压轴必刷】，文件包含专题24函数与菱形存在性问题-压轴必刷2023年中考数学压轴大题之经典模型培优案原卷版docx、专题24函数与菱形存在性问题-压轴必刷2023年中考数学压轴大题之经典模型培优案解析版docx等2份试卷配套教学资源，其中试卷共98页， 欢迎下载使用。

今天整理了初三中考总复习阶段在教学过程中收集的经典题目，一共有31讲，包括原卷版和解析版，供大家学习复习参考。
经典题目1：这是一道非常经典的最值问题，最值模型将军饮马和一箭穿心。
经典题目2：上面三道题是费马点经典问题，旋转转化是费马点问题的关键。
经典题目3：阿氏圆经典题目，这道题目实际包括了隐圆模型，一箭穿心模型等常见几何模型。
经典题目4：这是中考出现频率比较高的胡不归问题，也是经典最值问题。
【压轴必刷】2023年中考数学压轴大题之经典模型培优案
专题24函数与菱形存在性问题
解题策略
我们已经知道菱形是特殊的平行四边形，它的判定方法一共有五种，分别是
①四边都相等的四边形是菱形；②两条对角线互相垂直的平行四边形是菱形 ；③邻边相等的平行四边形是菱形；④对角线互相垂直平分的四边形是菱形 ；⑤一条对角线平分一个顶角的平行四边形是菱形.
在做几何证明题的时候我们常用的判定方法主要是前三种.
二次函数和菱形存在性问题作为压轴题目，结合了“分类讨论思想”，“方程思想”“菱形的判定方法”，势必要比单纯的菱形判定思考难度要大的多，纵观历年中考真题，菱形存在性问题主要是以“两定两动”为设问方式，其中两定指的是四边形四个顶点其中有两个顶点的坐标是确定的或者是可求解的；两动指的是其中一个动点在一条直线或者抛物线上，另外一个动点是平面内任意一点或者该动点也在一条直线或者抛物线上.
经典例题
【例1】（2022春•锡山区校级期中）如图，在矩形ABCD中，BD是对角线，AB＝6cm，BC＝8cm，点E从点D出发，沿DA方向匀速运动，速度是2cm/s；点F从点B出发，沿BD方向匀速运动，速度是1cm/s，MN是过点F的直线，分别交AB、BC于点M、N，且在运动过程中始终保持MN⊥BD．连接EM、EN、EF，两点同时出发，设运动时间为t（s）（0＜t＜3.6），请回答下列问题：
（1）求当t为何值时，△EFD∽△ABD？
（2）求当t为何值时，△EFD为等腰三角形；
（3）将△EMN沿直线MN进行翻折，形成的四边形能否是菱形？若存在，求出t的值；若不存在，请说明理由．
【分析】（1）当△ABD∽△EFD时，则，代入计算即可；
（2）分ED＝EF，DE＝DF，FE＝FD三种情形，分别画出图形，利用相似相似三角形的判定与性质可得答案；
（3）当EM＝EN时，过点E作EK⊥BC于K，利用勾股定理分别表示出EM和EN的长，从而得出方程解决问题．
【解答】解：（1）由题意得：DE＝2tcm，BF＝tcm＜
∵四边形ABCD是矩形，
∴∠BAD＝90°，
在Rt△ABD中，BD＝＝＝10cm，
∴DF＝BD＝BF＝（10﹣t）cm，
当△ABD∽△EFD时，
则，
即，
解得t＝，
即当t为时，△EFD∽△ABD；
（2）①当ED＝EF时，过点E作EG⊥BF于G，
∵ED＝EF，
∴△EFD为等腰三角形，
又∴EG⊥DF，
∴DG＝DF＝（10﹣t）cm，
∵∠EDG＝∠BDA，∠EGD＝∠BAD＝90°，
∴△EGD∽△BAD，
∴，
即＝，
∴t＝；
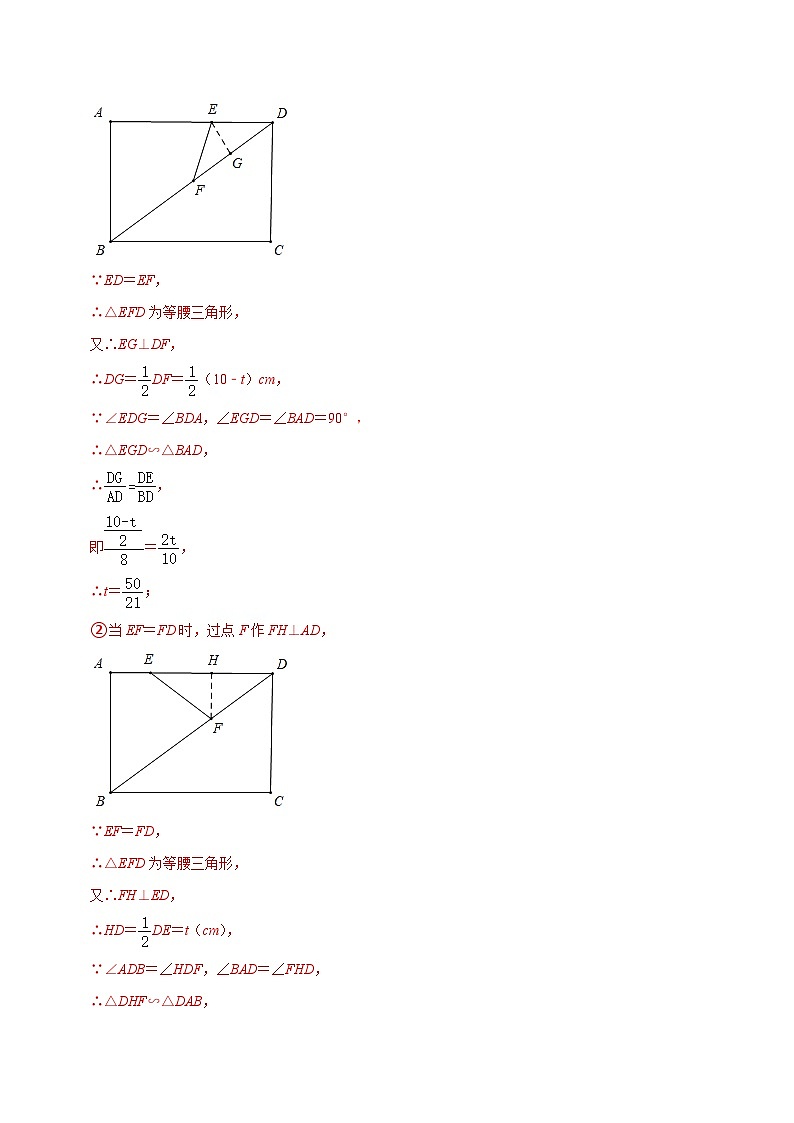
②当EF＝FD时，过点F作FH⊥AD，
∵EF＝FD，
∴△EFD为等腰三角形，
又∴FH⊥ED，
∴HD＝DE＝t（cm），
∵∠ADB＝∠HDF，∠BAD＝∠FHD，
∴△DHF∽△DAB，
即，
∴t＝＞3.6（舍去），
当DE＝DF时，即2t＝10﹣t，
解得：t＝，
综上，当t＝或时，△EFD为等腰三角形；
（4）假设存在符合题意的t，则EM＝EN，
过点E作EK⊥BC于K，
则四边形EKCD为矩形，
∴ED＝CK＝2t（cm），EK＝CD＝6cm，NK＝BC﹣BN﹣CK＝8﹣t﹣2t＝（8﹣t）cm，
∴EN2＝EK2+NK2＝+100，EM2＝AM2+AE2＝t2﹣52t+100，
∴+100＝t2﹣52t+100，
解得t1＝t2＝0，
∵t≠0，不合题意，
∴不存在四边形是菱形．
【例2】（2022秋•南岸区校级期中）如图，点A、B分别在x轴和y轴的正半轴上，以线段AB为边在第一象限作等边△ABC，S△ABC＝，且CA⊥x轴．
（1）若点C在反比例函数y＝（k≠0）的图象上，求该反比例函数的解析式；
（2）在（1）中的反比例函数图象上是否存在点N，使四边形ABCN是菱形，若存在请求出点N坐标，若不存在，请说明理由；
（3）在（2）的条件下，取OB的中点M，将线段OM沿着y轴上下移动，线段OM的对应线段是O1M1，直接写出四边形CM1O1N周长的最小值．
【分析】（1）如图1中，作CD⊥y轴于D．首先证明四边形OACD是矩形，利用反比例函数k的几何意义解决问题即可；
（2）如图2中，作BD⊥AC于D，交反比例函数图象于N，连接CN，AN，求出D的坐标，证明四边形ABCN是菱形即可；
（3）过点C作y轴的对称点C′，将点C′向下平移0.5个单位得到点C″，连接C″N交y轴于点O1，在O1上方0.5个单位处取点M1，则四边形CM1O1N周长的最小，进而求解．
【解答】解：（1）如图1中，作CD⊥y轴于D．
∵CA∥y轴，CD⊥y轴，
∴CD∥OA，AC∥OD，
∴四边形OACD是平行四边形，
∵∠AOD＝90°，
∴四边形OACD是矩形，
∴k＝S矩形OACD＝2S△ABC＝2，
∴反比例函数的解析式为y＝；
（2）存在，理由：
如图2中，作BD⊥AC于D，交反比例函数图象于N，连接CN，AN．
∵△ABC是等边三角形，面积为，设CD＝AD＝m，则BD＝m，
∴×2m×m＝，
∴m＝1或﹣1（舍弃），
∴B（0，1），C（，2），A（，0），
∴N（2，1），
∴BD＝DN，
∵AC⊥BN，
∴CB＝CN，AB＝AN，
∵AB＝BC，
∴AB＝BC＝CN＝AN，
∴四边形ABCN是菱形，
∴N（2，1）；
（3）由点M是OB的中点知，OM＝0.5＝O1M1，
由点C、N的坐标得，CN＝＝2，
如图3，过点C作y轴的对称点C′（﹣，2），将点C′向下平移0.5个单位得到点C″（﹣，），连接C″N交y轴于点O1，在O1上方0.5个单位处取点M1，连接C′M1、CM1，此时，四边形CM1O1N周长的最小．
理由：由C′C″＝O1M1且C′C″∥O1M1知，四边形C′C″O1M1为平行四边形，则C′M1＝C″O1，而由图象的对称性知，C′M1＝CM1，
则四边形CM1O1N周长＝CN+CM1+O1M1+O1N＝2+0.5+O1N+CM1＝2.5+C′M1+O1N＝2.5+C″O1+O1N＝2.5+C″N为最小，
即四边形CM1O1N周长最小值＝2.5+C″N＝2.5+＝．
【例3】（2022秋•龙华区期中）已知：在平面直角坐标系中，直线l1：y＝﹣x+2与x轴，y轴分别交于A、B两点，直线l2经过点A，与y轴交于点C（0，﹣4）．
（1）求直线l2的解析式；
（2）如图1，点P为直线l1一个动点，若△PAC的面积为10时，请求出点P的坐标．
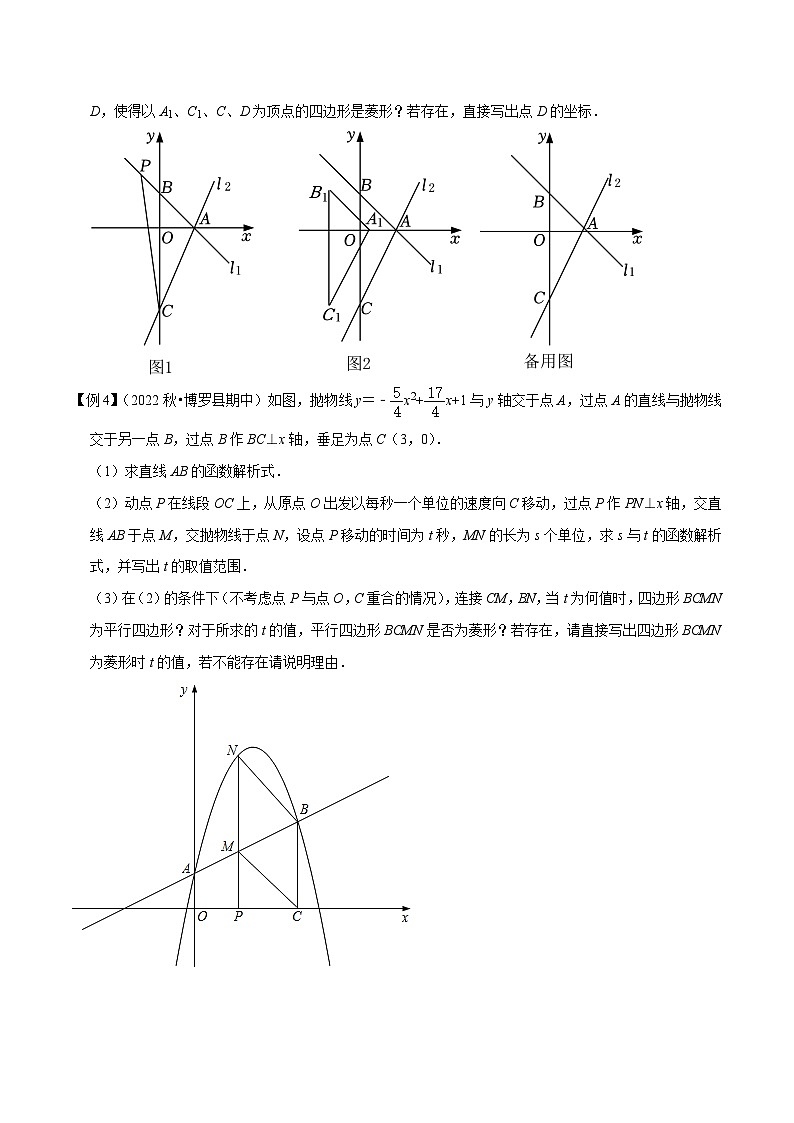
（3）如图2，将△ABC沿着x轴平移，平移过程中的△ABC记为△A1B1C1，请问在平面内是否存在点D，使得以A1、C1、C、D为顶点的四边形是菱形？若存在，直接写出点D的坐标．
【分析】（1）求出A点坐标，再用待定系数法求函数的解析式即可；
（2）设P（t，﹣t+2），分两种情况讨论：当P点在B点左侧时，S△PAC＝S△ABC+S△BCP＝6+×6×（﹣t）＝10，可求P（﹣，）；当P点在A点右侧时，S△PAC＝×6×（t﹣2）＝10，可求P或（，﹣）；
（3）设△ABC向左平移m个单位长，D（x，y），则A1（2﹣m，0），C1（﹣m，﹣4），根据菱形的对角线情况可分三种情况讨论：当CD为菱形对角线时，，求得D（﹣5，0）；当AC1为菱形对角线时，，求得D（2，0）；当A1D为菱形对角线时，，求得D（﹣2，﹣8）．
【解答】解：（1）令x＝0，则y＝2，
∴B（0，2），
令y＝0，则x＝2，
∴A（2，0），
设直线AC的解析式为y＝kx+b，
∴，
解得，
∴直线l2的解析式为y＝2x﹣4；
（2）∵B（0，2），A（2，0），
∴OA＝OB，
∴∠ABO＝45°，
∵C（0，﹣4），
∴OC＝4，
∴BC＝6，OA＝2，
∴S△ABC＝×6×2＝6，
∴P点在B点左侧或在A点右侧，
设P（t，﹣t+2），
当P点在B点左侧时，
∴S△PAC＝S△ABC+S△BCP＝6+×6×（﹣t）＝10，
解得t＝﹣，
∴P（﹣，）；
当P点在A点右侧时，
∴S△PAC＝S△PBC﹣S△ABC＝×（t﹣2）×6＝10，
解得t＝
∴P（，﹣）；
综上所述：P点坐标为（﹣，）或（，﹣）；
（3）存在点D，使得以A1、C1、C、D为顶点的四边形是菱形，理由如下：
设△ABC向左平移m个单位长，D（x，y），
∴A1（2﹣m，0），C1（﹣m，﹣4），
当CD为菱形对角线时，
，
解得，
∴D（﹣5，0）；
当AC1为菱形对角线时，
，
解得或（舍），
∴D（2，0）；
当A1D为菱形对角线时，
，
解得（舍）或，
∴D（﹣2，﹣8）；
综上所述：D点坐标为（﹣5，0）或（2，0）或（﹣2，﹣8）．
【例4】（2022秋•博罗县期中）如图，抛物线y＝﹣x2+x+1与y轴交于点A，过点A的直线与抛物线交于另一点B，过点B作BC⊥x轴，垂足为点C（3，0）．
（1）求直线AB的函数解析式．
（2）动点P在线段OC上，从原点O出发以每秒一个单位的速度向C移动，过点P作PN⊥x轴，交直线AB于点M，交抛物线于点N，设点P移动的时间为t秒，MN的长为s个单位，求s与t的函数解析式，并写出t的取值范围．
（3）在（2）的条件下（不考虑点P与点O，C重合的情况），连接CM，BN，当t为何值时，四边形BCMN为平行四边形？对于所求的t的值，平行四边形BCMN是否为菱形？若存在，请直接写出四边形BCMN为菱形时t的值，若不能存在请说明理由．
【分析】（1）把x＝0代入y＝﹣x2+x+1，求出y的值，得到A点坐标，把x＝3代入y＝﹣x2+x+1，求出y的值，得到B点坐标，设直线AB的解析式为y＝kx+b，将A、B两点的坐标代入，利用待定系数法即可求出直线AB的解析式为y＝x+1；
（2）根据路程＝速度×时间得出OP＝1•t＝t，那么P（t，0）（0≤t≤3），再求出M、N的坐标，利用s＝MN＝NP﹣MP即可求出s与t的函数关系式；
（3）由于BC∥MN，所以当BC＝MN时，四边形BCMN为平行四边形，根据MN＝BC列出方程﹣t2+t＝，解方程求出t的值，得出t＝1或2时，四边形BCMN为平行四边形；根据有一组邻边相等的平行四边形是菱形，分t＝1、t＝2两种情况，计算MN与MC，比较大小，如果相等，则四边形BCMN是菱形；如果不相等，则四边形BCMN不是菱形．
【解答】解：（1）∵当x＝0时，y＝1，
∴A（0，1）．
当x＝3时，y＝﹣×32+×3+1＝2.5，
∴B（3，2.5），
设直线AB的解析式为y＝kx+b，
则：，解得：，
∴直线AB的解析式为y＝x+1；
（2）∵动点P在线段OC上从原点出发以每秒一个单位的速度向C移动，点P移动的时间为t秒，
∴OP＝1•t＝t，
∴P（t，0）（0≤t≤3），
∵过点P作PN⊥x轴，交直线AB于点M，交抛物线于点N，
∴M（t，t+1），N（t，﹣t2+t+1），
∴s＝MN＝NP﹣MP＝﹣t2+t+1﹣（t+1）＝﹣t2+t（0≤t≤3）；
（3）由题意，可知当MN＝BC时，四边形BCMN为平行四边形，
此时，有﹣t2+t＝，
解得t1＝1，t2＝2，
所以当t＝1或2时，四边形BCMN为平行四边形．
①当t＝1时，MP＝，NP＝4，故MN＝NP﹣MP＝，
又在Rt△MPC中，MC＝＝，故MN＝MC，此时四边形BCMN为菱形；
②当t＝2时，MP＝2，NP＝，故MN＝NP﹣MP＝，
又在Rt△MPC中，MC＝＝，故MN≠MC，此时四边形BCMN不是菱形．
综上，当t＝1或2时，四边形BCMN为平行四边形．当t＝1时，四边形BCMN为菱形．
培优训练
一．解答题
1．（2022秋•思明区校级期中）如图，正方形OABC的边OA、OC分别在x轴和y轴上，顶点B在第一象限，AB＝6，点E、F分别在边AB和射线OB上运动（E、F不与正方形的顶点重合），OF＝2BE，设BE＝t．
（1）当t＝2时，则AE＝ 4 ，BF＝ 2 ；
（2）当点F在线段OB上运动时，若△BEF的面积为，求t的值；
（3）在整个运动过程中，平面上是否存在一点P，使得以P、O、E、F为顶点，且以OF为边的四边形是菱形？若存在，求出t的值；若不存在，请说明理由．
【分析】（1）由题意可直接得出答案；
（2）由题意易得，进而得到FH＝6﹣2t，然后求解即可；
（3）根据题意易得OF、EF、EO的长，要使以P，O，E，F为顶点的四边形是菱形，故而有三种情况：一是OF＝EF，二是OE＝EF，三是OE＝OF，然后分别求解即可．
【解答】解：（1）∵AB＝6，BE＝2，
∴AE＝AB﹣BE＝6﹣2＝4，
∵AO＝AB，∠A＝90°，
∴，
∴，
∴；
故答案为：4，2；
（2）如图，作FH⊥AB于H，
由题意，得，
∴FH＝6﹣2t，
∵＝，
∴，
解得：；
（3）由已知得：，EF2＝（6﹣2t）2+（6﹣3t）2＝13t2﹣60t+72，OE2＝（6﹣t）2+62＝t2﹣12t+72，
若OF＝EF，如图，
∴8t2＝13t2﹣60t+72，
解得：，
若OE＝EF，如图，
∴t2﹣12t+72＝13t2﹣60t+72，
解得：t＝4，
若OE＝OF，如图，
∴t2﹣12t+72＝8t2，
解得：．
综上所述，或t＝4或．
2．（2022•城西区开学）如图，在平面直角坐标系中，直线y＝2x+4与x轴，y轴分别交于A，B两点，直线y＝﹣x+1与x轴，y轴分别交于C，D两点，这两条直线相交于点P．
（1）求点P的坐标；
（2）求四边形AODP的面积；
（3）在坐标平面内是否存在一点Q，使以A，P，D，Q为顶点的四边形是菱形？若存在，请求出点Q的坐标，若不存在，请说明理由．
【分析】（1）联立两一次函数解析式即可求出交点坐标；
（2）根据四边形AODP的面积＝S△ACP﹣S△OCD求解即可；
（3）由A（﹣2，0），P（﹣1，2）求出AP＝＝，由C（1，0），D（0，1），P（﹣1，2）求出AD＝＝，DP＝＝，可得AD＝AP，则以A，P，D，Q为顶点的四边形是菱形时，只能以PD为对角线，根据菱形的性质即可求解．
【解答】解：（1）联立直线y＝2x+4与直线y＝﹣x+1得：，
∴，
∴点P的坐标为（﹣1，2）；
（2）由直线y＝2x+4得A（﹣2，0），B（0，4），
由直线y＝﹣x+1得C（1，0），D（0，1），
∴AC＝3，OC＝1，OD＝1，
∴S△ACP＝×3×2＝3，
S△OCD＝×1×1＝，
∴四边形AODP的面积＝S△ACP﹣S△OCD＝3﹣＝；
（3）∵A（﹣2，0），P（﹣1，2），
∴AP＝＝，
∵C（1，0），D（0，1），P（﹣1，2），
∴AD＝＝，DP＝＝，
∴AD＝AP，
∴以A，P，D，Q为顶点的四边形是菱形时，只能以PD为对角线，
如图：
∴存在，点Q的坐标为（1，3）．
3．（2022春•大足区期末）已知：在平面直角坐标系中，直线l1：y＝﹣x+2与x轴，y轴分别交于A、B两点，直线l2经过点A，与y轴交于点C（0，﹣4）．
（1）求直线l2的解析式；
（2）如图1，点P为直线l1一个动点，若△PAC的面积等于10时，请求出点P的坐标；
（3）如图2，将△ABC沿着x轴平移，平移过程中的△ABC记为△A1B1C1，请问在平面内是否存在点D，使得以A1、C1、C、D为顶点的四边形是菱形？若存在，直接写出点D的坐标．
【分析】（1）设直线l2的解析式y＝kx+b，求出点A的坐标，把A、C的坐标代入解析式计算即可；
（2）设点P的横坐标为t，根据三角形的面积公式建立方程，求解即可．
（3）按CC1为菱形边长和对角线两种情况讨论，最后根据菱形的性质求出点D的坐标即可．
【解答】解：（1）设直线l2的解析式y＝kx+b，
∵直线l1：y＝﹣x+2与x轴，y轴分别交于A、B两点，
∴A（2，0），B（0，2），
∵直线l2经过点A，与y轴交于点C（0，﹣4），
∴，
∴，
∴直线l2的解析式：y＝2x﹣4；
（2）由题意可知，BC＝6，
设点P的横坐标为m，
∴S△PAC＝•|xA﹣xP|•BC＝|2﹣m|×6＝10，
∴m＝﹣或m＝．
∴P（﹣，）或P（，）．
（3）设将△ABC沿着x轴平移t个单位长度得到△A1B1C1，
∴A1（2﹣t，0），
∴CC1＝t，A1C1＝AC＝2，
设D点坐标为（p，q），
①当CC1为以A1、C1、C、D为顶点的菱形边长时，有两种情况：
当CC1＝A1C1＝2时，即t＝2，
此时CC1∥A1D，即点D在x轴上，
且A1D＝A1C1＝2，
∴点D与点A重合，即D（2，0）．
当CC1＝A1C＝t时，
∵A1（2﹣t，0），C（0，﹣4），
∴（﹣4）2+（2﹣t）2＝t2，
解得t＝5，
此时CC1∥A1D，即点D在x轴上，
且A1D＝CC1＝5，
∴D（﹣8，0）．
②当CC1为以A1、C1、C、D为顶点的菱形对角线时，A1C1＝A1C＝2，即点A1在CC1的垂直平分线上，且A1，D关于CC1对称，
当△ABC向左一移动，A1（2﹣t，0），C（0，﹣4），C1（﹣t，﹣4），
∴（﹣4）2+（2﹣t）2＝（2）2，
解得t＝4或t＝0（舍），
当△ABC向右移动时，A1（2+t，0），C（0，﹣4），C1（t，﹣4），
∴（﹣4）2+（2+t）2＝（2）2，
解得t＝﹣4（舍）或t＝0（舍），
∴A1（﹣2，0），
∴D（﹣2，﹣8）．
综上所述，存在点D，使得以A1、C1、C、D为顶点的四边形是菱形，点D的坐标为（2，0），（﹣8，0），（﹣2，﹣8）．
4．（2022•崆峒区校级二模）如图，抛物线y＝﹣x2+bx+c交y轴于点A（0，2），交x轴于点B（4，0）、C两点，点D为线段OB上的一个动点（不与O、B重合），过点D作DM⊥x轴，交AB于点M，交抛物线于点N．
（1）求抛物线的解析式；
（2）连接AN和BN，当△ABN的面积最大时，求出点D的坐标及△ABN的最大面积；
（3）在平面内是否存在一点P，使得以点A，M，N，P为顶点，以AM为边的四边形是菱形？若存在，请求出点P的坐标；若不存在，请说明理由．
【分析】（1）将A，B的坐标代入抛物线的解析式组成二元一次方程组，求解即可；
（2）设D（t，0）（0＜t＜4），根据坐标的特点，可得出点M，N的坐标，再根据三角形的面积公式可表达△ABN的面积，根据二次函数的性质可得出结论；
（3）根据题意，易证△AEM∽△AOB，由此得出AE和AM的长，再根据题意需要分两种情况讨论：①当AM＝MN时，②当AM＝AN时，分别求解即可．
【解答】解：（1）将点A（0，2），点B（4，0）代入抛物线y＝﹣x2+bx+c，
∴，
∴．
∴抛物线的解析式为：y＝﹣x2+x+2．
（2）∵点A（0，2），点B（4，0），
∴直线AB的解析式为：y＝﹣x+2；
设D（t，0）（0＜t＜4），
∵DM⊥x轴，点M在直线AB上，点N在抛物线上，
∴M（t，﹣t+2），N（t，﹣t2+t+2），
∴MN＝﹣t2+t+2﹣（﹣t+2）＝﹣t2+4t，
∴△ABN的面积＝•MN•（xB﹣xA）＝•（﹣t2+4t）•4＝﹣2（t﹣2）2+8，
∵﹣2＜0，0＜t＜4，
∴当t＝2时，△ABN有最大值，最大值为8，此时D（2，0）．
（3）存在，如图，过点M作ME⊥y轴于点E，
∴ME∥OB，ME＝1，
∴∠AEM＝∠AOB＝90°，∠AME＝∠ABO，
∴△AEM∽△AOB，
∴AE：AO＝AM：AB＝ME：OB，
Rt△AOB中，OA＝2，OB＝4，
∴AB＝2，
∴＝＝，
∴AE＝t，AM＝t．
根据题意，需要分两种情况讨论：
①AM＝MN时，如图，
此时t＝﹣t2+4t（0＜t＜4），
解得t＝或t＝0（舍），
∴AM＝，
∴AP＝AM＝，
∵AP∥MN，
∴点P在y轴上，
∴OP＝2+＝，
∴P（0，）；
②当AM＝AN时，如图，此时AP与MN互相垂直平分，设MN与AP交于点F，
∴MF＝MN＝（﹣t2+4t），
∵MF＝AE＝t，
∴（﹣t2+4t）＝t，
解得t＝3或t＝0（舍），
∴AP＝2t＝6，
∴P（6，2）．
综上，存在点P，使得以点A，M，N，P为顶点，以AM为边的四边形是菱形，此时P（0，）或（6，2）．
5．（2022•前进区三模）如图，在平面直角坐标系中，矩形ABCO的边OC与x轴重合，OA与y轴重合，BC＝2，D是OC上一点，且OD，DC的长是一元二次方程x2﹣5x+4＝0的两个根（OD＞DC）．
（1）求线段OD，OC，AD的长；
（2）在线段AB上有一动点P（不与A、B重合），点P从点A出发，以每秒1个单位长度的速度沿AB方向匀速运动，到终点B停止，设运动的时间为t秒，过P点作PE∥BD交AD于E，PF∥AD交BD于F，求四边形DEPF的面积S与时间t的函数关系式；
（3）在（2）的条件下，在点P运动的过程中，x轴上是否存在点Q，使以A、D、P、Q为顶点的四边形是菱形？若存在，请直接写出点Q的坐标，若不存在，请说明理由．
【分析】（1）解方程可得OD＝4，CD＝1，即可求解；
（2）先证明四边形PEDF是矩形，由锐角三角函数可求PE，PF的长，即可求解；
（3）分两种情况讨论，由勾股定理可求解．
【解答】解：（1）∵OD，DC的长是一元二次方程x2﹣5x+4＝0的两个根（OD＞DC）．
∴OD＝4，CD＝1，
∴OC＝5，AD＝＝＝2；
（2）∵PE∥BD，PF∥AD，
∴四边形PEDF是平行四边形，
∵BD＝＝＝，
∴BD2+AD2＝5+20＝25，
∵AB2＝25，
∴BD2+AD2＝AB2，
∴∠ADB＝90°，
∴四边形PEDF是矩形，
∵sin∠BAC＝，
∴，
∴PE＝t，
∵PF∥AD，
∴∠BPF＝∠BAD，
∴cs∠BPF＝cs∠BAD＝，
∴＝，
∴PF＝（5﹣t），
∴S＝PE•PF＝t×（5﹣t），
∴S＝﹣t2+2t；
（3）存在点Q，使以A、D、P、Q为顶点的四边形是菱形，
设P（t，2），
∴PD2＝（4﹣t）2+22，
当PD，AP为边，
∵四边形APDQ是菱形，
∴PD＝AP，
则t2＝（4﹣t）2+22，解得：t＝，
∴AP＝，
∴DQ＝AP＝，
∴点Q（，0）；
当AD，AP为边，∵四边形APQD是菱形，
∴PD＝AP，
∴2＝t，
∴AP＝2，
∴DQ＝AP＝2，
∴DQ＝AP＝2，
∴点Q（4+2，0），
综上所述：点Q（4+2，0）或（，0）．
6．（2021秋•莱西市期末）已知：如图，菱形ABCD中，AB＝5cm，AC＝6cm，动点P从点B出发，沿BA方向匀速运动；同时，动点Q从点C出发，沿CB方向匀速运动，它们的运动速度均为1cm/s．过点P作PM∥BC，过点B作BM⊥PM，垂足为M，连接QP．设运动时间为t（s）（0＜t＜5）．解答下列问题：
（1）菱形ABCD的高为 cm，cs∠ABC的值为 ；
（2）在运动过程中，是否存在某一时刻t，使四边形MPQB为平行四边形？若存在，求出t的值；若不存在，请说明理由．
（3）是否存在某一时刻t，使四边形MPQB的面积是菱形ABCD面积的？若存在，求出t的值；若不存在，请说明理由．
（4）是否存在某一时刻t，使点M在∠PQB的角平分线上？若存在，求出t的值；若不存在，请说明理由．
【分析】（1）连接BD交AC于点O，作AE⊥BC于点E，根据菱形的性质得BC＝AB＝5cm，OA＝OC＝3cm，∠AOB＝90°，根据勾股定理求得OB＝4cm，即可求得菱形ABCD的面积为24cm2，由5AE＝24得AE＝，即菱形ABCD的高为；再由勾股定理求得BE＝cm，则BE：AE：AB＝7：24：25，所以cs∠ABC＝；
（2）由四边形MPQB为平行四边形，且∠M＝90°得四边形MPQB是矩形，所以∠PQB＝90°，可推导出BQ＝BP，可列方程5﹣t＝t，求出t的值即可；
（3）由＝cs∠BPM＝cs∠ABC＝，＝sin∠BPM＝sin∠ABC＝得PM＝t，BM＝t，再根据S四边形MPQB＝S菱形ABCD列方程×t（t+5﹣t）＝×24，解方程求出符合题意的t值即可；
（4）作MR⊥QP交直线QP于点R，先由＝tan∠BPM＝tan∠ABC＝得MP＝MB，可知MP＜MB，而MR≤MP，所以MR＜MB，这说明点M到∠PQB的两边的距离不相等，所以不存在某一时刻t，使点M在∠PQB的角平分线上．
【解答】解：（1）如图1，连接BD交AC于点O，作AE⊥BC于点E，则∠AEB＝90°，
∵四边形ABCD是菱形，AB＝5cm，AC＝6cm，
∴BC＝AB＝5cm，BD⊥AC，OA＝OC＝AC＝3cm，
∴∠AOB＝90°，
∴OD＝OB＝＝＝4（cm），
∴S菱形ABCD＝AC•OD+AC•OB＝×6×4+×6×4＝24（cm2），
∴5AE＝24，
∴AE＝（cm），
∴菱形ABCD的高为cm；
∵BE＝＝＝（cm），
∴BE：AE：AB＝7：24：25，
∴cs∠ABC＝＝，
∴cs∠ABC的值为，
故答案为：，．
（2）存在，
如图2，∵四边形MPQB为平行四边形，且∠M＝90°，
∴四边形MPQB是矩形，
∴∠PQB＝90°，
∴＝cs∠ABC＝，
∴BQ＝BP，
∵BP＝CQ＝t，
∴BQ＝5﹣t，
∴5﹣t＝t，
解得t＝，
∴t的值为．
（3）存在，
如图1，∵PM∥BC，
∴∠BPM＝∠ABC，
∴＝cs∠BPM＝cs∠ABC＝，＝sin∠BPM＝sin∠ABC＝，
∴PM＝t，BM＝t，
∵S四边形MPQB＝S菱形ABCD，
∴×t（t+5﹣t）＝×24，
整理得18t2﹣125t+100＝0，
解得t1＝，t2＝（不符合题意，舍去）．
∴t的值为.
（4）不存在，
理由：如图3，作MR⊥QP交直线QP于点R，
∵∠MBQ＝180°﹣∠PMB＝90°，
∴MB⊥QB，
∵＝tan∠BPM＝tan∠ABC＝，
∴MP＝MB，
∴MP＜MB，
∵MR≤MP，
∴MR＜MB，
∴点M不可能在∠PQB的平分线上，
∴不存在某一时刻t，使点M在∠PQB的角平分线上．
7．（2022•青岛一模）已知，在菱形ABCD中，对角线AC，BD相交于点O，AC＝6cm，BD＝8cm．延长BC至点E，使CE＝BC，连接ED．点F从点E出发，沿ED方向向点D运动，速度为1cm/s，过点F作FG⊥ED垂足为点F交CE于点G；点H从点A出发，沿AD方向向点D运动，速度为1cm/s，过点H作HP∥AB，交BD于点P，当F点停止运动时，点H也停止运动．设运动时间为t（0＜t≤3），解答下列问题：
（1）求证：∠BDE＝90°；
（2）是否存在某一时刻t，使G点在ED的垂直平分线上？若存在，求出t值；若不存在，请说明理由．
（3）设六边形PCGFDH的面积为S（cm2），求S与t的函数关系式；
（4）连接HG，是否存在某一时刻t，使HG∥AC？若存在，求出t值；若不存在，请说明理由．
【分析】（1）证明CD＝CB，CE，可得结论；
（2）存在．由题意CD＝CE，点G在DE的垂直平分线上，推出EF＝DF＝3cm，由此可得结论；
（3）根据S六边形HPCGFD＝S△DPH+S△BDE﹣S△CBP﹣S△EFG，求解即可；
（4）当AC∥HG时，AH＝CG，构建方程求解．
【解答】（1）证明：∵四边形ABCD是平行四边形，
∴BC＝CD，
∵CD＝CE，
∴CD＝CB＝CE，
∴∠BDE＝90°；
（2）解：存在．
理由：∵四边形ABCD是菱形，
∴AD∥CE，AD＝BC，
∵CE＝BC，
∴AD＝CE，
∴四边形ADEC是平行四边形，
∴AC＝DE＝6cm，
∵CD＝CE，点G在DE的垂直平分线上，
∴EF＝DF＝3cm，
∴t＝3；
（3）解：过点H作HJ⊥BD于点J．
∵四边形ABCD是菱形，
∴AC⊥BD，OA＝OC＝3cm，OB＝OD＝4cm，
∴AB＝AD＝＝＝5cm，
∵PH∥AB，
∴＝，
∴＝，
∴DP＝（5﹣t）cm，
∵HJ∥AO，
∴＝，
＝，
∴HJ＝（5﹣t）cm，
∴S△DPH＝•PD•HJ＝×（5﹣t）×（5﹣t）＝（5﹣t）2，
∴S六边形HPCGFD＝S△DPH+S△BDE﹣S△CBP﹣S△EFG
＝（5﹣t）2+×6×8﹣×[8﹣（5﹣t）]×3﹣×t×t
＝﹣t2﹣t+36；
（4）存在．
理由：当AC∥HG时．AH＝CG，
∴t＝5﹣t，
∴t＝．
8．（2021秋•市南区期末）已知：如图，菱形ABCD中，对角线AC，BD相交于点O，且AC＝6cm，BD＝8cm．点P从点B出发，沿BA方向匀速运动，速度为1cm/s；同时，直线EF从点D出发，沿DB方向匀速运动，速度为1cm/s，EF⊥BD，且与AD，BD，CD分别交于点E，Q，F．当直线EF停止运动，点P也停止运动．连接PF，设运动时间为t（s）．解答下列问题：
（1）用含t的代数式表示线段EF： cm ；
（2）当t为何值时，四边形ADFP是平行四边形；
（3）设四边形APFE的面积为y（cm2），求y与t之间的函数关系式；
（4）是否存在某一时刻t，使得PF与EF的夹角为45°？若存在，求出t的值，若不存在，说明理由．
【分析】（1）证明△DEF∽△DAC，进而求得结果；
（2）证明并根据△DQF∽△DOC表示出DF，根据DF＝AP求得结果；
（3）根据S四边形APFE＝﹣S梯形APFD﹣S△DEF，分别计算出梯形ADFP和三角形DEF的面积，进而求得结果；
（4）设PF与BD交于点H，作PG⊥BD于G，依次表示出PG，BG，QF，HQ，BH＝BD﹣DQ﹣HQ，根据H＝BG+GH列出方程求得结果．
【解答】解：（1）∵四边形ABCD是菱形，
∴AC⊥BD，OD＝，OC＝，
∵EF⊥BD，
∴EF∥AC，
∴△DEF∽△DAC，
∴，
∴，
∴EF＝．
故答案是： cm；
（2）在Rt△COD中，OC＝3，OD＝4，
∴CD＝5，
∵EF∥AC，
∴△DQF∽△DOC，
∴，
∴，
∴DF＝，
∵AP∥DF，
∴当AP＝DF时，四边形ADFP是平行四边形，
∴5﹣t＝，
∴t＝；
（3）如图1，
作CG⊥AB于G，
∵得，
5•CG＝6×8，
∴CG＝，
∵S梯形APFD＝＝＝12，
＝＝，
∴S四边形APFE＝﹣S梯形APFD﹣S△DEF＝﹣++12，
∴y＝﹣++12；
（4）如图2，
假设存在t，使∠PFE＝45°，设PF与BD交于点H，作PG⊥BD于G，
∴PG＝BP•sinABD＝t•＝，BG＝BP•cs∠ABD＝t＝，
QF＝DQ•tan∠CDB＝t＝，
∵∠PQH＝90°，∠PFE＝45°，
∴∠FHQ＝45°，
∴HQ＝QF＝，
∴BH＝BD﹣DQ﹣HQ＝8﹣t﹣＝8﹣，
∵∠PGH＝90°，∠PHG＝∠FHQ＝45°，
∴PG＝GH＝，
由BH＝BG+GH得，
8﹣＝+，
∴t＝，
∴当t＝时，PF与EF的夹角为45°．
9．（2022春•双峰县期末）问题情境：在综合实践课上，老师让同学们探究“平面直角坐标系中的旋转问题”，如图，在平面直角坐标系中，四边形AOBC是矩形，O（0，0），点A（5，0），点B（0，3）．
操作发现：以点A为中心，顺时针旋转矩形AOBC，得到矩形ADEF，点O，B，C的对应点分别为D，E，F．
（1）如图1，当点D落在BC边上时，求点D的坐标；
继续探究：（2）如图2，当点D落在线段BE上时，AD与BC交于点H，求证△ADB≌△AOB；
拓展探究：如图3，点M是x轴上任意一点，点N是平面内任意一点，是否存在点N使以A、D、M、N为顶点的四边形是菱形？若存在，请直接写出点N的坐标；若不存在，请说明理由．
【分析】（1）根据点A、B的坐标可得OA、OB的长度，再利用勾股定理可得CD的长，从而得出点D的坐标；
（2）利用HL证明Rt△ADB≌Rt△AOB即可；
拓展探究：分AD＝AM，DA＝DM，MD＝MA三种情形，分别画出图形，根据菱形的性质解决问题．
【解答】（1）解：∵点A（5，0），点B（0，3）．
∴OA＝5，OB＝3，
∵四边形AOBC是矩形，
∴AC＝OB＝3，OA＝BC＝5，∠OBC＝∠C＝90°，
∵顺时针旋转矩形AOBC，得到矩形ADEF，
∴AD＝AO＝5，
在Rt△ADC中，CD＝＝4，
∴BD＝BC﹣CD＝1，
∴D（1，3）；
（2）证明：∵四边形ADEF是矩形，
∴∠ADE＝90°，
∵点D在线段BE上，
∴∠ADB＝90°，
由（1）可知：AD＝AO，
又∵AB＝AB，∠AOB＝90°，
∴Rt△ADB≌Rt△AOB（HL），
拓展探究：存在，
由（1）得：D（1，3），
∴AD＝＝5，
当AD＝AM时，如图，
则ND＝AD＝5，ND∥OA，
∴N（﹣4，3）或（6，3），
当MD＝AD时，点D与N关于x轴对称，
∴N（1，﹣3），
当MD＝MA时，如图，四边形ANDM为菱形，
∴DN∥AM，DN＝AM＝DM，
设HM＝a，则DM＝AM＝4﹣a，
∴32+a2＝（4﹣a）2，
解得a＝，
∴DN＝4﹣＝，
∴N（），
综上所述，存在点N使以A、D、M、N为顶点的四边形是菱形，N的坐标为：（﹣4，3）或（6，3）或（1，﹣3）或（）．
10．（2022春•营口期末）如图1，直线y＝x+6与x，y轴分别交于A，B两点，∠ABO的角平分线与x轴相交于点C．
（1）求点C的坐标；
（2）在直线BC上有两点M，N，△AMN是等腰直角三角形，∠MAN＝90°，求点M的坐标；
（3）点P在y轴上，在平面上是否存在点Q，使以点A、B、P、Q为顶点的四边形为菱形？若存在，请直接写出点Q的坐标；若不存在，请说明理由．
【分析】（1）先求出点A和点B的坐标，利用勾股定理求出AB的长度，设OC＝t，过点C作CH⊥AB于H，根据角平分线的性质得CH＝OC＝t，由S△ABO＝S△ABC+S△BCO得到t的值，即可得到点C的坐标；
（2）求出直线BC的表达式为：y＝2x+6，设点M（m，2m+6）、N（n，2n+6），过点M作MF⊥x轴于点F，过点N作NE⊥x轴于点E，证明△FMA≌△EAN（AAS），则EN＝AF，MF＝AE，即可求解；
（3）分AB是边、AB是对角线两种情况，根据菱形的性质分别求解即可．
【解答】解：（1）对于直线y＝x+6，令x＝0，得到y＝6，
∴B（0，6），
令y＝0，得到x＝﹣8，
∴A（﹣8，0）．
∵A（﹣8，0），B（0，6），
∴OA＝8，OB＝6，
∵∠AOB＝90°，
∴AB＝＝10，
过点C作CH⊥AB于H，设OC＝t，
∵BC平分∠ABO，∠AOB＝90°，
∴CH＝OC＝t，
∵S△ABO＝S△ABC+S△BCO，
∴OA•OB＝AB•CH+OC•OB，
∴6×8＝10t+6t，
∴t＝3，
∴OC＝3，
∴C（﹣3，0）；
（2）设线BC的表达式为：y＝kx+b，
∵B（0，6），C（﹣3，0），
∴直线BC的表达式为：y＝2x+6，
设点M（m，2m+6）、N（n，2n+6），
过点M作MF⊥x轴于点F，过点N作NE⊥x轴于点E，
∵△AMN为等腰直角三角形，故AM＝AN，
∵∠NAE+∠MAF＝90°，∠MAF+∠AMF＝90°，
∴∠NAE＝∠AMF，
∵∠AFM＝∠NEA＝90°，AM＝AN，
∴△FMA≌△EAN（AAS），
∴EN＝AF，MF＝AE，
即﹣2n﹣6＝m+8，2m+6＝8+n，
解得：m＝﹣2，n＝﹣6，
故点M的坐标为（﹣2，2）、点N（﹣6，﹣6）；
由于M，N的位置可能互换，故点N的坐标为（﹣2，2）、点M（﹣6，﹣6）；
综上所述，点M的坐标为（﹣2，2）或（﹣6，﹣6）；
（3）设点P（0，p），
∴BP2＝（p﹣6）2，AP2＝82+p2，
①当AB是边时，如图，
∵点A、B、P、Q为顶点的四边形为菱形，
∴BP＝AB＝10，BP′＝AB＝10，OB＝OP″，
∵B（0，6），
∴P（0，16），P′（0，﹣4），P″（0，﹣6），
∵A（﹣8，0），
∴Q（﹣8，10），Q′（﹣8，﹣10），Q″（8，0）；
②当AB是对角线时，如图，
∵点A、B、P、Q为顶点的四边形为菱形，
∴AP＝BP，
∴BP2＝AP2，
∴（p﹣6）2＝82+p2，解得p＝﹣，
∴P（0，﹣），
∵A（﹣8，0），B（0，6），
∴Q（﹣8，）；
综上所述，点Q的坐标为（﹣8，10）或（﹣8，﹣10）或（8，0）或（﹣8，）．
11．（2022春•曹妃甸区期末）如图，在矩形ABCD中，AB＝3，∠CAB＝30°，点P从点A出发，每秒个单位长度的速度沿AB方向运动，点Q从点C出发，以每秒2个单位长度的速度沿对角线CA方向运动．已知点P、Q两点同时出发．当点Q到达点A时，P、Q两点同时停止运动，连接PQ，设运动时间为t秒．
（1）BC＝ 3 ，AC＝ 6 ；
（2）当t为何值时，AP＝AQ；
（3）在运动过程中，是否存在一个时刻t，使所得△APQ沿它的一边翻折，翻折前后两个三角形组成的四边形为菱形？若存在，求出t的值；若不存在，请说明理由．
（4）当点P关于点Q的对称点P′落在△ACD的内部（不包括边上）时，请直接写出t的取值范围．
【分析】（1）根据矩形的性质和含30°角的直角三角形的性质解答即可；
（2）根据直角三角形的性质和三角形的面积公式解答即可；
（3）分三种情况，利用翻折的性质解答即可；
（4）根据对称的性质解答即可．
【解答】解：（1）∵矩形ABCD，AB＝3，∠CAB＝30°，
∴BC＝3，AC＝6；
故答案为：3；6；
（2）由题意知，AP＝t，AQ＝6﹣2t，
∵AQ＝AP，
∴6﹣2t＝t，
∴t＝12﹣6；
（3）解：①当沿PQ翻折时，则AP＝AQ，则t＝6﹣2t，
解得：t＝12﹣6，
②当沿AP翻折时，则AQ＝QP，过点Q作QM⊥AB，垂足为M，
则AM＝AP＝t，
在Rt△AQM中，∠QAM＝30°，
∴t＝（6﹣2t），
解得：t＝2，
③当沿AQ翻折时，则AP＝PQ，
过点P作PM⊥AC，垂足为M，
则AM＝AQ＝3﹣t，
在Rt△AMP中，∠PAM＝30°，
∴3﹣t＝×t，
解得：t＝，
综上所述，t的值为12﹣6或2或；
（4）由题意知，AP＝t，AQ＝6﹣2t，
∴P'在△ACD内部，满足，
∴1.5＜t＜2．
12．（2022春•巴东县期末）已知点E是平行四边形ABCD边CD上的一点（不与点C，D重合）．
（1）如图1，当点E运动到CD的中点时，连接AE、BE，若AE平分∠BAD，证明：CE＝CB．
（2）如图2，过点E作EF⊥DC交直线CB于点F，连接AF．若∠ABC＝120°，BC＝2．封AB＝4．在线段CF上是否存在一点H．使得四边形AFHD为菱形？若存在，请求出ED，CH的长；若不存在，请简单地说明理由．
【分析】（1）先根据平行四边形的性质证得∠DEA＝∠BAE，再根据角平分线的性质证得∠DAE＝∠DEA，得出AD＝DE，根据E是CD的中点得出AE＝CE，进而得出CE＝CB，结论得证．
（2）当DH⊥CF且CE＝1+时，四边形AFHD为菱形，先根据一组对边平行且相等的四边形是平行四边形证明四边形AFHD是平行四边形，再证明AD＝DH证得平行四边形AFHD是菱形．
【解答】（1）证明：∵四边形ABCD是平行四边形，
∴AB∥CD，AD＝BC，
∴∠DEA＝∠BAE，
又∵AE平分∠BAD，
∴∠DAE＝∠BAE，
∴∠DAE＝∠DEA，
∴AD＝DE，
又∵E是CD的中点，
∴DE＝CE，
∴CE＝CB；
（2）解：存在，当DH⊥CF且CE＝1+时，四边形AFHD为菱形，
理由如下：过点D作DH⊥CF于H，如图所示：
∵四边形ABCD是平行四边形
∴AB＝CD＝4，AD＝BC＝2，∠ABC＝∠ADC＝120°，
∴∠BAD＝∠BCD＝60°，
∵CE＝1+，
∴DE＝CD﹣CE＝4﹣（1﹣）＝3﹣，
在Rt△CHD中，∠CHD＝90°，∠DCH＝60°，
∴∠CDH＝30°，
∴CH＝CD＝2，
∴DH＝，
∴AD＝DH，
在Rt△CEF中，∠CEF＝90°，∠ECF＝60°，
∴∠CFE＝30°，
∴CF＝2CE＝2（1+）＝2+2，
∴FH＝CF﹣CH＝2+2﹣2＝2
∴AD＝FH，
在平行四边形ABCD中，AD∥BC，点F在CB的延长线上，
∴AD∥FH，
∴四边形AFHD是平行四边形，
又∵AD＝DH，
∴平行四边形AFHD是菱形．
13．（2022春•同江市期末）如图，平面直角坐标系中，把矩形OABC沿对角线OB所在的直线折叠，点A落在点D处，OD与BC交于点E．OA，OC的长满足式子|OA﹣6|+＝0．
（1）求点A，C的坐标；
（2）直接写出点E的坐标，并求出直线AE的函数解析式；
（3）F是x轴上一点，在坐标平面内是否存在点P，使以O，B，P，F为顶点的四边形为菱形？若存在，请直接写出点P的坐标；若不存在，请说明理由．
【分析】（1）根据非负数的性质求出OA、OC的长，即可解决问题；
（2）首先证明EO＝EB，设EO＝EB＝x，在Rt△ECO中，EO2＝OC2+CE2，构建方程求出x，可得点E坐标，再利用待定系数法即可解决问题；
（3）分两种情形分别求解即可解决问题．
【解答】解：（1）由|OA﹣6|+＝0．
可得OA＝6，OC＝3，
∴A（6，0），C（0，3）；
（2）∵OA∥BC，
∴∠CBO＝∠AOB，
根据翻折不变性可知：∠EOB＝∠AOB，
∴∠EOB＝∠EBO，
∴EO＝EB，
设EO＝EB＝x，
在Rt△ECO中，EO2＝OC2+CE2，
∴x2＝32+（6﹣x）2，
解得x＝，
∴CE＝BC﹣EB＝6﹣＝，
∴E（，3），
设直线AE的解析式为y＝kx+b，
∴，
解得，
∴直线AE的函数解析式为y＝﹣x+；
（3）如图，OB＝＝3．
①当OB为菱形的边时，OF1＝OB＝BP1＝3，故P1（6﹣3，3），
OF3＝P3F3＝BP3＝3，故P3（6+3，3）．
②当OB为菱形的对角线时，
∴OP2＝BP2，
∴CP2＝6﹣P2O，
在Rt△OP2C中，P2C2+OC2＝P2O2，
∴（6﹣P2O）2+32＝P2O2，解得P2O＝，
∴CP2＝6﹣＝，
∴P2（，3）），
③当OP4为对角线时，
∵AB⊥x轴，OP4＝OB，
∴P4（6，﹣3），
综上所述，满足条件的点P坐标为（6﹣3，3）或（6+3，3）或（ ，3）或（6，﹣3）．
14．（2022春•抚远市期末）如图，平面直角坐标系中，把矩形OABC沿对角线OB所在的直线折叠，点A落在点D处，OD与BC交于点E．OA，OC的长满足式子|OA﹣6|+＝0．
（1）求点A，C的坐标；
（2）直接写出点E的坐标，并求出直线AE的函数解析式；
（3）F是x轴上一点，在坐标平面内是否存在点P，使以O，B，P，F为顶点的四边形为菱形？若存在，请直接写出点P的坐标；若不存在，请说明理由．
【分析】（1）根据非负数的性质求出OA、OC的长即可解决问题；
（2）首先证明EO＝EB，设EO＝EB＝x，在Rt△ECO中，EO2＝OC2+CE2，构建方程求出x，可得点E坐标，再利用待定系数法即可解决问题；
（3）分三种情形，根据菱形的性质分别求解即可解决问题．
【解答】解：（1）∵OA，OC的长满足式子|OA﹣6|+＝0．
∴OA﹣6＝0，OC2﹣9＝0，
∴OA＝6，OC＝3，
∴A（6，0），C（0，3）；
（2）∵四边形OABC是矩形，
∴OA∥BC，
∴∠CBO＝∠AOB，
根据翻折不变性可知：∠EOB＝∠AOB，
∴∠EOB＝∠EBO，
∴EO＝EB，设EO＝EB＝x，
在Rt△ECO中，EO2＝OC2+CE2，
∴x2＝32+（6﹣x）2，
解得x＝，
∴CE＝BC﹣EB＝6﹣＝，
∴E（，3），
设直线AE的解析式为y＝kx+b，
则有，
解得，
∴直线AE的函数解析式为y＝﹣x+；
（3）如图，
∵OA＝6，OC＝3，
∴OB＝＝3．
①当OB为菱形的边时，OF1＝OB＝BP1＝3，故P1（6﹣3，3），
OF3＝P3F3＝BP3＝3，故P3（6+3，3）．
②当OB为菱形的对角线时，P2O＝P2B，
设P2O＝P2B＝a，则P2C＝6﹣a，
在Rt△P2OC中，P2O2＝OC2+P2C2，
∴a2＝32+（6﹣a）2，
解得a＝，
∴CE＝BC﹣P2B＝6﹣＝，
∴P2（，3），
③当OF4为对角线时，可得P4（6，﹣3），
综上所述，存在，满足条件的点P坐标为（6﹣3，3）或（6+3，3）或（，3）或（6，﹣3）．
15．（2022春•东阳市期末）如图，在平面直角坐标系中，矩形OABC的顶点A、C分别在x轴、y轴上，且B（4，2），E为直线AC上一动点，连OE，过E作GF⊥OE，交直线BC、直线OA于点F、G，连OF．
（1）求直线AC的解析式．
（2）当E为AC中点时，求CF的长．
（3）在点E的运动过程中，坐标平面内是否存在点P，使得以P、O、G、F为顶点的四边形为菱形，若存在，求出点P的横坐标，若不存在，请说明理由．
【分析】（1）设直线AC的解析式：y＝kx+b，将A，C两点坐标代入，进而求得结果；
（2）设CF＝x，可证得△CEF≌△AEG，进而在Rt△COF中，根据勾股定理列出方程，进一步求得结果；
（3）当以OF，OG为边时，根据（2）可求得点F和点G坐标，进而求得点P横坐标；当以OG，FG为边时，延长OF至P，使PF＝OF，在OC的延长线上截取CQ＝OC＝2，连接PQ，
可推出OF平分∠CFG，从而得出OE＝OC＝2，可证得△AOC≌△OQP，进而求得点F点坐标，在Rt△EOG中，根据勾股定理列出方程，进一步可求得F点横坐标；当OF，FG为边时，作FH⊥OG于H，连接CH，作HQ⊥AC与Q，可推出CH平分∠ACO，设OH＝a，在Rt△AHQ中，根据勾股定理可求得a，进而求得点P横坐标．
【解答】解：（1）∵矩形OABC的顶点A、C分别在x轴、y轴上，且B（4，2），
∴点A（4，0），点C（0，2），
设直线AC的解析式：y＝kx+b（k≠0），
代入点A，C坐标，
得，
解得，
∴直线AC解析式：y＝x+2；
（2）∵E为AC的中点，
∴CE＝AE，
在矩形OABC中，BC∥OA，
∴∠FCE＝∠GAE，
又∵∠CEF＝∠AEG，
∴△CEF≌△AEG（ASA），
∴EF＝EG，CF＝AG，
∵OE⊥FG，
∴OE为线段FG的垂直平分线，
∴OF＝OG，
设CF＝x，则AG＝x，
∵A（4，0），
∴OA＝4，
∴OG＝4﹣x，
∴OF＝4﹣x，
在Rt△OCF中，根据勾股定理，
得22+x2＝（4﹣x）2，
解得x＝，
∴CF＝；
（3）存在以P、O、G、F为顶点的四边形为菱形，分情况讨论：
①以OG，OF为边，
则OF＝OG，
∵GF⊥OE，
∴E为FG的中点，
由（2）可知点F（，2），点G（，0），
根据平移的性质，可得点P的坐标为（4，2），
∴点P的横坐标为4；
②如图1，
以OG，FG为边，OG＝FG，
延长OF至P，使PF＝OF，在OC的延长线上截取CQ＝OC＝2，连接PQ，
∴CF＝，CF∥PQ，
∴∠PQO＝∠FCO＝90°，
∵OG＝FG，
∴∠GOF＝∠GFO，
∵BC∥OA，
∴∠CFO＝∠FOG，
∴∠CFO＝∠GFO，
∵∠BCO＝∠OEF，
∴OE＝OC＝2，
同理可得：CF＝EF，
∴OF⊥CE，
∴∠COF+∠ACO＝90°，
∵∠ACO+∠CAO＝90°，
∴∠COF＝∠CAO，
∵∠PQO＝∠AOC＝90°，OQ＝OC＝4，
∴△AOC≌△OQP（ASA），
∴PQ＝OC＝2，
∴CF＝1，
设OG＝FG＝a，
在Rt△EOG中，OE＝OC＝2，EG＝FG﹣EF＝a﹣1，OG＝a，
∴a2﹣（a﹣1）2＝22，
∴a＝，
∴G（，0），F（1，2），
∵1×2﹣＝﹣，
∴P点横坐标为：﹣；
如图2，
以OF，FG为边，OF＝FG，
作FH⊥OG于H，连接CH，作HQ⊥AC与Q，
可得∠OFG＝∠ACO，∠OCH＝∠OFG，
∴CH平分∠ACO，
∴OH＝HQ，CE＝OC＝2，
设OH＝a，
在Rt△AHQ中，HQ＝x，AH＝4﹣x，AQ＝AC﹣CQ＝2﹣2，
∴（4﹣x）2﹣x2＝（2﹣2）2，
∴x＝﹣1，
∴F（﹣1，2），
∴P（﹣1，﹣2），
综上所述：P点横坐标为：4或﹣或﹣1．
16．（2022•大方县模拟）如图，抛物线与x轴交于A，B（4，0）两点，与y轴交于点C，直线经过点B，C，点P是抛物线上的动点，过点P作PQ⊥x轴，垂足为Q，交直线BC于点D．
（1）求抛物线的解析式及点A的坐标；
（2）当点P位于直线BC上方且△PBC面积最大时，求P的坐标；
（3）若点E是平面直角坐标系内的任意一点，是否存在点E，使得以A，C，D，E为顶点的四边形是菱形？若存在，请直接写出所有符合条件的点E的坐标；若不存在，请说明理由．
【分析】（1）把B（4，0）代入，先求出n的值，再求出C的坐标，将点B、C代入解析式，求解即可；
（2）设，则，用含m的代数式表示出DP，可得，利用二次函数求最值求解即可；
（3）分类讨论，当点D在y轴右侧时，当点D在y轴左侧时，有菱形的性质可得CD∥AE，AC＝AE，求出AE的解析式为，设，再根据AC2＝5＝AE2，建立关于t的方程，求解即可．
【解答】解：（1）把B（4，0）代入得﹣2+n＝0，解得n＝2，
∴直线BC的解析式为．
令x＝0，则y＝2，
∴C（0，2）．
把点B（4，0），C（0，2）代入抛物线的解析式，
得，
解得．
∴抛物线的解析式为．
令，解得x1＝﹣1，x2＝4，
∴A（﹣1，0）；
（2）设，则，
∴，
∵B（4，0），
∴OB＝4．
∵＝，
∴当m＝2时，△PBC的面积最大，此时P（2，3）；
（3）存在，理由如下：
当点D在y轴右侧时，∵四边形ACDE为菱形，
∴CD∥AE，AC＝AE，
设AE的解析式为，
把A坐标代入，得，
∴，
∴AE的解析式为，
设，
∵AC2＝5＝AE2，
∴，
解得t＝1或﹣3（舍），
∴E（1，﹣1）；
当点D在y轴左侧时，同理可得，E（﹣3，1）；
综上，E1（1，﹣1），E2（﹣3，1）．
17．（2022•山西模拟）综合与探究
如图，二次函数y＝ax2+bx+4的图象与x轴分别交于点A（﹣2，0），B（4，0），点E是x轴正半轴上的一个动点，过点E作直线PE⊥x轴，交抛物线于点P，交直线BC于点F．
（1）求二次函数的表达式．
（2）当点E在线段OB上运动时（不与点O，B重合），恰有线段PF＝EF，求此时点P的坐标．
（3）试探究：若点Q是y轴上一点，在点E运动过程中，是否存在点Q，使得以点C，F，P，Q为顶点的四边形为菱形，若存在，直接写出点Q的坐标；若不存在，请说明理由．
【分析】（1）将A（﹣2，0），B（4，0）代入y＝ax2+bx+4，即可求函数的解析式；
（2）求出直线BC的解析式，设P（t，﹣t2+t+4），则F（t，﹣t+4），E（t，0），分别求出PF＝﹣t2+2t，EF＝﹣t+4，再由PF＝EF，求出t＝1，即可求P（1，）；
（3）设P（t，﹣t2+t+4），则F（t，﹣t+4），①当P点在F点上方时，当四边形CFPQ1为菱形时，PF＝CQ1，先求Q1（0，﹣t2+2t+4），再由CQ1＝CF，可得Q1（0，4）；当四边形CFPQ2为菱形时，PF＝CQ2，求出Q2（0，t2﹣2t+4），再由Q2F＝CQ2，可得Q2（0，2）；②当P点在F点下方时，PF＝t2﹣2t，由PF＝CQ3，可得Q3（0，﹣t2+2t+4），再由CQ3＝CF，可得Q3（0，﹣4）．
【解答】解：（1）将A（﹣2，0），B（4，0）代入y＝ax2+bx+4，
∴，
解得，
∴y＝﹣x2+x+4；
（2）令x＝0，则y＝4，
∴C（0，4），
设直线BC的解析式为y＝kx+b，
∴，
解得，
∴y＝﹣x+4，
设P（t，﹣t2+t+4），则F（t，﹣t+4），E（t，0），
∴PF＝﹣t2+t+4﹣（﹣t+4）＝﹣t2+2t，EF＝﹣t+4，
∵PF＝EF，
∴﹣t2+2t＝（﹣t+4），
解得t＝1或t＝4，
∵0＜t＜4，
∴t＝1，
∴P（1，）；
（3）存在点Q，使得以点C，F，P，Q为顶点的四边形为菱形，理由如下：
设P（t，﹣t2+t+4），则F（t，﹣t+4），
由（2）知C（0，4），
①当P点在F点上方时，PF＝﹣t2+2t，
当四边形CFPQ1为菱形时，PF＝CQ1，
∴Q1（0，﹣t2+2t+4），
∵CQ1＝CF，
∴﹣t2+2t＝t，
解得t＝0（舍）或t＝4﹣2，
∴Q1（0，4）；
当四边形CFPQ2为菱形时，PF＝CQ2，
∴Q2（0，t2﹣2t+4），
∵Q2F＝CQ2，
∴（﹣t2+2t）2＝t2+（t2﹣t）2，
解得t＝2，
∴Q2（0，2）；
②当P点在F点下方时，
PF＝﹣t+4﹣（﹣t2+t+4）＝t2﹣2t，
∵PF＝CQ3，
∴Q3（0，﹣t2+2t+4），
∵CQ3＝CF，
＝t2﹣2t＝t，
解得t＝0（舍）或t＝4+2，
∴Q3（0，﹣4）；
综上所述：Q点坐标为（0，4）或（0，﹣4）或（0，2）．
18．（2022•建华区二模）综合与实践
如图，已知正方形OCDE中，顶点E（1，0），抛物线y＝x2+bx+c经过点C、点D，与x轴交于A、B两点（点B在点A的右侧），直线x＝t（t＞0）交x轴于点F．
（1）求抛物线的解析式，且直接写出点A、点B的坐标；
（2）若点G是抛物线的对称轴上一动点，且使AG+CG最小，则G点坐标为： （，﹣） ；
（3）在直线x＝t（第一象限部分）上找一点P，使得以点P、点B、点F为顶点的三角形与△OBC全等，请你直接写出点P的坐标；
（4）点M是射线AC上一点，点N为平面上一点，是否存在这样的点M，使得以点O、点A、点M、点N为顶点的四边形为菱形？若存在，请你直接写出点N的坐标；若不存在，请说明理由．
【分析】（1）根据正方形的性质可求得：C（0，﹣1），D（1，﹣1），再运用待定系数法即可求得答案；
（2）连接AD交抛物线的对称轴于点G，连接CG，如图，则此时AG+CG最小，运用待定系数法求得直线AD的解析式为y＝﹣x﹣，即可求得点G的坐标；
（3）分两种情形：①△OBC≌△FBP或②△OBC≌△FPB，分别建立方程求解即可；
（4）利用待定系数法可得直线AC的解析式为y＝﹣x﹣1，设M（m，﹣m﹣1）（m＞﹣1），分三种情况：①当OM、AN为对角线时，如图1，②当AM、ON为对角线时，如图2，③当OA、MN为对角线时，如图3，分别画出图形，根据菱形性质建立方程求解即可得出答案．
【解答】解：（1）∵E（1，0），
∴OE＝1，
∵四边形OCDE是正方形，
∴OC＝CD＝CE＝OE＝1，∠CDE＝∠DEO＝∠OCD＝90°，
∴C（0，﹣1），D（1，﹣1），
∵抛物线y＝x2+bx+c经过点C（0，﹣1），点D（1，﹣1），
∴，
解得：，
∴抛物线解析式为：y＝x2﹣x﹣1，
∵抛物线y＝x2+bx+c与x轴交于A、B两点（点B在点A的右侧），
∴令y＝0，即有x2﹣x﹣1＝0，
整理得：（x+1）（x﹣2）＝0，．
解得：x1＝﹣1，x2＝2，
∴A点坐标为（﹣1，0），B点坐标为（2，0）；
（2）G点坐标为：（，﹣），理由如下：
∵抛物线y＝x2﹣x﹣1经过C（0，﹣1），D（1，﹣1），
∴C、D关于抛物线的对称轴：直线x＝对称，
连接AD交抛物线的对称轴于点G，连接CG，如图，
则此时AG+CG最小，
∵C、D关于抛物线的对称轴：直线x＝对称，
∴CG＝DG，
∴AG+CG＝AG+DG＝AD（两点之间，线段最短）
∵A（﹣1，0），D（1，﹣1），
∴直线AD的解析式为y＝﹣x﹣，
∵连接AD交抛物线的对称轴：直线x＝于点G，
∴当x＝时，y＝﹣×﹣＝﹣，
∴G（，﹣）；
故答案为：（，﹣）；
（3）符合条件的点P的坐标为（4，1）或（3，2），理由如下：
∵由（1）知C（0，﹣1），B（2，0），x轴⊥y轴（即OC⊥AB），
∴OC＝1，OB＝2，∠BOC＝90°，
∴BC＝，
∵在直线x＝t（第一象限部分）上找一点P，使得以点P、点B、点F为顶点的三角形与△OBC全等，
∴OF＝t，PF⊥x轴
∴BF＝OF﹣OB＝t﹣2，
分三种情形：①△OBC≌△FBP或②△OBC≌△FPB或③△OBC≌△BPF，
∴FP＝OC＝1，BF＝OB＝2，t＞2或FP＝OB＝2，BF＝OC＝1，t＞2或FP＝OB＝2，BF＝OC＝1，0＜t＜2，
∴t﹣2＝2或t﹣2＝1或2﹣t＝1，
∴t＝4或t＝3或t＝1，
∴P（4，1）或（3，2）或（1，2）；
（4）存在符合条件的点M和N，点N坐标为（﹣1，﹣1）或（﹣，）或（，﹣），理由如下：
设直线AC的解析式为y＝kx+d，把A（﹣1，0），C（0，﹣1）代入，
得：，
解得：，
∴直线AC的解析式为y＝﹣x﹣1，
∵点M是射线AC上一点，点N为平面上一点，
∴设M（m，﹣m﹣1）（m＞﹣1），
①当OM、AN为对角线时，如图1，
∵四边形OAMN是菱形，
∴AM＝MN＝OA＝1，MN∥OA，
∴（m+1）2+（﹣m﹣1）2＝1，
解得：m＝﹣1+或m＝﹣1﹣（不符合题意，舍去），
∴M（﹣1+，﹣），
∴N（，﹣）；
②当AM、ON为对角线时，如图2，
∵四边形OAMN是菱形，
∴AN＝MN＝OA＝OM＝1，MN∥OA，AN∥OM，
∴m2+（﹣m﹣1）2＝1，
解得：m＝0或m＝﹣1（不符合题意，舍去），
∴M（0，﹣1），
∴N（﹣1，﹣1）；
③当OA、MN为对角线时，如图3，
∵四边形OAMN是菱形，
∴MN⊥OA，AM＝OM，MN与OA互相垂直平分，即M与N关于x轴对称，
∴（m+1）2+（﹣m﹣1）2＝m2+（﹣m﹣1）2，
解得：m＝﹣，
∴M（﹣，﹣），
∴N（﹣，）；
综上所述，点N的坐标为（，﹣）或（﹣1，﹣1）或（﹣，）．
19．（2022•红花岗区模拟）如图，在平面直角坐标系中，抛物线y＝ax2+bx+4与x轴交于A（﹣1，0），B（4，0）两点，与y轴交于点C．
（1）求抛物线的解析式；
（2）点P在抛物线上，当∠PBA＝∠ACO时，求点P的坐标；
（3）将抛物线的对称轴沿x轴向右平移个单位得直线l，点M为直线l上一动点，在平面直角坐标系中是否存在点N，使以点B，C，M，N为顶点的四边形为菱形？若存在，请求出点N的坐标；若不存在，请说明理由．
【分析】（1）运用待定系数法直接求出抛物线解析式即可；
（2）得出tan∠PBA＝tan∠ACO＝＝，求出OE＝1，得出点E的坐标，求出直线BE的解析式，联立直线BE和抛物线方程，则可得出点P的坐标；
（3）由题意得直线l：x＝2，设出点M的坐标，分两种情况求出点M的坐标，根据菱形的性质即可得出结论．
【解答】解：（1）∵抛物线y＝ax2+bx+4与x轴交于A（﹣1，0），B（4，0）两点，
∴，
解得，．
∴抛物线的解析式为y＝﹣x2+3x+4；
（2）如图，设直线PB与OC交于点E，
∵抛物线解析式y＝﹣x2+3x+4与y轴交于点C，
∴C（0，4），
又∵A（﹣1，0），
∴OA＝1，OC＝4，
∴tan∠ACO＝＝，
∵∠PBA＝∠ACO，
∴tan∠PBA＝tan∠ACO＝＝，
∴OE＝1，
∴E（0，1）或（0，﹣1），设直线BE的解析式为y＝mx+n，
∴或，
解得或，
∴直线BE的解析式为y＝﹣x+1或y＝x﹣1，
∴或，
解得，x1＝﹣，x2＝4（舍去），x3＝﹣，x4＝4（舍去），
∴P（﹣，）或（﹣，﹣）；
（3）由（1）知，抛物线解析式为y＝﹣x2+3x+4，对称轴直线为x＝，
∴将抛物线的对称轴沿x轴向右平移个单位得直线l：x＝2，
设M（2，m），
∵B（4，0），C（0，4），
∴BC2＝OB2+OC2＝32，
CM2＝22+（m﹣4）2＝m2﹣8m+20，
BM2＝m2+（4﹣2）2＝m2+4，
①当CN为对角线时，如图，
∵以点B，C，M，N为顶点的四边形为菱形，
∴CM＝CB，
∴CM2＝CB2，
∴m2﹣8m+20＝32，
∴m＝4+2或4﹣2，
∴M（2，4+2）或（2，4﹣2），
∵B（4，0），C（0，4），
∴N（6，2）或（6，﹣2）；
②当BN为对角线时，如图，
∵以点B，C，M，N为顶点的四边形为菱形，
∴BM＝CB，
∴BM2＝CB2，
∴m2+4＝32，
∴m＝2或﹣2，
∴M（2，2）或（2，﹣2），
∵B（4，0），C（0，4），
∴N（﹣2，4+2）或（﹣2，4﹣2）；
综上所述，存在点N，使以点B，C，M，N为顶点的四边形为菱形，点N的坐标为（6，2）或（6，﹣2）或（﹣2，4+2）或（﹣2，4﹣2）．
20．（2022•蒲城县一模）如图，已知直线与x轴、y轴分别交于B、C两点，抛物线y＝ax2+3x+c经过B、C两点，与x轴的另一个交点为A，点E的坐标为．
（1）求抛物线的函数表达式；
（2）点E，F关于抛物线的对称轴直线l对称，Q点是对称轴上一动点，在抛物线上是否存在点P，使得以E、F、P、Q为顶点的四边形是菱形？若存在，求出点P的坐标；若不存在，请说明理由．
【分析】（1）由，可得B（3，0），C（0，），用待定系数法得抛物线的函数表达式是y＝﹣x2+3x+；
（2）y＝﹣x2+3x+＝﹣（x﹣1）2+6，得抛物线的对称轴是直线x＝1，关键E（0，），F关于抛物线的对称轴直线x＝1对称，得F（2，），设Q（1，t），P（m，﹣m2+3m+），分3种情况：①当EF，PQ是对角线时，EF的中点即是PQ的中点，，得m＝1，又EQ＝FQ，故P（1，6）；②当EQ，FP为对角线时，EQ，FP的中点重合，，得P（﹣1，0），Q（1，0），又FQ＝2＝PQ，故P（﹣1，0）；③当EP，FQ为对角线，EP，FQ的中点重合，，可得P（3，0）．
【解答】解：（1）在中，令x＝0得y＝，令y＝0得x＝3，
∴B（3，0），C（0，），
把B（3，0），C（0，）代入y＝ax2+3x+c得：
，
解得，
∴抛物线的函数表达式是y＝﹣x2+3x+；
（2）在抛物线上存在点P，使得以E、F、P、Q为顶点的四边形是菱形，理由如下：
∵y＝﹣x2+3x+＝﹣（x﹣1）2+6，
∴抛物线的对称轴是直线x＝1，
∵E（0，），F关于抛物线的对称轴直线x＝1对称，
∴F（2，），
设Q（1，t），P（m，﹣m2+3m+），
①当EF，PQ是对角线时，EF的中点即是PQ的中点，如图：
∴，
解得m＝1，
∵E（0，），F关于抛物线的对称轴直线x＝1对称，
∴EQ＝FQ，
∴以E、F、P、Q为顶点的四边形是菱形，
∴P（1，6）；
②当EQ，FP为对角线时，EQ，FP的中点重合，如图：
∴，
解得，
∴P（﹣1，0），Q（1，0），
而F（2，），
∴FQ＝2＝PQ，
∴以E、F、P、Q为顶点的四边形是菱形，
∴P（﹣1，0）；
③当EP，FQ为对角线，EP，FQ的中点重合，如图：
∴，
解得，
∴P（3，0），Q（1，0），
而F（2，），
∴FP＝QP＝2，
∴以E、F、P、Q为顶点的四边形是菱形，
∴P（3，0），
综上所述，P的坐标是（1，6）或（﹣1，0）或（3，0）．
21．（2022春•兴宁区校级期末）如图，抛物线y＝x2+bx+c与x轴交于A（﹣3，0），B（1，0）两点，与y轴交于点C，连接AC，BC，点P是直线AC下方抛物线上的一个动点．
（1）求抛物线的解析式；
（2）连接AP，CP，设P点的横坐标为m，△ACP的面积为S，求S与m的函数关系式；
（3）试探究：过点P作BC的平行线1，交线段AC于点D，在直线l上是否存在点E，使得以点D，C，B，E为顶点的四边形为菱形，若存在，请直接写出点E的坐标，若不存在，请说明理由．
【分析】（1）将A（﹣3，0），B（1，0）代入y＝x2+bx+c即可得到答案；
（2）过点P作PM∥y轴交直线AC于点M，则P的坐标是（m，m2+2m﹣3），利用待定系数法求AC的解析式，表示M的坐标，用m的代数式表示PM的长度，根据三角形面积公式即可得到答案；
（3）分两种情况：①如图2，四边形CDEB是菱形，②如图3，四边形CBDE是菱形，根据两点的距离公式和菱形的边长相等列方程可解答．
【解答】解：（1）将A（﹣3，0），B（1，0）代入y＝x2+bx+c得：，
解得：，
∴y＝x2+2x﹣3；
（2）如图1，过点P作PM∥y轴交直线AC于点M，
∵A（﹣3，0），C（0，﹣3），
设直线AC的解析式为：y＝kx+n，
∴，
∴，
∴AC的解析式为：y＝﹣x﹣3，
∵P点的横坐标为m，
∴P的坐标是（m，m2+2m﹣3），则M的坐标是（m，﹣m﹣3），
∴PM＝﹣m﹣3﹣（m2+2m﹣3）＝﹣m2﹣3m，
∵点P是直线AC下方抛物线上的一个动点，
∴﹣3＜m＜0，
∴S＝•PM•OA＝（﹣m2﹣3m）＝﹣m2﹣m（﹣3＜m＜0）；
（3）分两种情况：
①如图2，四边形CDEB是菱形，
设D（t，﹣t﹣3），则E（t+1，﹣t），
∵四边形CDEB是菱形，
∴CD＝BC，
∴（t﹣0）2+（﹣t﹣3+3）2＝12+32，
∴t＝±，
∵t＜0，
∴t＝﹣，
∴E（﹣+1，）；
②如图3，四边形CBDE是菱形，
设D（t，﹣t﹣3），则E（t﹣1，﹣t﹣6），
∵四边形CBDE是菱形，
∴CE＝BC，
∴（t﹣1﹣0）2+（﹣t﹣6+3）2＝12+32，
∴t＝0（舍）或﹣2，
∴E（﹣3，﹣4）；
综上所述，点E的坐标为（﹣+1，）或（﹣3，﹣4）．
22．如图，已知抛物线y＝ax2+bx﹣2的图象与x轴交于A，B两点，与y轴交于点C．
﹣3和1是关于x的一元二次方程ax2+bx﹣2＝0的两个根．
（1）求该抛物线的解析式；
（2）过点B作BD∥AC交抛物线于点D，BD与y轴交于点E，P为直线AC下方抛物线上的一个动点，连接PB交AC于点F，求S△PEF的最大值及此时点P的坐标；
（3）在（2）的条件下，将该抛物线向右平移2个单位后得到新抛物线，新抛物线与原抛物线相交于点Q，点M为原抛物线对称轴上一点，在平面直角坐标系中是否存在点N，使得以点A，M，N，Q为顶点的四边形是菱形，若存在，请直接写出点N的坐标；如不存在，请说明理由．
【分析】（1）由一元二次方程根与系数的关系列方程组，求出系数a、b的值；
（2）过点P作y轴的平行线，交BD于点G，设点P的横坐标为t，根据S△PEF＝S△BPE﹣S△BEF，和S△BEF＝S△BEC，可得出S△PEF关于x的函数关系式，利用二次函数的性质求出S△PEF的最大值及点P的坐标；
（3）根据平移的性质可得出新抛物线的解析式，联立可得出点Q的坐标，设点M的坐标为（﹣1，m），若以点A，M，N，Q为顶点的四边形是菱形，则需△AMQ为等腰三角形即可．需要分三种情况：AM＝AQ，MA＝MQ，QA＝QM．根据题意列出方程求解即可．
【解答】解：（1）∵﹣3和1是关于x的一元二次方程ax2+bx﹣2＝0的两个根，
∴，解得．
∴该抛物线的解析式为y＝x2+x﹣2．
（2）∵﹣3和1是关于x的一元二次方程ax2+bx﹣2＝0的两个根，抛物线y＝ax2+bx﹣2的图象与x轴交于A，B两点，与y轴交于点C，
当y＝0时，x＝1或x＝﹣3，则A（﹣3，0），B（1，0），
当x＝0时，y＝﹣2，则C（0，﹣2）．
∴直线AC的解析式为：y＝﹣x﹣2，
∵BD∥AC，
∴直线BD的解析式为：y＝﹣x+b′，
∴﹣×1+b′＝0，
∴b′＝，
∴直线BD的解析式为：y＝﹣x+，
令x＝0，则y＝，
∴E（0，）．
∴OB＝1，EC＝，
∴S△BEF＝S△BEC＝EC•OB＝×＝．
过点P作y轴的平行线，交BD于点G，
设点P的横坐标为t，
∴P（t，t2+t﹣2），G（t，﹣t+），
∴S△BPE＝•PG•（xB﹣xE）
＝•[﹣t+﹣（t2+t﹣2）]•1
＝﹣t2﹣t+，
∴S△PEF＝S△BPE﹣S△BEF
＝﹣t2﹣t+﹣
＝﹣t2﹣t
＝﹣（t+）2+．
∵﹣＜0，
∴当t＝﹣时，S△PEF的值最大最大为．
此时P（﹣，﹣）．
（3）存在．理由如下：
由（1）知，原抛物线的解析式为：y＝x2+x﹣2＝（x+1）2﹣．
∴原抛物线的对称轴为（﹣1，0）．
∴将该抛物线向右平移2个单位后得到新抛物线的解析式为：y′＝（x﹣1）2﹣＝x2﹣x﹣2．
令x2+x﹣2＝x2﹣x﹣2，
解得x＝0，
∴Q（0，﹣2）．
∵点M为原抛物线对称轴上一点，
∴设点M的坐标为（﹣1，m），
若以点A，M，N，Q为顶点的四边形是菱形，则需△AMQ为等腰三角形即可，分以下三种情况：
①当AM＝AQ时，
∵A（﹣3，0），Q（0，﹣2），
∴（﹣3+1）2+（0﹣m）2＝（﹣3）2+22，
解得m＝﹣3或3，
∴M（﹣1，3）或M（﹣1，﹣3），
∵以点A，M，N，Q为顶点的四边形是菱形，
∴N（2，1）或N（2，﹣5）．
②当MA＝MQ时，
∵A（﹣3，0），Q（0，﹣2），
∴（﹣3+1）2+（0﹣m）2＝（﹣1）2+（m+2）2，
解得m＝﹣，
∴M（﹣1，﹣），
∵以点A，M，N，Q为顶点的四边形是菱形，
∴N（﹣2，﹣）．
③当QA＝QM时．
∵A（﹣3，0），Q（0，﹣2），
∴（﹣3）2+22＝（﹣1）2+（m+2）2，
解得m＝﹣2+2或m＝﹣2﹣2，
∴M（﹣1，﹣2+2）或M（﹣1，﹣2﹣2），
∵以点A，M，N，Q为顶点的四边形是菱形，
∴N（﹣4，2）或N（﹣4，﹣2）．
综上，存在点N，使得以点A，M，N，Q为顶点的四边形是菱形，此时点N的坐标为N（2，1）或N（2，﹣5）或N（﹣2，﹣）或（﹣4，2）或N（﹣4，﹣2）．
23．如图，已知抛物线y＝ax2+bx﹣3与x轴交于A（﹣1，0），B两点，与y轴交于点C且tan∠ABC＝1，连接AC、BC．
（1）求抛物线的解析式；
（2）若P点是直线BC下方一点，过P点作PE∥AC交BC于点E，PH∥y轴交BC于点H，求CE+BH的最小值及此时P点的坐标．
（3）在第（2）条件下，将该抛物线向右平移2个单位后得到新抛物线，新抛物线与原抛物线相交于点F，点M为原抛物线对称轴上一点，在平面直角坐标系中是否存在点，使得以点H，M，N，F为顶点的四边形是菱形，若存在，请直接写出点N的坐标；如不存在，请说明理由．
【分析】（1）由抛物线y＝ax2+bx﹣3得C（0，﹣3），由tan∠ABC＝1可得OC＝OB，则B（3，0），利用待定系数法将A，B三点坐标分别代入即可求解；
（2）过E点作PM⊥交PH于点M，可得△EMH是等腰直角三角形，EH＝MH＝EM，则EH最大时，CE+BH的值最小，证明△EMP∽△AOC，根据相似三角形的性质可得EM＝PM，设P（m，m2﹣2m﹣3），则H（m，m﹣3），得到PH的长度，继而得到EH长度，根据二次函数的性质即可求解；
（3）存在以点H，M，N，F为顶点的四边形是菱形，分三种情况，即以FH为一边的菱形FHMN；以FH为一边的菱形FHNM；以FH为对角线的矩形FMHN，根据菱形的性质即可求出点P的坐标．
【解答】解：（1）∵抛物线y＝ax2+bx﹣3，
∴C（0，﹣3），
∵tan∠ABC＝1，
∴＝1，
∴OC＝OB，则B（3，0），
把A（﹣1，0）、B（3，0）代入y＝ax2+bx﹣3，
得，解得，
∴该抛物线的解析式为y＝x2﹣2x﹣3；
（2）过E点作PM⊥交PH于点M，
∵OC＝OB，
∴∠OBC＝∠OCB＝45°，
∵PH∥y轴，
∴∠PHC＝∠OCB＝45°，
∴△EMH是等腰直角三角形，
∴EH＝MH＝EM，
∴EH的值最大时，CE+BH的值最小，
∵PE∥AC，
∴∠ACB＝∠PEC，
∵∠OAC＝180°﹣∠ACB﹣∠OBC，∠MEP＝180°﹣∠PEC﹣∠PHC
∴∠OAC＝∠MEP，
∵∠AOC＝∠EMP＝90°，
∴△EMP∽△AOC，
∴，
∴EM＝PM，
∴EM＝MH＝PH．
∵C（0，﹣3），B（3，0），
∴BC＝3，
设直线BC的解析式为y＝kx﹣3，
∴3k﹣3＝0，解得k＝1，
∴直线BC的解析式为y＝x﹣3，
设P（m，m2﹣2m﹣3），则H（m，m﹣3），
∴PH＝m﹣3﹣m2+2m+3＝﹣m2+2m，
∴EH＝MH＝EM＝（﹣m2+2m）＝﹣（m2﹣2m）＝﹣（m﹣）2+，
∴当m＝时，EH的最大值为，
∴CE+BH的最小值为BC﹣EH最大＝3﹣＝，
此时，P点的坐标为（，﹣）；
（3）∵y＝x2﹣2x﹣3＝（x﹣1）2﹣4，
∴抛物线的对称轴为直线x＝1，
将该抛物线向右平移2个单位后得到新抛物线y＝（x﹣1﹣2）2﹣4＝x2﹣6x+5，
∴x2﹣2x﹣3＝x2﹣6x+5，解得x＝2，
∴新抛物线与原抛物线，的交点F（2，﹣3），
由（ 2）知，H（，﹣），
设M（1，t），
①当以FH为一边的菱形FHMN时，MH＝FH，
∵F（2，﹣3），H（，﹣），
∴MH2＝（t+）2+（﹣1）2＝t2+3t+，
FH2＝（2﹣）2+（﹣+3）2＝，
∴t2+3t+＝，解得t＝0（舍去）或﹣3，
∴点M为（1，﹣3），
∴N（，﹣）；
②当以FH为一边的菱形FHNM时，MF＝FH，
∵F（2，﹣3），H（，﹣），
∴MF2＝（t+3）2+（2﹣1）2＝t2+6t+10，
FH2＝（2﹣）2+（﹣+3）2＝，
∴t2+6t+10＝，解得t＝﹣3﹣或﹣3+，
∴点M为（1，﹣3﹣）或（1，﹣3+），
∴N（，﹣﹣）或（，﹣+）；
③当以FH为对角线的矩形FMHN时，MH＝MF，
∵F（2，﹣3），H（，﹣），
∴MF2＝（t+3）2+（2﹣1）2＝t2+6t+10，
MH2＝（t+）2+（﹣1）2＝t2+3t+，
∴t2+6t+10＝t2+3t+，解得t＝﹣，
∴点M为（1，﹣），
∴N（，﹣2）．
综上，点N的坐标为（，﹣）或（，﹣﹣）或（，﹣+）或（，﹣2）．
24．（2022•渝北区自主招生）如图，在平面直角坐标系中，抛物线y＝ax2+bx﹣与x轴交于A、B两点（点A在点B的左侧），与y轴交于点C，点B的坐标为（1，0），且tan∠OAC＝．
（1）求抛物线的解析式；
（2）如图1，点M为直线AC下方抛物线上一点，过点M作MD∥y轴交AC于点D，求MD+DC的最大值及此时点M的坐标；
（3）如图2，连接BC，将△BOC绕着点A逆时针旋转60°得到△B'O'C'，将抛物线y＝ax2+bx﹣沿着射线CB方向平移，使得平移后的新抛物线经过O'，H是新抛物线对称轴上一点，在平面直角坐标系中是否存在点P，使以点B'，C'，H，P为顶点的四边形是以B'C'为边的菱形，若存在，请直接写出点P的坐标；若不存在，请说明理由．
【分析】（1）利用三角形函数的正切值，求出OA，从而确定A点坐标，再由待定系数法求函数的解析式即可；
（2）求出直线AC的解析式，设M（t，t2+t﹣），则D（t，﹣t﹣），则MD＝﹣t2﹣t，过点D作DE⊥y轴交于点E，利用直角三角形的三角函数值求出CD＝﹣t，则MD+CD＝﹣（t+）2+，当t＝﹣时，MD+CD的最大值为，
（3）连接AO'，OO'，过点O'作O'H⊥x轴交于点H，由旋转可知，△AOO'是等边三角形，可求O'（﹣，），设抛物线沿x轴正方向平移m个单位，则沿y轴正方向平移m个单位，平移后的抛物线解析式为y＝（x+1﹣m）2﹣+m，再将O'代入抛物线解析式可得m＝，则抛物线的解析式为y＝（x﹣）2+，设H（，t），P（x，y），连接BB'、AB'，AC、AC'，分别在等边三角形△ACC'、△ABB'中求出C'（0，），B'（﹣1，2），再分两种情况讨论：①当B'H为菱形的对角线时，B'C'＝C'H，求得P（﹣，+2）或（﹣，﹣+2）；②当B'P为菱形的对角线时，B'C'＝B'H，求得P（，+）或（，﹣+）．
【解答】解：（1）令x＝0，则y＝﹣，
∴C（0，﹣），
∴OC＝，
∵tan∠OAC＝，
∴OA＝3，
∴A（﹣3，0），
将A（﹣3，0），B（1，0）代入y＝ax2+bx﹣，
∴，
解得，
∴y＝x2+x﹣；
（2）设直线AC的解析式为y＝kx+b，
∴，
解得，
∴y＝﹣x﹣，
设M（t，t2+t﹣），则D（t，﹣t﹣），
∴MD＝﹣t﹣﹣t2﹣t+＝﹣t2﹣t，
过点D作DE⊥y轴交于点E，
∵tan∠ACO＝＝，
∴∠ACO＝60°，
∴CD＝＝ED，
∵DE＝﹣t，
∴CD＝﹣t，
∴MD+CD＝﹣t2﹣t﹣t＝﹣t2﹣t＝﹣（t+）2+，
∴当t＝﹣时，MD+CD的最大值为，
此时M（﹣，﹣）；
（3）存在点P，使以点B'，C'，H，P为顶点的四边形是以B'C'为边的菱形，理由如下：
设直线BC的解析式为y＝kx+b，
∴，
解得，
∴y＝x﹣，
连接AO'，OO'，过点O'作O'H⊥x轴交于点H，
由旋转可知，AO＝AO'＝3，∠OAO'＝60°，
∴△AOO'是等边三角形，
∴OH＝，O'H＝，
∴O'（﹣，），
设抛物线沿x轴正方向平移m个单位，则沿y轴正方向平移m个单位，
∴平移后的抛物线解析式为y＝（x+1﹣m）2﹣+m，
∵O'在新抛物线上，
∴＝（﹣+1﹣m）2﹣+m，
解得m＝或m＝﹣（舍），
∴抛物线的解析式为y＝（x﹣）2+，
∴抛物线的对称轴为直线x＝，
设H（，t），P（x，y），
连接BB'、AB'，AC、AC'，
在△ACC'中，AC＝AC'，∠CAC'＝60°，
∴△ACC'是等边三角形，
∵∠CAO＝30°，
∴C'与C关于AO对称，
∴C'（0，），
在△ABB'中，AB＝AB'，∠BAB'＝60°，
∴△ABB'是等边三角形，
∵A（﹣3，0），B（1，0），
∴AB＝4，
∴B'（﹣1，2），
①当B'H为菱形的对角线时，B'C'＝C'H，
∴，
解得或，
∴P（﹣，+2）或（﹣，﹣+2）；
②当B'P为菱形的对角线时，B'C'＝B'H，
∴，
解得或，
∴P（，+）或（，﹣+）；
综上所述：（﹣，+2）或（﹣，﹣+2）或（，+）或（，﹣+）．