山东省烟台市2023届九年级中考一模数学试卷(含解析)

这是一份山东省烟台市2023届九年级中考一模数学试卷(含解析)，共24页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

1. - 9的倒数是( )
A. -19B. 19C. -3D. -13
2. 下列计算正确的是( )
A. x3⋅x2=x5B. x3÷(-x2)=xC. x3-x2=xD. 2x+x=3x2
3. 若用我们数学课本上采用的科学计算器进行计算，依次按键，对应的计算是( )
A. 23B. 32C. 33D. 3
4. 按如图所示的程序进行计算，若输入x的值为6，则输出y的值为( )
A. 2B. 2+ 2C. 2- 2D. 6-4 2
5. 一名射击运动员统计了45次射击成绩，并绘制了如图所示的折线统计图，关于这组数据下列说法不正确的是( )
A. 中位数是8B. 众数是8C. 平均数是8D. 方差是1.3
6. 如图，在方格纸中，△ABC和△DEF的顶点都在格点上，则∠BAC+∠ACB的度数为( )
A. 30°
B. 45°
C. 60°
D. 75°
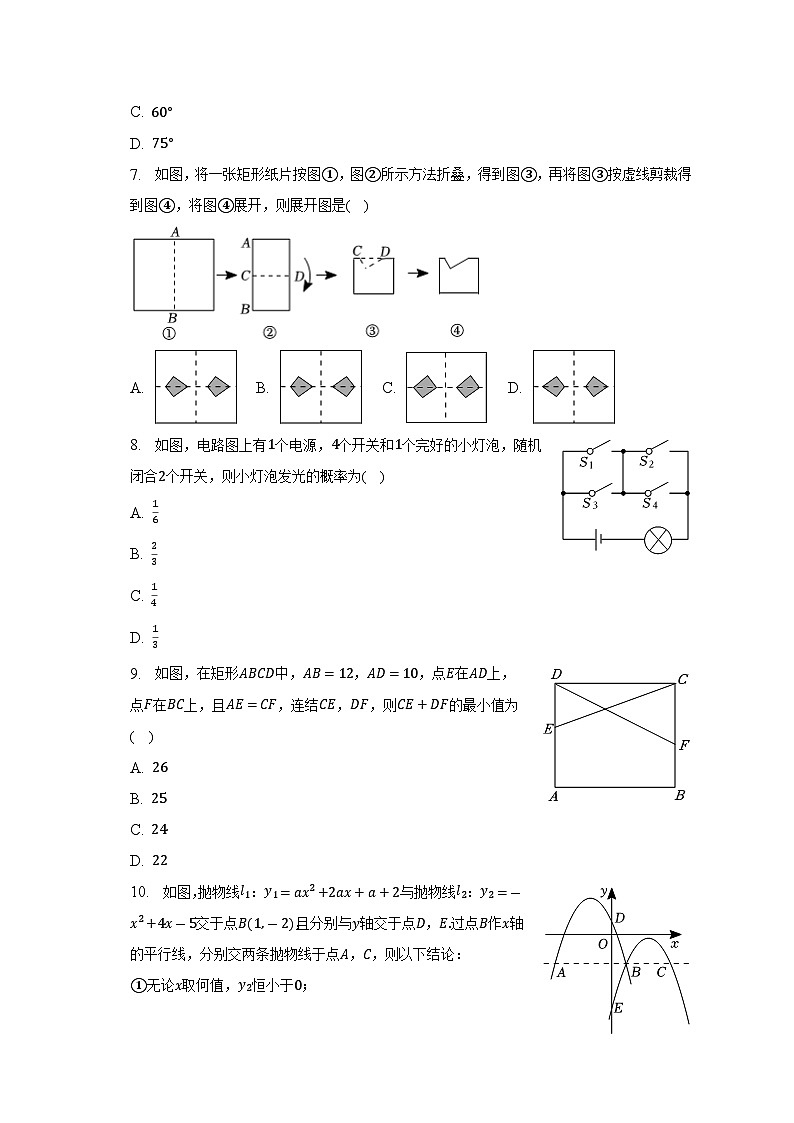
7. 如图，将一张矩形纸片按图①，图②所示方法折叠，得到图③，再将图③按虚线剪裁得到图④，将图④展开，则展开图是( )
A. B. C. D.
8. 如图，电路图上有1个电源，4个开关和1个完好的小灯泡，随机闭合2个开关，则小灯泡发光的概率为( )
A. 16
B. 23
C. 14
D. 13
9. 如图，在矩形ABCD中，AB=12，AD=10，点E在AD上，点F在BC上，且AE=CF，连结CE，DF，则CE+DF的最小值为( )
A. 26
B. 25
C. 24
D. 22
10. 如图，抛物线l1：y1=ax2+2ax+a+2与抛物线l2：y2=-x2+4x-5交于点B(1,-2)，且分别与y轴交于点D，E.过点B作x轴的平行线，分别交两条抛物线于点A，C，则以下结论：
①无论x取何值，y2恒小于0；
②l1可由l2向右平移3个单位长度，再向下平移3个单位长度得到；
③当-2④四边形AECD的面积为18．
其中正确的有( )
A. 1个B. 2个C. 3个D. 4个
二、填空题（本大题共6小题，共18.0分）
11. 如图，李大爷要建一个矩形羊圈，羊圈的一边利用长为12m的住房墙，另外三边用25m长的彩钢围成，为了方便进出，在垂直于住房墙的一边留了一扇1m宽的门.若要使羊圈的面积为80m2，则所围矩形与墙垂直的一边长为______ m.
12. 如图，点A，B在反比例函数y=kx(x<0)的图象上，延长AB与x轴负半轴交于点C，连接OA，若点B是AC的中点，△AOC的面积等于9，则k的值为______ ．
13. 两个平面镜OM和ON如图摆放，从点A处向平面镜ON射出一束平行于OM的光线，经过两次反射后，光线CD与平面镜ON垂直，则两平面镜的夹角∠MON的度数为______ ．
14. 对于正数x，规定f(x)=x1+x，例如f(2)=21+2=23，则f(12023)+f(12022)+⋅⋅⋅+f(12)+f(1)+f(2)+⋅⋅⋅+f(2023)的值是______ ．
15. 关于x的一元二次方程x2-4x+m-1=0的两个实数根是x1，x2，满足x12-4x1+3x1x2>2，则m的取值范围是______ ．
16. 如图，GC，GB是⊙O的切线，AB是⊙O的直径，延长GC，与BA的延长线交于点E，过点C作弦CD//AB，连接DO并延长与圆交于点F，连接CF，若AE=2，CE=4，则CD的长度为______ ．
三、解答题（本大题共8小题，共64.0分。解答应写出文字说明，证明过程或演算步骤）
17. (本小题8.0分)
求不等式组4(x-1)≤2(x+3)x-13-12x<-1的整数解．
18. (本小题8.0分)
如图所示，是一个迷宫示意图，小明和小亮分别从入口进入，沿着虚线所示的路线行走，两人根据自己的选择随机进入A，B，C三个房间中的某一个．
(1)小明进入A房间的概率是多少？
(2)利用树状图或表格，求出两人在走迷宫结束后，B房间至少有1个人的概率．
19. (本小题8.0分)
如图，△ABC中，AB=AC，∠A=36°，以点B为圆心，BC为半径画弧，交AC于点D，连接BD，过点B平行于AC的直线与过点D平行于AB的直线交于点E，连接CE，求∠CED的度数．
20. (本小题8.0分)
A，B两地之间的国道的长度为180千米．
(1)甲、乙两人均要从A地前往B地.乙乘公交车先走了20千米，甲才开车从A地出发，甲出发40分钟后刚好追上乙.已知甲开车的速度是乙所乘公交车速度的1.5倍，求乙所乘公交车的速度；
(2)高速公路修通后，高速公路的全长比原来国道长减少了40千米，某长途汽车在高速公路上的行驶速度比在国道上提高了35千米/时，从A地到B地的行驶时间缩短了一半，求该长途汽车在原来国道上行驶的速度．
21. (本小题8.0分)
如图，在△ABC中，AB=AC，以AC为直径的⊙O交AB边于点D，过点B作BE//AC，与过点C的切线交于点E，连接CD．
(1)求证：CD=CE；
(2)若AC=5、BD=2，求BC的长．
22. (本小题8.0分)
梨花节期间，为了更好地记录梨乡美景，摄影协会特意请一名摄影师携带无人机进行航拍.如图，摄影师在水平地面上点O处测得无人机位置点B的仰角为56°；当摄影师迎着坡度为3：4的斜坡从点O走到点A时，无人机的位置恰好从点B水平飞到点C，此时，摄影师在点A处测得点C的仰角∠CAP=45°，若OA=5米，BC=6米，无人机与水平地面之间的距离始终保持不变，且O、A、B、C四点在同一平面内，求无人机距水平地面的高度.(结果精确到0.1m，参考数据：sin56°≈0.83，cs56°≈0.56，tan56°≈1.48)
23. (本小题8.0分)
问题引入：如图①，AB//CD，AB>CD，∠ABD=90°，E是线段AC的中点．连结DE并延长交AB于点F，连结BE.判断BE与DE之间的数量关系，并说明理由．
问题延伸：如图②，在正方形ABCD和正方形BEFG中，点A、B、E在同一条直线上，点G在BC上，P是线段DF的中点，连结PC、PG．
(1)判断PC与PG之间的数量关系，并说明理由．
(2)连结CF，若AB=3，PC= 2，则CF的长为______．
24. (本小题8.0分)
如图，抛物线y=ax2+bx+c经过点A(-2,0)，点B(4,0)，交y轴于点C(0,4).连接AC，BC.D为OB上的动点，过点D作ED⊥x轴，交抛物线于点E，交BC于点G．

(1)求这条抛物线的表达式；
(2)过点E作EF⊥BC，垂足为点F，设点D的坐标为(m,0)，请用含m的代数式表示线段EF的长，并求出当m为何值时EF有最大值，最大值是多少？
(3)点D在运动过程中，是否存在这样的点G，使得以O，D，G为顶点的三角形与△AOC相似.若存在，请求出此时点G的坐标；若不存在，请说明理由．
答案和解析
1.答案：D
解析：解：∵- 9=-3，
∴- 9的倒数等于-13．
故选：D．
先化简- 9，再求倒数即可．
本题考查了算术平方根的意义及倒数的定义，根据算术平方根的定义正确化简- 9是解答本题的关键．
2.答案：A
解析：解：A.x3⋅x2=x5，故选项正确，符合题意；
B.x3÷(-x2)=-x3+2=-x5，故选项错误，不符合题意；
C.x3，x2不是同类项，不能合并，故选项错误，不符合题意；
D.2x+x=3x，故选项错误，不符合题意．
故选：A．
根据同底数幂相乘，同底数幂相除，合并同类项的运算法则计算即可得解．
本题考查了同底数幂相乘，同底数幂相除，合并同类项的运算法则，解题的关键是熟练掌握运算法则．
3.答案：D
解析：解：根据按键顺序可知算式为 3．
故选：D．
根据按键的顺序即可得出算式．
本题考查了科学计算器的使用与平方根，掌握“2ndF”与“平方根”键组合表示求一个数的平方根是关键．
4.答案：A
解析：解：把x=6代入，得6÷3- 2=2- 2，
∵2- 2<1，
∴y=(2- 2)(2+ 2)=2．
故选：A．
把x=6代入程序流程图进行计算即可．
本题考查了程序设计与实数运算，解题的关键是按照题中箭头的方向依次计算，遇到判断框时，注意判断清楚满足哪个路径的要求．
5.答案：D
解析：解：由图可知，将45次射击成绩，从小到大依次排列，第23个数为8环，故中位数是8，A选项正确，不符合题意；
8环出现次数最多，有18次，故众数为8，B选项正确，不符合题意；
这组数据的平均数为145×(6×5+8×7+18×8+10×9+4×10)=8，故C选项正确，不符合题意；
这组数据的方差为145[5×(6-8)2+8×(7-8)2+18×(8-8)2+10×(9-8)2+4×(10-8)2]=1.2，故D选项不正确，符合题意．
故选：D．
读懂折线统计图，根据中位数，众数，平均数，方差的定义求解即可．
本题考查了折线统计图，中位数，众数，平均数，方差，读懂折线图，熟练掌握中位数，众数，平均数，方差的定义是解题的关键．
6.答案：B
解析：解：∵AB= 12+22= 5,BC= 12+32= 10,AC=5，
DE= 12+12= 2,EF=2,DF= 12+32= 10，
∵ 5 2= 102=5 10，
∴ABDE=BCEF=ACDF，
∴△ABC∽△DEF，
∴∠ABC=∠DEF=135°，
∴∠BAC+∠ACB=180°-135°=45°，
故选：B．
根据网格的特点，利用勾股定理求得△ABC、△EDF各边长，进而证明△ABC∽△DEF，根据相似三角形的性质得出∠ABC=∠DEF=135°，即可求解．
本题考查了勾股定理的逆定理，勾股定理，相似三角形的判定与性质，熟练掌握其性质是解决此题的关键．
7.答案：D
解析：解：严格按照图中的顺序向右翻折，向下翻折，按按虚线剪裁，展开得到结论，
故选：D．
对于此类问题，亲自动手操作，即可得出答案．
本题考查了剪纸问题，此类题目主要考查学生的动手能力及空间想象能力，对于此类问题，学生只要亲自动手操作，答案就会很直观地呈现．
8.答案：B
解析：解：画树状图如下：

共有12种等可能的结果，其中随机闭合2个开关，小灯泡发光的结果有：S1S2，S1S4，S2S1，S2S3，S3S2，S3S4，S4S1，S4S3，共8种，
∴随机闭合2个开关，小灯泡发光的概率为812=23．
故选：B．
画树状图得出所有等可能的结果数和随机闭合2个开关，小灯泡发光的的结果数，再利用概率公式可得出答案．
本题考查列表法与树状图法，熟练掌握列表法与树状图法以及概率公式是解答本题的关键．
9.答案：A
解析：解：如图，连接BE，
∵四边形ABCD是矩形，
∴AB=CD，∠BAE=∠DCF=90°，
∵AE=CF，
∴△ABE≌△CDF，
∴BE=DF，
∴CE+DF=CE+BE，
如图，作点B关于A点的对称点B'，连接CB'，
CB'即为CE+BE的最小值，
∵AB=12，AD=10，
∴BB'=24，BC=10，
∴CB'= BB'2+BC2=26，
∴CE+DF的最小值为26，故A正确．
故选：A．
先连接BE，将CE+DF转化为CE+BE，再利用将军饮马解决问题即可．
本题考查矩形的性质、勾股定理、将军饮马问题、全等三角形的判定与性质等内容，综合性较强，将CE+DF转化为CE+BE是解题的关键．
10.答案：C
解析：解：①∵(x-2)2≥0，
∴-(x-2)2≤0，
∴y2=-(x-2)2-1≤-1<0，
∴无论x取何值，y2总是负数；
故①正确；
②∵抛物线l1：y1=a(x+1)2+2与l2：y2=-(x-2)2-1交于点B(1,-2)，
∴当x=1时，y=-2，
即-2=a(1+1)2+2，
解得：a=-1；
∴y1=-(x+1)2+2，
∴l2可由l1向右平移3个单位，再向下平移3个单位得到；
故②正确；
③∵y1-y2=-(x+1)2+2-[-(x-2)2-1]=-6x+6，
∴随着x的增大，y1-y2的值减小；
故③错误；
④设AC与DE交于点F，
∵当y=-2时，-(x+1)2+2=-2，
解得：x=-3或x=1，
∴点A(-3,-2)，
当y=-2时，-(x-2)2-1=-2，
解得：x=3或x=1，
∴点C(3,-2)，
∴AF=CF=3，AC=6，
当x=0时，y1=1，y2=-5，
∴DE=6，DF=EF=3，
∴四边形AECD为平行四边形，
∴AC=DE，
∴四边形AECD为矩形，
∵AC⊥DE，
∴四边形AECD的面积=6×8=48．
故④正确．
故选：C．
①由非负数的性质，即可证得y2=-(x-2)2-1≤-1<0，即可得无论x取何值，y2总是负数；
②由抛物线l1：y1=a(x+1)2+2与l2：y2=-(x-2)2-1交于点B(1,-2)，可求得a的值，然后由抛物线的平移的性质，即可得l2可由l1向右平移3个单位，再向下平移3个单位得到；
③由y1-y2=-(x+1)2+2-[-(x-2)2-1]=-6x+6，可得随着x的增大，y1-y2的值减小；
④首先求得点A，C，D，E的坐标，即可证得AF=CF=DF=EF，又由AC⊥DE，即可证得四边形AECD为正方形．
此题考查了待定系数法求二次函数的解析式、非负数的性质、二次函数的平移以及正方形的判定．此题难度较大，注意掌握方程思想与数形结合思想的应用．
11.答案：8
解析：解：设所围矩形与墙垂直的一边长为x m，则与墙平行的一边长为(25+1-2x)m，
根据题意得：x(25+1-2x)=80，
整理得：x2-13x+40=0，
解得：x1=5，x2=8，
当x=5时，25+1-2x=25+1-2×5=16>12，不符合题意，舍去；
当x=8时，25+1-2x=25+1-2×8=10<12，符合题意，
∴x=8，
∴所围矩形与墙垂直的一边长为8m．
故答案为：8．
设所围矩形与墙垂直的一边长为xm，则与墙平行的一边长为(25+1-2x)m，根据羊圈的面积为80m2，可得出关于x的一元二次方程，解之取其符合题意的值，即可得出结论．
本题考查了一元二次方程的应用，找准等量关系，正确列出一元二次方程是解题的关键．
12.答案：-6
解析：解：过A作AD⊥OC，过B作BE⊥OC，分别交OC于点D，E，则BE//AD，
∴△ADC∽△BEC，
∴CBCA=BEAD，
∵B为AC的中点，
∴CBCA=BEAD=12，
∴CE=12CD=DE，

∵点A，B在反比例函数y=kx(k≠0)的图象上，
∴S△ODA=S△OEB，即：12OD⋅AD=12OE⋅BE，
∵AD=2BE，
∴OE=2OD，
∴OD=DE，
∴OC=3OD，
∴S△AODS△AOC=12OD⋅AD12OC⋅AD=13，
∴S△AOD=13S△AOC=13×9=3，
∴k=-2S△AOD=-2×3=-6．
故答案为：-6．
过A作AD⊥OC，过B作BE⊥OC，得到△ADC∽△BEC，根据k的几何意义和B为AC的中点，得到OD=DE=CE，再根据△AOC的面积为9，求出△AOD的面积即可解答．
本题主要考查了已知图形的面积求k值，掌握反比例函数中k的几何意义、构造与k有关的几何图形是解题的关键．
13.答案：30°
解析：解：设∠MON=x，
∵AB//OM，
∴∠ABN=∠MON=x．
由题意得：∠ABN=∠OBC=x，
∵∠BCM是△OBC的一个外角，
∴∠BCM=∠MON+∠OBC=2x，
由题意得：∠DCO=∠BCM=2x，
∵CD⊥ON，
∴∠ODC=90°，
∴∠MON+∠DCO=90°，
∴x+2x=90°，
∴x=30°，
∴∠MON=30°．
故答案为：30°．
设∠MON=x，根据平行线的性质可得∠ABN=x，由题意得：∠ABN=∠OBC=x，∠DCO=∠BCM，再利用三角形的外角得∠DCO=2x，然后利用垂直的定义可得∠ODC=90°，从而利用直角三角形的两个锐角互余进行计算即可得出答案．
本题考查了平行线的性质以及三角形外角的性质，熟练掌握性质定理是解题的关键．
14.答案：2022.5
解析：解：∵f(x)=x1+x，
∴f(1x)=1x1+1x=11+x，
∴f(x)+f(1x)=11+x+x1+x=1+x1+x=1，
∴f(12023)+f(12022)+⋅⋅⋅+f(12)+f(1)+f(2)+⋅⋅⋅+f(2023)
=[f(2023)+f(12023)]+[f(2022)+f(12022)]+⋯+[f(2)+f(12)]+f(1)
=1×(2023-1)+11+1
=2022+12
=2022.5，
故答案为：2022.5．
根据已知规定，可得f(x)+f(1x)=1，进而可以解决问题．
本题主要考查了新定义下的实数运算，分式的加减计算，正确理解题意得到f(x)+f(1x)=1是解题的关键．
15.答案：2解析：解：∵关于x的一元二次方程x2-4x+m-1=0的两个实数根是x1，x2，
∴x12-4x1+m-1=0，x1x2=ca=m-11=m-1，
∴x12-4x1=1-m，
∴x12-4x1+3x1x2=1-m+3(m-1)=2m-2．
∵x12-4x1+3x1x2>2，
∴2m-2>2，
解得：m>2．
∵该方程有两个实数根，
∴Δ=b2-4ac=(-4)2-4(m-1)≥0，
解得：m≤5，
∴2故答案为：2根据题意可得出x12-4x1+m-1=0，x1x2=m-1，整体代入x12-4x1+3x1x2>2，即可求出m>2.再根据一元二次方程有两个实数根时，其根的判别式Δ≥0，可求出m≤5，最后取其公共解即可．
本题考查一元二次方程的解的定义，一元二次方程根与系数的关系，根据一元二次方程的解的情况求参数．掌握一元二次方程ax2+bx+c=0(a≠0)的根的判别式为Δ=b2-4ac，且当Δ>0时，该方程有两个不相等的实数根；当Δ=0时，该方程有两个相等的实数根；当Δ<0时，该方程没有实数根．熟记一元二次方程根与系数的关系：x1+x2=-ba和x1⋅x2=ca是解题关键．
16.答案：185
解析：解：如图，设CF交AB于点H，连接OC，

∵GC是⊙O的切线，
∴OC⊥GE，
∴∠OCE=90°，
设⊙O的半径为r，则OC=r，OE=r+2，
在Rt△OCE中，
由勾股定理得，OC2+CE2=OE2即r2+42=(r+2)2，
解得：r=3，
∵DF为直径，
∴∠DCF=90°，
∵CD//AB，
∴∠CHE=∠DCF=90°，
∴CF⊥AB，
∴CH=FH，
∵12CH⋅OE=12OC⋅CE，
∴CH=3×45=125，
∴CF=2CH=245，
在Rt△DCF中，
由勾股定理得，
CD= DF2-CF2= 62-(245)2=185，
故答案为：185．
设CF交AB于点H，连接OC，由切线的性质得∠OCE=90°，设⊙O的半径为r，则OC=r，OE=r+2，由勾股定理求得r=3，再根据圆周角定理得∠DCF=90°，由平行线的性质推出CF⊥AB，利用垂径定理可得CH=FH，由三角形的面积求得CH，再求出CF，利用勾股定理求得CD即可．
本题考查了切线的性质，圆周角定理，垂径定理，勾股定理，熟练掌握知识点并灵活运用是解题的关键．
17.答案：解：4(x-1)≤2(x+3)①x-13-12x<-1②，
解不等式①，得：x≤5，
解不等式②，得：x>4，
∴该不等式组的解集为4∴该不等式组的整数解为5．
解析：分别解出每一个不等式的解集，再根据“同大取大，同小取小，大小小大中间找，大大小小找不到”的原则确定该不等式组的解集，进而即可得出其整数解．
本题考查求不等式组的整数解．掌握求不等式组解集的原则“同大取大，同小取小，大小小大中间找，大大小小找不到”是解题关键．
18.答案：解：(1)共有3个房间，小明进入A房间的概率为13；
(2)列表如下
由表格可知，共有9种等可能性发生的结果，其中B房间至少有1个人的结果共有5种，
所以B房间至少有1个人的概率为59，
解析：(1)根据概率公式直接求解即可；
(2)根据列表法求概率即可求解．
本题考查了概率公式求概率，列表法求概率，熟练掌握概率的求法是解题的关键．
19.答案：解：∵AB=AC，∠A=36°，∠A+∠BCD+∠ABC=180°，
∴∠BCD=∠ABC=72°，
∵AB//DE，
∴∠CDE=∠A=36°，
∵AC//BE，
∴∠BED=∠CDE=36°，∠CBE=∠BCD=72°，
∵BC=BD，
∴∠CDE+∠BDE=∠BCD=72°，
∴∠BDE=36°，
∴∠BDE=∠BED，
∴BD=BE，
∴BC=BE，
∴∠CEB=∠BCE，
∵∠CEB+∠BCE+∠CBE=180°，
∴∠CEB=54°，
∴∠CED=∠CEB-∠BED=54°-36°=18°．
解析：根据等腰三角形的性质以及三角形内角和定理求得∠BCD=∠ABC=72°，再利用平行线的性质可求得∠CBE=∠BCD=72°，最后利用等腰三角形的性质和三角形内角和推出∠CEB=54°，即可求解．
本题考查了等腰三角形的判定与性质，平行线的性质，三角形内角和定理，正确的识别图形并会探索角之间的关系是解题的关键．
20.答案：解：(1)设乙所乘公交车的速度为x千米/小时，则甲开车的速度为1.5千米/小时，
由题意得：1.5x×4060=20+4060x，
解得：x=60，
答：乙所乘公交车的速度为60千米/小时；
(2)设该长途汽车在原来国道上行驶的速度为y千米/小时，则该长途汽车在高速公路上行驶的速度为(x+35)千米/小时，
由题意得：180-40x+35=180x×12，
解得：x=63，
经检验，x=63是原方程的解，且符合题意，
答：该长途汽车在原来国道上行驶的速度为63千米/小时．
解析：(1)设乙所乘公交车的速度为x千米/小时，则甲开车的速度为1.5千米/小时，由题意：乙乘公交车先走了20千米，甲才开车从A地出发，甲出发40分钟后刚好追上乙．列出一元一次方程，解方程即可；
(2)设该长途汽车在原来国道上行驶的速度为y千米/小时，由题意：某长途汽车在高速公路上的行驶速度比在国道上提高了35千米/时，从A地到B地的行驶时间缩短了一半，列出分式方程，解方程即可．
本题考查了一元一次方程的应用以及分式方程的应用，解题的关键是：(1)找准等量关系，正确列出一元一次方程；(2)找准等量关系，正确列出分式方程．
21.答案：(1)证明：∵AC是⊙O的直径，
∴∠CDA=90°，
∴CD⊥AB，∠BDC=90°，
∵CE切⊙O于C，
∴AC⊥CE，
∵BE//AC，
∴BE⊥CE，∠EBC=∠ACB，
∵AB=AC，
∴∠ACB=∠ABC，
∴∠ABC=∠EBC，
∵CD⊥AB，CE⊥BE，
∴CD=CE；
(2)解：∵AC=5，AB=AC，
∴AB=5，
∵BD=2，
∴AD=5-2=3，
由勾股定理得：CD= AC2-AD2=4，
由勾股定理得：BC= BD2+CD2=2 5．
解析：(1)根据圆周角定理求出CD⊥AB，∠BDC=90°，根据切线的性质得出AC⊥CE，求出∠DBC=∠EBC，根据角平分线性质得出即可；
(2)求出AC=5，BD=2，根据勾股定理求出CD，再根据勾股定理求出BC即可．
本题考查了切线的性质，勾股定理，角平分线性质，等腰三角形的判定等知识点，能综合运用定理进行推理是解此题的关键．
22.答案：解：过A作AD⊥地面于D，
∵OA坡度为3：4，
设AD=3h，则OD=4h，
∵OA=5，
∴AD2+OD2=OA2，即(3h)2+(4h)2=52，
∴h=1，
∴AD=3，OD=4，
过B作BE⊥地面于E，交AP于F，交AC于G，过C作CM⊥地面于M，交AP于N，

∵∠CAP=45°，
∴△AFG和△ANC均为等腰直角三角形，
∴AF=GF，AN=CN，
设AF=x米，则GF=x米，
∵BC//AP，且∠BFN=∠CNF=90°，
∴四边形BCNF为矩形，
∴FN=BC=6，BF=CN=AN=6+x，
∵FE=AD=3，
∴BE=BF+FE=6+x+3=9+x，OE=OD+DE=4+x，
∵∠BOM=56°，tan∠BOM=BEOE=tan56°=1.48，
∴9+x=1.48×(4+x)，
解得：x≈6.4，
∴BE≈9+6.4=15.4米，
答：无人机距水平地面的高度约为15.4米．
解析：过A作AD⊥地面于D，求得AD=3，OD=4，过B作BE⊥地面于E，交AP于F，交AC于G，过C作CM⊥地面于M，交AP于N，设AF=x，则GF=x，证明四边形BCNF为矩形，FN=BC=6，BF=CN=AN=6+x，由FE=AD=3推出BE=BF+FE=6+x+3=9+x，OE=OD+DE=4+x，根据tan56°≈1.48，解得x的值，进一步求解即可．
此题考查解直角三角形的实际应用，解题的关键是恰当引出辅助线构造直角三角形，以及熟记各三角函数的计算公式．
23.答案： 5
解析：解：问题引入：
BE=DE，理由如下：
∵AB//CD，
∴∠A=∠C，
∵E是AC的中点，
∴AE=CE，
在△AEF和△CED中，
∠A=∠CAE=CE∠AEF=∠CED，
∴△AEF≌△CED(ASA)，
∴EF=DE，
∵∠ABD=90°，
∴BE为Rt△BDF斜边上的中线，
∴EF=DE=BE，
∴BE=DE；
问题延伸：
(1)PC=PG，理由如下：
如图，延长GP交CD于点M，

∵四边形ABCD，BEFG为正方形，
∴CD//AE//GF，∠BCD=90°，
∴∠CDP=∠PFG，
∵P为DF的中点，
∴DP=FP，
在△DPM和△FPG中，
∠MDP=∠GFPDP=FP∠DPM=∠FPG，
∴△DPM≌△FPG(ASA)，
∴PM=PG，GF=DM，
∵PC为Rt△MCG斜边上的中线，
∴PC=PG=PM，
∴PC=PG；
(2)∵四边形ABCD、BEFG为正方形，
∴AB=BC=CD=3，BG=GF=DM，∠CGF=90°，
设BG=GF=DM=x，
∴CM=CG=3-x，
∵PC=PG=PM= 2，
∴MG=2 2，
∵MC2+CG2=MG2，
∴(3-x)2+(3-x)2=(2 2)2，
解得x=1，
∴GF=1，CG=3-1=2，
∴CF= GF2+CG2= 12+22= 5．
故答案为： 5．
问题引入：
利用ASA证明△AEF≌△CED，可得EF=DE，进而可以解决问题；
问题延伸：
(1)延长GP交CD于点M，根据正方形的性质证明△DPM≌△FPG(ASA)，可得PM=PG，GF=DM，根据PC为Rt△MCG斜边上的中线，进而可以解决问题；
(2)根据正方形的性质设BG=GF=DM=x，可得CM=CG=3-x，然后利用勾股定理即可解决问题．
本题考查了正方形的性质的运用，矩形的性质的运用，全等三角形的判定及性质的运用，勾股定理，证明三角形全等是解答本题的关键．
24.答案：解：(1)由题意得4a-2b+c=016a+4b+c=0c=4，
∴a=-12b=1c=4，
∴y=-12x2+x+4；
(2)设直线BC的表达式为y=kx+n，
∵过点B(4,0)，C(0,4)，
∴4k+n=0n=4，
∴k=-1n=4，
∴直线BC的表达式为y=-x+4，
∴点E的坐标为(m,-12m2+m+4)，点G的坐标为(m,-m+4)，
∴EG=-12m2+m+4-(-m+4)=-12m2+2m，
∵OC=OB=4，
∴∠OBC=45°，
∵ED⊥x轴，
∴∠BGD=45°，
∴∠EGF=45°，
∵EF⊥BC，
∴EF= 22EG=- 24m2+ 2m=- 24(m-2)2+ 2，
∴当m=2时，EF有最大值 2；
(3)存在
∵OC=4，OA=2，G的坐标为(m,-m+4)，∠COA=∠ODG=90°，
∴①当△OAC∽△DOG时，DGDO=OCOA=2，
即-m+4m=2，
解得m=43，
此时G的坐标为(43,83)，
②当△OAC∽△DGO时，DGDO=OAOC=12，
即-m+4m=12，
解得m=83，
此时G的坐标为(83,43)，
所以，G点坐标为(43,83)或(83,43)
解析：(1)将A(-2,0)，B(4,0)，C(0,4)代入y=ax2+bx+c，即可求解；
(2)利用待定系数法求出直线BC的表达式，即可表示出点E和点G的坐标，从而得出EG再根据解直角三角形求得EF，根据二次函数的最值即可得出答案；
(3)分△OAC∽△DOG和△OAC∽△DGO两种情况，根据相似三角形的性质得出线段之间的关系求得m的值，从而求得点G的坐标．
本题考查了二次函数的性质及相似三角形的判定及性质，熟练掌握性质定理是解题的关键．
小亮小明
A
B
C
A
(A,A)
(A,B)
(A,C)
B
(B,A)
(B,B)
(B,C)
C
(C,A)
(C,B)
(C,C)