期末仿真测试卷（扬州专用）-2023-2024学年八年级数学下学期期末复习培优拔高（苏科版）

这是一份期末仿真测试卷（扬州专用）-2023-2024学年八年级数学下学期期末复习培优拔高（苏科版），文件包含期末仿真测试卷扬州专用原卷版docx、期末仿真测试卷扬州专用解析版docx等2份试卷配套教学资源，其中试卷共30页， 欢迎下载使用。

（满分：150分 时间：120分钟）
一．选择题（共9小题，满分27分，每小题3分）
1．（3分）下列图形中是中心对称图形但不是轴对称图形的是（ ）
A．B．C．D．
试题分析：根据轴对称图形与中心对称图形的概念求解．
答案详解：解：A、不是中心对称图形，是轴对称图形，不合题意；
B、是中心对称图形，不是轴对称图形，符合题意；
C、不是中心对称图形，是轴对称图形，不合题意；
D、不是中心对称图形，也是轴对称图形，不合题意．
所以选：B．
2．（3分）2022年10月12日，“天宫课堂”第三课在中国空间站开讲．这也是中国航天员首次在问天实验舱内进行授课．微重力环境下毛细效应实验、水球变“濑”实验、太空趣味饮水、会调头的扳手、植物生长研究项目介绍……来自全国各地的青少年，一同收看了这场来自400公里之上的奇妙科学课．某校为了解学生观看“天宫课堂”的情况，随机抽取了300名学生参加“你最喜爱的一项太空实验”的问卷调查，下列说法正确的是（ ）
A．这是一次普查
B．总体是300名学生
C．个体是每名学生的问卷调查情况
D．样本容量是300名学生的问卷调查情况
试题分析：总体是指考查的对象的全体，个体是总体中的每一个考查的对象，样本是总体中所抽取的一部分个体，而样本容量则是指样本中个体的数目．
答案详解：解：A．这是一次抽样调查，故本选项不符合题意；
B．总体是全国各地的青少年生观看“天宫课堂”的情况，故本选项不符合题意；
C．个体是每名学生的问卷调查情况，说法正确，故本选项符合题意；
D．样本容量是300，故本选项不符合题意．
所以选：C．
3．（3分）分式a−xa+x，x−yx2−y2，a+ba2+2ab+b2，a2+b2a+b中最简分式的个数为（ ）
A．1B．2C．3D．4
试题分析：根据最简分式的定义分别对每个分式进行分析即可．
答案详解：解：x−yx2−y2=x−y(x+y)(x−y)=1x+y，a+ba2+2ab+b2=a+b(a+b)2=1a+b，
a−xa+x，a2+b2a+b，是最简分式．
所以选：B．
4．（3分）下列事件属于必然事件的是（ ）
A．367人中至少有两人的生日相同
B．某种彩票的中奖率为1100，购买1000张彩票一定中奖
C．掷一次骰子，向上的一面是6点
D．某射击运动员射击一次，命中靶心
试题分析：根据必然事件的概念（必然事件指在一定条件下一定发生的事件）可判断正确答案．
答案详解：解：A、一年最多有366天，367人中至少有两人的生日相同，是必然事件；
B、某种彩票的中奖率为 1100，购买100张彩票一定中奖，是随机事件；
C、掷一次骰子，向上的一面是6点，是随机事件；
D、某射击运动员射击一次，命中靶心，是随机事件．
所以选：A．
5．（3分）下列二次根式中，与3能合并的是（ ）
A．24B．32C．54D．34
试题分析：各式化简后，利用同类二次根式定义判断即可．
答案详解：解：A、原式＝26，不符合题意；
B、原式＝42，不符合题意；
C、原式＝36，不符合题意；
D、原式=32，符合题意．
所以选：D．
6．（3分）若分式x2−4x+2的值为零，则x的值为（ ）
A．x＝±2B．x＝2C．x＝﹣2D．x＝±4
试题分析：根据分式值为零的条件可得x2﹣4＝0，且x+2≠0，再解即可．
答案详解：解：根据题意得：
x2−4=0x+2≠0，
解得：x＝2．
所以答案是：B．
7．（3分）如图，△MON的顶点M在第一象限，顶点N在x轴上，反比例函数y=kx的图象经过点M，若MO＝MN，△MON的面积为8，则k的值为（ ）
A．4B．8C．﹣৪D．16
试题分析：过M作MA⊥ON于A，根据等腰三角形的性质求出OA＝AN＝a，根据三角形的面积求出ab＝8，即可求出k＝ab＝8．
答案详解：解：过M作MA⊥ON于A，
∵OM＝MN，
∴OA＝AN，
设M点的坐标为（a，b），
则OA＝AN＝a，AM＝b，
∵△MON的面积为8，
∴12×2a×b=8，
∴ab＝8，
∵M在反比例函数y=kx上，
∴ab＝k，
即k＝8，
所以选：B．
8．（3分）如图所示，P是正方形ABCD内一点，△ABP经过旋转后到达△CBQ的位置，连接PQ，则∠BQP的度数为（ ）
A．90°B．60°C．45°D．30°
试题分析：由旋转的性质可得BP＝BQ，∠ABC＝∠PBQ＝90°，由等腰三角形的性质可得∠BQP＝45°．
答案详解：解：∵△ABP经过旋转后到达△CBQ的位置，
∴BP＝BQ，∠ABC＝∠PBQ＝90°，
∴∠BQP＝45°，
所以选：C．
9．（3分）如图，边长为1的正方形ABCD绕点A逆时针旋转60°得到正方形AEFG，连接CF，则CF的长是（ ）
A．1B．2C．3D．32−3
试题分析：连接AC、AF，证明△ACF为等边三角形，求得AC便可得出结果．
答案详解：解：连接AC、AF，
由旋转性质得，AC＝AF，∠CAF＝60°，
∴△ACF为等边三角形，
∴AC＝CF，
∵AC=2AB=2，
∴CF=2，
所以选：B．
二．填空题（共9小题，满分27分，每小题3分）
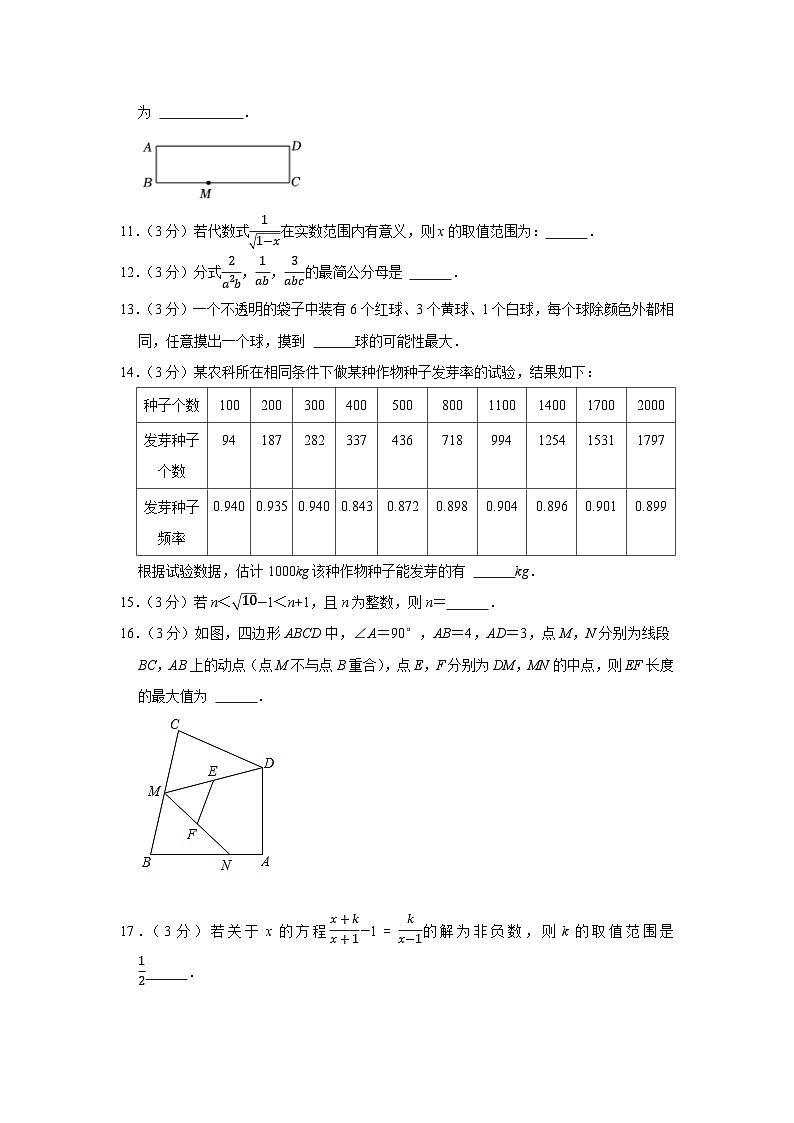
10．（3分）如图，在矩形ABCD中，AB＝3，BC＝15，M为BC的三等分点（BM=13BC），N是从B出发，以每秒1个单位的速度沿B﹣A﹣D方向运动的动点，点N运动t秒后沿MN所在直线，将矩形纸片进行翻折，若点B恰好落在边AD上，则t的值为 53或7 ．
试题分析：分两种情况进行讨论：①点N在AB上；②点N在AD上，结合折叠的性质，可得直角三角形，再利用勾股定理即可求解．
答案详解：解：①如图，过点M作ME⊥AD交AD于点E，N在AB上，
可得四边形ABME是矩形，
∴EM＝AB＝3，AE＝BM，
∵M是BC的三等分点，BC＝15，
∴由折叠性质得B'M＝BM=13BC＝5，
在Rt△B'EM中，B'E=B'M2−EM2=52−32=4，
∴AB'＝AE﹣B'E＝1，
设AN＝x，则NB＝AB﹣AN＝3﹣x，
在Rt△ANB中，AN2+AB2＝x2+12＝NB2＝（3﹣x）2，
解得：x=43，
∴NB＝AB﹣AN=53，
即t=53；
②如图，过点M作ME⊥AD交AD于点E，N在AD上，
可得四边形ABME是矩形，
∴ME＝AB＝3，AE＝BM＝5，
在Rt△EMB'中，B'E=B'M2−EM2=4，
AB'＝AE+B'E＝9，
设AN＝y，则EN＝AE﹣AN＝5﹣y，
∴NB'＝AB'﹣AN＝9﹣y，
在Rt△A'NB'中，NA'2+A'B'2＝y2+32＝NB'2＝（9﹣y）2，
解得：y＝4，即AN＝4，
∴t＝（3+4）÷1＝7．
综上所述，t=53或7．
所以答案是：53或7．
11．（3分）若代数式11−x在实数范围内有意义，则x的取值范围为： x＜1 ．
试题分析：要使代数式有意义，令被开方数≥0，分母≠0，得1﹣x＞0，即可得答案．
答案详解：解：由题意知：1﹣x＞0，
解得：x＜1，
所以答案是：x＜1．
12．（3分）分式2a2b，1ab，3abc的最简公分母是 a2bc ．
试题分析：根据取各分母系数的最小公倍数与字母因式的最高次幂的积作公分母，这样的公分母叫做最简公分母可得答案．
答案详解：解：分式2a2b，1ab，3abc的最简公分母是a2bc．
所以答案是：a2bc．
13．（3分）一个不透明的袋子中装有6个红球、3个黄球、1个白球，每个球除颜色外都相同，任意摸出一个球，摸到 红 球的可能性最大．
试题分析：根据概率公式先求出红球、白球和黄球的概率，再进行比较即可得出答案．
答案详解：解：∵不透明的袋子中装有6个红球、3个黄球、1个白球，
∴袋子中一共有球6+3+1＝10（个），
∴从袋子中任意摸出一个球，摸到红球的概率是：610=35，摸到黄球的概率是310，摸到白球的概率是110，
∴摸到红球的可能性最大．
所以答案是：红．
14．（3分）某农科所在相同条件下做某种作物种子发芽率的试验，结果如下：
根据试验数据，估计1000kg该种作物种子能发芽的有 900 kg．
试题分析：大量重复试验下“发芽种子”的频率可以估计“发芽种子”的概率，据此求解．
答案详解：解：观察表格发现随着实验次数的增多频率逐渐稳定在0.9附近，
故“发芽种子”的概率估计值为0.9，
所以1000kg该种作物种子能发芽的有1000×0.9＝900kg．
所以答案是：900．
15．（3分）若n＜10−1＜n+1，且n为整数，则n＝ 2 ．
试题分析：先找到10在哪两个有理数之间，然后判断出所求的无理数的范围．
答案详解：解：∵3＜10＜4，
∴2＜10−1＜3，
∴n＝2．
所以答案是：2．
16．（3分）如图，四边形ABCD中，∠A＝90°，AB＝4，AD＝3，点M，N分别为线段BC，AB上的动点（点M不与点B重合），点E，F分别为DM，MN的中点，则EF长度的最大值为 2.5 ．
试题分析：连接DN、DB，根据勾股定理求出BD，根据三角形中位线定理得到EF=12DN，结合图形解答即可．
答案详解：解：连接DN、DB，
在Rt△DAB中，∠A＝90°，AB＝4，AD＝3，
∴BD=AD2+AB2=32+42=5，
∵点E，F分别为DM，MN的中点，
∴EF=12DN，
由题意得，当点N与点B重合是DN最大，最大值为5，
∴EF长度的最大值为2.5，
所以答案是：2.5．
17．（3分）若关于x的方程x+kx+1−1=kx−1的解为非负数，则k的取值范围是 k≤12且k≠0 ．
试题分析：首先解分式方程用含k的式子表示x，再根据解是非负数即可求得结果．
答案详解：解：方程x+kx+1−1=kx−1，
（x+k）（x﹣1）﹣（x+1）（x﹣1）＝k（x+1）
x2﹣x+kx﹣k﹣x2+1＝kx+k
x＝﹣2k+1
∵x≥0且x≠1，
∴﹣2k+1≥0且﹣2k+1≠1
解得k≤12且k≠0．
所以答案是k≤12且k≠0．
18．（3分）如图，点A是反比例函数y=6x（x＞0）上的一点，过点A作AC⊥y轴，垂足为点C，AC交反比例函数y=2x的图象于点B，点P是x轴上的动点，则△PAB的面积为 2 ．
试题分析：连接OA、OB、PC，由于AC⊥y轴，根据三角形的面积公式以及反比例函数比例系数k的几何意义得到S△APC＝S△AOC＝3，S△BPC＝S△BOC＝1，然后利用S△PAB＝S△APC﹣S△APB进行计算．
答案详解：解：如图，连接OA、OB、PC，
∵AC⊥y轴，
∴S△APC＝S△AOC=12×|6|＝3，S△BPC＝S△BOC=12×|2|＝1，
∴S△PAB＝S△APC﹣S△APB＝2，
所以答案是：2．
三．解答题（共10小题，满分96分）
19．（8分）计算：
（1）48÷3−12×12+24；
（2）解方程：x+2x−2−4x2−4=1．
试题分析：（1）根据二次根式的乘除法则运算；
（2）先把方程化为整式方程得（x+2）2﹣4＝（x+2）（x﹣2），然后解整式方程后进行检验确定原方程的解．
答案详解：解：（1）原式=48÷3−12×12+26
＝4−6+26
＝4+6；
（2）去分母得（x+2）2﹣4＝（x+2）（x﹣2），
解得x＝﹣1，
检验：当x＝﹣1时，（x+2）（x﹣2）≠0，
所以原方程的解为x＝﹣1．
20．（10分）先化简：（a+7a−1−2a+1）÷a2+3aa2−1，再从﹣3、﹣2、﹣1、0、1中选一个合适的数作为a的值代入求值．
试题分析：原式括号中两项通分并利用同分母分式的减法法则计算，同时利用除法法则变形，约分得到最简结果，把a的值代入计算即可求出值．
答案详解：解：原式=(a+7)(a+1)−2(a−1)(a+1)(a−1)•(a+1)(a−1)a(a+3)
=a2+6a+9a(a+3)
=(a+3)2a(a+3)
=a+3a，
当a＝﹣3，﹣1，0，1时，原式没有意义，舍去，
当a＝﹣2时，原式=−12．
21．（8分）某市教育部门为了了解初中数学课堂中学生参与情况，并按“主动质疑、独立思考、专注听讲、讲解题目”四个项目进行评价．调研小组随机抽查部分学校若干名学生，并将抽查学生的课堂参与情况绘制成如下两幅均不完整的统计图．请根据统计图中的信息解答下列问题：
（1）本次抽查的学生人数是 560 ；
（2）在扇形统计图中，“主动质疑”对应的圆心角度数为 54° ；
（3）将条形统计图补充完整；
（4）若该市初中生共有80000名，则在课堂中能“独立思考”的学生约有多少人？
试题分析：（1）根据专注听讲的人数是224人，所占的比例是40%，即可求得抽查的总人数；
（2）利用360°乘以对应的百分比即可求解；
（3）利用总人数减去其他各组的人数，即可求得讲解题目的人数，从而补全条形统计图即可；
（4）利用80000乘以对应的比例即可．
答案详解：解：（1）本次调查的样本容量为224÷40%＝560（人），
所以答案是：560；
（2）“主动质疑”所在的扇形的圆心角的度数是：360°×84560=54°，
所以答案是：54°；
（3）“讲解题目”的人数是：560﹣84﹣168﹣224＝84（人）．
补全条形统计图如图：
（4）80000×168560=24000（人），
答：在课堂上能独立思考的学生约有24000人．
22．（8分）一个不透明的袋子里装有黑白两种颜色的球若干个，这些球除颜色外都相同．从袋子中随机摸一个球，记下颜色后放回搅匀，不断重复上面的过程，并绘制了如图所示的统计图，根据统计图提供的信息解决下列问题：
（1）摸到白球的概率估计值为 0.2 （精确到0.1）；
（2）若袋子中白球有4个，
①求袋中黑色球的个数；
②若将m个相同的白球放进了这个不透明的袋子里，然后再次进行摸球试验，当大量重复试验后，摸出白球的概率估计值是 4+m20+m ．（用含m的式子表示）
试题分析：（1）根据图象可以看出，摸到白球的频率在0.2左右附近摆动．根据频率与概率的关系，可知摸到白球的概率约为0.2．
（2）①根据摸到白球的频率与白球的个数可得袋中球的总个数，则根据黑球个数＝袋中球的总个数﹣白球的个数求之即可．
②根据摸出白球的频率＝白球的个数÷球的总个数，然后根据频率与概率的关系，估计出摸出白球的概率．
答案详解：解：（1）由题图可以看出，随着摸球次数的增多，摸到白球的频率在0.20左右摆动．
根据频率与概率的关系，可知摸到白球的概率为0.2．
所以答案是：0.2．
（2）①∵袋子中白球有4个．
∴袋中球的总个数为4÷0.2＝20．
∴袋中黑色球的个数为20﹣4＝16．
②∵将m个相同的白球放进了这个不透明的袋子里．
∴袋中白球的个数为4+m，袋中球的总个数为20+m．
∴摸到白球的频率为4+m20+m．
根据频率与概率的关系可得，
摸到白球的概率为4+m20+m．
所以答案是：4+m20+m．
23．（10分）2020年初，为应对突如其来的“新冠肺炎”，某药店用3000元购进了第一批口罩，上市后很快售完，接着又用9000元购进第二批口罩，已知第二批所购口罩的进价比第一批每盒多20元，且数量是第一批的1.5倍．问第二批口罩每盒的进价是多少元？
试题分析：设第一批口罩每盒的进价是x元，则第二批口罩每盒的进价是（x+20）元，根据数量＝总价÷单价结合第二批所购口罩的数量是第一批所购口罩数的1.5倍，即可得出关于x的分式方程，解之经检验后即可得出结论．
答案详解：解：设第一批口罩每盒的进价是x元，则第二批口罩每盒的进价是（x+20）元，
依题意，得：9000x+20=1.5×3000x，
解得：x＝20，
经检验，x＝20是原方程的解，且符合题意．
所以x+20＝40．
答：第二批口罩每盒的进价是40元．
24．（10分）如图，在▱ABCD中，F是边DC的中点，过点F作FE∥AD，交AB于点E．连接ED、EC，作CG∥DE，交EF的延长线于点G，连接DG．
（1）求证：四边形DECG是平行四边形；
（2）当DE平分∠ADC时，求证：四边形DECG是矩形．
试题分析：（1）先证△DEF≌△CGF（AAS），得DE＝CG，再由CG∥DE，即可得出结论；
（2）证∠DEF＝∠EDF，得EF＝DF，再证CD＝EG，即可得出结论．
答案详解：证明：（1）∵F是边DC的中点，
∴DF＝CF．
∵CG∥DE，
∴∠DEF＝∠CGF．
又∵∠DFE＝∠CFG，
∴△DEF≌△CGF（AAS），
∴DE＝CG，
∵CG∥DE，
∴四边形DECG是平行四边形．
（2）∵ED平分∠ADC，
∴∠ADE＝∠FDE．
∵EF∥AD，
∴∠ADE＝∠DEF．
∴∠DEF＝∠EDF，
∴EF＝DF，
∵DF＝CF，
∴CD＝EG，
又∵四边形DECG是平行四边形，
∴平行四边形DECG是矩形．
25．（8分）已知关于x的一元二次方程（m﹣1）x2﹣（m+1）x+2＝0有实数根．
（1）求m的取值范围；
（2）若方程的两个实数根均为正整数，求整数m的值．
试题分析：（1）利用一元二次方程的定义和根的判别式得到m﹣1≠0且Δ＝（m+1）2﹣4×（m﹣1）×2＝（m﹣3）2≥0，然后求出两不等式的公共部分即可；
（2）利用求根公式解方程得到得x1＝1，x2=2m−1，然后利用有理数整除性求m的值．
答案详解：解：（1）根据题意得m﹣1≠0且Δ＝（m+1）2﹣4×（m﹣1）×2＝（m﹣3）2≥0，
解得m≠1；
（2）x=m+1±(m−3)2(m−1)，
解得x1＝1，x2=2m−1，
∵方程的两个实数根均为正整数，m为整数，
∴m﹣1＝1或m﹣1＝2，
∴m＝2或m＝3．
26．（8分）我们知道菱形与正方形的形状有差异，可以将菱形与正方形的接近程度称为菱形的“接近度”．如图，已知菱形ABCD的边长为5，设菱形ABCD的对角线BD，AC的长分别为m，n（m≥n）．若我们将菱形的“接近度”定义为mn，即“接近度”=mn．
（1）当菱形的“接近度”＝ 1 时，菱形就是正方形；
（2）在菱形ABCD中，∠ABC＝60°，求此菱形的“接近度”；
（3）若菱形ABCD的“接近度”是2，求此时菱形ABCD面积．
试题分析：（1）根据当菱形的“接近度”等于1时，菱形ABCD的对角线BD，AC的长相等，进而得出答案；
（2）利用菱形性质可得△ABC是等边三角形，进而可以解决问题；
（3）根据当菱形的“接近度”等于2，菱形ABCD的边长为5，可得菱形对角线长，进而得出答案．
答案详解：解：（1）当菱形的“接近度”＝1时，菱形的对角线相等，此时菱形就是正方形；
所以答案是：1；
（2）在菱形ABCD中，∠ABC＝60°，
∴△ABC是等边三角形，
∴该菱形形ABCD的“接近度”等于3；
（3）若菱形ABCD的“接近度”是2，
∵菱形ABCD的边长为5，
∴菱形ABCD的对角线BD，AC的长分别为45，25，
此时菱形ABCD面积=12×45×25=20．
27．（12分）如图，在平面直角坐标系xOy中，直线y＝2x+2与函数y=kx（k≠0）的图象交于A，B两点，且点A的坐标为（1，m），点B的坐标为（n，﹣2）．
（1）求k，m，n的值；
（2）直接写出关于x的不等式2x+2＞kx的解集；
（3）若Q在x轴上，△ABQ的面积是6，求Q点坐标．
试题分析：（1）将点A坐标代入直线解析式可求m的值，再将点A坐标代入反比例函数解析式可求k的值；
（2）由（1）知A、B的坐标，然后根据函数的图象即可求得不等式2x+2＞kx的解集．
（3）由直线解析式求得直线与x轴的交点坐标，然后设出Q的坐标，根据三角形面积公式得到12•|a+1|•（2+4）＝6，解得a的值，即可求得点Q的坐标．
答案详解：解：（1）将A（1，m）代入y＝2x+2中得：
m＝2+2＝4，
∴A（1，4），
再将A（1，4）代入函数y=kx（k≠0）中，
k＝4，
将B（n，﹣2）代入y＝2x+2中得：
n＝﹣2，
综上，k＝4，m＝4，n＝﹣2；
（2）由（1）得：A（1，4），B（﹣2，﹣2），
由图象易知：﹣2＜x＜0或x＞1；
（3）在y＝2x+2中令y＝0，解得x＝﹣1，
则直线与x轴的交点是（﹣1，0），
设点Q的坐标是（a，0），如图所示：
∵△ABQ的面积是6，
∴12•|a+1|•（2+4）＝6，则|a+1|＝2，
解得：a＝1或﹣3，
则点Q的坐标是（﹣3，0）或（1，0）．
28．（14分）在正方形ABCD中，点E，F在对角线AC上，AC＝12．
（1）如图（1），若BE＝BF，则AE与CF相等吗？请说明理由；
（2）如图（2），若∠EBF＝45°，CF＝4，求EF的长；
（3）如图（3），若点E，F是AC的三等分点，点P在正方形ABCD的边上从点A开始按逆时针方向运动一周，直至返回点A，试求此过程中满足PE+PF为整数的点P个数．
试题分析：（1）连接BD，利用正方形的性质和等腰三角形的性质和等式的性质解答即可；
（2）将△BCF绕着点B逆时针旋转90°得到△BAG，连接EG，利用旋转的性质和全等三角形的判定与性质和勾股定理解答即可；
（3）先求得点P在边AB上运动时，PE+PF为整数时的P的个数，再利用对称性即可得出结论．
答案详解：解：（1）AE＝CF，理由：
连接BD，如图，
∵四边形ABCD是正方形，
∴AC⊥BD，OA＝OC．
∵BE＝BF，
∴OE＝OF，
∴OA﹣OE＝OC﹣OF．
即：AE＝BF．
（2）将△BCF绕着点B逆时针旋转90°得到△BAG，连接EG，如图，
则△BCF≌△BGA，
∴∠ABG＝∠FBC，∠GAB＝∠FCB＝45°，BG＝BF，
∴∠GAE＝∠GAB+∠BAC＝45°+45°＝90°，
∵∠ABC＝90°，∠EBF＝45°，
∴∠ABE+∠CBF＝45°，
∴∠GBA+∠ABE＝45°，
即：∠GBE＝45°，
∴∠GBE＝∠FBE＝45°．
在△GBE和△FBE中，
BG=BF∠GBE=∠FBEBE=BE，
∴△GBE和△FBE（SAS），
∴GE＝EF，AG＝CF＝4．
设EF＝BG＝x，则AE＝AC﹣CF﹣EF＝8﹣x，
在Rt△AGE中，
∵AG2+AE2＝GE2，
∴42+（8﹣x）2＝x2，
解得：x＝5，
∴EF＝5；
（3）当P，A两点重合时，PE+PF＝4+8＝12，符合题意；
当点P在A，B两点之间时，
作点E关于AB的对称点E′，连接E′F交AB于点P，如图，
则此时PE+PF的值最小，
∵点E关于AB的对称点E′，
∴AE′＝AE＝4，PE′＝PE，AB⊥E′E，
∴∠E′AB＝∠EAB＝45°，
∴∠E′AE＝90°，
∴PE+PF＝PE′+PF＝E′F=AE'2+AF2=45＜9；
当P，B两点重合时，连接BD交AC于点O，如图，
则OE＝OA﹣AE＝2，OB＝OA＝6，
∴PE＝BE=OB2+OE2=210，
同理，PF＝210，
∴PE+PF＝410＜13，不符合题意，
∴点P在AB边上运动时，45≤PE+PF≤410，则符合题意的点有8个（包括点A），
由对称性可知，在正方形的四边上符合题意的点有：7×4+2＝30．种子个数
100
200
300
400
500
800
1100
1400
1700
2000
发芽种子个数
94
187
282
337
436
718
994
1254
1531
1797
发芽种子频率
0.940
0.935
0.940
0.843
0.872
0.898
0.904
0.896
0.901
0.899