【真题汇总卷】湖南省邵阳市中考数学真题模拟测评 （A）卷（含答案及解析）

这是一份【真题汇总卷】湖南省邵阳市中考数学真题模拟测评 （A）卷（含答案及解析），共31页。试卷主要包含了有理数 m等内容，欢迎下载使用。
考生注意：
1、本卷分第I卷（选择题）和第Ⅱ卷（非选择题）两部分，满分100分，考试时间90分钟
2、答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上
3、答案必须写在试卷各个题目指定区域内相应的位置，如需改动，先划掉原来的答案，然后再写上新的答案；不准使用涂改液、胶带纸、修正带，不按以上要求作答的答案无效。
第I卷（选择题 30分）
一、单选题（10小题，每小题3分，共计30分）
1、下列式子中，与是同类项的是（ ）
A．abB．C．D．
2、如图，点A，B，C在⊙O上，∠ACB=35°，则∠AOB的度数是（ ）
A．75°B．70°C．65°D．55°
3、下列语句中，不正确的是（ ）
A．0是单项式B．多项式的次数是4
C．的系数是D．的系数和次数都是1
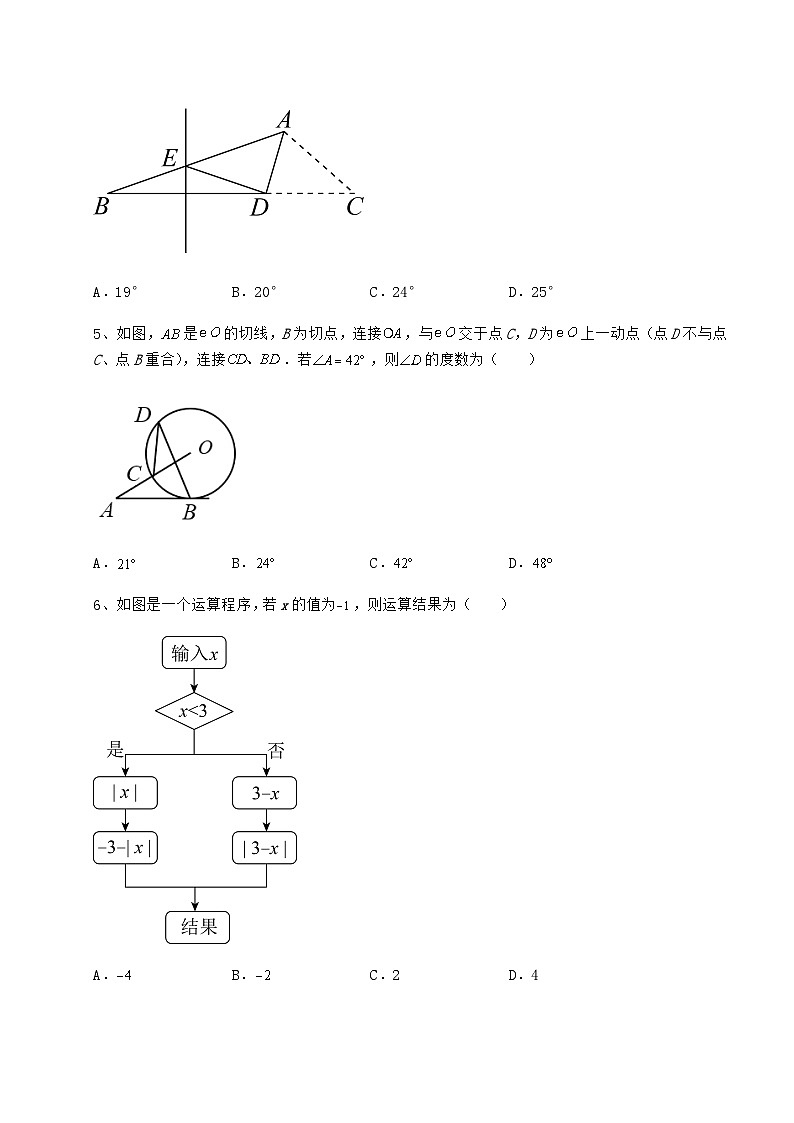
4、如图，在中，，点D是BC上一点，BD的垂直平分线交AB于点E，将沿AD折叠，点C恰好与点E重合，则等于（ ）
A．19°B．20°C．24°D．25°
5、如图，是的切线，B为切点，连接，与交于点C，D为上一动点（点D不与点C、点B重合），连接．若，则的度数为（ ）
A．B．C．D．
6、如图是一个运算程序，若x的值为，则运算结果为（ ）
A．B．C．2D．4
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 内 · · · · · · ○ · · · · · ·
号学级年名姓
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 外 · · · · · · ○ · · · · · ·
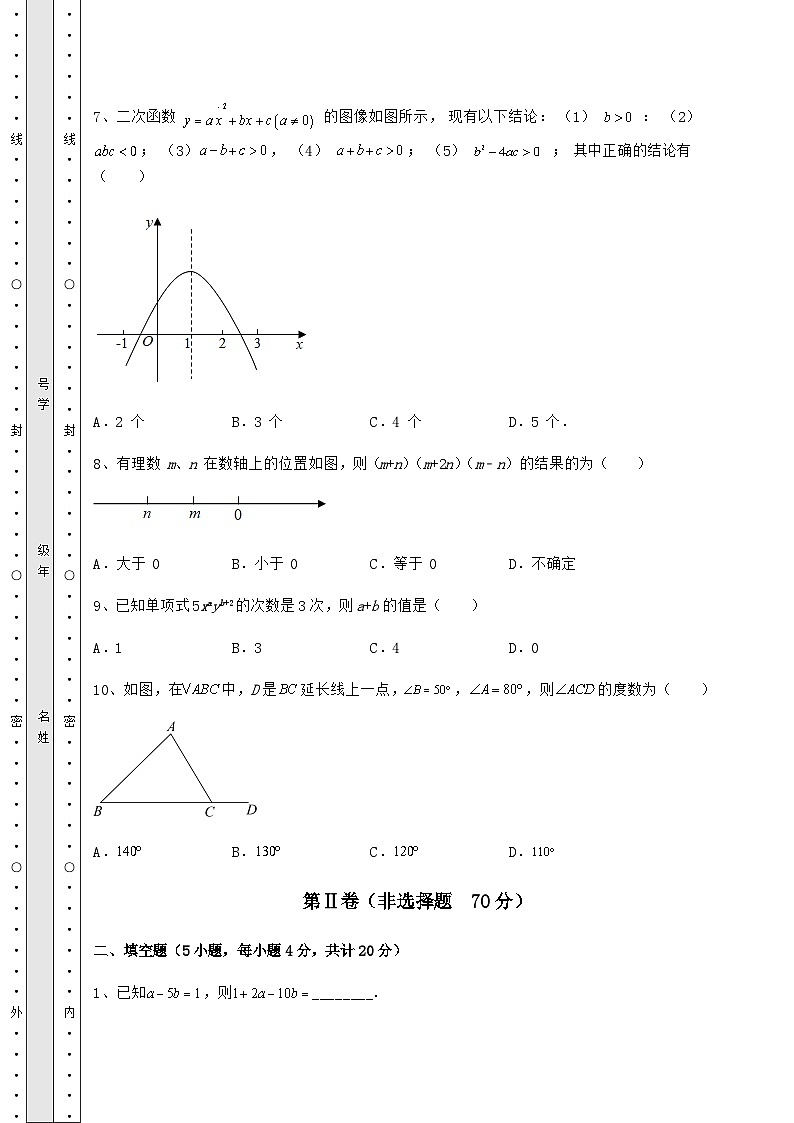
7、二次函数 的图像如图所示， 现有以下结论： （1） ： （2） ； （3）， （4） ； （5） ； 其中正确的结论有（ ）
A．2 个B．3 个C．4 个D．5 个．
8、有理数 m、n 在数轴上的位置如图，则（m+n）（m+2n）（m﹣n）的结果的为（ ）
A．大于 0B．小于 0C．等于 0D．不确定
9、已知单项式5xayb+2的次数是3次，则a+b的值是（ ）
A．1B．3C．4D．0
10、如图，在中，D是延长线上一点，，，则的度数为（ ）
A．B．C．D．
第Ⅱ卷（非选择题 70分）
二、填空题（5小题，每小题4分，共计20分）
1、已知，则________．
2、在平行四边形ABCD中，对角线AC长为8cm，，，则它的面积为______cm2．
3、计算：______．
4、若过某多边形一个顶点的所有对角线将这个多边形分成3个三角形，则这个多边形是________边形．
5、如图是两个全等的三角形，图中字母表示三角形的边长，则∠的度数为________º.
三、解答题（5小题，每小题10分，共计50分）
1、解方程：．
2、如图，一次函数的图象与反比例函数的图象相交于和两点．
（1）______，_______；
（2）结合图象直接写出不等式的解集．
3、如图，在中，，将绕点C旋转得到，连接AD．
（1）如图1，点E恰好落在线段AB上．
①求证：；
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 内 · · · · · · ○ · · · · · ·
号学级年名姓
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 外 · · · · · · ○ · · · · · ·
②猜想和的关系，并说明理由；
（2）如图2，在旋转过程中，射线BE交线段AC于点F，若，，求CF的长．
4、（1）如图1，四边形ABCD是矩形，以对角线AC为直角边作等腰直角三角形EAC，且．请证明：；
（2）图2，在矩形ABCD中，，，点P是AD上一点，且，连接PC，以PC为直角边作等腰直角三角形EPC，，设，，请求出y与x的函数关系式；
（3）在（2）的条件下，连接BE，若点P在线段AD上运动，在点P的运动过程中，当是等腰三角形时，求AP的长．
5、在等腰中，，，点在直线上．
（1）如图1所示，点在上，点是的中点，连接．若，，求的周长；
（2）如图2所示，点在的延长线上，连接，过点作的垂线交于点．点在上，于点，连接．若，，求证：；
（3）如图3所示，点、在边上，连接、，，点是的中点，连接，与交于点．将沿着翻折，点的对应点是点，连接．若，，请直接写出的面积．
-参考答案-
一、单选题
1、D
【分析】
根据同类项是字母相同，相同字母的指数也相同的两个单项式进行解答即可．
【详解】
解：A、ab与ab2不是同类项，不符合题意；
B、a2b与ab2不是同类项，不符合题意；
C、ab2c与ab2不是同类项，不符合题意；
D、－2ab2与ab2是同类项，符合题意；
故选：D．
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 内 · · · · · · ○ · · · · · ·
号学级年名姓
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 外 · · · · · · ○ · · · · · ·
【点睛】
本题考查同类项，理解同类项的概念是解答的关键．
2、B
【分析】
直接根据圆周角定理求解．
【详解】
解：，
．
故选：B．
【点睛】
本题考查了圆周角定理，解题的关键是掌握在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．
3、D
【分析】
分别根据单独一个数也是单项式、多项式中每个单项式的最高次数是这个多项式的次数、单项式中的数字因数是这个单项式的系数、单项式中所有字母的指数和是这个单项式的次数解答即可．
【详解】
解：A、0是单项式，正确，不符合题意；
B、多项式的次数是4，正确，不符合题意；
C、的系数是，正确，不符合题意；
D、的系数是－1，次数是1，错误，符合题意，
故选：D．
【点睛】
本题考查单项式、单项式的系数和次数、多项式的次数，理解相关知识的概念是解答的关键．
4、B
【分析】
根据垂直平分线和等腰三角形性质，得；根据三角形外角性质，得；根据轴对称的性质，得，，；根据补角的性质计算得，根据三角形内角和的性质列一元一次方程并求解，即可得到答案．
【详解】
∵BD的垂直平分线交AB于点E，
∴
∴
∴
∵将沿AD折叠，点C恰好与点E重合，
∴，，
∵
∴
∵
∴
∴
故选：B．
【点睛】
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 内 · · · · · · ○ · · · · · ·
号学级年名姓
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 外 · · · · · · ○ · · · · · ·
本题考查了轴对称、三角形内角和、三角形外角、补角、一元一次方程的知识；解题的关键是熟练掌握轴对称、三角形内角和、三角形外角的性质，从而完成求解．
5、B
【分析】
如图：连接OB，由切线的性质可得∠OBA=90°，再根据直角三角形两锐角互余求得∠COB，然后再根据圆周角定理解答即可．
【详解】
解：如图：连接OB，
∵是的切线，B为切点
∴∠OBA=90°
∵
∴∠COB=90°-42°=48°
∴=∠COB=24°．
故选B．
【点睛】
本题主要考查了切线的性质、圆周角定理等知识点，掌握圆周角等于对应圆心角的一半成为解答本题的关键．
6、A
【分析】
根据运算程序，根据绝对值的性质计算即可得答案．
【详解】
∵＜3，
∴=，
故选：A．
【点睛】
本题考查绝对值的性质及有理数的加减运算，熟练掌握绝对值的性质及运算法则是解题关键．
7、C
【分析】
由抛物线的开口方向判断a与0的关系，由抛物线与y轴的交点判断c与0的关系，然后根据对称轴及抛物线与x轴交点情况进行推理，进而对所得结论进行判断．
【详解】
解：（1）∵函数开口向下，∴a＜0，∵对称轴在y轴的右边，∴，∴b＞0，故命题正确；
（2）∵a＜0，b＞0，c＞0，∴abc＜0，故命题正确；
（3）∵当x=-1时，y＜0，∴a-b+c＜0，故命题错误；
（4）∵当x=1时，y>0，∴a+b+c>0，故命题正确；
（5）∵抛物线与x轴于两个交点，∴b2-4ac＞0，故命题正确；
故选C．
【点睛】
本题考查了二次函数图象与二次函数系数之间的关系，会利用对称轴的范围求2a与b的关系，以及二次函数与方程之间的转换，根的判别式的熟练运用．
8、A
【分析】
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 内 · · · · · · ○ · · · · · ·
号学级年名姓
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 外 · · · · · · ○ · · · · · ·
从数轴上看出，判断出，进而判断的正负．
【详解】
解：由题意知：
∴
∴
故选A．
【点睛】
本题考查了有理数加减的代数式正负的判断．解题的关键在于正确判断各代数式的正负．
9、A
【分析】
根据单项式的次数的概念求解．
【详解】
解：由题意得：a+b+2=3，
∴a+b=1．
故选：A．
【点睛】
本题考查了单项式的有关概念，解答本题的关键是掌握单项式的次数：所有字母的指数和．
10、B
【分析】
根据三角形外角的性质可直接进行求解．
【详解】
解：∵，，
∴；
故选B．
【点睛】
本题主要考查三角形外角的性质，熟练掌握三角形外角的性质是解题的关键．
二、填空题
1、3
【解析】
【分析】
把变形后把代入计算即可．
【详解】
解：∵，
∴，
故答案为：3．
【点睛】
此题主要考查了代数式求值问题，要熟练掌握，求代数式的值可以直接代入、计算，也可以运用整体代入的思想，本题就利用了整体代入进行计算．
2、20
【解析】
【分析】
根据S▱ABCD=2S△ABC，所以求S△ABC可得解．作BE⊥AC于E，在直角三角形ABE中求BE从而计算S△ABC．
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 内 · · · · · · ○ · · · · · ·
号学级年名姓
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 外 · · · · · · ○ · · · · · ·
【详解】
解：如图，过B作BE⊥AC于E．
在直角三角形ABE中，
∠BAC=30°，AB=5，
∴BE=AB=，
S△ABC=AC•BE=10，
∴S▱ABCD=2S△ABC=20(cm2)．
故答案为：20．
【点睛】
本题综合考查了平行四边形的性质，含30度的直角三角形的性质等．先求出对角线分成的两个三角形中其中一个的面积，然后再求平行四边形的面积，这样问题就比较简单了．
3、-1
【解析】
【分析】
根据有理数减法法则计算即可．
【详解】
解：，
故答案为：-1．
【点睛】
本题考查了有理数减法，解题关键是熟记有理数减法法则，准确计算．
4、五
【解析】
【分析】
根据过多边形的一个顶点的所有对角线，将这个多边形分成(n-2)个三角形，计算可求解．
【详解】
解：设这是个n边形，由题意得
n-2=3，
∴n=5，
故答案为：五．
【点睛】
本题主要考查多边形的对角线，掌握多边形对角线的性质是解题的关键．
5、70
【解析】
【分析】
如图（见解析），先根据三角形的内角和定理可得，再根据全等三角形的性质即可得．
【详解】
解：如图，由三角形的内角和定理得：，
图中的两个三角形是全等三角形，在它们中，边长为和的两边的夹角分别为和，
，
故答案为：70．
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 内 · · · · · · ○ · · · · · ·
号学级年名姓
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 外 · · · · · · ○ · · · · · ·
【点睛】
本题考查了三角形的内角和定理、全等三角形的性质，熟练掌握全等三角形的性质是解题关键．
三、解答题
1、
【分析】
去分母，移项合并同类项，系数化为1即可求解．
【详解】
．
去分母得：．
去括号得：
移项合并同类项得：．
系数化为1得：．
【点睛】
本题考查一元一次方程的解法，先去分母、移项合并、化系数为1．属于基础题．
2、
（1），
（2）或
【分析】
（1）把A（-1，m），B（n，-1）分别代入反比例函数解析式可求出m、n；
（2）确定A点坐标为（-1，2），B点坐标为（2，-1），然后根据图象即可求得．
（1）
把A（-1，m），B（n，-1）分别代入得-m=-2，-n=-2，
解得m=2，n=2，
故答案为：2，2
（2）
∵m=2，n=2，
∴A点坐标为（-1，2），B点坐标为（2，-1），
根据图象可得，不等式的解集为或．
【点睛】
本题考查了反比例函数与一次函数的交点问题：反比例函数与一次函数图象的交点坐标满足两函数解析式．也考查了待定系数法求函数解析式．
3、
（1）①见解析；②，理由见解析
（2）3或
【分析】
（1）①由旋转的性质得，，，根据相似的判定定理即可得证；
②由旋转和相似三角形的性质得，由得，故，代换即可得出结果；
（2）设，作于H，射线BE交线段AC于点F，则，由旋转可证，由相似三角形的性质得，即，由此可证，故，求得，分情况讨论：①当线段BE交AC于F时、当射· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 内 · · · · · · ○ · · · · · ·
号学级年名姓
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 外 · · · · · · ○ · · · · · ·
线BE交AC于F时，根据相似比求出x的值，再根据勾股定理即可求出CF的长．
（1）
①∵将绕点C旋转得到，
∴，，，
∴，，
∴；
②，理由如下：
∵将绕点C旋转得到，
∴，
∵，，，
∴，
∵，
∴，
∴，
∴；
（2）
设，作于H，射线BE交线段AC于点F，则，
∵将绕点C旋转得到，
∴，，，
∴，，
∴，
∴，，即，
∵，
∴，
∴，
∵，，
∴
①当线段BE交AC于F时，
解得，（舍），
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 内 · · · · · · ○ · · · · · ·
号学级年名姓
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 外 · · · · · · ○ · · · · · ·
∴，
②当射线BE交AC于F时，
解得（舍），，
∴，
综上，CF的长为3或．
【点睛】
本题考查相似三角形的判定与性质以及旋转的性质，掌握相似三角形的判定定理以及性质是解题的关键．
4、（1）证明见解析；（2）；（3）或
【分析】
（1）根据矩形和勾股定理的性质，得；再根据直角等腰三角形的性质计算，即可完成证明；
（2）根据矩形和勾股定理的性质，得,再根据勾股定理、直角等腰三角形的性质计算，即可得到答案；
（3）过点E作于点F，交AD于点Q，通过证明四边形和四边形是矩形，得，根据等腰直角三角形性质，推导得，通过证明，得，根据题意，等腰三角形分三种情况分析，当时，根据（2）的结论，得：，通过求解一元二次方程，得；当时，根据勾股定理列一元二次方程并求解，推导得不成立，当时，结合矩形的性质，计算得，从而完成求解．
【详解】
（1）∵四边形ABCD是矩形，AC是对角线
∴，
∴
∵以AC为直角边作等腰直角三角形EAC，且
∴；
（2）∵四边形ABCD是矩形，
∴，
∵以PC为直角边作等腰直角三角形EPC，
∴
∴；
（3）过点E作于点F，交AD于点Q，
∴，
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 内 · · · · · · ○ · · · · · ·
号学级年名姓
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 外 · · · · · · ○ · · · · · ·
∵四边形ABCD是矩形
∴，，
∴四边形和四边形是矩形
∴
∵等腰直角三角形EPC，
∴，
∴
∴
在和中

∴，
∴，
∴，，
∴，
①当时，得：，
∴，
解得，
∵，故舍去；
②当时，得：
，
∴
∵
∴无实数解；
③当时
∵
∴
∵，，
∴四边形为矩形
∴
∵，
∴
∴
∴综上所述，或时，是等腰三角形．
【点睛】
本题考查了直角三角形、等腰三角形、勾股定理、矩形、一元二次方程、全等三角形的知识；解题的关键是熟练掌握等腰三角形、勾股定理、一元二次方程的性质，从而完成求解．
5、
（1）
（2）见解析
（3）
【分析】
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 内 · · · · · · ○ · · · · · ·
号学级年名姓
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 外 · · · · · · ○ · · · · · ·
（1）过点作于点，根据，设，则，进而根据等腰直角三角形的性质表示出，根据勾股定理求得，进而求得的值，即可求得的周长；
（2）过点作，垂足为，证明，设交于点，过点作交于，连接，证明四边形，是平行四边形，可得，又,进而即可得证；
（3）过点作，连接,延长交于点，连接，，根据翻折的性质可得，点是的中点，，，可得，根据等底同高，进而证明，即可得则，根据相似三角形的性质以及正弦的定义可得，再根据相似三角形的性质可得，进而即可求得
（1）
如图，过点作于点，
，，
设，则
在中，
是的中点
在中，，，
在中，
的周长为
的周长为
（2）
如图，过点作，垂足为，
在中，，，
，，
在与中
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 内 · · · · · · ○ · · · · · ·
号学级年名姓
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 外 · · · · · · ○ · · · · · ·
设交于点，过点作交于，连接，如图，
是的高，
垂直平分
，
，
又
又
又
四边形是平行四边形
又
四边形是平行四边形
（3）
如图，过点作，连接,延长交于点，连接，，
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 内 · · · · · · ○ · · · · · ·
号学级年名姓
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 外 · · · · · · ○ · · · · · ·
翻折
，，
点是的中点，
，
，
又
设
，
是的中点，
在中，
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 内 · · · · · · ○ · · · · · ·
号学级年名姓
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 外 · · · · · · ○ · · · · · ·
如图，过点作
又是的中点，
又
是的中点，是的中点
,为的中点
设，则,

· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 内 · · · · · · ○ · · · · · ·
号学级年名姓
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 外 · · · · · · ○ · · · · · ·
【点睛】
本题考查了解直角三角形，平行四边形的性质与判定，直角三角形斜边上的中线等于斜边的一半，等腰三角形的性质与判定，轴对称的性质，勾股定理，相似三角形的性质与判定，掌握等腰直角三角形的性质，相似三角形的性质与判定是解题的关键．