真题解析湖南省怀化市中考数学历年真题汇总 （A）卷（含答案及详解）

这是一份真题解析湖南省怀化市中考数学历年真题汇总 （A）卷（含答案及详解），共32页。试卷主要包含了下列函数中，随的增大而减小的是，下列现象，一元二次方程的根为，如图，某汽车离开某城市的距离y等内容，欢迎下载使用。

考生注意：
1、本卷分第I卷（选择题）和第Ⅱ卷（非选择题）两部分，满分100分，考试时间90分钟
2、答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上
3、答案必须写在试卷各个题目指定区域内相应的位置，如需改动，先划掉原来的答案，然后再写上新的答案；不准使用涂改液、胶带纸、修正带，不按以上要求作答的答案无效。
第I卷（选择题 30分）
一、单选题（10小题，每小题3分，共计30分）
1、如图，已知二次函数的图像与x轴交于点，对称轴为直线．结合图象分析下列结论：①；②；③；④一元二次方程的两根分别为；⑤若为方程的两个根，则且．其中正确的结论个数是（ ）
A．2个B．3个C．4个D．5个
2、如图，、是的切线，、是切点，点在上，且，则等于（ ）
A．54°B．58°C．64°D．68°
3、一副三角板按如图所示的方式摆放，则∠1补角的度数为（ ）
A．B．C．D．
4、下列函数中，随的增大而减小的是（ ）
A．B．
C．D．
5、在如图的月历表中，任意框出表中竖列上三个相邻的数，这三个数的和可能是（ ）．
A．28B．54C．65D．75
6、下列现象：
①用两个钉子就可以把木条固定在墙上
②从A地到B地架设电线，总是尽可能沿着线段AB架设
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 内 · · · · · · ○ · · · · · ·
号学级年名姓
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 外 · · · · · · ○ · · · · · ·
③植树时，只要确定两棵树的位置，就能确定同一行树所在的直线
④把弯曲的公路改直，就能缩短路程
其中能用“两点之间线段最短”来解释的现象有（ ）
A．①④B．①③C．②④D．③④
7、如图，点F在BC上，BC=EF，AB=AE，∠B=∠E，则下列角中，和2∠C度数相等的角是（ ）
A．B．C．D．
8、一元二次方程的根为（ ）
A．B．C．D．
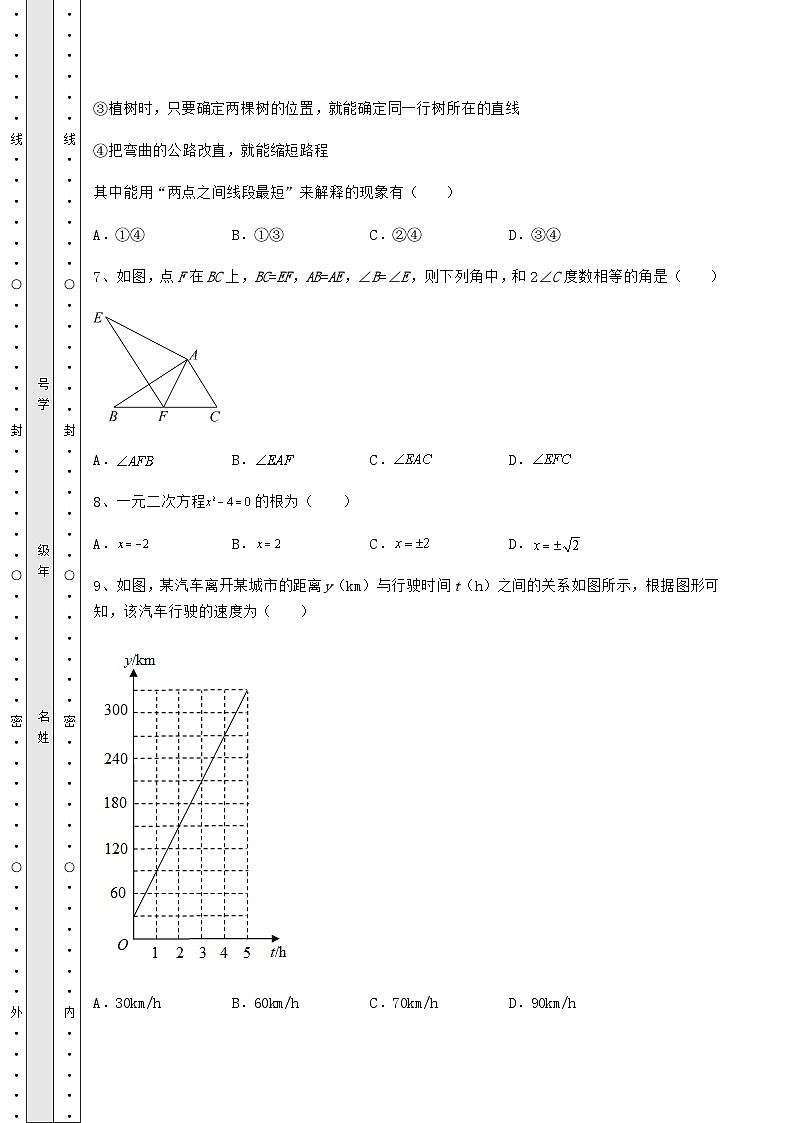
9、如图，某汽车离开某城市的距离y（km）与行驶时间t（h）之间的关系如图所示，根据图形可知，该汽车行驶的速度为（ ）
A．30km/hB．60km/hC．70km/hD．90km/h
10、如图所示，在长方形ABCD中，，，且，将长方形ABCD绕边AB所在的直线旋转一周形成圆柱甲，再将长方形ABCD绕边BC所在直线旋转一周形成圆柱乙，记两个圆柱的侧面积分別为、．下列结论中正确的是（ ）
A．B．C．D．不确定
第Ⅱ卷（非选择题 70分）
二、填空题（5小题，每小题4分，共计20分）
1、在日常生活和生产中有很多现象可以用数学知识进行解释．如图，要把一根挂衣帽的挂钩架水平固定在墙上，至少需要钉______个钉子．用你所学数学知识说明其中的道理______．
2、如图，和均为等边三角形，，分别在边，上，连接，，若，则__________．
3、为调动学生参与体育锻炼的积极性，某校组织了一分钟跳绳比赛活动，体育组随机抽取了10名参赛学生的成绩，将这组数据整理后制成统计表：
则这组数据的众数是______；平均数是______．
4、如图，直角三角形AOB的直角边OA在数轴上，AB与数轴垂直，点O与数轴原点重合，点A表示的实数是2，BA＝2，以点O为圆心，OB的长为半径画弧，与数轴交于点C，则点C对应的数是_____．
5、如图，正方形 边长为 ，则 _____________
三、解答题（5小题，每小题10分，共计50分）
1、一个不透明的口袋中有三个完全相同的小球，把它们分别标号为1，2，3．
（1）随机摸取一个小球的标号是奇数，该事件的概率为_______；
（2）随机摸取一个小球后放回，再随机摸取一个小球．求两次取出的小球标号相同的概率．
2、如图，ABCD，，，试说明：BCDE．请补充说明过程，并在括号内填上相应的理由．
解：∵ABCD（已知），
，
又（已知），
，
，
，
BCDE ．
3、如图，抛物线与x轴相交于点A，与y轴交于点B，C为线段OA上的一个动点，过点C作x轴的垂线，交直线AB于点D，交该抛物线于点E．
（1）求直线AB的表达式，直接写出顶点M的坐标；
（2）当以B，E，D为顶点的三角形与相似时，求点C的坐标；
（3）当时，求与的面积之比．
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 内 · · · · · · ○ · · · · · ·
号学级年名姓
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 外 · · · · · · ○ · · · · · ·
4、在平面直角坐标系xOy中，对于线段AB和点C，若△ABC是以AB为一条直角边，且满足AC>AB的直角三角形，则称点C为线段AB的“关联点”，已知点A的坐标为（0，1）．
（1）若B（2，1），则点D（3，1），E（2，0），F（0，-3），G（-1，-2）中，是AB关联点的有_______；
（2）若点B（-1，0），点P在直线y=2x-3上，且点P为线段AB的关联点，求点P的坐标；
（3）若点B（b，0）为x轴上一动点，在直线y=2x+2上存在两个AB的关联点，求b的取值范围．
5、如图，平面内有两个点A，B．应用量角器、圆规和带刻度的直尺完成下列画图或测量：
（1）经过A，B两点画直线，写出你发现的基本事实；
（2）利用量角器在直线AB一侧画；
（3）在射线BC上用圆规截取BD＝AB（保留作图痕迹）；
（4）连接AD，取AD中点E，连接BE；
（5）通过作图我们知道．，观察并测量图形中的角，写出一组你发现的两个角之间可能存在的数量关系．
-参考答案-
一、单选题
1、C
【分析】
根据图像，确定a，b，c的符号，根据对称轴，确定b，a的关系，当x=-1时，得到a-b+c=0，确定a，c的关系，从而化简一元二次方程，求其根即可，利用平移的思想，把y=的图像向上平移1个单位即可，确定方程的根．
【详解】
∵抛物线开口向上，
∴a＞0，
∵抛物线与y轴的交点在y轴的负半轴上，
∴c＜0，
∵抛物线的对称轴在y轴的右边，
∴b＜0，
∴，
故①正确；
∵二次函数的图像与x轴交于点，
∴a-b+c=0，
根据对称轴的左侧，y随x的增大而减小，
当x=-2时，y＞0即，
故②正确；
∵，
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 内 · · · · · · ○ · · · · · ·
号学级年名姓
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 外 · · · · · · ○ · · · · · ·
∴b= -2a，
∴3a+c=0，
∴2a+c=2a-3a= -a＜0，
故③正确；
根据题意，得，
∴，
解得，
故④错误；
∵=0，
∴，
∴y=向上平移1个单位，得y=+1，
∴为方程的两个根，且且．
故⑤正确；
故选C．
【点睛】
本题考查了抛物线的图像与系数的符号，抛物线的对称性，抛物线与一元二次方程的关系，抛物线的增减性，平移，熟练掌握抛物线的性质，抛物线与一元二次方程的关系是解题的关键．
2、C
【分析】
连接，，根据圆周角定理可得，根据切线性质以及四边形内角和性质，求解即可．
【详解】
解：连接，，如下图：
∴
∵PA、PB是的切线，A、B是切点
∴
∴由四边形的内角和可得：
故选C．
【点睛】
此题考查了圆周角定理，切线的性质以及四边形内角和的性质，解题的关键是熟练掌握相关基本性质．
3、D
【分析】
根据题意得出∠1=15°，再求∠1补角即可．
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 内 · · · · · · ○ · · · · · ·
号学级年名姓
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 外 · · · · · · ○ · · · · · ·
【详解】
由图形可得
∴∠1补角的度数为
故选：D．
【点睛】
本题考查利用三角板求度数和补角的定义，熟记各个三角板的角的度数是解题的关键．
4、C
【分析】
根据各个选项中的函数解析式，可以判断出y随x的增大如何变化，从而可以解答本题．
【详解】
解：A．在中，y随x的增大而增大，故选项A不符合题意；
B．在中，y随x的增大与增大，不合题意；
C．在中，当x＞0时，y随x的增大而减小，符合题意；
D．在，x>2时，y随x的增大而增大，故选项D不符合题意；
故选：C．
【点睛】
本题考查了正比例函数的性质、二次函数的性质、反比例函数的性质，正确掌握相关函数增减性是解题关键．
5、B
【分析】
一竖列上相邻的三个数的关系是：上面的数总是比下面的数小7．可设中间的数是x，则上面的数是x-7，下面的数是x+7．则这三个数的和是3x，让选项等于3x列方程．解方程即可
【详解】
设中间的数是x，则上面的数是x-7，下面的数是x+7，
则这三个数的和是（x-7）+x+（x+7）=3x，
∴3x=28，
解得：不是整数，
故选项A不是；
∴3x=54，
解得： ，
中间的数是18，则上面的数是11，下面的数是28，
故选项B是；
∴3x=65，
解得： 不是整数，
故选项C不是；
∴3x=75，
解得：，
中间的数是25，则上面的数是18，下面的数是32，
日历中没有32，
故选项D不是；
所以这三个数的和可能为54，
故选B．
【点睛】
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 内 · · · · · · ○ · · · · · ·
号学级年名姓
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 外 · · · · · · ○ · · · · · ·
本题考查了一元一次方程的应用，解决的关键是观察图形找出数之间的关系，从而找到三个数的和的特点．
6、C
【分析】
直接利用直线的性质和线段的性质分别判断得出答案．
【详解】
解：①用两个钉子就可以把木条固定在墙上，利用的是两点确定一条直线，故此选项不合题意；
②从A地到B地架设电线，总是尽可能沿着线段AB架设，能用“两点之间，线段最短”来解释，故此选项符合题意；
③植树时，只要确定两棵树的位置，就能确定同一行树所在的直线，利用的是两点确定一条直线，故此选项不合题意；
④把弯曲的公路改直，就能缩短路程，能用“两点之间，线段最短”来解释，故此选项符合题意．
故选：C．
【点睛】
本题考查了直线的性质和线段的性质，正确掌握相关性质是解题关键．
7、D
【分析】
根据SAS证明△AEF≌△ABC，由全等三角形的性质和等腰三角形的性质即可求解．
【详解】
解：在△AEF和△ABC中，
，
∴△AEF≌△ABC（SAS），
∴AF=AC，∠AFE=∠C，
∴∠C=∠AFC，
∴∠EFC=∠AFE+∠AFC=2∠C．
故选：D．
【点睛】
本题主要考查了全等三角形的判定与性质，等腰三角形的判定和性质，熟练掌握全等三角形的判定与性质是解决问题的关键．
8、C
【分析】
先移项，把方程化为 再利用直接开平方的方法解方程即可.
【详解】
解：，

即
故选C
【点睛】
本题考查的是一元二次方程的解法，掌握“利用直接开平方的方法解一元二次方程”是解本题的关键.
9、B
【分析】
直接观察图象可得出结果．
【详解】
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 内 · · · · · · ○ · · · · · ·
号学级年名姓
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 外 · · · · · · ○ · · · · · ·
解：根据函数图象可知：t=1时，y=90；
∵汽车是从距离某城市30km开始行驶的，
∴该汽车行驶的速度为90-30=60km/h，
故选：B．
【点睛】
本题主要考查了一次函数的图象，正确的识别图象是解题的关键．
10、C
【分析】
根据公式，得=，=，判断选择即可．
【详解】
∵=，=，
∴=．
故选C．
【点睛】
本题考查了圆柱体的形成及其侧面积的计算，正确理解侧面积的计算公式是解题的关键．
二、填空题
1、 2 两点确定一条直线
【解析】
【分析】
根据两点确定一条直线解答．
【详解】
解：至少需要钉2个钉子，所学的数学知识为：两点确定一条直线，
故答案为：2，两点确定一条直线．
【点睛】
此题考查了线段的性质：两点确定一条直线，熟记性质是解题的关键．
2、##45度
【解析】
【分析】
根据题意利用全等三角形的判定与性质得出和，进而依据进行计算即可.
【详解】
解：∵和均为等边三角形，
∴，
∴
在和中，
，
∴，
∴，
∴.
故答案为：.
【点睛】
本题考查全等三角形的判定与性质以及等边三角形的性质，熟练掌握全等三角形的判定与性质是解题· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 内 · · · · · · ○ · · · · · ·
号学级年名姓
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 外 · · · · · · ○ · · · · · ·
的关键.
3、 141 143
【解析】
【分析】
根据平均数，众数的性质分别计算出结果即可．
【详解】
解：根据题目给出的数据，可得：
平均数为：＝143；
141出现了5次，出现次数最多，则众数是：141；
故答案为：141；143．
【点睛】
本题考查的是平均数，众数，熟悉相关的计算方法是解题的关键．
4、
【解析】
【分析】
先利用勾股定理求出，再根据作图过程可得，然后根据实数与数轴的关系即可得．
【详解】
解：由题意得：，
，
由作图过程可知，，
由数轴的性质可知，点对应的数大于0，
则在数轴上，点对应的数是，
故答案为：．
【点睛】
本题考查了勾股定理、实数与数轴，掌握理解勾股定理是解题关键．
5、##
【解析】
【分析】
根据正方形的性质可得，过E作EG⊥BC于G，证明三角形EGC是等腰直角三角形，再根据直角三角形BEG利用勾股定理列方程即可．
【详解】
过E作EG⊥BC于G
∵正方形 边长为2
∴，
∵
∴
∴三角形EGC是等腰直角三角形
∴，
在Rt△BEG中，
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 内 · · · · · · ○ · · · · · ·
号学级年名姓
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 外 · · · · · · ○ · · · · · ·
∴
解得：
∴
∴
【点睛】
本题考查正方形的性质及勾股定理，解题的关键是证明三角形EGC是等腰直角三角形，最终根据勾股定理列方程计算即可．
三、解答题
1、
（1）
（2）（两次取出的小球标号相同）
【分析】
（1）直接由概率公式求解即可；
（2）画树状图，共有9种等可能的结果，两次取出小球标号相同的结果有3种，再由概率公式求解即可．
（1）
∵在1，2，3三个数中，其中奇数有1，3共2个数，
∴随机摸取一个小球的标号是奇数，该事件的概率为
故答案为：；
（2）
画树状图如下：
由树状图可知，随机摸取一个小球后放回，再随机摸取一个小球，共有9种等可能的结果，其中两次取出的小球标号相同的结果共有3种，
∴（两次取出的小球标号相同）.
【点睛】
此题考查的是用列表法或树状图法求概率．列表法可以不重复不遗漏的列出所有可能的结果，适合于两步完成的事件；树状图法适合两步或两步以上完成的事件；解题时要注意此题是放回试验还是不放回试验．用到的知识点为：概率=所求情况数与总情况数之比．
2、两直线平行，内错角相等；55；等量代换；已知；；同旁内角互补，两直线平行
【分析】
由题意根据平行线的性质与判定即可补充说理过程．
【详解】
解：（已知），
（两直线平行，内错角相等），
又（已知），
（等量代换），
（已知），
，
（同旁内角互补，两直线平行）．
故答案为：两直线平行，内错角相等；55；等量代换；已知；；同旁内角互补，两直线平行．
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 内 · · · · · · ○ · · · · · ·
号学级年名姓
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 外 · · · · · · ○ · · · · · ·
【点睛】
本题考查平行线的判定与性质，解决本题的关键是掌握平行线的判定与性质．
3、
（1）,，
（2），或，
（3）
【分析】
（1）求出、点的坐标，用待定系数法求直线的解析式即可；
（2）由题意可知是直角三角形，设，分两种情况讨论①当，时，，此时，由此可求；②当时，过点作轴交于点，可证明，则，可求，再由点在抛物线上，则可求，进而求点坐标；
（3）作的垂直平分线交轴于点，连接，过点作于点，则有，在中，，求出，，则，设，则，，则有，求出，即可求．
（1）
解：令，则，
或，
，
令，则，
，
设直线的解析式为，
，
，
，
，
，；
（2）
解：，，
是直角三角形，
设，
①如图1，
当，时，，
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 内 · · · · · · ○ · · · · · ·
号学级年名姓
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 外 · · · · · · ○ · · · · · ·
，
，
（舍或，
，；
②如图2，
当时，
过点作轴交于点，
，，
，
，
，即，
，
，
，
（舍或，
，；
综上所述：点的坐标为，或，；
（3）
解：如图3，作的垂直平分线交轴于点，连接，过点作于点，
，
，
，
，
在中，，
，
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 内 · · · · · · ○ · · · · · ·
号学级年名姓
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 外 · · · · · · ○ · · · · · ·
，
，
，
，
设，则，，
，，，，，
，
，
，
，
．
【点睛】
本题是二次函数的综合题，求一次函数的解析式，解题的关键熟练掌握二次函数的图象及性质，三角形相似的性质与判定，分类讨论，数形结合也是解题的关键．
4、
（1）点E，点F；
（2）（）或（）；
（3）b的取值范围1＜b＜2或2＜b＜3．
【分析】
（1）根据以点B为直角顶点，点B与点E横坐标相同，点E在过点B与AB垂直的直线上，△ABE为直角三角形，且AE大于AB；以点A为直角顶点，点A与点F横坐标相同，△AFB为直角三角形，BF大于AB即可；
（2）根据点A（0，1）点B（-1，0），OA=OB，∠AOB=90°，得出△AOB为等腰直角三角形，可得∠ABO=∠BAO=45°，以点A为直角顶点，过点A，与AB垂直的直线交x轴于S，利用待定系数法求出AS解析式为，联立方程组，以点B为直角顶点，过点B，与AB垂直的直线交y轴于R，∠OBR=90°-∠ABO=45°，可得△OBR为等腰直角三角形，OR=OB=1，点R（0，-1），利用平移的性质可求BR解析式为，联立方程组，解方程组即可；
（3）过点A与AB垂直的直线交直线y=2x+2于U，把△AOB绕点A顺时针旋转90°，得△AO′U，AO′=AO=1，O′U=OB=b，根据点U（-1，b-1）在直线上，得出方程，求出b的值，当过点A的直线与直线平行时没有 “关联点”，OB=OW=b=2，得出在1＜b＜2时，直线上存在两个AB的“关联点”，当b＞2时，根据旋转性质将△AOB绕点A逆时针旋转90°得到△AO′U，得出AO′=AO=1，O′U=OB=b，根据点U（1,1+b）在直线上，列方程，得出即可．
（1）
解：点D与AB纵坐标相同，在直线AB上，不能构成直角三角形，
以点B为直角顶点，点B与点E横坐标相同，点E在过点B与AB垂直的直线上，
∴△ABE为直角三角形，且AE大于AB；
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 内 · · · · · · ○ · · · · · ·
号学级年名姓
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 外 · · · · · · ○ · · · · · ·
以点A为直角顶点，点A与点F横坐标相同，△AFB为直角三角形，AF=4＞AB=2，
∴点E与点F是AB关联点，
点G不在A、B两点垂直的直线上，故不能构成直角三角形，
故答案为点E，点F；
（2）
解：∵点A（0，1）点B（-1，0），OA=OB，∠AOB=90°，
∴△AOB为等腰直角三角形，AB=
∴∠ABO=∠BAO=45°，
以点A为直角顶点，过点A，与AB垂直的直线交x轴于S，
∴∠OAS=90°-∠BAO=45°，
∴△AOS为等腰直角三角形，
∴OS=OA=1，点S（1,0），
设AS解析式为代入坐标得：
，
解得，
AS解析式为，
∴，
解得，
点P（），
AP=，AP＞AB
以点B为直角顶点，过点B，与AB垂直的直线交y轴于R，
∴∠OBR=90°-∠ABO=45°，
∴△OBR为等腰直角三角形，
∴OR=OB=1，点R（0，-1），
过点R与AS平行的直线为AS直线向下平移2个单位，
则BR解析式为，
∴，
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 内 · · · · · · ○ · · · · · ·
号学级年名姓
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 外 · · · · · · ○ · · · · · ·
解得，
点P1（），
AP1=＞，
∴点P为线段AB的关联点，点P的坐标为（）或（）；
（3）
解：过点A与AB垂直的直线交直线y=2x+2于U，
把△AOB绕点A顺时针旋转90°，得△AO′U，
∴AO′=AO=1，O′U=OB=b，
点U（-1，b-1）在直线上，
∴
∴，
∴当b＞1时存在两个“关联点”，
当b＜1时，UA＜AB，不满足定义，没有两个“关联点”
当过点A的直线与直线平行时没有 “关联点”
与x轴交点X（-1，0），与y轴交点W（0，2）
∵OA=OX=1,∠XOW=∠AOB=90°，AB⊥XW，
∴△OXW顺时针旋转90°，得到△OAB，
∴OB=OW=2，
∴在1＜b＜2时，直线上存在两个AB的“关联点”，
当b＞2时，将△AOB绕点A逆时针旋转90°得到△AO′U，
∴AO′=AO=1，O′U=OB=b，
点U（1,1+b）在直线上，
∴
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 内 · · · · · · ○ · · · · · ·
号学级年名姓
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 外 · · · · · · ○ · · · · · ·
∴解得
∴当2＜b＜3时, 直线上存在两个AB的“关联点”，
当b＞3时，UA＜AB，不满足定义，没有两个“关联点”
综合得，b的取值范围1＜b＜2或2＜b＜3．
【点睛】
本题考查新定义线段的意义，直角三角形性质，仔细阅读新定义，由两个条件，（1）组成直角三角形，（2）AC＞AB，等腰直角三角形，勾股定理两点距离公式，待定系数法求直线解析式，图形旋转，两函数交点联立方程组，掌握新定义线段的意义，直角三角形性质，仔细阅读新定义，由两个条件，（1）组成直角三角形，（2）AC＞AB，等腰直角三角形，勾股定理两点距离公式，待定系数法求直线解析式，图形旋转，两函数交点联立方程组，是解题关键．
5、（1）画图见解析，基本事实：两点确定一条直线；（2）画图见解析；（3）画图见解析；（4）画图见解析；（5）
【分析】
（1）直接过AB两点画直线即可；
（2）用量角器直接画图即可；
（3）以B为圆心，BA长度为半径画圆即可；
（4）用带刻度的直尺量出AD长度取中点即可；
（5）用量角器测量各个角度大小即可；
【详解】
（1）画图如下，基本事实：两点确定一条直线
（2）画图如下；
（3）画图如下；
（4）画图如下；
（5）不唯一，正确即可．
例如：，，等
或
【点睛】
本题考查线段和角度作图，熟练使用量角器、圆规和带刻度的直尺是解题的关键．
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 内 · · · · · · ○ · · · · · ·
号学级年名姓
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 外 · · · · · · ○ · · · · · ·
一分钟跳绳个数（个）
141
144
145
146
学生人数（名）
5
2
1
2