专题6.6 解三角形-2023-2024学年高一数学下学期高效讲练测（人教A版必修第二册）

这是一份专题6.6 解三角形-2023-2024学年高一数学下学期高效讲练测（人教A版必修第二册），文件包含专题66解三角形举一反三人教A版必修第二册原卷版docx、专题66解三角形举一反三人教A版必修第二册解析版docx等2份试卷配套教学资源，其中试卷共35页， 欢迎下载使用。


TOC \ "1-3" \h \u
\l "_Tc29132" 【题型1 余弦定理边角互化的应用】 PAGEREF _Tc29132 \h 4
\l "_Tc17130" 【题型2 余弦定理解三角形】 PAGEREF _Tc17130 \h 5
\l "_Tc7605" 【题型3 正弦定理边角互化的应用】 PAGEREF _Tc7605 \h 7
\l "_Tc3026" 【题型4 正弦定理判定三角形解的个数】 PAGEREF _Tc3026 \h 8
\l "_Tc19245" 【题型5 正弦定理解三角形】 PAGEREF _Tc19245 \h 10
\l "_Tc8311" 【题型6 三角形面积公式的应用】 PAGEREF _Tc8311 \h 11
\l "_Tc5430" 【题型7 正、余弦定理判定三角形形状】 PAGEREF _Tc5430 \h 13
\l "_Tc3348" 【题型8 正、余弦定理在几何图形中的应用】 PAGEREF _Tc3348 \h 15
\l "_Tc18266" 【题型9 距离、高度、角度测量问题】 PAGEREF _Tc18266 \h 20
【知识点1 余弦定理、正弦定理】
1．余弦定理
(1)余弦定理及其推论的表示
(2)对余弦定理的理解
①余弦定理对任意的三角形都成立.
②在余弦定理中，每一个等式都包含四个量，因此已知其中三个量，利用方程思想可以求得未知的量.
③余弦定理的推论是余弦定理的第二种形式，适用于已知三角形三边来确定三角形的角的问题.用余弦
定理的推论还可以根据角的余弦值的符号来判断三角形中的角是锐角还是钝角.
④余弦定理的另一种常见变式：+-=2bcA，+-=2acB，+-=2abC.
2．正弦定理
(1)正弦定理的表示
在△ABC中，若角A,B,C对应的边分别是a,b,c，则各边和它所对角的正弦的比相等，即==.
(2)正弦定理的常见变形
在△ABC中，由正弦定理得===k(k>0)，则a=kA，b=kB，c=kC，由此可得
正弦定理的下列变形：
①=，=，=，aB=bA，aC=cA，bC=cB；
②======；
③a:b:c=A:B:C；
④===2R，（R为△ABC外接圆的半径）.
(3)三角形的边角关系
由正弦定理可推导出，在任意三角形中，有“大角对大边，小角对小边”的边角关系.
3．解三角形
(1)解三角形的概念
一般地，三角形的三个角A,B,C和它们的对边a,b,c叫做三角形的元素.在三角形中，已知三角形的几个
元素求其他元素的过程叫做解三角形.
(2)余弦定理在解三角形中的应用
利用余弦定理可以解决以下两类解三角形的问题：
①已知两边及它们的夹角，求第三边和其他两个角；
③已知三边，求三角形的三个角.
(3)正弦定理在解三角形中的应用
公式==反映了三角形的边角关系.
由正弦定理的推导过程知，该公式实际表示为：=，=，=.上述的
每一个等式都表示了三角形的两个角和它们的对边的关系.从方程角度来看，正弦定理其实描述的是三组方程，对于每一个方程，都可“知三求一”，于是正弦定理可以用来解决两类解三角形的问题：
①已知两角和任意一边，求其他的边和角，
③已知两边和其中一边的对角，求其他的边和角.
4．对三角形解的个数的研究
已知三角形的两角和任意一边，求其他的边和角，此时有唯一解，三角形被唯一确定.
已知三角形的两边和其中一边的对角，求其他的边和角，此时可能出现一解、两解或无解的情况，三
角形不能被唯一确定.
(1)从代数的角度分析“已知两边和其中一边的对角，求另一边的对角”时三角形解的情况，下面以已知
a,b和A，解三角形为例加以说明.
由正弦定理、正弦函数的有界性及三角形的性质可得：
①若B=>1，则满足条件的三角形的个数为0；
②若B==1，则满足条件的三角形的个数为1；
③若B=<1，则满足条件的三角形的个数为1或2.
显然由0角形内角和等于”等，此时需进行讨论.
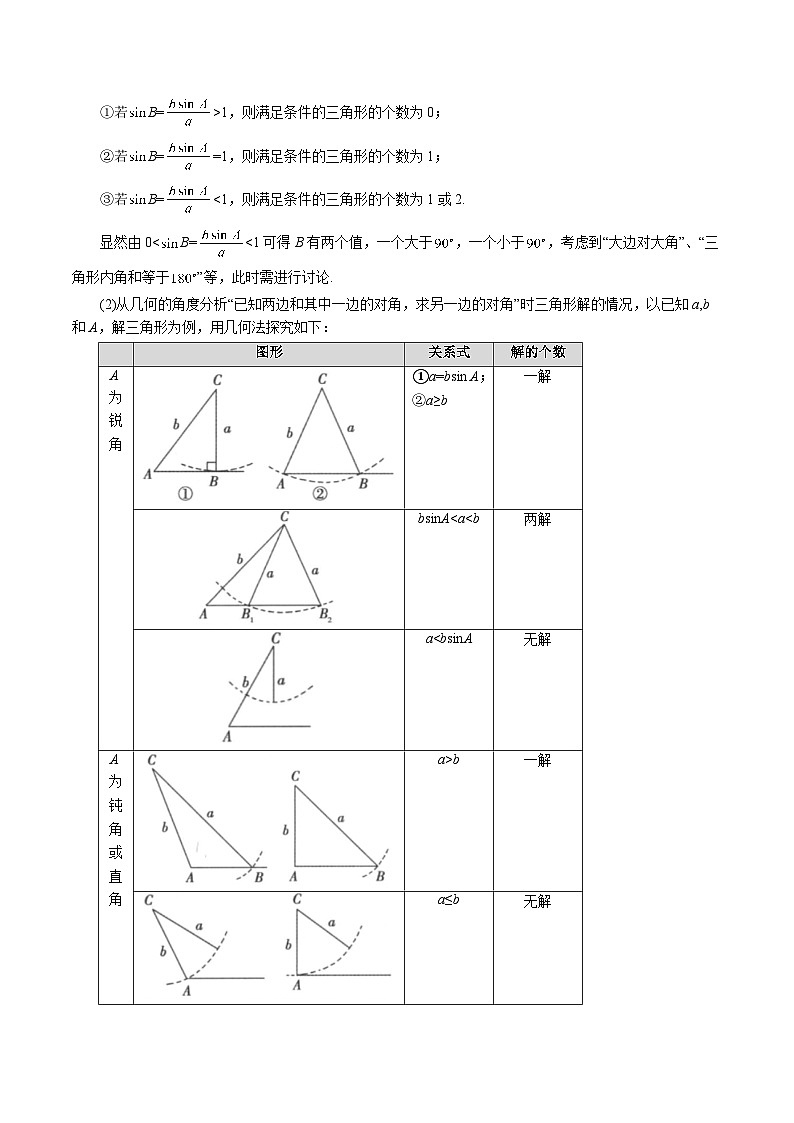
(2)从几何的角度分析“已知两边和其中一边的对角，求另一边的对角”时三角形解的情况，以已知a,b和A，解三角形为例，用几何法探究如下：
5．三角形的面积公式
(1)常用的三角形的面积计算公式
①=a=b=c (,,分别为边a,b,c上的高).
②将=bC，=cA，=aB代入上式可得=abC=bcA=acB，即三
角形的面积等于任意两边与它们夹角的正弦值乘积的一半.
(2)三角形的其他面积公式
①=r(a+b+c)= rl，其中r,l分别为△ABC的内切圆半径及△ABC的周长.
②=，=，=.
【题型1 余弦定理边角互化的应用】
【例1】（2023下·贵州黔西·高一校考期中）在△ABC中，已知a+b+cb+c−a=3bc，则角A等于（ ）
A．150°B．120°C．60°D．30°
【解题思路】根据题意结合余弦定理运算求解.
【解答过程】因为a+b+cb+c−a=3bc，整理得b2+c2−a2=bc，
由余弦定理可得csA=b2+c2−a22bc=bc2bc=12，
且0°故选：C.
【变式1-1】（2023上·陕西商洛·高二校考期末）在△ABC中，内角A,B,C的对边分别为a,b,c.若A=2π3，bc=3，且b+c=52a,则a=（ ）
A．23B．33C．22D．32
【解题思路】利用余弦定理表示出csA，利用条件变换求解即可.
【解答过程】因为A=2π3，bc=3，且b+c=52a,
由余弦定理知，
csA=b2+c2−a22bc=(b+c)2−2bc−a22bc
=14a2−2bc2bc=14a2−66
=a224−1=−12，
解得a=23，
故选：A.
【变式1-2】（2023下·陕西西安·高一校考阶段练习）在△ABC中，角A、B、C的对边分别为a、b、c，若a2=b2+c2+bc，则A的值是（ ）
A．π6B．π3C．2π3D．5π6
【解题思路】根据已知条件及余弦定理的推论即可求解.
【解答过程】由a2=b2+c2+bc，得b2+c2−a2=−bc，
由余弦定理的推理得csA=b2+c2−a22bc=−bc2bc=−12，
又因为0所以A=2π3.
故选：C.
【变式1-3】（2023下·高一课时练习）在锐角三角形ABC中，a=1，b=2，则边c的取值范围是（ ）
A．1C．3【解题思路】由锐角三角形及余弦定理列不等式组，结合三角形三边关系即可结果.
【解答过程】由题意csC=a2+b2−c22ab>0，即a2+b2=5>c2，则c<5，
同理a2+c2>b2b2+c2>a2，即c2>3，则c>3，又b−a=1综上，3故选：C.
【题型2 余弦定理解三角形】
【例2】（2023上·新疆·高二学业考试）在△ABC中，角A,B,C的对边分别是a,b,c，已知A=π3，a=3，b=1，则c等于（ ）
A．1B．2C．3−1D．3
【解题思路】利用余弦定理解三角形.
【解答过程】由余弦定理a2=b2+c2−2bccsA，
将A=π3，a=3，b=1，代入得3=12+c2−2ccsπ3，
则有c2−c−2=0，且c>0，解得c=2.
故选：B.
【变式2-1】（2023上·全国·高三专题练习）在△ABC中，AC=5， BC=10，csA=255，则AB=（ ）
A．52B．5C．10D．102
【解题思路】运用余弦定理解三角形即可.
【解答过程】由余弦定理得BC2=AB2+AC2−2AB⋅AC⋅csA，
即AB2−4AB−5=0，解得AB=5（负值已舍去）.
故选：B.
【变式2-2】（2023·海南省直辖县级单位·校考模拟预测）△ABC的内角A，B，C的对边分别为a,b,c，已知A=π3，a=7，b−c=1，则csB=（ ）
A．13B．77C．277D．714
【解题思路】根据余弦定理求得c，进而求得csB.
【解答过程】由余弦定理，a2=b2+c2−2bccsA=b2+c2−bc，
因为b−c=1,a=7，所以c2+c+12−cc+1=7，
即c2+c−6=0，解得c=2或c=−3（舍），
所以b=3,c=2，csB=a2+c2−b22ac=7+4−92×7×2=714.
故选：D.
【变式2-3】（2023上·四川成都·高二校考阶段练习）在△ABC中，∠C=π3，AC=2，M为AB边上的中点，且CM的长度为7，则BC=（ ）
A．23B．4C．27D．6
【解题思路】分别在△AMC和△BCM中利用余弦定理得到2BC2−20=AB2，在△ABC中利用余弦定理得到4+BC2−2BC=2BC2−20，然后解方程即可.
【解答过程】
在△AMC中，cs∠AMC=AM2+CM2−AC22AM⋅CM；
在△BCM中，cs∠BMC=BM2+CM2−BC22BM⋅CM；
∵∠AMC+∠BMC=π，
∴cs∠AMC=−cs∠BMC，
又AM=BM，
∴AM2+CM2−AC22AM⋅CM=−AM2+CM2−BC22AM⋅CM，整理可得：AC2+BC2=2CM2+AM2，即4+BC2=27+AM2，
∴2AM2=12AB2=BC2−10，
∴2BC2−20=AB2，
在△ABC中，AB2=AC2+BC2−2AC⋅BCcsC=4+BC2−2BC=AB2，
∴4+BC2−2BC=2BC2−20，解得：BC=−6（舍）或BC=4.
故选：B.
【题型3 正弦定理边角互化的应用】
【例3】（2023下·吉林通化·高一校考阶段练习）在△ABC中，若A:B:C=3:4:5，则a:b:c等于（ ）
A．3:4:5B．2:6:3+1
C．1:3:2D．22:23:3+2
【解题思路】利用三角形的内角和定理及正弦定理即可求解.
【解答过程】因为A:B:C=3:4:5，A+B+C=180∘，
所以A=45∘,B=60∘,C=75∘.
sin75∘=sin30∘+45∘=sin30∘cs45∘+cs30∘sin45∘=2212+32，
由正弦定理，得a:b:c=sinA:sinB:sinC=2:6:3+1.
故选：B.
【变式3-1】（2023·青海·校联考模拟预测）在△ABC中，角A,B所对的边分别为a,b.若5bsinA=2sinB，则a=（ ）
A．255B．52C．55D．455
【解题思路】根据正弦定理，即可求解.
【解答过程】根据正弦定理可知，sinA=a2R，sinB=b2R，
则5b⋅a2R=2⋅b2R，得a=255.
故选：A.
【变式3-2】（2023上·广东肇庆·高三统考阶段练习）记△ABC的内角A,B,C的对边分别为a，b，c，已知asinB=bsinC=csinA，则C=（ ）
A．π6B．π4C．π3D．π2
【解题思路】利用正弦定理变形等式，可得三角形为等边三角形，即得答案.
【解答过程】因为asinB=bsinC=csinA，
有正弦定理得，
ab=bc=ca,
则b2=ac,c2=ab，
所以b2c2=acab，故b3=c3，即b=c，
代入上边等式可得，a=b=c，
则三角形为等边三角形，
故C=π3,
故选：C.
【变式3-3】（2023下·山东青岛·高一统考期中）在△ABC中，sinA:sinB:sinC=k:k+1:2k，则k的取值范围是（ ）
A．2,+∞B．12,+∞C．12,2D．0,1
【解题思路】利用正弦定理得边长关系，再利用三角形成立条件列不等式求解即可.
【解答过程】由正弦定理asinA=bsinB=csinC及sinA:sinB:sinC=k:k+1:2k得
a:b:c=k:k+1:2k，不妨记a=mk,b=mk+1,c=2mk,(m>0)，
因为a+b>ca+c>b，所以mk+mk+1>2mkmk+2mk>mk+1，解得k>12，即k的取值范围是12,+∞.
故选：B.
【题型4 正弦定理判定三角形解的个数】
【例4】（2023·浙江·模拟预测）在△ABC中，角A,B,C所对的边分别为a,b,c.若B=π3,a=4，且该三角形有两解，则b的范围是（ ）
A．23,+∞B．23,4
C．0,4D．33,4
【解题思路】利用正弦定理推出b=23sinA，根据三角形有两解，确定角A的范围，从而结合sinA的取值范围求得答案.
【解答过程】由正弦定理得asinA=bsinB，所以b=asinBsinA=4×sinπ3sinA=23sinA,
因为该三角形有两解，故π3=B故sinA∈(32,1)，即b=23sinA∈(23,4)，
故选：B.
【变式4-1】（2023下·浙江杭州·高一校考期中）符合下列条件的三角形有且只有一个的是（ ）
A．a=1，b=2，c=3B．a=1，b=2，A=30°
C．a=1，c=3，A=30°D．a=b=1，B=30°
【解题思路】根据两边之和大于第三边及正弦定理判断三角形解的个数即可.
【解答过程】对于A，a=1，b=2，c=3，由两边之和大于第三边，1+2<3，可知符合A的三角形不存在；
对于B，由a=1，b=2，A=30°，可得sinB=22，B=45∘ 或135°，符合条件的三角形有2个，不符合题意；
对于C，a=1，c=3，A=30°，可得sinC=32>1 ，不符合题意；
对于D，a=b=1，B=30°，符合条件的三角形有一个，是等腰三角形.
故选：D.
【变式4-2】（2023上·北京海淀·高三校考开学考试）在△ABC中，a=42，A=45∘，b=m，若满足条件的△ABC有两个，则m的可能取值为（ ）
A．8B．6C．4D．2
【解题思路】根据满足条件的△ABC有两个，可得出bsinA【解答过程】因为A=45∘，a=42，b=m，且满足条件的△ABC有两个，
则bsinA故选：B.
【变式4-3】（2023下·浙江台州·高一温岭中学校考期末）在△ABC中角A,B,C所对的边分别为a,b,c，若a=1，A=30°，b=x，则（ ）
A．当x=2时，B=45°B．当x>1时，△ABC有两个解
C．当00，△ABC都有解
【解题思路】由正弦定理、正弦函数的性质计算可得.
【解答过程】因为a=1，A=30°，b=x，
所以由正弦定理asinA=bsinB，即sinB=12x，
当x=2时sinB=22，又30°当x=4时sinB=2，又0当0故选：C.
【题型5 正弦定理解三角形】
【例5】（2023下·河南省直辖县级单位·高一校考阶段练习）△ABC中，∠B=120°，AC=7，AB=5，则csC=（ ）
A．5314B．±5314C．1114D．±1114
【解题思路】根据正弦定理得到sinC=5314，再根据同角三角函数关系计算得到答案.
【解答过程】由题可得，sinB=32，由正弦定理可得ACsinB=ABsinC，所以sinC=ABACsinB=5314，
又∠B=2π3，故C∈0,π3，csC=1−sin2C=1114.
故选：C.
【变式5-1】（2023·四川成都·统考二模）在△ABC中，已知A=7π12，C=π6，AC=22，则AB边的长为（ ）
A．22B．2C．2D．−2
【解题思路】根据题意，求得B=π4，结合正弦定理，即可求解.
【解答过程】因为A=7π12，C=π6，可得B=π−A−C=π−7π12−π6=π4，
由正弦定理可得ACsinB=ABsinC,AB=ACsinCsinB=22sinπ6sinπ4=2.
故选：B.
【变式5-2】（2023上·安徽·高二校联考期中）在△ABC中，角 A，B，C所对的边分别为a，b，c，若 a=1，b=2，sinA=22，则C=（ ）
A．π6 B．π4C．π3D．π2
【解题思路】根据正弦定理，即可求解.
【解答过程】根据正弦定理asinA=bsinB，即sinB=bsinAa=1，则B=π2，
sinA=22，a故选：B.
【变式5-3】（2023·全国·模拟预测）在△ABC中，内角A,B,C的对边分别为a,b,c，
2csB−3cbcsA=3abcsC,a=3,b=4，则csA的值为（ ）
A．338B．558C．378D．38
【解题思路】先利用正弦定理、三角恒等变换等求出角B的大小，然后利用正弦定理即可求出sinA的值，进而求出csA的值．
【解答过程】由2csB−3cbcsA=3abcsC可得2bcsB=3ccsA+3acsC，
由正弦定理得2sinBcsB=3csAsinC+sinAcsC，
故2sinBcsB=3sinA+C=3sinB，
又sinB>0，所以csB=32，
因为B∈0,π，所以B=π6．
在△ABC中，由正弦定理得，asinA=bsinB，
所以sinA=38，
因为a所以csA=558．
故选B．
【题型6 三角形面积公式的应用】
【例6】（2023上·江苏镇江·高三统考期中）在△ABC中，若AB=3,AC=7,B=120°，则△ABC的面积为（ ）
A．63B．3−14C．3+14或3−14D．1534
【解题思路】利用余弦定理求BC，进而利用面积公式求面积.
【解答过程】由题意可得：AC2=AB2+BC2−2AB⋅BCcsB，即49=9+BC2+3BC，
整理得BC2+3BC−40=0，解得BC=5或BC=−8（舍去），
所以△ABC的面积为12AB⋅BC⋅sinB=12×3×5×32=1534.
故选：D.
【变式6-1】（2023·陕西西安·校联考模拟预测）在△ABC中，内角A,B,C的对边分别为a,b,c，若b=1，B=π6，1tanA+1tanC=2，则△ABC的面积为（ ）
A．14B．12C．32D．1
【解题思路】根据题意利用三角恒等变换并由正弦定理即可求得ac=1，再由面积公式即可求得结果.
【解答过程】因为1tanA+1tanC=csAsinA+csCsinC=csAsinC+sinAcsCsinAsinC=sinA+CsinAsinC
=sinπ−BsinAsinC=sinBsinAsinC=2，
所以sin2BsinAsinC=2sinB=1.由正弦定理可得b2=ac，即ac=1.
故△ABC的面积为12acsinB=12×1×12=14.
故选：A.
【变式6-2】（2023下·甘肃临夏·高一统考期末）已知△ABC的外接圆半径为4，sinB+sinC=34，sinBsinC=964，则△ABC的面积S为（ ）
A．558B．95532
C．215564D．275564
【解题思路】根据正弦定理、面积公式、二倍角的正弦公式求解.
【解答过程】由sinB+sinC=34，sinBsinC=964，
解得sinB=sinC=38，
由正弦定理可得b=2RsinB=3，c=2RsinC=3，
所以B=C，
sinA=sin(π−2B)=sin2B=2sinBcsB=2×38×1−382=34×558=35532，
∴S△ABC=12bcsinA=12×9×35532=275564.
故选：D.
【变式6-3】（2023·全国·高一专题练习）在△ABC中，内角A，B，C所对应的边分别为a，b，c，若c2=a−b2+6，且C=π3，则△ABC的面积为（ ）
A．33B．932C．3D．332
【解题思路】根据题中条件结合余弦定理先求得ab=6，进而利用面积公式求解.
【解答过程】解：∵c2=a−b2+6，∴c2=a2−2ab+b2+6
∴a2+b2−c2=2ab−6，
∵C=π3，
∴csπ3=a2+b2−c22ab=2ab−62ab=12，∴ab=6，
∴S△ABC=12absinC=12×6×32=332，
故选：D.
【题型7 正、余弦定理判定三角形形状】
【例7】（2023上·辽宁本溪·高二校考期中）在△ABC中，若sinA:sinB:sinC=4:5:6，则△ABC是（ ）
A．钝角三角形B．直角三角形
C．锐角三角形D．等边三角形
【解题思路】由正弦边角关系得a:b:c=4:5:6，设a=4t（t>0），应用余弦定理确定csC的符号，结合C为最大内角，即可得答案.
【解答过程】因为sinA:sinB:sinC=4:5:6，由正弦定理得a:b:c=4:5:6，
设a=4t（t>0），则b=5t，c=6t，
由余弦定理得csC=a2+b2−c22ab=16t2+25t2−36t22×4t×5t=18>0，则C为锐角，
又C为最大内角，故△ABC为锐角三角形.
故选：C.
【变式7-1】（2023上·河南省直辖县级单位·高二校考阶段练习）已知△ABC内角A，B，C的对边为a，b，c，若acsA2=bcsB2，c2=a2+b2−ab，则△ABC的形状是（ ）
A．钝角三角形B．等边三角形
C．直角三角形D．等腰直角三角形
【解题思路】由余弦定理求得C=60°，根据题意和正弦定理可得A=B，即可求解.
【解答过程】由c2=a2+b2−ab，得a2+b2−c2=ab，
而csC=a2+b2−c22ab=ab2ab=12，又0所以C=60°.
acsA2=bcsB2，由正弦定理得sinAcsA2=sinBcsB2，
即2sinA2csA2csA2=2sinB2csB2csB2，得sinA2=sinB2，
所以A2=B2或A2=180°−B2，得A=B或A+B=360°（舍去），
所以A=B，即△ABC为等边三角形.
故选：B.
【变式7-2】（2023上·上海松江·高二校考阶段练习）在△ABC中，角A,B,C所对的边分别为a,b,c，若b=2acsC，则△ABC为（ ）
A．直角三角形B．等边三角形
C．等腰三角形D．等腰直角三角形
【解题思路】利用余弦定理化角为边即可得解.
【解答过程】因为b=2acsC，
由余弦定理可得b=2a⋅a2+b2−c22ab=a2+b2−c2b，
所以a2+b2−c2=b2，
即a2=c2，所以a=c，
所以△ABC为等腰三角形.
故选：C.
【变式7-3】（2023上·北京·高三北京二十中校考阶段练习）在△ABC中，若csAcsB=ba ，则该三角形的形状一定是（ ）
A．等腰三角形B．等腰直角三角形
C．等腰三角形或直角三角形D．等边三角形
【解题思路】csAcsB=ba由正弦定理化简为sin2A=sin2B，然后在△ABC分析，即A=B，或2A+2B=π，从而得到结论.
【解答过程】∵ csAcsB=ba，∴ acsA=bcsB，
根据正弦定理可知：sinAcsA=sinBcsB，
∴ sin2A=sin2B，
∴在△ABC中，A=B，或2A+2B=π，即A+B=π2，即C=π2.
∴ △ABC为等腰三角形或直角三角形.
故选：C.
【题型8 正、余弦定理在几何图形中的应用】
【例8】（2023上·黑龙江哈尔滨·高三哈尔滨三中校考期末）在△ABC中，a，b，c分别为角A，B，C的对边，且3csinA+a2+b2−c22b−b−c=0.
(1)求角A的大小；
(2)若1tanB+1tanC=2tanA，且a=5，求△ABC的面积.
【解题思路】（1）由余弦定理和正弦定理，结合正弦和角公式得到3sinA−csA=1，从而得到sinA−π6=12，求出角A的大小；
（2）在（1）基础上得到1tanB+1tanC=233，结合正切和角公式得到−tanB+tanC1−tanBtanC=3，得到方程组，求出B=C=π3，得到△ABC为等边三角形，求出三角形面积.
【解答过程】（1）3csinA+a2+b2−c22b−b−c=0，
由余弦定理得3csinA+acsC−b−c=0，
由正弦定理得3sinCsinA+sinAcsC−sinB−sinC=0，
3sinCsinA+sinAcsC−sinA+C−sinC=0，
即3sinCsinA+sinAcsC−sinAcsC−csAsinC−sinC=0，
故3sinCsinA−csAsinC−sinC=0，
因为C∈0,π，所以sinC≠0，
所以3sinA−csA=1，化简得sinA−π6=12，
因为A∈0,π，所以A=π3；
（2）由（1）知A=π3，
故1tanB+1tanC=2tanA=23=233，
∵tanA=tanπ−B+C=−tanB+tanC1−tanBtanC，故−tanB+tanC1−tanBtanC=3，
联立1tanB+1tanC=233−tanB+tanC1−tanBtanC=3，解得tanB=3tanC=3，
∵B∈0,π，C∈0,π，
∴B=C=π3，
∴△ABC为等边三角形，
∴S△ABC=12bcsinA=12×5×5×32=534.
【变式8-1】（2023上·安徽合肥·高三校考期末）在△ABC内，角A，B，C所对的边分别为a，b，c，且bcsA−ccsB=a−ccsA+C．
(1)求角B的值；
(2)若△ABC的面积为33，b=13，求△ABC的周长．
【解题思路】（1）由正弦定理和三角恒等变换得到csB=12，求出角B；
（2）由余弦定理和面积公式得到方程，求出a+c，进而求出周长.
【解答过程】（1）由csA+C=−csB，得bcsA−ccsB=c−acsB
∴由正弦定理，得sinBcsA−sinCcsB=sinC−sinAcsB．
∴sinAcsB+csAsinB=2sinCcsB．
∴sinA+B=2sinCcsB．
又A+B+C=π，
∴sinA+B=sinC．
又∵0∴csB=12．
又B∈0,π，
∴B=π3．
（2）由（1）知B=π3，
∴b2=a2+c2−2accsB=a2+c2−ac①
又S=12acsinB=34ac，故34ac=33，
∴ac=12，②
又∵b=13，
∴由①②，得a2+c2−12=13，故a2+c2=25，
∴a+c2=a2+c2+2ac=25+24=49，
故a+c=7，周长为7+13.
【变式8-2】（2023上·福建泉州·高三校考阶段练习）在锐角△ABC中，角A，B，C的对边分别为a，b，c，为ccsB+bcsC=2acsA.
(1)求角A的大小；
(2)当a=3时，求b+c2的取值范围.
【解题思路】（1）利用正弦定理及正弦的和角公式计算即可；
（2）根据正弦定理先得出b+c2=sinB+sinC，根据三角形内角和性质及余弦函数的单调性计算即可.
【解答过程】（1）由正弦定理得：sinCcsB+sinBcsC=2sinAcsA，
所以sin(C+B)=2sinAcsA，即sinA=2sinAcsA，
因为sinA≠0，所以csA=12，
又A∈(0,π)，所以A=π3
（2）a=3，A=π3，由正弦定理asinA=bsinB=csinC=3sinπ3=2，
所以b+c2=sinB+sinC=sinB+sin2π3−B=32sinB+32csB=3csB−π3，
因为△ABC为锐角三角形，所以B∈(π6,π2)，则B−π3∈(−π6,π6)，
所以csB−π3∈32,1，
所以b+c2∈32,3.
【变式8-3】（2023上·山西吕梁·高三校联考阶段练习）从①(a+b+c)⋅(sinA+sinB−sinC)=asinB+2bsinA；②2asinAcsB+bsin2A=23acsC这两个条件中任选一个，补充在下面的问题中，并解答．
在△ABC中，角A，B，C所对的边分别为a，b，c，且满足：______．
(1)求角C的大小；
(2)若c=3，△ABC的内心为I，求△ABI周长的取值范围．
注：如果选择多个条件分别作答，按第一个解答计分．
【解题思路】（1）运用正余弦定理进行边角互化，借助于三角形的边角关系即可求得；
（2）先求出∠AIB，在△ABI中，通过设角θ，利用正弦定理求出三边得出三角形周长表达式，将其转化为正弦型函数，利用角的范围即可求得周长范围.
【解答过程】（1）选择条件①，(a+b+c)(sinA+sinB−sinC)=asinB+2bsinA，
在△ABC中，由正弦定理得(a+b+c)(a+b−c)=ab+2ba，
整理得a2+b2−c2=ab，则由余弦定理，csC=a2+b2−c22ab=12，
又C∈(0,π)，所以C=π3．
选择条件②，2asinAcsB+bsin2A=23acsC，
于是asinAcsB+bsinAcsA=3acsC，
在△ABC中，由正弦定理得，sin2AcsB+sinAsinBcsA=3sinAcsC，
因为sinA≠0，则sinAcsB+sinBcsA=3csC，即sin(A+B)=3csC，
因为A+B+C=π，因此sinC=3csC，即tanC=3，又C∈(0,π)，所以C=π3．
（2）
如图，由（1）知，C=π3，有∠ABC+∠BAC=2π3，
因为△ABC的内心为I，所以∠ABI+∠BAI=π3，于是∠AIB=2π3．
设∠ABI=θ，则∠BAI=π3−θ，且0<θ<π3，
在△ABI中，由正弦定理得，BIsinπ3−θ=AIsinθ=ABsin∠AIB=3sinπ3=2，
所以BI=2sinπ3−θ,AI=2sinθ，
所以△ABI的周长为3+2sinπ3−θ+2sinθ=3+232csθ−12sinθ+2sinθ =2sin(θ+π3)+3，
由0<θ<π3，得π3<θ+π3<2π3，所以sinθ+π3∈32,1，
所以△ABI周长的取值范围为(23,2+3]．
【知识点2 测量问题】
1．测量问题
(1)测量距离问题的基本类型和解决方案
当AB的长度不可直接测量时，求AB的距离有以下三种类型：
(2)测量高度问题的基本类型和解决方案
当AB的高度不可直接测量时，求AB的高度有以下三种类型：
(3)测量角度问题
测量角度问题主要涉及光线(入射角、折射角)，海上、空中的追及与拦截，此时问题涉及方向角、方
位角等概念，若是观察建筑物、山峰等，则会涉及俯角、仰角等概念.解决此类问题的关键是根据题意、图形及有关概念，确定所求的角在哪个三角形中，该三角形中已知哪些量，然后解三角形即可.
【题型9 距离、高度、角度测量问题】
【例9】（2023下·新疆乌鲁木齐·高一校考期中）如图所示，货轮在海上以40km/h的速度沿着方位角（指从正北方向顺时针转到目标方向线的水平转角）为140°的方向航行，为了确定船位，船在B点观测灯塔A的方位角为110°，航行半小时后船到达C点，观测灯塔A的方位角是65°，则货轮到达C点时，与灯塔A的距离是多少.

【解题思路】利用正弦定理可求AC的长度.
【解答过程】由题设可得∠ABC=30°，BC=40×12=20（km），
而∠ACB=40°+65°=105°，故A=180°−30°−105°=45°，
由正弦定理可得ACsin30°=20sin45°，故AC=102（km）.
【变式9-1】（2023下·广东湛江·高一校考阶段练习）为了应对日益严重的气候问题，某气象仪器科研单位研究出一种新的“弹射型”气候仪器，这种仪器可以弹射到空中进行气候观测，B，C，D三地位于同一水平面上，这种仪器在B地进行弹射实验，C,D两地相距100m，∠BCD=60°，在C地听到弹射声音的时间比D地晚217秒，在C地测得该仪器至最高点A处的仰角为30°．（已知声音的传播速度为340m/s），求：

(1)B，C两地间的距离；
(2)这种仪器的垂直弹射高度AB．
【解题思路】（1）设BC=x，利用在C地听到弹射声音的时间比D地晚217秒，表示出BD，再由余弦定理，即可得解；
（2）解Rt△ABC即可得解．
【解答过程】（1）设BC=x，
∵在C地听到弹射声音的时间比D地晚217秒，
∴BD=x−217×340=x−40，
在△BCD中，由余弦定理BD2=BC2+CD2−2BC⋅CD⋅cs∠BCD，
∴x−402=x2+10000−100x，解得x=420，
故B，C两地间的距离为420米；
（2）在△ABC中，BC=420，
∴AB=BC⋅tan∠ACB=420×33=1403米，
故该仪器的垂直弹射高度AB为1403米．
【变式9-2】（2023下·上海静安·高一统考期末）如图，某人位于临河的公路上，已知公路两个相邻路灯A、B之间的距离是100m，为了测量点A与河对岸一点C之间的距离，此人先后测得∠BAC=75°，∠ABC=60°.

(1)求A、C两点之间的距离；
(2)假设你只携带着量角器（可以测量以你为顶点的角的大小）.请你设计一个通过测量角可以计算出河对岸两点C、D之间距离的方案，用字母表示所测量的角的大小，并用其表示出CD的长.
【解题思路】（1）在△ABC中利用正弦定理直接求解即可；
（2）测得∠DAB=α，∠ABD=β，∠CAD=θ，在△ABD中利用正弦定理求出AD，再在△ACD中利用余弦定理可求出CD
【解答过程】（1）在△ABC中，由正弦定理，有
ACsinB=ABsin180°−A−B，
即AC=100sin60°sin45°=506.
答：A、C两点之间的距离为506m.
（2）测得∠DAB=α，∠ABD=β，∠CAD=θ.
在△ABD中，由正弦定理，有
ADsinβ=ABsin180°−α−β，即AD=100sinβsinα+β.
在△ACD中，由余弦定理，有CD=AC2+AD2−2AC×ADcsθ
=15000+10000sin2βsin2α+β−100006sinβsinα+βcsθ或10032+sin2βsin2α+β−6sinβsinα+βcsθ.
【变式9-3】（2023下·河南郑州·高一校联考期中）在海岸A处，发现北偏西75°的方向，与A距离2海里的B处有一艘走私船，在A处北偏东45°方向，与A距离（3−1）海里的C处的缉私船奉命以103海里/小时的速度追截走私船．此时，走私船正以10海里/小时的速度从B向北偏西30°方向逃窜，问：

(1)刚发现走私船时，缉私船距离走私船多远？在走私船的什么方向？
(2)缉私船沿什么方向能最快追上走私船？
【解题思路】（1）根据题求得BC=6，由正弦定理求得sin∠ACB=22，得到∠ACB=45°，得出BC为水平线，即可得到答案；
（2）设经过时间t小时后，缉私船追上走私船，得到BD=10t,CD=103t,∠DBC=120°，结合正弦定理求得∠BCD=30°，进而得到答案.
【解答过程】（1）由题意，可得AB=2,AC=3−1,∠BAC=120°，
则BC= AB2+AC2−2AB⋅AC⋅cs∠BAC=4+4－23+23−2=6，
在△ABC中，由正弦定理ABsin∠ACB＝BCsin∠BAC，即2sin∠ACB＝632，
解得sin∠ACB=22，因为0°<∠ACB<180°，所以∠ACB=45°，所以BC为水平线，
所以刚发现走私船时，缉私船距离走私船6海里，在走私船的正东方向．
（2）设经过时间t小时后，缉私船追上走私船，
在△BCD中，可得BD=10t,CD=103t,∠DBC=120°，
由正弦定理得sin∠BCD=BDsin∠CBDCD=10t×32103t=12，
因为∠BCD为锐角，所以∠BCD=30°，
所以缉私船沿北偏西60°的方向能最快追上走私船．文字表述
三角形中任何一边的平方，等于其他两边平方的和减去这两边与它们夹角的余弦的积的两倍.
公式表述
a2=b2+c2-2bccsA，b2=a2+c2-2accsB，c2=a2+b2-2abcsC.
推论
图形
关系式
解的个数
A为锐角
①a=bsin A；
②a≥b
一解
bsinA两解
a无解
A为钝角或直角
a>b
一解
a≤b
无解
类型
简图
计算方法
A,B间不可达也不可视
测得AC=b，BC=a，C的大小，则由余弦定理得
B, C与点A可视但不可达
测得BC=a，B，C的大小，则A=π-(B+ C)，由正弦定理得
C,D与点A,B均可视不可达
测得CD=a及∠BDC,∠ACD,∠BCD,∠ADC的度数.在△ACD中，用正弦定理求AC；在△BCD中，用正弦定理求BC；在△ABC中，用余弦定理求AB.
类型
简图
计算方法
底部
可达
测得BC=a，C的大小，AB=a·tan C.
底部不可达
点B与C,D共线
测得CD=a及∠ACB与∠ADB的度数.
先由正弦定理求出AC或AD,再解直角三角形得AB的值.
点B与C , D不共线
测得CD=a及∠BCD,∠BDC,∠ACB的度数.
在△BCD中由正弦定理求得BC，再解直角三角形得AB的值.