
人教版八年级数学上册同步精品压轴题专题02全等三角形中的六种模型梳理(学生版+解析)
展开类型一、倍长中线模型
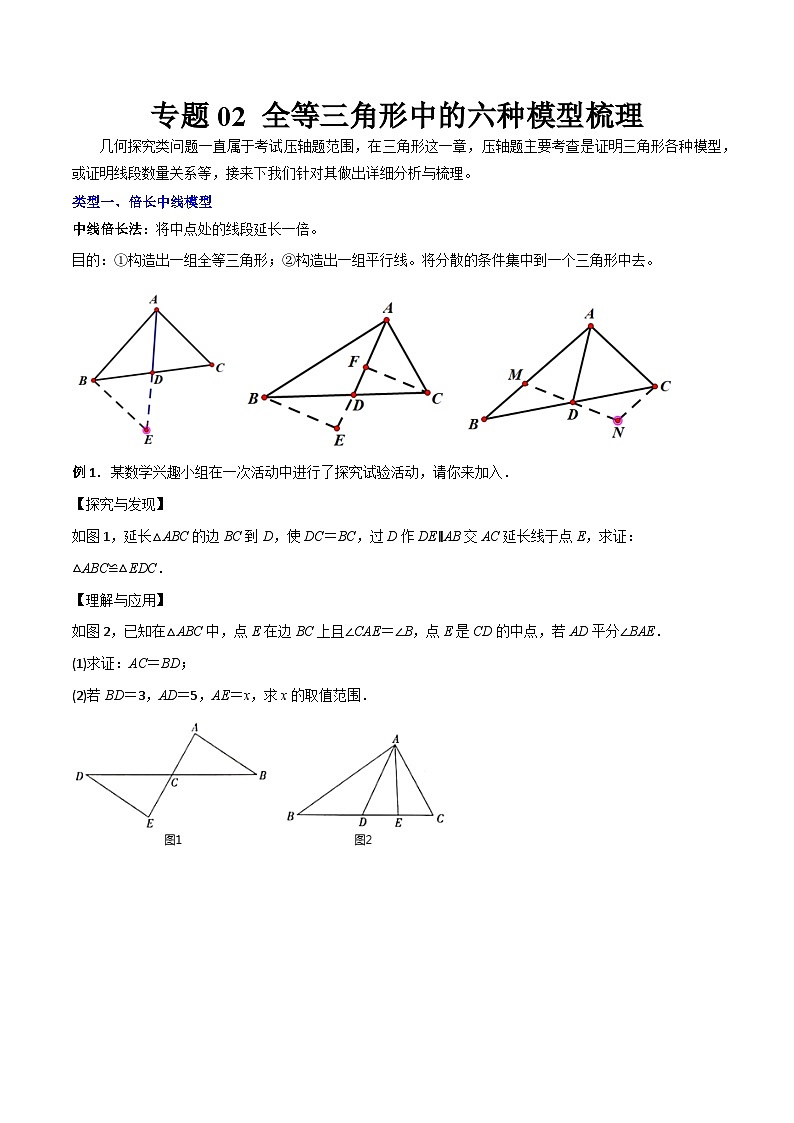
中线倍长法:将中点处的线段延长一倍。
目的: = 1 \* GB3 ①构造出一组全等三角形; = 2 \* GB3 ②构造出一组平行线。将分散的条件集中到一个三角形中去。
例1.某数学兴趣小组在一次活动中进行了探究试验活动,请你来加入.
【探究与发现】
如图1,延长△ABC的边BC到D,使DC=BC,过D作DE∥AB交AC延长线于点E,求证:△ABC≌△EDC.
【理解与应用】
如图2,已知在△ABC中,点E在边BC上且∠CAE=∠B,点E是CD的中点,若AD平分∠BAE.
(1)求证:AC=BD;
(2)若BD=3,AD=5,AE=x,求x的取值范围.
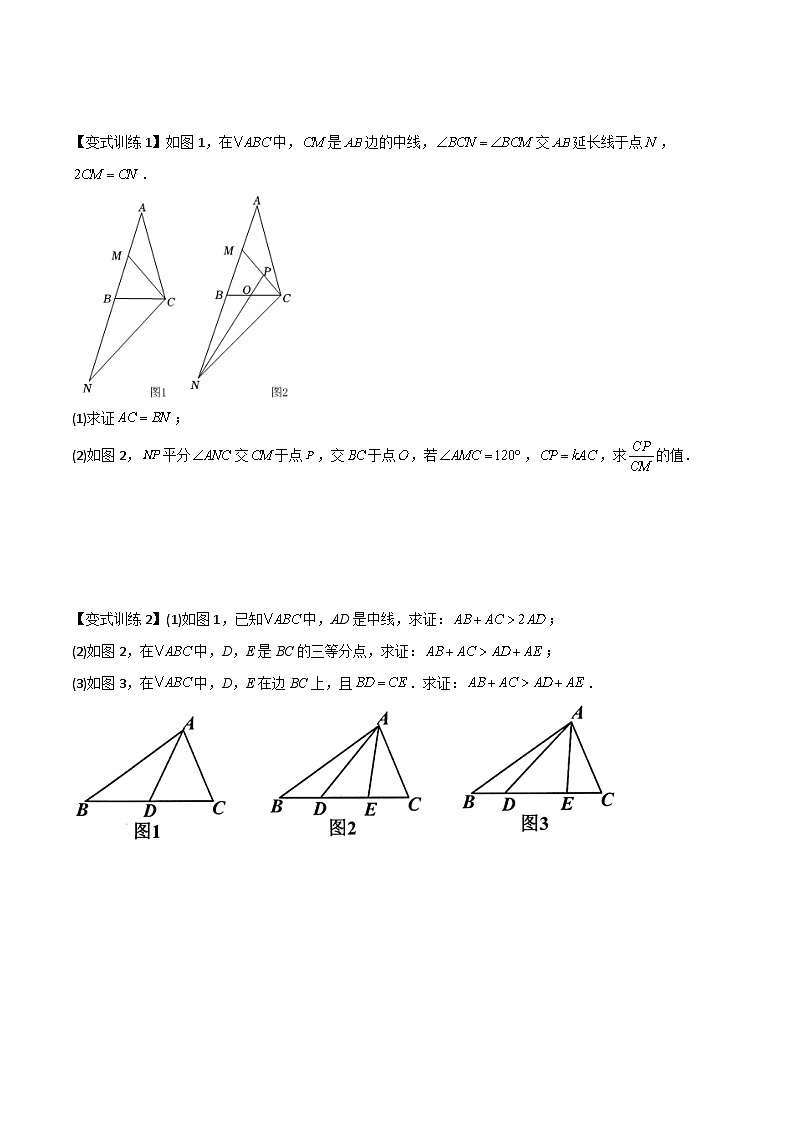
【变式训练1】如图1,在中,是边的中线,交延长线于点,.
(1)求证;
(2)如图2,平分交于点,交于点,若,,求的值.
【变式训练2】(1)如图1,已知中,AD是中线,求证:;
(2)如图2,在中,D,E是BC的三等分点,求证:;
(3)如图3,在中,D,E在边BC上,且.求证:.
【变式训练3】在中,点为边中点,直线绕顶点旋转,直线于点.直线于点,连接,.
(1)如图1,若点,在直线的异侧,延长交于点.求证:.
(2)若直线绕点旋转到图2的位置时,点,在直线的同侧,其它条件不变,此时,,,求的长度.
(3)若过点作直线于点.试探究线段、和的关系.
类型二、截长补短模型
截长补短法使用范围:线段和差的证明(往往需证2次全等)
例.在等边三角形ABC的两边AB、AC所在直线上分别有两点M、N,P为△ABC外一点,且∠MPN=60°,∠BPC=120°,BP=CP.探究:当点M、N分别在直线AB、AC上移动时,BM,NC,MN之间的数量关系.
(1)如图①,当点M、N在边AB、AC上,且PM=PN时,试说明MN=BM+CN.
(2)如图②,当点M、N在边AB、AC上,且PM≠PN时,MN=BM+CN还成立吗?
答: .(请在空格内填“一定成立”“不一定成立”或“一定不成立”).
(3)如图③,当点M、N分别在边AB、CA的延长线上时,请直接写出BM,NC,MN之间的数量关系.
【变式训练1】如图,在四边形中,,点E、F分别在直线、上,且.
(1)当点E、F分别在边、上时(如图1),请说明的理由.
(2)当点E、F分别在边、延长线上时(如图2),(1)中的结论是否仍然成立?若成立,请说明理由;若不成立,请写出、、之间的数量关系,并说明理由.
【变式训练2】(1)阅读理解:问题:如图1,在四边形中,对角线平分,.求证:.
思考:“角平分线+对角互补”可以通过“截长、补短”等构造全等去解决问题.
方法1:在上截取,连接,得到全等三角形,进而解决问题;
方法2:延长到点,使得,连接,得到全等三角形,进而解决问题.
结合图1,在方法1和方法2中任选一种,添加辅助线并完成证明.
(2)问题解决:如图2,在(1)的条件下,连接,当时,探究线段,,之间的数量关系,并说明理由;
(3)问题拓展:如图3,在四边形中,,,过点D作,垂足为点E,请直接写出线段、、之间的数量关系.
【变式训练3】在中,BE,CD为的角平分线,BE,CD交于点F.
(1)求证:;
(2)已知.
①如图1,若,,求CE的长;
②如图2,若,求的大小.
类型三、做平行线证明全等
例1.如图所示:是等边三角形,、分别是及延长线上的一点,且,连接交于点.
求让:
【变式训练1】 P为等边△ABC的边AB上一点,Q为BC延长线上一点,且PA=CQ,连PQ交AC边于D.
(1)证明:PD=DQ.
(2)如图2,过P作PE⊥AC于E,若AB=6,求DE的长.
【变式训练2】已知在等腰△ABC中,AB=AC,在射线CA上截取线段CE,在射线AB上截取线段BD,连接DE,DE所在直线交直线BC与点M.请探究:
(1)如图(1),当点E在线段AC上,点D在AB延长线上时,若BD=CE,请判断线段MD和线段ME的数量关系,并证明你的结论.
(2)如图(2),当点E在CA的延长线上,点D在AB的延长线上时,若BD=CE,则(1)中的结论还成立吗?如果成立,请证明;如果不成立,说明理由;
类型四、旋转模型
例.如图1,,,,、相交于点,连接.
(1)求证:,并用含的式子表示的度数;
(2)当时,取,的中点分别为点、,连接,,,如图2,判断的形状,并加以证明.
【变式训练1】四边形是由等边和顶角为的等腰排成,将一个角顶点放在处,将角绕点旋转,该交两边分别交直线、于、,交直线于、两点.
(1)当、都在线段上时(如图1),请证明:;
(2)当点在边的延长线上时(如图2),请你写出线段,和之间的数量关系,并证明你的结论;
(3)在(1)的条件下,若,,请直接写出的长为 .
【变式训练2】(1)问题发现:
如图1,△ACB和△DCE均为等边三角形,当△DCE旋转至点A,D,E在同一直线上,连接BE.则:
①∠AEB的度数为 °;
②线段AD、BE之间的数量关系是 .
(2)拓展研究:
如图2,△ACB和△DCE均为等腰三角形,且∠ACB=∠DCE=90°,点 A、D、E在同一直线上,若AD=a,AE=b,AB=c,求a、b、c之间的数量关系.
(3)探究发现:
图1中的△ACB和△DCE,在△DCE旋转过程中,当点A,D,E不在同一直线上时,设直线AD与BE相交于点O,试在备用图中探索∠AOE的度数,直接写出结果,不必说明理由.
【变式训练3】如图1,在中,,,点,分别在边,上,,连接,点,,分别为,,的中点.
(1)观察猜想:图1中,线段与的数量关系是______,位置关系是______.
(2)探究证明:把绕点逆时针方向旋转到图2的位置,连接,,,判断的形状,并说明理由;
(3)拓展延伸:把绕点在平面内自由旋转,若,,请直接写出面积的最大值.
类型五、手拉手模型
例.在等边中,点D在AB上,点E在BC上,将线段DE绕点D逆时针旋转60°得到线段DF,连接CF.
(1)如图(1),点D是AB的中点,点E与点C重合,连接AF.若,求AF的长;
(2)如图(2),点G在AC上且,求证:;
(3)如图(3),,,连接AF.过点F作AF的垂线交AC于点P,连接BP、DP.将沿着BP翻折得到,连接QC.当的周长最小时,直接写出的面积.
【变式训练1】△ACB和△DCE是共顶点C的两个大小不一样的等边三角形.
(1)问题发现:
如图1,若点A,D,E在同一直线上,连接AE,BE.
①求证:△ACD≌△BCE;②求∠AEB的度数.
(2)类比探究:如图2,点B、D、E在同一直线上,连接AE,AD,BE,CM为△DCE中DE边上的高,请求∠ADB的度数及线段DB,AD,DM之间的数量关系,并说明理由.
(3)拓展延伸:如图3,若设AD(或其延长线)与BE的所夹锐角为α,则你认为α为多少度,并证明.
【变式训练2】(1)如图1,锐角△ABC中,分别以AB、AC为边向外作等腰直角△ABE和等腰直角△ACD,使AE=AB,AD=AC,∠BAE=∠CAD=90°,连接BD,CE,试猜想BD与CE的大小关系,不需要证明.
【深入探究】(2)如图2,四边形ABCD中,AB=5,BC=2,∠ABC=∠ACD=∠ADC=45°,求BD2的值;甲同学受到第一问的启发构造了如图所示的一个和△ABD全等的三角形,将BD进行转化再计算,请你准确的叙述辅助线的作法,再计算;
【变式思考】(3)如图3,四边形ABCD中,AB=BC,∠ABC=60°,∠ADC=30°,AD=6,BD=10,则CD= .
【变式训练3】(1)问题发现:
如图1,和均为等腰直角三角形,,连接,,点、、在同一条直线上,则的度数为__________,线段、之间的数量关系__________;
(2)拓展探究:
如图2,和均为等腰直角三角形,,连接,,点、、不在一条直线上,请判断线段、之间的数量关系和位置关系,并说明理由.
(3)解决问题:
如图3,和均为等腰三角形,,则直线和的夹角为__________.(请用含的式子表示)
类型六、一线三角模型
例.在中,,,直线MN经过点C且于D,于E.
(1)当直线MN绕点C旋转到图1的位置时,求证:
①≌;
②;
(2)当直线MN烧点C旋转到图2的位置时,求证:;
(3)当直线MN绕点C旋转到图3的位置时,试问DE、AD、BE具有怎样的等量关系?请写出这个等量关系,并加以证明.
【变式训练1】【问题解决】
(1)已知△ABC中,AB=AC,D,A,E三点都在直线l上,且有∠BDA=∠AEC=∠BAC.如图①,当∠BAC=90°时,线段DE,BD,CE的数量关系为:______________;
【类比探究】
(2)如图②,在(1)的条件下,当0°<∠BAC<180°时,线段DE,BD,CE的数量关系是否变化,若不变,请证明:若变化,写出它们的关系式;
【拓展应用】
(3)如图③,AC=BC,∠ACB=90°,点C的坐标为(-2,0),点B的坐标为(1,2),请求出点A的坐标.
【变式训练2】(1)如图1,在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D、E.求证:△ABD≌△CAE;
(2)如图2,将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意锐角或钝角.请问结论△ABD≌△CAE是否成立?如成立,请给出证明;若不成立,请说明理由.
(3)拓展应用:如图3,D,E是D,A,E三点所在直线m上的两动点(D,A,E三点互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD,CE,若∠BDA=∠AEC=∠BAC,求证:△DEF是等边三角形.
【变式训练3】探究:(1)如图(1),已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D、E.请直接写出线段BD,DE,CE之间的数量关系是 .
拓展:(2)如图(2),将探究中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意锐角或钝角.请问探究中的结论是否成立?如成立,请你给出证明;若不成立,请说明理由.
应用:(3)如图(3),D、E是D、A、E三点所在直线m上的两动点(D、A、E三点互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD、CE,若∠BDA=∠AEC=∠BAC,请直接写出△DEF的形状是 .
专题02 全等三角形中的六种模型梳理
几何探究类问题一直属于考试压轴题范围,在三角形这一章,压轴题主要考查是证明三角形各种模型,或证明线段数量关系等,接来下我们针对其做出详细分析与梳理。
类型一、倍长中线模型
中线倍长法:将中点处的线段延长一倍。
目的: = 1 \* GB3 ①构造出一组全等三角形; = 2 \* GB3 ②构造出一组平行线。将分散的条件集中到一个三角形中去。
例1.某数学兴趣小组在一次活动中进行了探究试验活动,请你来加入.
【探究与发现】
如图1,延长△ABC的边BC到D,使DC=BC,过D作DE∥AB交AC延长线于点E,求证:△ABC≌△EDC.
【理解与应用】
如图2,已知在△ABC中,点E在边BC上且∠CAE=∠B,点E是CD的中点,若AD平分∠BAE.
(1)求证:AC=BD;
(2)若BD=3,AD=5,AE=x,求x的取值范围.
【答案】[探究与发现]见解析;[理解与应用](1)见解析;(2)1<x<4
【详解】解:[探究与发现]
证明:∵DE∥AB,∴∠B=∠D,
又∵BC=DC,∠ACB=∠ECD,∴△ABC≌△EDC(ASA);
[理解与应用](1)证明:如图2中,延长AE到F,使EF=EA,连接DF,
∵点E是CD的中点,∴ED=EC,
在△DEF与△CEA中,,∴△DEF≌△CEA(SAS),∴AC=FD,∴∠AFD=∠CAE,
∵∠CAE=∠B,∴∠AFD=∠B,∵AD平分∠BAE,∴∠BAD=∠FAD,
在△ABD与△AFD中,,∴△ABD≌△AFD(AAS),∴BD=FD,∴AC=BD;
(2)解:由(1)得:AF=2AE=2x,△ABD≌△AFD,∴AB=AF=2x,
∵BD=3,AD=5,
在△ABD中,由三角形的三边关系得:AD-BD<AB<AD+BD,即5-3<2x<5+3,解得:1<x<4,
即x的取值范围是1<x<4.
【变式训练1】如图1,在中,是边的中线,交延长线于点,.
(1)求证;
(2)如图2,平分交于点,交于点,若,,求的值.
【答案】(1)见解析;(2)
【详解】(1)如图1所示,延长至点,使,
在与中,,,,,,
在与中,,,,;
(2)如图所示,,,
平分,,,
,,,作,
在与中,,,,,
在与中,,,,,,设,,,.
【变式训练2】(1)如图1,已知中,AD是中线,求证:;
(2)如图2,在中,D,E是BC的三等分点,求证:;
(3)如图3,在中,D,E在边BC上,且.求证:.
【答案】(1)见解析;(2)见解析;(3)见解析
【详解】证:(1)如图所示,延长AD至P点,使得AD=PD,连接CP,
∵AD是△ABC的中线,∴D为BC的中点,BD=CD,
在△ABD与△PCD中,,∴△ABD≌△PCD(SAS),∴AB=CP,
在△APC中,由三边关系可得AC+PC>AP,∴;
(2)如图所示,取DE中点H,连接AH并延长至Q点,使得AH=QH,连接QE和QC,
∵H为DE中点,D、E为BC三等分点,∴DH=EH,BD=DE=CE,∴DH=CH,
在△ABH和△QCH中,,∴△ABH≌△QCH(SAS),
同理可得:△ADH≌△QEH,∴AB=CQ,AD=EQ,
此时,延长AE,交CQ于K点,
∵AC+CQ=AC+CK+QK,AC+CK>AK,∴AC+CQ>AK+QK,
又∵AK+QK=AE+EK+QK,EK+QK>QE,∴AK+QK>AE+QE,
∴AC+CQ>AK+QK>AE+QE,
∵AB=CQ,AD=EQ,∴;
(3)如图所示,取DE中点M,连接AM并延长至N点,使得AM=NM,连接NE,CE,
∵M为DE中点,∴DM=EM,∵BD=CE,∴BM=CM,
在△ABM和△NCM中,,∴△ABM≌△NCM(SAS),
同理可证△ADM≌△NEM,∴AB=NC,AD=NE,
此时,延长AE,交CN于T点,
∵AC+CN=AC+CT+NT,AC+CT>AT,∴AC+CN>AT+NT,
又∵AT+NT=AE+ET+NT,ET+NT>NE,∴AT+NT>AE+NE,∴AC+CN>AT+NT>AE+NE,
∵AB=NC,AD=NE,∴.
【变式训练3】在中,点为边中点,直线绕顶点旋转,直线于点.直线于点,连接,.
(1)如图1,若点,在直线的异侧,延长交于点.求证:.
(2)若直线绕点旋转到图2的位置时,点,在直线的同侧,其它条件不变,此时,,,求的长度.
(3)若过点作直线于点.试探究线段、和的关系.
【答案】(1)见解析;(2);(3)线段、和的位置关系为,数量关系为或或
【详解】(1)证明:如图1,
直线于点,直线于点,,,,
又为边中点,,
在和中,,,.
(2)解:如图2,延长与的延长线相交于点,
直线于点,直线于点,,
,,,
又为中点,,
又,∴在和中,,,
,,,
∵,,,
,,,,
.
(3)位置关系:,数量关系:分四种情况讨论
∵直线于点.直线于点,直线于点,
∴,
①如图3,当直线与线段交于一点时,
由(1)可知,,即,,
,,
∵,.
②当直线与线段交于一点时,如图,延长交的延长线于点.
直线于点,直线于点,
,,,
又为边中点,,
在和中,,,.
,即,,
,,
∵,.
③如图4,当直线与线段的延长线交于一点时.
由(2)得:,,,
∴,即,
.
④当直线与线段的延长线交于一点时,
如图,延长交的延长线于点.
直线于点,直线于点,
,,
,,
又为中点,,
又,∴在和中,,,
,,∴,即,
.
综上所述,线段、和的位置关系为,数量关系为或或.
类型二、截长补短模型
截长补短法使用范围:线段和差的证明(往往需证2次全等)
例.在等边三角形ABC的两边AB、AC所在直线上分别有两点M、N,P为△ABC外一点,且∠MPN=60°,∠BPC=120°,BP=CP.探究:当点M、N分别在直线AB、AC上移动时,BM,NC,MN之间的数量关系.
(1)如图①,当点M、N在边AB、AC上,且PM=PN时,试说明MN=BM+CN.
(2)如图②,当点M、N在边AB、AC上,且PM≠PN时,MN=BM+CN还成立吗?
答: .(请在空格内填“一定成立”“不一定成立”或“一定不成立”).
(3)如图③,当点M、N分别在边AB、CA的延长线上时,请直接写出BM,NC,MN之间的数量关系.
【答案】(1)见解析;(2)一定成立;(3)MN=NC﹣BM
【解析】(1)证明:∵△ABC为等边三角形,∴∠ABC=∠ACB=60°,
∵∠BPC=120°,BP=CP,∴∠PBC=∠PCB=×(180°﹣120°)=30°,∴∠PBM=∠PCN=90°,
在Rt△PBM和Rt△PCN中,,∴Rt△PBM≌Rt△PCN(HL),∴∠BPM=∠CPN=30°,
∵∠MPN=60°,PM=PN,∴△PMN为等边三角形,∴PM=PN=MN,
在Rt△PBM中,∠BPM=30°,∴BM=PM,同理可得,CN=PN,∴BM+CN=MN.
(2)解:一定成立,理由如下:延长AC至H,使CH=BM,连接PH,如图所示,
由(1)可知:∠PBM=∠PCN=90°,∴∠PCH=90°,∴∠PBM=∠PCH,
在△PBM和△PCH中,,∴△PBM≌△PCH(SAS),∴PM=PH,∠BPM=∠CPH,
∵∠BPM+∠CPN=60°,∴∠CPN+∠CPH=60°,∴∠MPN=∠HPN,
在△MPN和△HPN中,,∴△MPN≌△HPN(SAS),∴MN=HN=BM+CN,
故答案为:一定成立.
(3)解:在AC上截取CK=BM,连接PK,如图所示,
在△PBM和△PCK中,,∴△PBM≌△PCK(SAS),
∴PM=PK,∠BPM=∠CPK,
∵∠BPM+∠BPN=60°,∴∠CPK+∠BPN=60°,∴∠KPN=60°,∴∠MPN=∠KPN,
在△MPN和△KPN中,,∴△MPN≌△KPN(SAS),∴MN=KN,
∵KN=NC﹣CK=NC﹣BM,∴MN=NC﹣BM.
【变式训练1】如图,在四边形中,,点E、F分别在直线、上,且.
(1)当点E、F分别在边、上时(如图1),请说明的理由.
(2)当点E、F分别在边、延长线上时(如图2),(1)中的结论是否仍然成立?若成立,请说明理由;若不成立,请写出、、之间的数量关系,并说明理由.
【答案】(1)见解析;(2)不成立,,见解析
【解析】(1)EF=BE+DF,
理由:延长EB至G,使BG=DF,连接AG,
∵∠ABC+∠ADC=180°,∠ABC+∠ABG=180°,∴∠ADC=∠ABG,
在△ABG和△ADF中,,∴△ABG≌△ADF(SAS),∴AG=AF,∠BAG=∠DAF,
∵∠EAF=∠BAD,∴∠BAE+∠DAF=∠BAE+∠BAG=∠EAF,即∠EAG=∠EAF,
在△EAG和△EAF中,,∴△EAG≌△EAF(SAS),∴GE=EF,∴EF=BE+DF;
(2)(1)中结论不成立,EF=BE﹣FD,
在BE上截取BM=DF,连接AM,
∵∠ABC+∠ADC=180°,∠ADC+∠ADF=180°,∴∠ABC=∠ADF,
在△ABM和△ADF中,,∴△ABM≌△ADF(SAS),∴AM=AF,∠BAM=∠DAF,
∵∠BAM+∠MAD=∠DAF+∠MAD,∴∠BAD=∠MAF,
∵∠EAF=∠BAD,∴∠EAF=∠MAF,∴∠EAF=∠EAM,
在△AME和△AFE中,,∴△AME≌△AFE(SAS),
∴ME=EF,∴ME=BE﹣BM=BE﹣DF,∴EF=BE﹣FD.
【变式训练2】(1)阅读理解:问题:如图1,在四边形中,对角线平分,.求证:.
思考:“角平分线+对角互补”可以通过“截长、补短”等构造全等去解决问题.
方法1:在上截取,连接,得到全等三角形,进而解决问题;
方法2:延长到点,使得,连接,得到全等三角形,进而解决问题.
结合图1,在方法1和方法2中任选一种,添加辅助线并完成证明.
(2)问题解决:如图2,在(1)的条件下,连接,当时,探究线段,,之间的数量关系,并说明理由;
(3)问题拓展:如图3,在四边形中,,,过点D作,垂足为点E,请直接写出线段、、之间的数量关系.
【答案】(1)证明见解析;(2);理由见解析;(3).
【详解】解:(1)方法1:在上截,连接,如图.
平分,.
在和中,,,,.
,..,.
方法2:延长到点,使得,连接,如图.
平分,.
在和中,,.,.
,.,,.
(2)、、之间的数量关系为:.
(或者:,).
延长到点,使,连接,如图2所示.
由(1)可知,.为等边三角形.,.
,..
,为等边三角形.,.
,,即.
在和中,,.,
,.
(3),,之间的数量关系为:.
(或者:,)
解:连接,过点作于,如图3所示.
,..
在和中,,,,.
在和中,,.,
,.
【变式训练3】在中,BE,CD为的角平分线,BE,CD交于点F.
(1)求证:;
(2)已知.
①如图1,若,,求CE的长;
②如图2,若,求的大小.
【答案】(1)证明见解析;(2)2.5;(3)100°.
【解析】解:(1)、分别是与的角平分线,
,,,
(2)如解(2)图,在BC上取一点G使BG=BD,
由(1)得,
,,∴,
在与中, ,∴(SAS)
∴,∴,∴,∴
在与中,,,,
,;∵,,∴
(3)如解(3)图,延长BA到P,使AP=FC,
,∴,
在与中, ,∴(SAS)∴,,
∴,
又∵,∴,
又∵,∴,∴,,
∴,
类型三、做平行线证明全等
例1.如图所示:是等边三角形,、分别是及延长线上的一点,且,连接交于点.
求让:
【答案】见详解
【详解】过点D作DE∥AC,交BC于点E,∵是等边三角形,∴∠B=∠ACB=60°,
∵DE∥AC,∴∠DEB=∠ACB=60°,∠MDE=∠MEC,∴是等边三角形,∴BD=DE,
∵,∴DE=CE,
又∵∠EMD=∠CME,∴∆EMD≅∆CME,∴.
【变式训练1】 P为等边△ABC的边AB上一点,Q为BC延长线上一点,且PA=CQ,连PQ交AC边于D.
(1)证明:PD=DQ.
(2)如图2,过P作PE⊥AC于E,若AB=6,求DE的长.
【答案】(1)证明见解析;(2)DE=3.
【详解】(1)如图1所示,点P作PF∥BC交AC于点F.
∵△ABC是等边三角形,∴△APF也是等边三角形,AP=PF=AF=CQ.
∵PF∥BC,∴∠PFD=∠DCQ.在△PDF和△QDC中,,∴△PDF≌△QDC(AAS),
∴PD=DQ;
(2)如图2所示,过P作PF∥BC交AC于F.∵PF∥BC,△ABC是等边三角形,
∴∠PFD=∠QCD,△APF是等边三角形,∴AP=PF=AF.
∵PE⊥AC,∴AE=EF.
∵AP=PF,AP=CQ,∴PF=CQ.在△PFD和△QCD中,,
∴△PFD≌△QCD(AAS),∴FD=CD.
∵AE=EF,∴EF+FD=AE+CD,∴AE+CD=DEAC.
∵AC=6,∴DE=3.
【变式训练2】已知在等腰△ABC中,AB=AC,在射线CA上截取线段CE,在射线AB上截取线段BD,连接DE,DE所在直线交直线BC与点M.请探究:
(1)如图(1),当点E在线段AC上,点D在AB延长线上时,若BD=CE,请判断线段MD和线段ME的数量关系,并证明你的结论.
(2)如图(2),当点E在CA的延长线上,点D在AB的延长线上时,若BD=CE,则(1)中的结论还成立吗?如果成立,请证明;如果不成立,说明理由;
【答案】(1)DM=EM.理由见详解;(2)成立,理由见详解;(3)MD=ME.
【解析】(1)解:DM=EM;证明:过点E作EF//AB交BC于点F,
∵AB=AC,∴∠ABC=∠C;
又∵EF//AB,∴∠ABC=∠EFC,∴∠EFC=∠C,∴EF=EC.
又∵BD=EC,∴EF=BD.
又∵EF//AB,∴∠ADM=∠MEF.
在△DBM和△EFM中 ,∴△DBM≌△EFM,∴DM=EM.
(2)解:成立;证明:过点E作EF//AB交CB的延长线于点F,
∵AB=AC,∴∠ABC=∠C;
又∵EF//AB,∴∠ABC=∠EFC,∴∠EFC=∠C,∴EF=EC.
又∵BD=EC,∴EF=BD.
又∵EF//AB,∴∠ADM=∠MEF.
在△DBM和△EFM中∴△DBM≌△EFM;∴DM=EM;
类型四、旋转模型
例.如图1,,,,、相交于点,连接.
(1)求证:,并用含的式子表示的度数;
(2)当时,取,的中点分别为点、,连接,,,如图2,判断的形状,并加以证明.
【答案】(1)证明见解析;;(2)为等腰直角三角形;证明见解析.
【详解】证明:(1)如图1,,
,,
在和中,,,;
,,
中,,,
,
中,;即;
(2)为等腰直角三角形.证明:如图2,由(1)可得,,
,的中点分别为点、,,
,,
在和中,,,
,且,
又,,,为等腰直角三角形.
【变式训练1】四边形是由等边和顶角为的等腰排成,将一个角顶点放在处,将角绕点旋转,该交两边分别交直线、于、,交直线于、两点.
(1)当、都在线段上时(如图1),请证明:;
(2)当点在边的延长线上时(如图2),请你写出线段,和之间的数量关系,并证明你的结论;
(3)在(1)的条件下,若,,请直接写出的长为 .
【答案】(1)证明见解析;(2).证明见解析;(3).
【解析】解:(1)证明:把△DBM绕点D逆时针旋转120°得到△DAQ,
则DM=DQ,AQ=BM,∠ADQ=∠BDM,∠QAD=∠CBD=90°,
∴点Q在直线CA上,
∵∠QDN=∠ADQ+∠ADN=∠BDM+∠ADN=∠ABD-∠MDN=120°-60°=60°,∴∠QDN=∠MDN=60°,
∵在△MND和△QND中,,∴△MND≌△QND(SAS),∴MN=QN,
∵QN=AQ+AN=BM+AN,∴BM+AN=MN;
(2):.理由如下:如图,把△DAN绕点D顺时针旋转120°得到△DBP,
则DN=DP,AN=BP,
∵∠DAN=∠DBP=90°,∴点P在BM上,
∵∠MDP=∠ADB-∠ADM-∠BDP=120°-∠ADM-∠ADN=120°-∠MDN=120°-60°=60°,∴∠MDP=∠MDN=60°,
∵在△MND和△MPD中,,∴△MND≌△MPD(SAS),∴MN=MP,
∵BM=MP+BP,∴MN+AN=BM;
(3)如图,过点M作MH∥AC交AB于G,交DN于H,
∵△ABC是等边三角形,∴△BMG是等边三角形,∴BM=MG=BG,
根据(1)△MND≌△QND可得∠QND=∠MND,
根据MH∥AC可得∠QND=∠MHN,∴∠MND=∠MHN,
∴MN=MH,∴GH=MH-MG=MN-BM=AN,即AN=GH,
∵在△ANE和△GHE中,,∴△ANE≌△GHE(AAS),∴AE=EG=2.1,
∵AC=7,∴AB=AC=7,∴BG=AB-AE-EG=7-2.1-2.1=2.8,∴BM=BG=2.8.故答案为:2.8
【变式训练2】(1)问题发现:
如图1,△ACB和△DCE均为等边三角形,当△DCE旋转至点A,D,E在同一直线上,连接BE.则:
①∠AEB的度数为 °;
②线段AD、BE之间的数量关系是 .
(2)拓展研究:
如图2,△ACB和△DCE均为等腰三角形,且∠ACB=∠DCE=90°,点 A、D、E在同一直线上,若AD=a,AE=b,AB=c,求a、b、c之间的数量关系.
(3)探究发现:
图1中的△ACB和△DCE,在△DCE旋转过程中,当点A,D,E不在同一直线上时,设直线AD与BE相交于点O,试在备用图中探索∠AOE的度数,直接写出结果,不必说明理由.
【答案】(1)①60;②AD=BE;(2)a2+b2=c2;(3)60°或120°
【详解】解:(1)①如图1,∵△ACB和△DCE均为等边三角形,
∴CA=CB,CD=CE,∠ACB=∠DCE=60°,∴∠ACD=∠BCE,
在△ACD和△BCE中,,∴△ACD≌△BCE(SAS).∴∠ADC=∠BEC.
∵△DCE为等边三角形,∴∠CDE=∠CED=60°,
∵点A,D,E在同一直线上,∴∠ADC=120°,∴∠BEC=120°,∴∠AEB=∠BEC-∠CED=60°,
故答案为:60;
②∵△ACD≌△BCE,∴AD=BE,故答案为:AD=BE;
(2)∵△ACB和△DCE均为等腰直角三角形,
∴CA=CB,CD=CE,∠ACB=∠DCE=90°.
∴∠ACD=∠BCE,∴△ACD≌△BCE(SAS),
∴BE=AD,∠ADC=∠BEC,
∵△DCE为等腰直角三角形,∴∠CDE=∠CED=45°.
∵点A,D,E在同一直线上,
∴∠ADC=135°.∴∠BEC=135°,
∴∠AEB=∠BEC-∠CED=90°,∴AD2+AE2=AB2,
∵AD=a,AE=b,AB=c,∴a2+b2=c2;
(3)如图3,
由(1)知△ACD≌△BCE,
∴∠CAD=∠CBE,
∵∠CAB=∠CBA=60°,
∴∠OAB+∠OBA=120°,
∴∠AOE=180°-120°=60°,
如图4,
同理求得∠AOB=60°,
∴∠AOE=120°,
∴∠AOE的度数是60°或120°.
【变式训练3】如图1,在中,,,点,分别在边,上,,连接,点,,分别为,,的中点.
(1)观察猜想:图1中,线段与的数量关系是______,位置关系是______.
(2)探究证明:把绕点逆时针方向旋转到图2的位置,连接,,,判断的形状,并说明理由;
(3)拓展延伸:把绕点在平面内自由旋转,若,,请直接写出面积的最大值.
【答案】(1)、;(2)等腰直角三角形,证明见解析;(3)
【详解】解:(1)∵点P,N是BC,CD的中点, ∴PN∥BD,PN=BD,
∵点P,M是CD,DE的中点, ∴PM∥CE,PM=CE,
∵AB=AC,AD=AE, ∴BD=CE, ∴PM=PN,
∵PN∥BD, ∴∠DPN=∠ADC,
∵PM∥CE, ∴∠DPM=∠DCA,
∵∠BAC=90°, ∴∠ADC+∠ACD=90°, ∴∠MPN=∠DPM+∠DPN=∠DCA+∠ADC=90°,
∴PM⊥PN, 故答案为:PM=PN,PM⊥PN;
(2)△PMN是等腰直角三角形. 理由如下: 由旋转知,∠BAD=∠CAE,
∵AB=AC,AD=AE, ∴△ABD≌△ACE(SAS), ∴∠ABD=∠ACE,BD=CE,
利用三角形的中位线得,PN=BD,PM=CE, ∴PM=PN, ∴△PMN是等腰三角形,
同(1)的方法得,PM∥CE, ∴∠DPM=∠DCE, 同(1)的方法得,PN∥BD,
∴∠PNC=∠DBC,
∵∠DPN=∠DCB+∠PNC=∠DCB+∠DBC,
∴∠MPN=∠DPM+∠DPN=∠DCE+∠DCB+∠DBC =∠BCE+∠DBC=∠ACB+∠ACE+∠DBC =∠ACB+∠ABD+∠DBC=∠ACB+∠ABC,
∵∠BAC=90°, ∴∠ACB+∠ABC=90°, ∴∠MPN=90°, ∴△PMN是等腰直角三角形;
(3)由(2)知,△PMN是等腰直角三角形,PM=PN=BD,
∴PM最大时,△PMN面积最大, ∴点D在BA的延长线上, ∴BD=AB+AD=14, ∴PM=7,
∴S△PMN最大= PM2=×49=.
类型五、手拉手模型
例.在等边中,点D在AB上,点E在BC上,将线段DE绕点D逆时针旋转60°得到线段DF,连接CF.
(1)如图(1),点D是AB的中点,点E与点C重合,连接AF.若,求AF的长;
(2)如图(2),点G在AC上且,求证:;
(3)如图(3),,,连接AF.过点F作AF的垂线交AC于点P,连接BP、DP.将沿着BP翻折得到,连接QC.当的周长最小时,直接写出的面积.
【答案】(1)AF=3;(2)见解析;(3),详见解析
【解析】(1)解:∵△ABC为等边三角形,∴BC=AC,∠BCA=60°,
由旋转知,∠CDF=60°,CD=CF,∴△DCF为等边三角形,∴CD=CF,∠DCF=60°,
∴∠DCB=∠ACF,∴△BCD≌△ACF,∴AF=BD,
∵D为AB中点,AB=6,∴BD=3,∴AF=3.
(2)解:将CF绕C顺时针旋转60°得CH,连接CH,FH,EF,EH,CD,
在AC上截取AP=BE,连接DP,设CD交EH于M,
如图所示,
由旋转知,△DEF、△CFH为等边三角形,
∴DF=EF,CF=FH,∠DFE=∠CFH=60°,∴∠DFC=∠EFH,∴△DCF≌△BHF,
∴EH=CD,∠DCF=∠EHF,
由三角形内角和知,∠HMC+∠EHF=∠DCF+∠HFC,
∴∠HMC=∠HFC=60°,∴∠DCE+∠HEC=60°,
∵∠DCP+∠DCE=60°, ∴∠CEH=∠DCP,
∵AC=BC,AP=BE,∴CP=CE,∴△ECH≌△CPD,∴CH=DP,∠DPC=∠HCE,
又∠HCE=60°+∠2,∴∠DPC=60°+∠2,
由∠1+∠FCG=∠2+∠FCG=60°,知∠1=∠2,又∠AGD=60°+∠1,∴∠AGD=∠DPG, ∴DP=DG,
∵CH=CF,∴CF=DG.
(3):过D作DH⊥CB于H,连接EF,如图所示,
∵△ABC为等边三角形,∴∠DBH=60°,∠BDH=30°,
∴BD=2BH,DH=,
∵BD=2CE,∴BH=CE,
设BH=CE=x,则BD=2x,EH=6-2x,AD=6-2x,
由旋转知,△DEF为等边三角形,∠EDF=60°,∴∠1+∠3=90°,DE=DF,
又∠1+∠2=90°,∴∠2=∠3,∴△ADF≌△HED,
∴∠DAF=∠DHE=90°,∠PAF=30°,AF=DH=,
∵∠AFP=90°,∴PF=x,AP=2x,
过P作PM⊥AD于M,则AM=x,DM=6-3x,PM=,
在Rt△PDM中,由勾股定理得:PD=,
故△ADP周长=AD+AP+PD=6-2x+2x+=6+,
∴当x=时,周长取最小值,最小值为9,此时DP=3,
∴BD=AP=3,即D为AB中点,P为AC中点,
∴直线BP是等边△ABC对称轴,
如图所示,△BDP沿BP折叠后,Q点落在BC中点处,
则△PCQ面积=×△ABC面积=××=.
【变式训练1】△ACB和△DCE是共顶点C的两个大小不一样的等边三角形.
(1)问题发现:
如图1,若点A,D,E在同一直线上,连接AE,BE.
①求证:△ACD≌△BCE;
②求∠AEB的度数.
(2)类比探究:如图2,点B、D、E在同一直线上,连接AE,AD,BE,CM为△DCE中DE边上的高,请求∠ADB的度数及线段DB,AD,DM之间的数量关系,并说明理由.
(3)拓展延伸:如图3,若设AD(或其延长线)与BE的所夹锐角为α,则你认为α为多少度,并证明.
【答案】(1)①见解析;②∠AEB=60°;(2)∠ADB=60°,2DM+BD=AD,理由见解析;(3)α=60°,证明见解析
【解析】(1)①证明:∵△ACB和△DCE是等边三角形,
∴AC=BC,CD=CE,∠ACB=∠DCE=60°,
∴∠ACD=60°-∠DCB=∠BCE,
∴△ACD≌△BCE(SAS);
②∵△ACD≌△BCE,
∴∠ADC=∠BEC=180°-∠CDE=120°,
又∵∠CED=60°,
∴∠AEB=60°;
(2)解:∠ADB=60°,2DM +BD=AD,理由如下;
∵AC=BC,CD=CE,∠ACD=60°+∠DCB=∠BCE,
∴△ACD≌△BCE(SAS),
∴∠CDA=∠CED=60°;
∵∠ADB+∠CDA=∠DCE+∠CED,
∴∠ADB=60°;
又∵CM⊥BE,且△CDE为等边三角形,
∴DE=2DM,
∴2DM +BD=BE=AD;
(3)解:α=60°,理由如下:
同理可证△ACD≌△BCE,
∴∠BEC=∠ADC,
∴∠CDF+∠CEF=180°,
∴∠ECD+∠DFE=180°,
而α+∠DFE=180°,
∴α=∠ECD=60°.
【变式训练2】(1)如图1,锐角△ABC中,分别以AB、AC为边向外作等腰直角△ABE和等腰直角△ACD,使AE=AB,AD=AC,∠BAE=∠CAD=90°,连接BD,CE,试猜想BD与CE的大小关系,不需要证明.
【深入探究】(2)如图2,四边形ABCD中,AB=5,BC=2,∠ABC=∠ACD=∠ADC=45°,求BD2的值;甲同学受到第一问的启发构造了如图所示的一个和△ABD全等的三角形,将BD进行转化再计算,请你准确的叙述辅助线的作法,再计算;
【变式思考】(3)如图3,四边形ABCD中,AB=BC,∠ABC=60°,∠ADC=30°,AD=6,BD=10,则CD= .
【答案】(1)BD=CE;(2)BD2=54;(3)8
【详解】解:(1)BD=CE.理由是:
∵∠BAE=∠CAD, ∴∠BAE+∠BAC=∠CAD+∠BAC,即∠EAC=∠BAD,
在△EAC和△BAD中, ,
∴△EAC≌△BAD, ∴BD=CE;
(2)如图2,在△ABC的外部,以A为直角顶点作等腰直角△BAE,使∠BAE=90°,AE=AB,连接EA、EB、EC.
∵∠ACD=∠ADC=45°, ∴AC=AD,∠CAD=90°,
∴∠BAE+∠BAC=∠CAD+∠BAC,即∠EAC=∠BAD,
在△EAC和△BAD中,
,
∴△EAC≌△BAD,
∴BD=CE.
∵AE=AB=5,
∴BE=,∠ABE=∠AEB=45°,
又∵∠ABC=45°,
∴∠ABC+∠ABE=45°+45°=90°,
∴,
∴ .
(3)如图,
∵AB=BC,∠ABC=60°,∴△ABC是等边三角形,
把△ACD绕点C逆时针旋转60°得到△BCE,连接DE,
则BE=AD,△CDE是等边三角形,
∴DE=CD,∠CED=60°,
∵∠ADC=30°,
∴∠BED=30°+60°=90°,
在Rt△BDE中,DE===8,
∴CD=DE=8.
【变式训练3】(1)问题发现:
如图1,和均为等腰直角三角形,,连接,,点、、在同一条直线上,则的度数为__________,线段、之间的数量关系__________;
(2)拓展探究:
如图2,和均为等腰直角三角形,,连接,,点、、不在一条直线上,请判断线段、之间的数量关系和位置关系,并说明理由.
(3)解决问题:
如图3,和均为等腰三角形,,则直线和的夹角为__________.(请用含的式子表示)
【答案】(1)90°,AD=BE;(2)AD=BE,AD⊥BE;(3)
【详解】(1)∵和均为等腰直角三角形,,
∴,,∠CDE=45°∴∠CDA=135°
∵∠ACB−∠DCB=∠DCE−∠DCB,∴∠ACD=∠BCE.
在△ACD和△BCE中,,
∴△ACD≌△BCE(SAS),
∴∠BEC=∠ADC=135°,AD=BE,∴∠AEB=90°
故答案为:90°,AD=BE
AD=BE,AD⊥BE,理由如下,
同理可得△ACD≌△BCE,则AD=BE,
延长交于点F,
设∠FAB=α,则∠CAD=∠CBE=45°-α
∴∠ABE=45°+45°-α=90°-α
∴∠AFB=180°-∠FAB-∠ABE=180°-α-(90°-α)=90°
∴AD⊥BE
(3)如图,延长BE交AD于点G,
∵和均为等腰三角形,∴,,
∵∠ACB=∠DCE=α,
∵∠ACB+∠ACE=∠DCE+∠ACE,∴∠ACD=∠BCE.
在△ACD和△BCE中,
,∴△ACD≌△BCE(SAS),∴∠CBE=∠CAD
∵,∴∠CBA=∠CAB =
∴∠GAB+∠GBA=,
∴∠AGB=180°-(∠GAB+∠GBA) ,即直线和的夹角为.
故答案为:.
类型六、一线三角模型
例.在中,,,直线MN经过点C且于D,于E.
(1)当直线MN绕点C旋转到图1的位置时,求证:
①≌;
②;
(2)当直线MN烧点C旋转到图2的位置时,求证:;
(3)当直线MN绕点C旋转到图3的位置时,试问DE、AD、BE具有怎样的等量关系?请写出这个等量关系,并加以证明.
【答案】(1)①证明见解析;②证明见解析;(2)证明见解析
(3)(或者对其恒等变形得到,),证明见解析
【解析】(1)解:①,,,
,,,
在和中,;
②,,,;
(2)证明:,,,,
在和中,;,,
;
(3)证明:当旋转到题图(3)的位置时,,,所满足的等量关系是:或或.
理由如下:,,
,
,
在和中,
,
,,
(或者对其恒等变形得到或).
【变式训练1】【问题解决】
(1)已知△ABC中,AB=AC,D,A,E三点都在直线l上,且有∠BDA=∠AEC=∠BAC.如图①,当∠BAC=90°时,线段DE,BD,CE的数量关系为:______________;
【类比探究】
(2)如图②,在(1)的条件下,当0°<∠BAC<180°时,线段DE,BD,CE的数量关系是否变化,若不变,请证明:若变化,写出它们的关系式;
【拓展应用】
(3)如图③,AC=BC,∠ACB=90°,点C的坐标为(-2,0),点B的坐标为(1,2),请求出点A的坐标.
【答案】(1)DE=BD+CE;(2)DE=BD+CE的数量关系不变,理由见解析;(3)(﹣4,3)
【解析】解:(1)∵∠BAC=90°,∴∠BDA=∠AEC=∠BAC=90°,
∴∠ABD+∠BAD=90°,∠CAE+∠BAD=90°,∴∠ABD=∠CAE,
在△ABD和△CAE中,,∴△ABD≌△CAE(AAS),∴AD=CE,BD=AE,
∴DE=AD+AE=BD+CE,故答案为:DE=BD+CE;
(2)DE=BD+CE的数量关系不变,理由如下:∵∠BAE是△ABD的一个外角,
∴∠BAE=∠ADB+∠ABD,
∵∠BDA=∠BAC,∴∠ABD=∠CAE,
在△ABD和△CAE中,,∴△ABD≌△CAE(AAS),
∴AD=CE,BD=AE,∴DE=AD+AE=BD+CE;
(3)过点A作AM⊥x轴于点M,过点B作BN⊥x轴于点N,
∵点C的坐标为(﹣2,0),点B的坐标为(1,2),
∴OC=2,ON=1,BN=2,∴CN=3,
由(1)可知,△ACM≌△CBN,
∴AM=CN=3,CM=BN=2,
∴OM=OC+CM=4,
∴点A的坐标为(﹣4,3).
【变式训练2】(1)如图1,在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D、E.求证:△ABD≌△CAE;
(2)如图2,将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意锐角或钝角.请问结论△ABD≌△CAE是否成立?如成立,请给出证明;若不成立,请说明理由.
(3)拓展应用:如图3,D,E是D,A,E三点所在直线m上的两动点(D,A,E三点互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD,CE,若∠BDA=∠AEC=∠BAC,求证:△DEF是等边三角形.
【答案】(1)见详解;(2)成立,理由见详解;(3)见详解
【详解】(1)证明:直线,直线,
,
,,
,
,
在和中,,;
解:(2)成立,理由如下:
,,
,
在和中,,;
(3)证明:∵△ABF和△ACF均为等边三角形,
∴,
∴∠BDA=∠AEC=∠BAC=120°,
∴,
∴,
∴,
∴,
∵,
∴,
∴(SAS),
∴,
∴,
∴△DFE是等边三角形.
【变式训练3】探究:(1)如图(1),已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D、E.请直接写出线段BD,DE,CE之间的数量关系是 .
拓展:(2)如图(2),将探究中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意锐角或钝角.请问探究中的结论是否成立?如成立,请你给出证明;若不成立,请说明理由.
应用:(3)如图(3),D、E是D、A、E三点所在直线m上的两动点(D、A、E三点互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD、CE,若∠BDA=∠AEC=∠BAC,请直接写出△DEF的形状是 .
【答案】探究:(1)DE=BD+CE;拓展:(1)成立,见解析;应用:(3)△DEF是等边三角形
【解析】(1)解:如图1,
∵BD⊥直线m,CE⊥直线m,
∴∠BDA=∠CEA=90°,
∵∠BAC=90°,
∴∠BAD+∠CAE=90°
∵∠BAD+∠ABD=90°,
∴∠CAE=∠ABD,
在△ADB和△CEA中,
,
∴△ADB≌△CEA(AAS),
∴AE=BD,AD=CE,
∴DE=AE+AD=BD+CE;
故答案为:DE=BD+CE
(2)解:如图2,
∵∠BDA=∠BAC=α,
∴∠DBA+∠BAD=∠BAD+∠CAE=180°﹣α,
∴∠DBA=∠CAE,
在△ADB和△CEA中,
,
∴△ADB≌△CEA(AAS),
∴AE=BD,AD=CE,
∴DE=AE+AD=BD+CE;
(3)证明:如图3,
由(2)可知,△ADB≌△CEA,
∴BD=AE,∠DBA=∠CAE,
∵△ABF和△ACF均为等边三角形,
∴∠ABF=∠CAF=60°,BF=AF,
∴∠DBA+∠ABF=∠CAE+∠CAF,
∴∠DBF=∠FAE,
∵在△DBF和△EAF中,
,
∴△DBF≌△EAF(SAS),
∴DF=EF,∠BFD=∠AFE,
∴∠DFE=∠DFA+∠AFE=∠DFA+∠BFD=60°,
∴△DEF为等边三角形.
沪教版八年级数学下册期中期末满分冲刺卷专题02全等三角形中的六种模型梳理(原卷版+解析): 这是一份沪教版八年级数学下册期中期末满分冲刺卷专题02全等三角形中的六种模型梳理(原卷版+解析),共51页。试卷主要包含了倍长中线模型,截长补短模型,做平行线证明全等,旋转模型,手拉手模型,一线三角模型等内容,欢迎下载使用。
人教版八年级数学上册同步精品压轴题专题07因式分解的六种方法大全(学生版+解析): 这是一份人教版八年级数学上册同步精品压轴题专题07因式分解的六种方法大全(学生版+解析),共20页。试卷主要包含了提取公因式法与公式法综合,十字相乘法,分组法,换元法,主元法等内容,欢迎下载使用。
人教版八年级数学上册同步精品压轴题专题02全等三角形中的六种模型梳理(学生版+解析): 这是一份人教版八年级数学上册同步精品压轴题专题02全等三角形中的六种模型梳理(学生版+解析),共53页。试卷主要包含了倍长中线模型,截长补短模型,做平行线证明全等,旋转模型,手拉手模型,一线三角模型等内容,欢迎下载使用。












