专题一　培优点3　同构函数问题--高三高考数学复习-PPT

这是一份专题一　培优点3　同构函数问题--高三高考数学复习-PPT，共60页。PPT课件主要包含了内容索引，考点一，考点二，双变量同构问题，指对同构问题，专题强化练，规律方法，e＋∞等内容，欢迎下载使用。

同构函数问题，是近几年高考的热点问题，考查数学素养和创新思维.同构函数问题是指在不等式、方程、函数中，通过等价变形形成相同形式，再构造函数，利用函数的性质解决问题，常见的同构有双变量同构和指对同构，一般都是压轴题，难度较大.
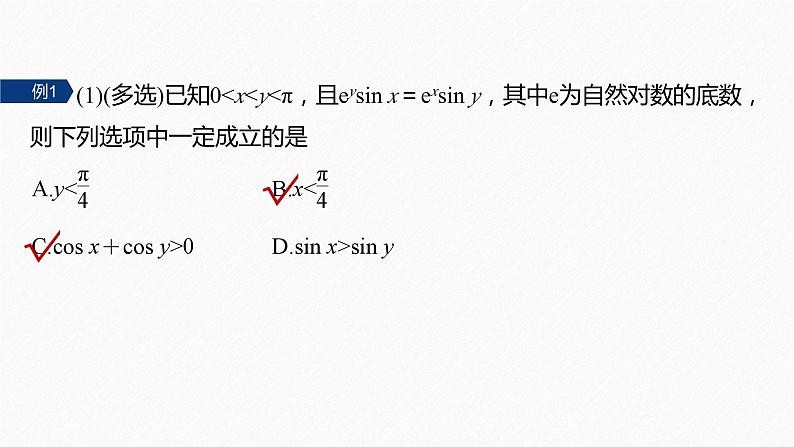
　　(1)(多选)已知0(2)(2023·大连模拟)若实数a，b满足4a＋lg3a＝8b＋3lg27b，则
由题意知a>0，b>0，∵4a＝22a,8b＝23b,3lg27b＝lg3b，∴22a＋lg3a＝23b＋lg3b，∴22a＋lg3a＋lg32＝23b＋lg3b＋lg32，即22a＋lg32a＝23b＋lg32b，∵y＝lg3x在(0，＋∞)上单调递增，∴lg32b∵y＝2x与y＝lg3x在(0，＋∞)上单调递增，∴f(x)在(0，＋∞)上单调递增，
含有地位相等的两个变量的不等式(方程)，关键在于对不等式(方程)两边变形或先放缩再变形，使不等式(方程)两边具有结构的一致性，再构造函数，利用函数的性质解决问题.
　　　(1)若对于0∵x2ln x1－x1ln x2≤x1－x2，
又0当x∈(0,1)时，φ′(x)>0，当x∈(1，＋∞)时，φ′(x)<0，∴φ(x)在(0,1)上单调递增，在(1，＋∞)上单调递减，故a≤1，∴a的最大值为1.
(2)(2023·德阳模拟)已知实数x，y满足eyln x＝yex，y>1，则x，y的大小关系为A.y≥x B.yx D.y≤x
令f(x)＝x－ln x，
当x>1时，f′(x)>0，
所以函数f(x)在(1，＋∞)上单调递增，则当x>1时，f(x)>f(1)，即x－ln x>1，一定有x－ln x>0，
当x>1时，g′(x)>0，所以函数g(x)在(1，＋∞)上单调递增，
考向1　指对同构与恒成立问题
　已知函数f(x)＝ex＋(1－a)x－ln ax(a>0).(1)当a＝1时，求曲线y＝f(x)在点(1，f(1))处的切线方程；
当a＝1时，f(x)＝ex－ln x，
切点坐标为(1，e)，斜率为f′(1)＝e－1，所求切线方程为y－e＝(e－1)(x－1)，即(e－1)x－y＋1＝0.
(2)若对于任意的x>0，有f(x)≥0，求正数a的取值范围.
f(x)≥0，即ex＋x－ax－ln ax≥0(a>0，x>0)⇔ex＋x≥ax＋ln ax(a>0，x>0)⇔ex＋x≥eln ax＋ln ax(a>0，x>0).令g(x)＝ex＋x，显然g(x)是增函数，于是上式可化为g(x)≥g(ln ax)，即x≥ln ax(a>0，x>0)⇔ln a≤x－ln x(a>0，x>0).令φ(x)＝x－ln x(x>0)，
易知φ(x)在(0,1)上单调递减，在(1，＋∞)上单调递增，故φ(x)min＝φ(1)＝1，于是ln a≤1，可得0考向2　指对同构与证明不等式
　已知函数f(x)＝xln x.(1)求f(x)的最小值；
f(x)的定义域为(0，＋∞)，f′(x)＝1＋ln x，
∵x>2，∴x－1>1，
即证xex>(x－1)ln(x－1)，即证exln ex>(x－1)ln(x－1)，即证f(ex)>f(x－1)，
令φ(x)＝ex－(x－1)(x>2)，φ′(x)＝ex－1>0，φ(x)在(2，＋∞)上单调递增，∴φ(x)>φ(2)＝e2－1>0，∴ex>x－1，即证原不等式成立.
指对同构的常用形式(1)积型：aea≤bln b，一般有三种同构方式：①同左构造形式：aea≤ln beln b，构造函数f(x)＝xex；②同右构造形式：ealn ea≤bln b，构造函数f(x)＝xln x；③取对构造形式：a＋ln a≤ln b＋ln(ln b) (b>1)，构造函数f(x)＝x＋ln x.
(3)和、差型：ea±a>b±ln b，一般有两种同构方式：①同左构造形式：ea±a>eln b±ln b，构造函数f(x)＝ex±x；②同右构造形式：ea±ln ea>b±ln b，构造函数f(x)＝x±ln x.
　　　已知a>0，函数f(x)＝xex－ax.(1)当a＝1时，求曲线y＝f(x)在x＝1处的切线方程；
当a＝1时，f(x)＝xex－x，所以f′(x)＝(x＋1)ex－1，所以f′(1)＝2e－1，f(1)＝e－1，所以切线方程为y－(e－1)＝(2e－1)(x－1)，即(2e－1)x－y－e＝0.
(2)若f(x)≥ln x－x＋1恒成立，求实数a的取值范围.
由题意得xex－ax≥ln x－x＋1，即xex－ln x＋x－1≥ax，
令t＝x＋ln x，易知t＝x＋ln x在(0，＋∞)上单调递增，当x→0时，t→－∞，当x→＋∞时，t→＋∞，
所以存在x0，使t＝x0＋ln x0＝0，令m(t)＝et－t－1，t∈R，因为m′(t)＝et－1，所以当t∈(－∞，0)时，m′(t)<0，即m(t)在(－∞，0)上单调递减；当t∈(0，＋∞)时，m′(t)>0，即m(t)在(0，＋∞)上单调递增，所以m(t)min＝m(0)＝0，所以m(t)≥m(0)＝0，
即m(t)＝et－t－1≥0，得到et≥t＋1，当且仅当t＝0时取等号，
当且仅当x＋ln x＝0时取等号，所以a≤2，又a>0，所以a的取值范围是(0,2].
1.(2023·南宁模拟)已知α，β∈R，则“α＋β>0”是“α＋β>cs α－cs β”的A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件
构造函数f(x)＝x－cs x，则f′(x)＝1＋sin x≥0在定义域R上恒成立，所以函数f(x)＝x－cs x为增函数，又因为α＋β>0，所以α>－β，所以f(α)>f(－β)，即α－cs α>－β－cs(－β)，即α－cs α>－β－cs β，所以α＋β>cs α－cs β，即“α＋β>0”能推出“α＋β>cs α－cs β”；
根据α＋β>cs α－cs β，可得α－cs α>－β－cs β，即α－cs α>－β－cs(－β)，所以f(α)>f(－β)，所以α>－β，即α＋β>0，所以“α＋β>cs α－cs β”能推出“α＋β>0”，所以“α＋β>0”是“α＋β>cs α－cs β”的充要条件.
2.已知x∈N，y∈N，xxy＝yx，两边取对数，得yln x＝xln y，
当x∈(0，e)时，f′(x)>0，f(x)单调递增，当x∈(e，＋∞)时，f′(x)<0，f(x)单调递减，且当x∈(0,1]时，f(x)≤0，
所以满足x∈N，y∈N，x3.若2a＋lg2a＝4b＋2lg4b，则A.a>2b B.a<2bC.a>b2 D.a由指数和对数的运算性质可得2a＋lg2a＝4b＋2lg4b＝22b＋lg2b.令f(x)＝2x＋lg2x，则f(x)在(0，＋∞)上单调递增，又∵22b＋lg2b<22b＋lg2b＋1＝22b＋lg22b，∴2a＋lg2a<22b＋lg22b，即f(a)4.设a，b都为正数，e为自然对数的底数，若aeae B.b>eaC.ab由已知aea0，∴ea>1，∵b>0，bln b>aea>0，∴b>1.当x>1时，f′(x)＝ln x＋1>0，则f(x)在(1，＋∞)上单调递增，所以ea5.(多选)已知a>b>1，若ea－2a＝aeb＋1－bea，则A.ln(a－b)<0B.ln(a＋b)>1C.3a＋3－b>D.3a－1<3b
由ea－2a＝aeb＋1－bea，得(b＋1)ea＝a(eb＋1＋2)，
所以f(x)在(1，＋∞)上单调递增.
所以f(a)>f(b＋1)，所以a>b＋1，所以a－b>1，所以ln(a－b)>ln 1＝0，A错误；因为a＋b>b＋1＋b>3>e，所以ln(a＋b)>ln e＝1，B正确；
因为a－1>b，所以3a－1>3b，D错误.
6.若f(x)＝xex－a(x＋ln x)有两个零点，则实数a的取值范围是__________.
f(x)＝xex－a(x＋ln x)＝ex＋ln x－a(x＋ln x)，令t＝x＋ln x，t∈R，显然该函数为增函数.
(1)讨论函数g(x)在定义域内的单调性；
由g′(x)>0，得0e.∴g(x)在(0，e)上单调递增，在(e，＋∞)上单调递减.
(2)若f(x)≥g(x)恒成立，求实数a的取值范围.
得a≤xex＋1－ln x－x＝eln x＋x＋1－(ln x＋x＋1)＋1，令t＝ln x＋x＋1，t∈R，即a≤et－t＋1恒成立，令φ(t)＝et－t＋1，t∈R，则φ′(t)＝et－1，当t∈(－∞，0)时，φ′(t)<0；当t∈(0，＋∞)时，φ′(t)>0，∴φ(t)在(－∞，0)上单调递减，在(0，＋∞)上单调递增，∴φ(t)min＝φ(0)＝2，故a≤2.
8.(2023·潍坊模拟)已知函数f(x)＝ex－1ln x，g(x)＝x2－x.(1)讨论f(x)的单调性；
函数f(x)的定义域为(0，＋∞)，
所以当01时，h′(x)>0，函数h(x)单调递增，
所以h(x)≥h(1)＝1，
所以函数f(x)在(0，＋∞)上单调递增.
(2)证明：当x∈(0,2)时，f(x)≤g(x).
原不等式为ex－1ln x≤x2－x＝x(x－1)，
所以当x<1时，φ′(x)>0，φ(x)单调递增，
令t(x)＝ln x－x＋1，x∈(0,2)，
当00，t(x)单调递增；当1所以可得到φ(ln x)≤φ(x－1)，
所以当x∈(0,2)时，有f(x)≤g(x)成立.