

2024年中考数学压轴题之学霸秘笈大揭秘专题18二次函数与旋转变换综合问题(原卷版+解析)
展开【例1】 (2023•凉山州)在平面直角坐标系xOy中,已知抛物线y=﹣x2+bx+c经过点A(﹣1,0)和点B(0,3),顶点为C,点D在其对称轴上,且位于点C下方,将线段DC绕点D按顺时针方向旋转90°,点C落在抛物线上的点P处.
(1)求抛物线的解析式;
(2)求点P的坐标;
(3)将抛物线平移,使其顶点落在原点O,这时点P落在点E的位置,在y轴上是否存在点M,使得MP+ME的值最小,若存在,求出点M的坐标;若不存在,请说明理由.
【例2】. (2023•梧州)如图,在平面直角坐标系中,直线y=﹣x﹣4分别与x,y轴交于点A,B,抛物线y=x2+bx+c恰好经过这两点.
(1)求此抛物线的解析式;
(2)若点C的坐标是(0,6),将△ACO绕着点C逆时针旋转90°得到△ECF,点A的对应点是点E.
①写出点E的坐标,并判断点E是否在此抛物线上;
②若点P是y轴上的任一点,求BP+EP取最小值时,点P的坐标.
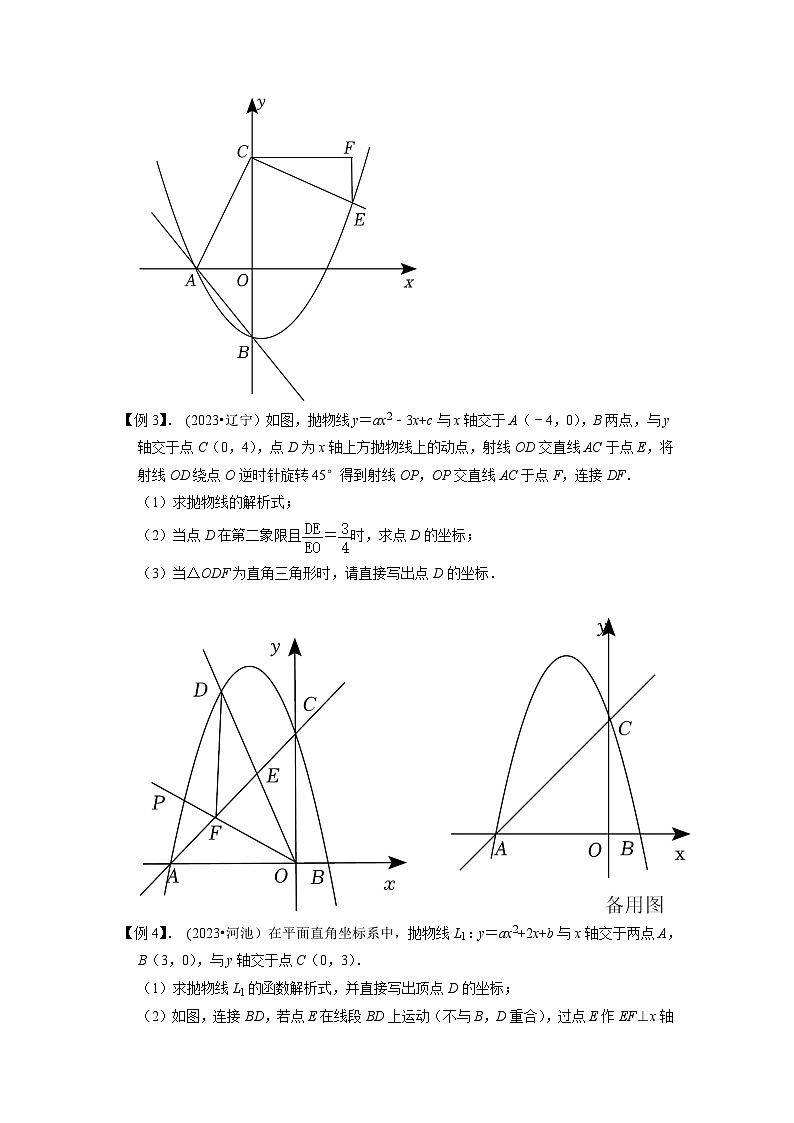
【例3】. (2023•辽宁)如图,抛物线y=ax2﹣3x+c与x轴交于A(﹣4,0),B两点,与y轴交于点C(0,4),点D为x轴上方抛物线上的动点,射线OD交直线AC于点E,将射线OD绕点O逆时针旋转45°得到射线OP,OP交直线AC于点F,连接DF.
(1)求抛物线的解析式;
(2)当点D在第二象限且=时,求点D的坐标;
(3)当△ODF为直角三角形时,请直接写出点D的坐标.
【例4】. (2023•河池)在平面直角坐标系中,抛物线L1:y=ax2+2x+b与x轴交于两点A,B(3,0),与y轴交于点C(0,3).
(1)求抛物线L1的函数解析式,并直接写出顶点D的坐标;
(2)如图,连接BD,若点E在线段BD上运动(不与B,D重合),过点E作EF⊥x轴于点F,设EF=m,问:当m为何值时,△BFE与△DEC的面积之和最小;
(3)若将抛物线L1绕点B旋转180°得抛物线L2,其中C,D两点的对称点分别记作M,N.问:在抛物线L2的对称轴上是否存在点P,使得以B,M,P为顶点的三角形为等腰三角形?若存在,直接写出所有符合条件的点P的坐标;若不存在,请说明理由.
一.解答题(共20小题)
1. (2023•碑林区校级三模)如图,在平面直角坐标系中,抛物线W1与x轴交于A,B两点,与y轴交于点C(0,﹣6),顶点为D(﹣2,2).
(1)求抛物线W1的表达式;
(2)将抛物线W1绕原点O旋转180°得到抛物线W2,抛物线W2的顶点为D′,在抛物线W2上是否存在点M,使S△D′AD=S△D′DM?若存在,请求出点M的坐标;若不存在,请说明理由.
2. (2023•双流区模拟)如图,抛物线C:y=ax2+6ax+9a﹣8与x轴相交于A,B两点(点A在点B的左侧),已知点B的横坐标是2,抛物线C的顶点为D.
(1)求a的值及顶点D的坐标;
(2)点P是x轴正半轴上一点,将抛物线C绕点P旋转180°后得到抛物线C1,记抛物线C1的顶点为E,抛物线C1与x轴的交点为F,G(点F在点G的右侧).当点P与点B重合时(如图1),求抛物线C1的表达式;
(3)如图2,在(2)的条件下,从A,B,D中任取一点,E,F,G中任取两点,若以取出的三点为顶点能构成直角三角形,我们就称抛物线C1为抛物线C的“勾股伴随同类函数”.当抛物线C1是抛物线C的勾股伴随同类函数时,求点P的坐标.
3. (2023•灞桥区校级模拟)已知:如图,在平面直角坐标系xOy中,直线y=x+6与x轴、y轴的交点分别为A、B,其中点C是x轴上一点,OC=3.
(1)求过A、B、C三点的抛物线L的解析式;
(2)将抛物线L绕着点O旋转180°得到抛物线L1,抛物线L1与x轴交于F点、E点(点F在点E的左侧),与y轴交于点M,则抛物线L1的对称轴上是否存在一点Q,使|QF﹣QM|的值最大?若存在,求出点Q的坐标及其最大值,若不存在,请说明理由.
4. (2023•莲湖区二模)已知抛物线W1:y=ax2﹣bx﹣3与x轴交于A(﹣1,0)、B(3,0)两点与y轴交于点C,顶点为D.
(1)求抛物线W1的表达式;
(2)将抛物线W1绕原点O旋转180°后得到抛物线W2,W2的顶点为D',点M为W2上的一点,当△D'DM的面积等于△ABC的面积时,求点M的坐标.
5. (2023•深圳三模)已知抛物线y=ax2+c过点A(﹣2,0)和D(﹣1,3)两点,交x轴于另一点B.
(1)求抛物线解析式;
(2)如图1,点P是BD上方抛物线上一点,连接AD,BD,PD,当BD平分∠ADP时,求P点坐标;
(3)将抛物线图象绕原点O顺时针旋转90°形成如图2的“心形”图案,其中点M,N分别是旋转前后抛物线的顶点,点E、F是旋转前后抛物线的交点.
①直线EF的解析式是 ;
②点G、H是“心形”图案上两点且关于EF对称,则线段GH的最大值是 .
6. (2023•无锡二模)二次函数y=ax2+bx+4的图象与x轴交于两点A、B,与y轴交于点C,且A(﹣1,0)、B(4,0).
(1)求此二次函数的表达式;
(2)①如图1,抛物线的对称轴m与x轴交于点E,CD⊥m,垂足为D,点F(﹣,0),动点N在线段DE上运动,连接CF、CN、FN,若以点C、D、N为顶点的三角形与△FEN相似,求点N的坐标;
②如图2,点M在抛物线上,且点M的横坐标是1,将射线MA绕点M逆时针旋转45°,交抛物线于点P,求点P的坐标;
(3)已知Q在y轴上,T为二次函数对称轴上一点,且△QOT为等腰三角形,若符合条件的Q恰好有2个,直接写出T的坐标.
7. (2023•沙湾区模拟)如图,抛物线f(x):y=a(x+1)(x﹣5)与x轴交于点A、B(点A位于点B左边),与y轴交于点C(0,.
(1)求抛物线f(x)的解析式;
(2)作点C关于x轴的对称点C',连接线段AC,作∠CAB的平分线AE交抛物线于点E,将抛物线f(x)沿对称轴向下平移经过点C'得到抛物线f'(x).在射线AE上取点F,连接FC,将射线FC绕点F逆时针旋转120°交抛物线f'(x)于点P.当△ACF为等腰三角形时,求点P的横坐标.
8. (2023•灌南县二模)如图,抛物线y=ax2+bx+3经过点A(1,0),B(3,0)两点,与y轴交于点C,其顶点为M,连接MA,MC,AC,过点C作y轴的垂线l.
(1)求该抛物线的表达式;
(2)直线l上是否存在点N,使得S△MBN=2S△MAC?若存在,求出点N的坐标;若不存在,请说明理由.
(3)如图2,若将原抛物线绕点C逆时针旋转45°,求新抛物线与y轴交点P坐标.
9. (2023•红花岗区三模)如图(1),△ABC中,AC=BC=6,∠C=90°,点P在线段AC上,从C点向A点运动,∠PBE=90°,BP=BE,PE交BC于点D,完成下列问题:
(1)①点E到BC边的距离为 ;
②若CD=x,△BDE的面积为S,则S与x的函数关系式为 ;(不写自变量取值范围)
(2)当△BDE的面积为15时,若PC<AC,以C为原点,AC、BC所在直线分别为x、y轴建立坐标系如图(2),抛物线C1过点A、D、B;
①点Q在抛物线C1上,且位于线段PB的下方,过点Q作QN⊥PB,垂足为点N,是否存在点Q,使得QN最长,若存在,请求出QN的长度和Q点坐标;若不存在,请说明理由;
②将抛物线C1绕原点C旋转180°,得到抛物线C2,当﹣2a≤x≤﹣a时(a>0),抛物线C2有最大值2a,求a值.
10. (2023•乳源县三模)如图,对称轴为直线x=﹣1的抛物线y=a(x﹣h)2+k(a≠0)图象与x轴交于点A、B(点A在点B的左侧),与y轴交于点C,其中点B的坐标为(2,0),点C的坐标为(0,4).
(1)求该抛物线的解析式;
(2)如图1,若点P为抛物线上第二象限内的一个动点,点M为线段CO上一动点,当△APC的面积最大时,求△APM周长的最小值;
(3)如图2,将原抛物线绕点A旋转180°,得新抛物线y',在新抛物线y'的对称轴上是否存在点Q使得△ACQ为等腰三角形?若存在,请直接写出点Q的坐标;若不存在,说明理由.
11. (2023秋•亭湖区期末)如图,在平面直角坐标系中,抛物线y=x2+bx+c经过点A(0,﹣3),与x轴的交点为B、C,直线l:y=2x+2与抛物线相交于点C,与y轴相交于点D,P是直线l下方抛物线上一动点.
(1)求抛物线的函数表达式;
(2)过点P作线段PM∥x轴,与直线l相交于点M,当PM最大时,求点P的坐标及PM的最大值;
(3)把抛物线绕点O旋转180°,再向上平移使得新抛物线过(2)中的P点,E是新抛物线与y轴的交点,F为原抛物线对称轴上一点,G为平面直角坐标系中一点,直接写出所有使得以B、E、F、G为顶点、BF为边的四边形是菱形的点G的坐标,并把求其中一个点G的坐标的过程写出来.
12. (2023秋•北京期中)定义:如果抛物线C1的顶点在抛物线C2上,同时,抛物线C2的顶点在抛物线C1上,则称抛物线C1与C2关联.例如,如图,抛物线y=x2的顶点(0,0)在抛物线y=﹣x2+2x上,抛物线y=﹣x2+2x的顶点(1,1)也在抛物线y=x2上,所以抛物线y=x2与y=﹣x2+2x关联.
(1)已知抛物线C1:y=(x+1)2﹣2,分别判断抛物线C2:y=﹣x2+2x+1和抛物线C3:y=2x2+2x+1与抛物线C1是否关联;
(2)抛物线M1:的顶点为A,动点P的坐标为(t,2),将抛物线M1绕点P(t,2)旋转180°得到抛物线M2,若抛物线M1与M2关联,求抛物线M2的解析式;
(3)抛物线M1:的顶点为A,点B是与M1关联的抛物线的顶点,将线段AB绕点A按顺时针方向旋转90°得到线段AB1,若点B1恰好在y轴上,请直接写出点B1的纵坐标.
13. (2023•锡山区一模)如图,抛物线y=x2+bx+c的顶点为M,对称轴是直线x=1,与x轴的交点为A(﹣3,0)和B,将抛物线y=x2+bx+c绕点B逆时针方向旋转90°,点M1、A1为点M、A旋转后的对应点,旋转后的抛物线与y轴相交于C,D两点.
(1)写出点B的坐标及求原抛物线的解析式;
(2)求证A,M,A1三点在同一直线上;
(3)设点P是旋转后抛物线上DM1之间的一动点,是否存在一点P,使四边形PM1MD的面积最大?如果存在,请求出点P的坐标及四边形PM1MD的面积;如果不存在,请说明理由.
14. (2023秋•道里区校级期中)如图,在平面直角坐标系中,点O为坐标原点,直线y=x+3交x轴于点A,y轴于点D,抛物线y=x2+bx﹣3与x轴交于A,B两点,交y轴于点C.
(1)求抛物线的解析式;
(2)P在第三象限抛物线上,P点横坐标为t,连接AP、DP,△APD的面积为s,求s关于t的函数关系式;(不要求写自变量t的取值范围)
(3)在(2)的条件下,PD绕点P逆时针旋转,与线段AD相交于点E,且∠EPD=2∠PDC,过点E作EF⊥PD交PD于G,y轴于点F,连接PF,若,求线段PF的长.
15. (2023秋•大兴区期中)在平面直角坐标系xOy中,已知四边形OABC是平行四边形,点A(4,0),∠AOC=60°,点C的纵坐标为,点D是边BC上一点,连接OD,将线段OD绕点O逆时针旋转60°得到线段OE.
给出如下定义:
如果抛物线y=ax2+bx(a≠0)同时经过点A,E,则称抛物线y=ax2+bx(a≠0)为关于点A,E的“伴随抛物线”.
(1)如图1,当点D与点C重合时,点E的坐标为 ,此时关于点A,E的“伴随抛物线”的解析式为 ;
(2)如图2,当点D在边BC上运动时,连接CE.
①当CE取最小值时,求关于点A,E的“伴随抛物线”的解析式;
②若关于点A,E的“伴随抛物线”y=ax2+bx(a≠0)存在,直接写出a的取值范围.
16. (2023秋•天心区期末)如图1,在平面直角坐标系xOy中,抛物线C:y=﹣x2+bx+c与x轴相交于A,B两点,顶点为D,其中A(﹣4,0),B(4,0),设点F(m,0)是x轴的正半轴上一点,将抛物线C绕点F旋转180°,得到新的抛物线C'.
(1)求抛物线C的函数解析式;
(2)若抛物线C'与抛物线C在y轴的右侧有两个不同的公共点,求m的取值范围;
(3)如图2,P是第一象限内抛物线C上一点,它到两坐标轴的距离相等,点P在抛物线C'上的对应点P',设M是C上的动点,N是C'上的动点,试探究四边形PMP'N能否成为正方形?若能,求出m的值;若不能,请说明理由.
17. (2023•大庆模拟)如图1,在平面直角坐标系xOy中,直线l:与x轴、y轴分别交于点A和点B(0,﹣1),抛物线经过点B,且与直线l的另一个交点为C(4,n).
(1)求n的值和抛物线的解析式;
(2)点D在抛物线上,且点D的横坐标为t(0<t<4).DE∥y轴交直线l于点E,点F在直线l上,且四边形DFEG为矩形(如图2).若矩形DFEG的周长为p,求p与t的函数关系式以及p的最大值;
(3)M是平面内一点,将△AOB绕点M沿逆时针方向旋转90°后,得到△A1O1B1,点A、O、B的对应点分别是点A1、O1、B1.若△A1O1B1的两个顶点恰好落在抛物线上,请直接写出点A1的横坐标.
18. (2023•苏州一模)如图,二次函数y=x2+bx+4的图象与x轴交于点A、B,与y轴交于点C,点A的坐标为(﹣8,0),P是抛物线上一点(点P与点A、B、C不重合).
(1)b= ,点B的坐标是 ;
(2)连接AC、BC,证明:∠CBA=2∠CAB;
(3)点D为AC的中点,点E是抛物线在第二象限图象上一动点,作DE,把点A沿直线DE翻折,点A的对称点为点G,点E运动时,当点G恰好落在直线BC上时,求E点的坐标.
19. (2023•大连模拟)已知抛物线G:y=(m+1)x2+2(n﹣1)x+n+1(m≠﹣1,m为常数)的对称轴与直线y=kx+k(k>0,k为常数)相交于x轴上一点P.
(1)求m与n的数量关系;
(2)若直线y=kx+k与y轴交于点Q,且OQ=OP,
①把直线y=kx+k绕点Q顺时针旋转45°得到的直线与抛物线G相交于A、B两点,若AB=4,求m的值;
②将直线y=kx+k向上平移2k个单位,得到的直线与抛物线G的两个交点的横坐标x1,x2满足﹣2<x1<x2<2,求m的取值范围.
20. (2023•兰州)如图1,二次函数y=a(x+3)(x﹣4)图象交坐标轴于点A,B(0,﹣2),点P为x轴上一动点.
(1)求二次函数y=a(x+3)(x﹣4)的表达式;
(2)过点P作PQ⊥x轴分别交线段AB,抛物线于点Q,C,连接AC.当OP=1时,求△ACQ的面积;
(3)如图2,将线段PB绕点P逆时针旋转90°得到线段PD.当点D在抛物线上时,求点D的坐标.
专题18二次函数与旋转变换综合问题
【例1】 (2023•凉山州)在平面直角坐标系xOy中,已知抛物线y=﹣x2+bx+c经过点A(﹣1,0)和点B(0,3),顶点为C,点D在其对称轴上,且位于点C下方,将线段DC绕点D按顺时针方向旋转90°,点C落在抛物线上的点P处.
(1)求抛物线的解析式;
(2)求点P的坐标;
(3)将抛物线平移,使其顶点落在原点O,这时点P落在点E的位置,在y轴上是否存在点M,使得MP+ME的值最小,若存在,求出点M的坐标;若不存在,请说明理由.
【分析】(1)利用待定系数法求抛物线解析式;
(2)利用配方法得到y=﹣(x﹣1)2+4,则根据二次函数的性质得到C点坐标和抛物线的对称轴为直线x=1,如图,设CD=t,则D(1,4﹣t),根据旋转性质得∠PDC=90°,DP=DC=t,则P(1+t,4﹣t),然后把P(1+t,4﹣t)代入y=﹣x2+2x+4得到关于t的方程,从而解方程求出t,即可得到点P的坐标;
(3)P点坐标为(2,3),顶点C坐标为(1,4),利用抛物线的平移规律确定E点坐标为(1,﹣1),找出点E关于y轴的对称点F(﹣1,﹣1),连接PF交y轴于M,则MP+ME=MP+MF=PF的值最小,然后利用待定系数法求出直线PF的解析式,即可得到点M的坐标.
【解析】(1)把A(﹣1,0)和点B(0,3)代入y=﹣x2+bx+c,
得,
解得:,
∴抛物线解析式为y=﹣x2+2x+3;
(2)∵y=﹣(x﹣1)2+4,
∴C(1,4),抛物线的对称轴为直线x=1,
如图,设CD=t,则D(1,4﹣t),
∵线段DC绕点D按顺时针方向旋转90°,点C落在抛物线上的点P处,
∴∠PDC=90°,DP=DC=t,
∴P(1+t,4﹣t),
把P(1+t,4﹣t)代入y=﹣x2+2x+3得:
﹣(1+t)2+2(1+t)+3=4﹣t,
整理得t2﹣t=0,
解得:t1=0(舍去),t2=1,
∴P(2,3);
(3)∵P点坐标为(2,3),顶点C坐标为(1,4),将抛物线平移,使其顶点落在原点O,这时点P落在点E的位置,
∴E点坐标为(1,﹣1),
∴点E关于y轴的对称点F(﹣1,﹣1),
连接PF交y轴于M,则MP+ME=MP+MF=PF的值最小,
设直线PF的解析式为y=kx+n,
∴,
解得:,
∴直线PF的解析式为y=x+,
∴点M的坐标为(0,).
【例2】. (2023•梧州)如图,在平面直角坐标系中,直线y=﹣x﹣4分别与x,y轴交于点A,B,抛物线y=x2+bx+c恰好经过这两点.
(1)求此抛物线的解析式;
(2)若点C的坐标是(0,6),将△ACO绕着点C逆时针旋转90°得到△ECF,点A的对应点是点E.
①写出点E的坐标,并判断点E是否在此抛物线上;
②若点P是y轴上的任一点,求BP+EP取最小值时,点P的坐标.
【分析】(1)根据直线解析式可得点A、B的坐标,代入二次函数解析式,解方程即可;
(2)①由旋转的性质可得E(6,3),当x=6时,y==3,可知点E在抛物线上;
②过点E作EH⊥AB,交y轴于P,垂足为H,sin∠ABO=,则HP=BP,得BP+EP=HP+PE,可知HP+PE的最小值为EH的长,从而解决问题.
【解析】(1)∵直线y=﹣x﹣4分别与x,y轴交于点A,B,
∴当x=0时,y=﹣4;当y=0时,x=﹣3,
∴A(﹣3,0),B(0,﹣4),
∵抛物线y=x2+bx+c恰好经过这两点.
∴,
解得,
∴y=﹣x﹣4;
(2)①∵将△ACO绕着点C逆时针旋转90°得到△ECF,
∴∠OCF=90°,CF=CO=6,EF=AO=3,EF∥y轴,
∴E(6,3),
当x=6时,y==3,
∴点E在抛物线上;
②过点E作EH⊥AB,交y轴于P,垂足为H,
∵A(﹣3,0),B(0,﹣4),
∴OA=3,OB=4,
∴AB=5,
∵sin∠ABO=,
∴HP=BP,
∴BP+EP=HP+PE,
∴当E,P,H三点共线时,HP+PE有最小值,最小值为EH的长,
作EG⊥y轴于G,
∵∠GEP=∠ABO,
∴tan∠GEP=tan∠ABO,
∴,
∴,
∴PG=,
∴OP=﹣3=,
∴P(0,﹣).
【例3】. (2023•辽宁)如图,抛物线y=ax2﹣3x+c与x轴交于A(﹣4,0),B两点,与y轴交于点C(0,4),点D为x轴上方抛物线上的动点,射线OD交直线AC于点E,将射线OD绕点O逆时针旋转45°得到射线OP,OP交直线AC于点F,连接DF.
(1)求抛物线的解析式;
(2)当点D在第二象限且=时,求点D的坐标;
(3)当△ODF为直角三角形时,请直接写出点D的坐标.
【分析】(1)将点A(﹣4,0),C(0,4)代入y=ax2﹣3x+c,即可求解;
(2)过点D作DG⊥AB交于G,交AC于点H,设D(n,﹣n2﹣3n+4),H(n,n+4),由DH∥OC,可得==,求出D(﹣1,6)或(﹣3,4);
(3)设F(t,t+4),当∠FDO=90°时,过点D作MN⊥y轴交于点N,过点F作FM⊥MN交于点M,证明△MDF≌△NOD(AAS),可得D点纵坐标为2,求出D点坐标为(,2)或(,2);当∠DFO=90°时,过点F作KL⊥x轴交于L点,过点D作DK⊥KL交于点K,证明△KDF≌△LFO(AAS),得到D点纵坐标为4,求得D(0,4)或(﹣3,4).
【解析】(1)将点A(﹣4,0),C(0,4)代入y=ax2﹣3x+c,
∴,
解得,
∴y=﹣x2﹣3x+4;
(2)过点D作DG⊥AB交于G,交AC于点H,
设直线AC的解析式为y=kx+b,
∴,
解得,
∴y=x+4,
设D(n,﹣n2﹣3n+4),H(n,n+4),
∴DH=﹣n2﹣4n,
∵DH∥OC,
∴==,
∵OC=4,
∴DH=3,
∴﹣n2﹣4n=3,
解得n=﹣1或n=﹣3,
∴D(﹣1,6)或(﹣3,4);
(3)设F(t,t+4),
当∠FDO=90°时,过点D作MN⊥y轴交于点N,过点F作FM⊥MN交于点M,
∵∠DOF=45°,
∴DF=DO,
∵∠MDF+∠NDO=90°,∠MDF+∠MFD=90°,
∴∠NDO=∠MFD,
∴△MDF≌△NOD(AAS),
∴DM=ON,MF=DN,
∴DN+ON=﹣t,DN=ON+(﹣t﹣4),
∴DN=﹣t﹣2,ON=2,
∴D点纵坐标为2,
∴﹣x2﹣3x+4=2,
解得x=或x=,
∴D点坐标为(,2)或(,2);
当∠DFO=90°时,过点F作KL⊥x轴交于L点,过点D作DK⊥KL交于点K,
∵∠KFD+∠LFO=90°,∠KFD+∠KDF=90°,
∴∠LFO=∠KDF,
∵DF=FO,
∴△KDF≌△LFO(AAS),
∴KD=FL,KF=LO,
∴KL=t+4﹣t=4,
∴D点纵坐标为4,
∴﹣x2﹣3x+4=4,
解得x=0或x=﹣3,
∴D(0,4)或(﹣3,4);
综上所述:D点坐标为(,2)或(,2)或(0,4)或(﹣3,4).
【例4】 (2023•河池)在平面直角坐标系中,抛物线L1:y=ax2+2x+b与x轴交于两点A,B(3,0),与y轴交于点C(0,3).
(1)求抛物线L1的函数解析式,并直接写出顶点D的坐标;
(2)如图,连接BD,若点E在线段BD上运动(不与B,D重合),过点E作EF⊥x轴于点F,设EF=m,问:当m为何值时,△BFE与△DEC的面积之和最小;
(3)若将抛物线L1绕点B旋转180°得抛物线L2,其中C,D两点的对称点分别记作M,N.问:在抛物线L2的对称轴上是否存在点P,使得以B,M,P为顶点的三角形为等腰三角形?若存在,直接写出所有符合条件的点P的坐标;若不存在,请说明理由.
【分析】(1)利用待定系数法求出a,b的值即可;
(2)如图1中,连接BC,过点C作CH⊥BD于点H.设抛物线的对称轴交x轴于点T.首先证明∠DCB=90°,利用面积法求出CH,构建二次函数,利用二次函数的性质即可解决问题;
(3)如图2中,由题意抛物线L2的对称轴x=5,M(6,﹣3).设P(5,m),分三种情形:当BP=BM=3时,当PB=PM时,当BM=PM时,分别构建方程求解即可.
【解析】(1)∵y=ax2+2x+b经过B(3,0),C(0,3),
∴,
∴,
∴抛物线的解析式为y=﹣x2+2x+3,
∵y=﹣(x﹣1)2+4,
∴抛物线的顶点D(1,4);
(2)如图1中,连接BC,过点C作CH⊥BD于点H.设抛物线的对称轴交x轴于点T.
∵C(0,3),B(3,0),D(1,4),
∴BC=3,CD=,BD==2,
∴BC2+CD2=BD2,
∴∠BCD=90°,
∵•CD•CB=•BD•CH,
∴CH==,
∵EF⊥x轴,DT⊥x轴,
∴EF∥DT,
∴==,
∴==,
∴BE=m,BF=m,
∴△BFE与△DEC的面积之和S=×(2﹣m)×+×m×m=(m﹣)2+,
∵>0,
∴S有最小值,最小值为,此时m=,
∴m=时,△BFE与△DEC的面积之和有最小值.
解法二:求两个三角形面积和的最小值,即就是求四边形OCEF面积的最大值.求出四边形OCEF的面积的最大值即可.
(3)存在.
理由:如图2中,由题意抛物线L2的对称轴x=5,M(6,﹣3).
设P(5,m),
当BP=BM=3时,22+m2=(3)2,
∴m=±,
∴P1(5,),P2(5,﹣),
当PB=PM时,22+m2=12+(m+3)2,
解得,m=﹣1,
∴P3(5,﹣1),
当BM=PM时,(3)2=12+(m+3)2,
解得,m=﹣3±,
∴P4(5,﹣3+),P5(5,﹣3﹣),
综上所述,满足条件的点P的坐标为P1(5,),P2(5,﹣),P3(5,﹣1),P4(5,﹣3+),P5(5,﹣3﹣).
一.解答题(共20小题)
1. (2023•碑林区校级三模)如图,在平面直角坐标系中,抛物线W1与x轴交于A,B两点,与y轴交于点C(0,﹣6),顶点为D(﹣2,2).
(1)求抛物线W1的表达式;
(2)将抛物线W1绕原点O旋转180°得到抛物线W2,抛物线W2的顶点为D′,在抛物线W2上是否存在点M,使S△D′AD=S△D′DM?若存在,请求出点M的坐标;若不存在,请说明理由.
【分析】(1)利用待定系数法解得即可;
(2)由题意求得抛物线W2的顶点坐标和解析式,在坐标系中画出抛物线W2的图象,利用S△DAD′=S△ADO+S△AOD′求出三角形DD′A的面积;过点D′作x轴的平行线EF,过点D作DE⊥EF于点E,交x轴于点G,过点M作MF⊥EF于点F,交x轴于点H,利用D,D′的坐标表示出线段DG,OG,DE,D′E的长度,设点M(m,2m2﹣8m+6),则MH=2m2﹣8m+6,OH=m,MF=MH+HF=2m2﹣8m+6+2=2m2﹣8m+8,D′F=m﹣2,EF=OG+OH=m+2,利用S△DD′M=S梯形DEFM﹣S△DED′﹣S△MD′F,用m的代数式表示出S△DD′M,利用已知条件列出m的方程,解方程即可求得结论.
【解析】(1)设抛物线W1的解析式为:y=ax2+bx+c,
抛物线W1经过点C(0,﹣6),顶点坐标D(﹣2,2),
∴,
解得:.
∴抛物线W1的表达式为:y=﹣2x2﹣8x﹣6;
(2)在抛物线W2上存在点M,使S△DAD′=S△DD′M.理由:
∵将抛物线W1绕原点O旋转180°得到抛物线W2,抛物线W2的顶点为D′,
∴D′(2,﹣2).
∴抛物线W2的解析式为y=2(x﹣2)2﹣2=2x2﹣8x+6.
如图,在坐标系中画出抛物线W2的图象,
由题意得:DD′经过点O,则S△DAD′=S△ADO+S△AOD′.
过点D′作x轴的平行线EF,过点D作DE⊥EF于点E,交x轴于点G,过点M作MF⊥EF于点F,交x轴于点H,
∵D(﹣2,2),D′(2,﹣2),
∴DG=OG=2,DE=4,D′E=4,FH=2.
令y=0,则﹣2x2﹣8x﹣6=0.
解得:x=﹣1或﹣3.
∴A(﹣3,0),B(﹣1,0).
∴OA=3.
∴S△DAD′=S△ADO+S△AOD′=×3×2+×3×2=6.
设点M(m,2m2﹣8m+6),
则MH=2m2﹣8m+6,OH=m.
∴MF=MH+HF=2m2﹣8m+6+2=2m2﹣8m+8,
D′F=m﹣2,
EF=OG+OH=m+2.
∵S△DD′M=S梯形DEFM﹣S△DD′E﹣S△MD′F,
∴S△DD′M=(DE+MF)•EF﹣DE•D′E﹣MF•D′F
=(4+2m2﹣8m+8)(m+2)﹣×4×4﹣(2m2﹣8m+8)(m﹣2)
=4m2﹣14m+12.
∵S△DD′M=S△DD′A,
∴4m2﹣14m+12=6.
解得:m=3或.
当m=3时,2m2﹣8m+6=0,
当m=时,2m2﹣8m+6=,
∴M(3,0)或(,).
∴在抛物线W2上存在点M,使S△D′AD=S△D′DM.点M的坐标为(3,0)或(,).
2. (2023•双流区模拟)如图,抛物线C:y=ax2+6ax+9a﹣8与x轴相交于A,B两点(点A在点B的左侧),已知点B的横坐标是2,抛物线C的顶点为D.
(1)求a的值及顶点D的坐标;
(2)点P是x轴正半轴上一点,将抛物线C绕点P旋转180°后得到抛物线C1,记抛物线C1的顶点为E,抛物线C1与x轴的交点为F,G(点F在点G的右侧).当点P与点B重合时(如图1),求抛物线C1的表达式;
(3)如图2,在(2)的条件下,从A,B,D中任取一点,E,F,G中任取两点,若以取出的三点为顶点能构成直角三角形,我们就称抛物线C1为抛物线C的“勾股伴随同类函数”.当抛物线C1是抛物线C的勾股伴随同类函数时,求点P的坐标.
【分析】(1)将点B(2,0)代入y=ax2+6ax+9a﹣8,即可求出a,把抛物线的解析式化为顶点式即可得出顶点坐标;
(2)如图1,连接DE,作DH⊥x轴于H,作EM⊥x轴于M,由△DBH≌△EBM(AAS),可得EM=DH=8,BM=BH=5,故抛物线C1的顶点E的坐标为(7,8),即可得出抛物线C1的函数表达式为y=﹣(x﹣7)2+8;
(3)设点E(m,8),如图2,作DH⊥x轴于H,EM⊥x轴于M,EN⊥DN于N,根据旋转可得:FG=AB=2BH=10,进而可得:点H的坐标为(﹣3,0),点N的坐标为(m,﹣8),再分类讨论即可得出答案.
【解析】(1)由y=ax2+6ax+9a﹣8得y=a(x+3)2﹣8,
∴顶点D的坐标为(﹣3,﹣8),
∵点B(2,0)在抛物线C上,
∴0=a(2+3)2﹣8,
解得:a=;
(2)如图1,连接DE,作DH⊥x轴于H,作EM⊥x轴于M,
根据题意,点D,E关于点B(2,0)成中心对称,
∴DE过点B,且DB=EB,
在△DBH和△EBM中,
,
∴△DBH≌△EBM(AAS),
∴EM=DH=8,BM=BH=5,
∴抛物线C1的顶点E的坐标为(7,8),
∵抛物线C1由C绕点P旋转180°后得到,
∴抛物线C1的函数表达式为y=﹣(x﹣7)2+8;
(3)∵抛物线C1由C绕x轴上的点P旋转180°后得到,
∴顶点D,E关于点P成中心对称,由(2)知:点E的纵坐标为8,
设点E(m,8),
如图2,作DH⊥x轴于H,EM⊥x轴于M,EN⊥DN于N,
∵旋转中心P在x轴上,
∴FG=AB=2BH=10,
∴点H的坐标为(﹣3,0),点N的坐标为(m,﹣8),
根据勾股定理得,EF2=82+52=89,
显然,△AEG和△BEG不可能是直角三角形,
①当△AEF是直角三角形时,显然只能有∠AEF=90°,
根据勾股定理得:
AE2=AM2+EM2=(m+8)2+82=m2+16m+128,
AE2=AF2﹣EF2=(m+13)2﹣89=m2+26m+80,
∴m2+16m+128=m2+26m+80,
解得:m=,
∴OP=(m+3)﹣3=(m﹣3)=×(﹣3)=,
∴点P的坐标为(,0);
②当△BEF是直角三角形时,显然只能有∠BEF=90°,
根据勾股定理得:
BE2=BM2+EM2=(m﹣2)2+82=m2﹣4m+68,
BE2=BF2﹣EF2=(m+3)2﹣89=m2+6m﹣80,
∴m2﹣4m+68=m2+6m﹣80,
解得:m=,
∴OP=(m﹣3)=×(﹣3)=,
∴点P的坐标为(,0),
③当△DEF是直角三角形时,
DE2=EN2+DN2=162+(m+3)2=m2+6m+265,
DF2=DH2+HF2=82+(m+8)2=m2+16m+128,
i)当∠DEF=90°时,DE2+EF2=DF2,
即m2+6m+265+89=m2+16m+128,
解得:m=,
∴OP=(m﹣3)=×(﹣3)=,
∴点P的坐标为(,0);
ii)当∠DFE=90°时,DF2+EF2=DE2,
即m2+16m+128+89=m2+6m+265,
解得:m=,
∴OP=(m﹣3)=×(﹣3)=,
∴点P的坐标为(,0);
iii)∵DE>EN=16>EF,
∴∠EDF≠90°,
综上所述,当抛物线C1是抛物线C的勾股伴随同类函数时,点P的坐标为(,0)或(,0)或(,0).
3. (2023•灞桥区校级模拟)已知:如图,在平面直角坐标系xOy中,直线y=x+6与x轴、y轴的交点分别为A、B,其中点C是x轴上一点,OC=3.
(1)求过A、B、C三点的抛物线L的解析式;
(2)将抛物线L绕着点O旋转180°得到抛物线L1,抛物线L1与x轴交于F点、E点(点F在点E的左侧),与y轴交于点M,则抛物线L1的对称轴上是否存在一点Q,使|QF﹣QM|的值最大?若存在,求出点Q的坐标及其最大值,若不存在,请说明理由.
【分析】(1)由一次函数解析式可得A,B坐标,由OC=3可得点C坐标,然后通过待定系数法求函数解析式.
(2)先求出抛物线L1解析式,根据抛物线的对称性可得抛物线与x轴,y轴的交点坐标,点Q为抛物线对称轴与直线EM交点时,|QF﹣QM|=EM的值最大.
【解析】(1)将x=0代入y=x+6得y=6,
∴点B坐标为(0,6),
将y=0代入y=x+6得0=x+6,
解得x=8,
∴点A坐标为(8,0),
∵OC=3,
∴点C坐标为(3,0),
设抛物线解析式为y=a(x﹣8)(x﹣3),
将(0,6)代入y=a(x﹣8)(x﹣3)得6=24a,
解得a=,
∴y=(x﹣8)(x﹣3)=x2﹣x+6.
(2)将抛物线L绕着点O旋转180°得到抛物线L1解析式为y=﹣(x+8)(x+3)=﹣x2﹣x﹣6,
∵抛物线L经过(3,0),(8,0),
∴抛物线L1经过E(﹣3,0),F(﹣8,0),与y轴交于点M(0,﹣6),
设直线FM解析式为y=kx+b,
将E(﹣3,0),M(0,﹣6)代入y=kx+b得,
解得,
∴y=﹣2x﹣6,
∵抛物线经E(﹣3,0),F(﹣8,0),
∴抛物线对称轴为直线x==﹣,
∵抛物线对称轴为线段EF的垂直平分线,
∴QF=QE,
∴点Q为抛物线对称轴与直线EM交点时,|QF﹣QM|=EM的值最大,
将x=﹣代入y=﹣2x﹣6得y=﹣2×(﹣)﹣6=5,
∴点Q坐标为(﹣,5)时,|QF﹣QM|的最大值为EM==3.
4. (2023•莲湖区二模)已知抛物线W1:y=ax2﹣bx﹣3与x轴交于A(﹣1,0)、B(3,0)两点与y轴交于点C,顶点为D.
(1)求抛物线W1的表达式;
(2)将抛物线W1绕原点O旋转180°后得到抛物线W2,W2的顶点为D',点M为W2上的一点,当△D'DM的面积等于△ABC的面积时,求点M的坐标.
【分析】(1)利用待定系数法解得即可;
(2)由题意求得抛物线W2的顶点坐标和解析式,在坐标系中画出抛物线W2的图象,利用待定系数法求得直线DD′的解析式,过点M作MN∥x轴,交DD′于N,利用S△DD′M=S△MND′+S△MND,用m的代数式表示出S△DD′M,利用已知条件列出m的方程,解方程即可求得结论.
【解析】(1)∵抛物线W1:y=ax2﹣bx﹣3与x轴交于A(﹣1,0)、B(3,0)两点,
∴,
解得:.
∴抛物线W1的表达式为:y=x2﹣2x﹣3;
(2)∵y=x2﹣2x﹣3=(x﹣1)2﹣4,
∴D(1,﹣4),
∵将抛物线W1绕原点O旋转180°后得到抛物线W2,W2的顶点为D',
∴D′(﹣1,4),
∴抛物线W2的解析式为y=﹣(x+1)2+4=﹣x2﹣2x+3.
如图,在坐标系中画出抛物线W2的图象,
当x=0时,y=x2﹣2x﹣3=﹣3,
∴C(0,﹣3),
∵A(﹣1,0)、B(3,0),
∴AB=4,
∴S△ABC==6,
过点M作MN∥x轴,交DD′于N,
∵D(1,﹣4),D′(﹣1,4),
∴直线DD′为y=﹣4x,
设点M(m,﹣m2﹣2m+3),则N(,﹣m2﹣2m+3),
∴MN=﹣m=,
∴S△DD′M=××(4+4)=m2﹣2m﹣3,
∵△D'DM的面积等于△ABC的面积,
∴m2﹣2m﹣3=6.
解得:m=1±.
当m=1+时,﹣m2﹣2m+3=﹣4﹣10,
当m=1﹣时,﹣m2﹣2m+3=4﹣10,
∴M(1+,﹣4﹣10)或(1﹣,4﹣10).
5. (2023•深圳三模)已知抛物线y=ax2+c过点A(﹣2,0)和D(﹣1,3)两点,交x轴于另一点B.
(1)求抛物线解析式;
(2)如图1,点P是BD上方抛物线上一点,连接AD,BD,PD,当BD平分∠ADP时,求P点坐标;
(3)将抛物线图象绕原点O顺时针旋转90°形成如图2的“心形”图案,其中点M,N分别是旋转前后抛物线的顶点,点E、F是旋转前后抛物线的交点.
①直线EF的解析式是 y=x ;
②点G、H是“心形”图案上两点且关于EF对称,则线段GH的最大值是 .
【分析】(1)用待定系数法求函数解析式即可;
(2)过过点B作BE⊥x轴交DP延长线于点E,过D作DF⊥x于点F,证明△DAB≌△DEB,求得点E坐标,进而求得直线DE的解析式,联立抛物线解析式即可求解;
(3)①根据顺时针旋转90°后的坐标特征可知对称轴为y=x;②连接GH,交EF与点K,则GH=2GK,过点G作x轴的垂线,交EF于点I,当GK最大时,△GFE面积最大,设G(m,﹣m2+4),则I(m,m),根据S△GFE=GN•(xE﹣xF)以及二次函数的性质求得当m=﹣时,△GFE面积最大,求出此时点G坐标,再根据①求出点H坐标,再利用中点坐标公式求出求得K的坐标,从而求出GH即可.
【解析】(1)∵抛物线y=ax2+c过点A(﹣2,0)和D(﹣1,3)两点,
∴,
解得,
∴抛物线解析式为y=﹣x2+4;
(2)过点B作BE⊥x轴交DP延长线于点E,过D作DF⊥x于点F,
由y=﹣x2+4,令y=0,则﹣x2+4=0,
解得:x1=﹣2,x2=2,
则B(2,0),
∵DF=3,BF=2﹣(﹣1)=3,
∴DF=BF,
∴∠DBF=45°,
∴∠DBE=45°,
又∵DB=DB,BD平分∠ADP,
∴△DSA≌△DEB(ASA),
∴BA=BE,
∵B(2,0),
∴E(2,4),
设直线DE的解析式为y=kx+b,
则,
解得,
∴直线DE的解析式为y=x+,
联立,
解得或,
则P(,);
(3)①∵抛物线关于y轴对称,所以旋转后图形关于x轴对称,
∴对于抛物线上任意一点P(a,b) 关于原点旋转90°后对应点为P1(b,﹣a) 在旋转后图形上,
P1(b,﹣a) 关于x轴对称的点P2(b,a) 在旋转后图形上,
∵P(a,b)与P2(b,a)关于y=x对称,
∴图形2关于y=x对称,
∴直线EF的解析式为y=x,
故答案为:y=x;
②如图,连接GH,交EF与点K,则GH=2GK,
过点G作x轴的垂线,交EF于点I,
∴当GK最大时,△GFE面积最大,
又∵S△GFE=GI•(xE﹣xF),
设G(m,﹣m2+4),则I(m,m),
∴GI=yG﹣yI=﹣m2+4﹣m=﹣(m+)2+,
∴当m=﹣时,△GFE面积最大,
∴G(﹣,),
由①可知G(﹣,)关于y=x的对称点H(,﹣),
∴K(,),
∴GK==,
∴GH=2GK=,
∴GH的最大值为,
故答案为:.
6. (2023•无锡二模)二次函数y=ax2+bx+4的图象与x轴交于两点A、B,与y轴交于点C,且A(﹣1,0)、B(4,0).
(1)求此二次函数的表达式;
(2)①如图1,抛物线的对称轴m与x轴交于点E,CD⊥m,垂足为D,点F(﹣,0),动点N在线段DE上运动,连接CF、CN、FN,若以点C、D、N为顶点的三角形与△FEN相似,求点N的坐标;
②如图2,点M在抛物线上,且点M的横坐标是1,将射线MA绕点M逆时针旋转45°,交抛物线于点P,求点P的坐标;
(3)已知Q在y轴上,T为二次函数对称轴上一点,且△QOT为等腰三角形,若符合条件的Q恰好有2个,直接写出T的坐标.
【分析】(1)先求得点C的坐标,设抛物线的解析式为y=a(x+1)(x﹣4),将点C的坐标代入求得a的值,从而得到抛物线的解析式;
(2)①当点C、D、N为顶点的三角形与△FEN相似时分两种情况:△CDN∽△FEN和△CDN∽△NEF,列比例式可解答;
②如图2所示:过点A作GH∥y轴,过点M作MG⊥GH于G,过点A作AE⊥AM,交MP于点E,证明△AEM是等腰直角三角形,得AM=AE,计算点M的坐标,证明△MGA≌△AHE(AAS),则EH=AG=6,AH=GM=2,利用待定系数法可得直线EA的解析式为y=−2x+8,与二次函数解析式联立方程,解出可得结论;
(3)分T在x轴上,x轴上方和下方三种情况:根据符合条件的Q恰好有2个正确画图可得结论.
【解析】(1)y=ax2+bx+4,
当x=0时,y=4,
∴C(0,4),
设抛物线的解析式为y=a(x+1)(x−4),
将点C的坐标代入得:−4a=4,解得a=−1,
∴抛物线的解析式为y=−x2+3x+4;
(2)①如图1,抛物线的对称轴是:x=−=,
∴CD=,EF=+==,
设点N的坐标为(,a)则ND=4−a,NE=a,
当△CDN∽△FEN时,=,
即=,
解得a=,
∴点N的坐标为(,);
当△CDN∽△NEF时,=,
即=,
解得:a1=a2=2,
∴点N的坐标为(,2),
综上所述,点N的坐标为(,)或(,2);
②如图2所示:过点A作GH∥y轴,过点M作MG⊥GH于G,过点A作AE⊥AM,交MP于点E,
∵∠AMP=45°,∠MAE=90°,
∴△AEM是等腰直角三角形,
∴AM=AE,
将x=1代入抛物线的解析式得:y=6,
∴点M的坐标为(1,6),
∴MG=2,AG=6,
∵∠GAM+∠EAH=90°,∠EAH+∠AEH=90°,
∴∠GAM=∠AEH,
∵∠G=∠H=90°,
∴△MGA≌△AHE(AAS),
∴EH=AG=6,AH=GM=2,
∴E(5,﹣2),
设ME的解析式为y=kx+b,
将点A和点E的坐标代入得:,
解得:,
∴直线EA的解析式为y=−2x+8,
﹣2x+8=﹣x2+3x+4,
解得:x=1(舍)或x=4,
将x=4代入y=−2x+8得:y=0,
∴点P的坐标为(4,0);
(3)分种情况:
①如图3,当T在x轴上时,满足条件,此时T(,0);
②如图4,当T在x轴的上方时,
∵△QOT为等腰三角形,且符合条件的Q恰好有2个,
∴OT=OQ2=OQ1=Q1T,
∴△OQ1T是等边三角形,
∴∠TOQ1=60°,
∴∠BOT=30°,
∵OE=,
∵tan30°==,
∴ET=,
∴T(,);
③当T在x轴的下方时,同理得T(,﹣);
综上,T的坐标为(,0)或(,)或(,﹣).
7. (2023•沙湾区模拟)如图,抛物线f(x):y=a(x+1)(x﹣5)与x轴交于点A、B(点A位于点B左边),与y轴交于点C(0,.
(1)求抛物线f(x)的解析式;
(2)作点C关于x轴的对称点C',连接线段AC,作∠CAB的平分线AE交抛物线于点E,将抛物线f(x)沿对称轴向下平移经过点C'得到抛物线f'(x).在射线AE上取点F,连接FC,将射线FC绕点F逆时针旋转120°交抛物线f'(x)于点P.当△ACF为等腰三角形时,求点P的横坐标.
【分析】(1)直接将点C的坐标代入抛物线f(x):y=a(x+1)(x﹣5)中,解方程即可得结论;
(2)根据对称性可得C'(0,﹣),由平移得抛物线f'(x)的解析式为:y=﹣x2+x﹣,可得∠ACO=30°,∠CAO=60°,分三种情况:①AC=AF,②AC=CF,③AQ=CF,分别计算可得点P的横坐标.
【解析】(1)把点C(0,)代入抛物线f(x):y=a(x+1)(x﹣5)中得:
﹣5a=,解得:a=﹣,
∴y=﹣ (x+1)(x﹣5)=﹣ (x2﹣4x﹣5)=﹣x2+x+,
∴抛物线f(x)的表达式为y=﹣x2+x+;
(2)∵点C关于x轴的对称点C′,
∴C'(0,﹣),
∵原抛物线沿对称轴向下平移经过点C′得到抛物线f'(x),
∴抛物线f'(x)的解析式为:y=﹣x2+x﹣,
∵y=﹣x2+x+与x轴交于点A、B(点A位于点B左边),
令y=0,则﹣x2+x﹣=0,解得x1=﹣1,x2=5,
∴A(﹣1,0),B(5,0),
∵C(0,),
∴OA=1,OC=,
∴AC=2,
∴∠ACO=30°,∠CAO=60°,
∵AE平分∠CAO,
∴∠CAF=30°,
分三种情况:
①当AC=AF=2时,如图,设FP交y轴于G,过点F作FL⊥y轴于L,FH⊥x轴于H,过点G作GK⊥CF,交CF的延长线于K,
∴∠ACF=∠AFC==75°,
∴∠OCF=45°,
Rt△AFH中,FH=AF=1,AH=,
∴F(﹣1,1),
∵CL=FL=﹣1,
∴CF=FL=(﹣1),
Rt△CGK中,∠GFK=180°﹣∠CFP=180°﹣120°=60°,
设FK=m,GK=m,
∵∠OCF=45°,
∴△GCK是等腰直角三角形,
∴CK=GK,
∴(﹣1)+m=m,
∴m=,
∴CG=KG=m=2,
∴G(0,﹣)
可得直线PF的解析式为:y=(2+)x﹣,
则,解得:,,
∴P(0,﹣)或(,﹣12﹣);
②当AC=CF时,如图,∠CAF=∠CFA=30°,
∴∠ACQ=120°,
∴∠OCF=90°,
∴F(2,),
∵y=﹣x2+x+=﹣(x﹣2)2+,
∴抛物线f(x)的对称轴是:x=2,
∴F在DF上,
延长PF交y轴于G,
∵∠CFP=120°,
∴∠GFC=60°,
Rt△GCF中,∠CGF=30°,
∵CF=2,
∴CG=2,
∴OG=3,
∴G(0,3),
∴GF的解析式为:y=﹣x+3,
∴,解得,,
∴P(4,﹣)或(5,﹣2);
③当CF=AF时,如图,∠CFA=120°,此种情况不符合题意;
综上,当△CAQ为等腰三角形时,点P的横坐标是0或4或5或.
8. (2023•灌南县二模)如图,抛物线y=ax2+bx+3经过点A(1,0),B(3,0)两点,与y轴交于点C,其顶点为M,连接MA,MC,AC,过点C作y轴的垂线l.
(1)求该抛物线的表达式;
(2)直线l上是否存在点N,使得S△MBN=2S△MAC?若存在,求出点N的坐标;若不存在,请说明理由.
(3)如图2,若将原抛物线绕点C逆时针旋转45°,求新抛物线与y轴交点P坐标.
【分析】(1)直接代入A(1,0),B(3,0)两点坐标即可求解;
(2)如图所示,先求出△MAC的面积为1,然后设出直线MN与x轴的交点坐标E,表示出S△MBN=|xE﹣xB|×(yN﹣yM)=|xE﹣3|×4=2|xE﹣3|,最后根据S△MBN=2S△MAC,求出点N的坐标;
(3)将CP绕点C顺时针旋转45°交原抛物线于点P′,即可得出直线CP′的表达式,从而求出P′的坐标,进而算出CP′的长度,最后得出点P的坐标.
【解析】(1)将A(1,0),B(3,0)代入抛物线y=ax2+bx+3中,
则,
解得:,
∴抛物线的表达式为y=x2﹣4x+3;
(2)假设存在这样的点N,设直线MC与x轴交于点D,直线MN与x轴交于点E,如图:
∵y=x2﹣4x+3=(x﹣2)2﹣1,
∴M(2,﹣1)
令x=0,则y=3,
∴C(0,3),
设直线MC的解析式为y=kx+m,
则,
解得:,
∴直线MC的解析式为y=﹣2x+3,
令y=0,则﹣2x+3=0,
解得x=,
∴点D坐标为(,0),
∴S△MAC=(xD﹣xA)(yC﹣yM)=××4=1,
S△MBN=|xE﹣xB|×(yN﹣yM)=|xE﹣3|×4=2|xE﹣3|,
∵S△MBN=2S△MAC,
∴2|xE﹣3|=2,
解得:xE=4或xE=2,
∴点E的坐标为(4,0)或(2,0),①当M为(2,﹣1),E为(2,0)时,直线MN的表达式为:x=2,
∴点N的坐标为(2,3),
②当M为(2,﹣1),E为(4,0)时,
设直线MN的表达式为y=nx+g,
则,
解得:,
∴直线MN的表达式为y=x﹣2,
联立,得,
∴点N的坐标为(10,3),
∴点N的坐标为(2,3)或(10,3);
(3)如图所示,将CP绕点C顺时针旋转45°交原抛物线于点P′,
∵CP′与x轴的夹角为45°,
∴CP′与直线y=x平行,
则lCP′:y=x+3,
联立,
解得,
∴P′(5,8),
∴CP′==5,
∴CP=5,
∴点P坐标为(0,3+5).
9. (2023•红花岗区三模)如图(1),△ABC中,AC=BC=6,∠C=90°,点P在线段AC上,从C点向A点运动,∠PBE=90°,BP=BE,PE交BC于点D,完成下列问题:
(1)①点E到BC边的距离为 6 ;
②若CD=x,△BDE的面积为S,则S与x的函数关系式为 S=18﹣3x ;(不写自变量取值范围)
(2)当△BDE的面积为15时,若PC<AC,以C为原点,AC、BC所在直线分别为x、y轴建立坐标系如图(2),抛物线C1过点A、D、B;
①点Q在抛物线C1上,且位于线段PB的下方,过点Q作QN⊥PB,垂足为点N,是否存在点Q,使得QN最长,若存在,请求出QN的长度和Q点坐标;若不存在,请说明理由;
②将抛物线C1绕原点C旋转180°,得到抛物线C2,当﹣2a≤x≤﹣a时(a>0),抛物线C2有最大值2a,求a值.
【分析】(1)①过点E作EH⊥BC于点H,先证明△PCB≌△BHE(AAS),EH=CB=6,即可得到答案;②CD=x,BD=6﹣x,即可得到S与x的函数关系式;
(2)①由题可知点A(0,6),点B(6,0),由S△BDE=18﹣3x,求得x的值,得到点D的坐标,设抛物线G1:y=ax2+bx+c,用待定系数法求出抛物线C1解析式,当Q与E重合,点E在抛物线上时,QN=BE取最大值,EH=6,即进一步即可得到QN的长度和Q点的坐标;②将抛物线C1绕原点C旋转180°,得到抛物线C2为y=﹣x2﹣7x﹣6,化为顶点式,求出顶点式,然后分情况讨论即可.
【解析】(1)①过点E作EH⊥BC于点H,如图,
∵∠PBE=90°,
∴∠PBC+∠CBE=90°,
∵∠ACB=90°,
∴∠CPB+∠PBC=90°,
∴∠CPB=∠CBE,
在△PCB 和△BHE中,
,
∴△PCB≌△BHE(AAS),
∴EH=CB=6,
∴点E到BC边的距离为6,
故答案为:6;
②∵CD=x,BD=6﹣x,
∴S△BDE=BD×EH=×(6﹣x)×6=18﹣3x,
故答案为:S=18﹣3x;
(2)①由题知点A(0,6),点B(6,0),
∵S△BDE=18﹣3x=15,
∴x=1,
∴点D的坐标是(1,0),
设抛物线C1:y=ax2+bx+c,
将点A、D、B的坐标分别代入得,
,
解得:
,
∴抛物线C1的解析式为:y=x2﹣7x+6,
当Q与E重合,点E在抛物线上时,QN=BE取最大值,
∵EH=6,
∴将y=﹣6代入抛物线得:﹣6=x2﹣7x+6,
解得:x1=3,x₂=4,
当x=3时,BH=6﹣3=3=PC,与题干PC<AC相矛盾,
故x=3舍去,
∴BH=6﹣4=2,
∴QN==2,
∴Q点的坐标为(4,﹣6),
∴QN的最大值为2,
故QN的长度为2,Q点的坐标是(4,﹣6);
②将抛物线C1绕原点C旋转180°,得到抛物线C2为y=﹣x2﹣7x﹣6,
∵y=﹣x2﹣7x﹣6=﹣(x+)2+,
∴抛物线C2的项点坐标为(﹣,),
当﹣2a≤﹣≤﹣a时,2a=,
解得:a=,
当﹣a<﹣时,即﹣2a≤x≤﹣a,在抛物线对称轴左侧,y随x的增大而增大,
∴当x=﹣a时,取最大值,
即﹣a2+7a﹣6=2a,
解得a1=2,a2=3均不在﹣a<﹣范围内,故均舍去,
当﹣2a>﹣时,即﹣2a≤x≤a,在抛物线对称轴右侧,y随x的增大而减小,
∴当x=﹣2a 时,取最大值,
即﹣4a2+14a﹣6=2a,
解得a=,
∵﹣2a>﹣,即0,
∴a=舍去,
∴a=,
∴a=或a=.
10. (2023•乳源县三模)如图,对称轴为直线x=﹣1的抛物线y=a(x﹣h)2+k(a≠0)图象与x轴交于点A、B(点A在点B的左侧),与y轴交于点C,其中点B的坐标为(2,0),点C的坐标为(0,4).
(1)求该抛物线的解析式;
(2)如图1,若点P为抛物线上第二象限内的一个动点,点M为线段CO上一动点,当△APC的面积最大时,求△APM周长的最小值;
(3)如图2,将原抛物线绕点A旋转180°,得新抛物线y',在新抛物线y'的对称轴上是否存在点Q使得△ACQ为等腰三角形?若存在,请直接写出点Q的坐标;若不存在,说明理由.
【分析】(1)根据对称轴为直线x=﹣1,可得h=﹣1,再把点(2,0),(0,4)代入解析式即可求解;
(2)过点P作AC的平行线PN,当直线PN与抛物线只有一个交点时,△APC面积最大,由此可对称点P的坐标;再根据轴对称最值问题可求出△APM周长的最小值;
(3)由(1)可得原抛物线的顶点坐标,由旋转的性质可得y′的顶点坐标,进而可求出y′的对称轴;则需要分类讨论①当AC=AQ时;②当CA=CQ时;③当QA=QC时,分别建立方程求解即可.
【解析】(1)∵抛物线y=a(x﹣h)2+k(a≠0)的对称轴为直线x=﹣1,
∴x=h=﹣1,
∵抛物线过点B(2,0),点C(0,4),
∴,
解得,
∴抛物线的解析式为:y=﹣(x+1)2+.
(2)由(1)知函数解析式为:y=﹣(x+1)2+.
∴A(﹣4,0),
∴直线AC:y=x+4,
过点P作PN∥AC,设直线PN的解析式为:y=x+m,
当△APC的面积最大时,直线PN与抛物线有且仅有一个交点,
令x+m=﹣(x+1)2+,整理得x2+4x+2m﹣8=0,
∴Δ=42﹣4(2m﹣8)=0,解得m=6,
∴x2+4x+4=0,
∴x=﹣2,即P(﹣2,4);
作点A关于y轴的对称点A′,连接A′P交y轴于点M,如图1,此时△APM的周长最小,
∵A(﹣4,0),
∴A′(4,0),
∴A′P==2,AP==2,
∴△APM周长的最小值为:2+2.
(3)由(1)知原抛物线的顶点坐标D(﹣1,),绕点A旋转后的顶点D′(﹣7,﹣),
∴y′的对称轴为直线x=﹣7;
设点Q的坐标为(﹣7,t),
若△ACQ是等腰三角形,则需要分类讨论:
①当AC=AQ时,如图2;
∴(﹣4﹣0)2+(0﹣4)2=(﹣4+7)2+(0﹣t)2,解得t=±;
∴Q(﹣7,)或(﹣7,﹣);
②当CA=CQ时;
∴(﹣4﹣0)2+(0﹣4)2=(0+7)2+(4﹣t)2,无解;
③当QA=QC时,如图3,
∴(﹣4+7)2+(0﹣t)2=(0+7)2+(4﹣t)2,解得t=7,
∴Q(﹣7,7).
综上可知,存在,点Q的坐标为(﹣7,)或(﹣7,﹣)或(﹣7,7).
11. (2023秋•亭湖区期末)如图,在平面直角坐标系中,抛物线y=x2+bx+c经过点A(0,﹣3),与x轴的交点为B、C,直线l:y=2x+2与抛物线相交于点C,与y轴相交于点D,P是直线l下方抛物线上一动点.
(1)求抛物线的函数表达式;
(2)过点P作线段PM∥x轴,与直线l相交于点M,当PM最大时,求点P的坐标及PM的最大值;
(3)把抛物线绕点O旋转180°,再向上平移使得新抛物线过(2)中的P点,E是新抛物线与y轴的交点,F为原抛物线对称轴上一点,G为平面直角坐标系中一点,直接写出所有使得以B、E、F、G为顶点、BF为边的四边形是菱形的点G的坐标,并把求其中一个点G的坐标的过程写出来.
【分析】(1)先求出C点坐标为(﹣1,0),再把4(0,﹣3),C (﹣1,0)代入函数解析式y=x2+bx+c,求解即可;
(2)设P(a,a2﹣2a﹣3),因为PM∥x轴且点M在直线l:y=2x+2上,所以M(a2﹣a﹣,a2﹣2a﹣3),则PM=a﹣(a2﹣a﹣)=﹣a2+2a+=﹣(x﹣2)2+,再根据二次函数的最值求法求解即可;
(3)因为抛物线的函数表达式y=x2﹣2x﹣3,所以顶点坐标(1,﹣4),与x轴的交点B (3,0),C (﹣1,0),由旋转可得,新抛物线的项点为(﹣1,4),与x轴的交点为(﹣3,0),(1,0),所以设新抛物线解析式为y=﹣(x+1)2+4,因为向上平移使得新抛物线过(2)中的P (2,﹣3)点,设平移后解析式为y=﹣(x+1)2+4+k,所以3=﹣(2+1)2+4+k,解得k=2,所以平移后解析式为y=﹣(x+1)2+4+2=﹣x2﹣2x+5,所以E (0,5);设F(1,t),G(m,n),若以B、E、F、G为顶点,BF为边的四边形是菱形,则需要分线段BE是对角线或BE是边两种情况,分别根据菱形的性质求解即可.
【解析】(1)∵直线1:y=2x+2与抛物线相交于点C,
∴C点坐标为(﹣1,0),
把4(0,﹣3),C (﹣1,0)代入函数解析式y=x2+bx+c得:
,解得,
∴抛物线的函数表达式y=x2﹣2x﹣3.
(2)设P(a,a2﹣2a﹣3),
∵PM∥x轴,
∴M纵坐标为a2﹣2a﹣3,
∵点M在直线l:y=2x+2上,
∴M(a2﹣a﹣,a2﹣2a﹣3),
∴PM=a﹣(a2﹣a﹣)=﹣a2+2a+=﹣(x﹣2)2+,
∴当a=2时PM最大,最大值PM=,此时P点坐标(2,﹣3).
(3)∵抛物线的函数表达式y=x2﹣2x﹣3,
∴顶点坐标(1,﹣4),与x轴的交点B (3,0),C (﹣1,0),
∵把抛物线绕点O旋转180°,
∴旋转前后对应点关于原点对称,
∴新抛物线的项点为(﹣1,4),与x轴的交点为(﹣3,0),(1,0),
∴设新抛物线解析式为y=﹣(x+1)2+4,
∴向上平移使得新抛物线过(2)中的P (2,﹣3)点,
设平移后解析式为y=﹣(x+1)2+4+k,
∴3=﹣(2+1)2+4+k,解得k=2,
∴平移后解析式为y=﹣(x+1)2+4+2=﹣x2﹣2x+5,
∵E是平移后抛物线与y轴的交点,
∴E (0,5),
∵F为原抛物线对称轴上一点,G为平面直角坐标系中一点,
∴设F(1,t),G(m,n),
∵以B、E、F、G为顶点,BF为边的四边形是菱形,
∴线段BE可能是对角线也可能是边,
①当BE是对角线时,
∵菱形BFEG对角线BE,FG互相垂直平分,
∵E (0,5),B (3,0),
∴BE的中点坐标为(,),
∵BE的中点坐标也是FG的中点,
∴G (2,5﹣t),
∵GE=GB,
∴(2﹣0)2+(5﹣t﹣5)2=(2﹣3)2+(5﹣t﹣0)2,
解得:t=,即G点坐标(2,);
②当BE为边长时,BE=BF,
由距离公式得,(3﹣0)2+(0﹣5)2=(3﹣1)2+(0﹣t)2,
解得:t=±,
∵菱形BFGE对角线互相垂直平分,
∴由中点坐标公式可得,G(﹣2,+5)或(﹣2,﹣+5);
综上,满足题意的点G的坐标为:(﹣2,+5)或(﹣2,﹣+5)或(2,).
12. (2023秋•北京期中)定义:如果抛物线C1的顶点在抛物线C2上,同时,抛物线C2的顶点在抛物线C1上,则称抛物线C1与C2关联.例如,如图,抛物线y=x2的顶点(0,0)在抛物线y=﹣x2+2x上,抛物线y=﹣x2+2x的顶点(1,1)也在抛物线y=x2上,所以抛物线y=x2与y=﹣x2+2x关联.
(1)已知抛物线C1:y=(x+1)2﹣2,分别判断抛物线C2:y=﹣x2+2x+1和抛物线C3:y=2x2+2x+1与抛物线C1是否关联;
(2)抛物线M1:的顶点为A,动点P的坐标为(t,2),将抛物线M1绕点P(t,2)旋转180°得到抛物线M2,若抛物线M1与M2关联,求抛物线M2的解析式;
(3)抛物线M1:的顶点为A,点B是与M1关联的抛物线的顶点,将线段AB绕点A按顺时针方向旋转90°得到线段AB1,若点B1恰好在y轴上,请直接写出点B1的纵坐标.
【分析】(1)首先求得抛物线①的顶点坐标,然后检验是否此点在抛物线②与③上,再求得抛物线②的顶点坐标,检验是否在抛物线①上即可求得答案;
(2)首先求得抛物线M1的顶点坐标,则可得:点P在直线y=2上,则可作辅助线:作M关于P的对称点N,分别过点M、N作直线y=2的垂线,垂足为E,F,则可求得:点N的坐标,利用顶点式即可求得结果;
(3)根据全等三角形的知识,即可求得点B的坐标,从而求得B1点的坐标.
【解析】(1)∵抛物线C1:y=(x+1)2﹣2的顶点坐标为M(﹣1,﹣2),
∴当x=﹣1时,y=﹣x2+2x+1=﹣1﹣2+1=﹣2,
∴C1的顶点在抛物线C2上;
∵抛物线C2:y=﹣x2+2x+1=﹣(x﹣1)2+2,其顶点坐标为(1,2),
当x=1时,y=(x+1)2﹣2=22﹣2=2,
∴C2的顶点在抛物线C1上;
∴抛物线C1、C2是关联的;
∵抛物线C3:y=2x2+2x+1的顶点坐标为M(﹣,),
∴当x=﹣时,y=(x+1)2﹣2=﹣2=﹣,
∴抛物线C1与C3不关联;
综上,抛物线C1、C2是关联的;抛物线C1与C3不关联;
(2)抛物线M1:y=(x+1)2﹣2的顶点M的坐标为(﹣1,﹣2),
∵动点P的坐标为(t,2),
∴点P在直线y=2上,
作M关于P的对称点N,分别过点M、N作直线y=2的垂线,垂足为E,F,则ME=NF=4,
∴点N的纵坐标为6,
当y=6时,(x+1)2﹣2=6,
解得:x1=7,x2=﹣9,
①设抛物M2的解析式为:y=a(x﹣7)2+6,
∵点M(﹣1,﹣2)在抛物线M2上,
∴﹣2=a(﹣1﹣7)2+6,
∴a=﹣.
∴抛物线M2的解析式为:y=﹣(x﹣7)2+6;
②设抛物M2的解析式为:y=a(x+9)2+6,
∵点M(﹣1,﹣2)在抛物线M2上,
∴﹣2=a(﹣1+9)2+6,
∴a=﹣.
∴抛物线M2的解析式为:y=﹣(x+9)2+6;
(3)若A为抛物线M1:y=(x+1)2﹣2的顶点,
∴A(﹣1,﹣2),
当点B1恰好在y轴上,过A作x轴的平行线AN交y轴于N,过B作BM⊥AN于M,如图,
∴AN=1,
∵BA⊥B1A,
∴∠BAM+∠B1AN=90°,
∵∠BAM+∠ABM=90°,
∴∠ABM=∠B′AN,
∵AB=AB′,
∴△ABM≌△B1AN(AAS),
∴BM=AN=1,AM=B1N,
∴B点的纵坐标为﹣1,
把y=﹣1代入y=(x+1)2﹣2
解得:x=﹣1+2或x=﹣1﹣2,
∴B1(0,2﹣2)或(0,﹣2﹣2),
∴点B1的纵坐标是(0,2﹣2)或(0,﹣2﹣2).
13. (2023•锡山区一模)如图,抛物线y=x2+bx+c的顶点为M,对称轴是直线x=1,与x轴的交点为A(﹣3,0)和B,将抛物线y=x2+bx+c绕点B逆时针方向旋转90°,点M1、A1为点M、A旋转后的对应点,旋转后的抛物线与y轴相交于C,D两点.
(1)写出点B的坐标及求原抛物线的解析式;
(2)求证A,M,A1三点在同一直线上;
(3)设点P是旋转后抛物线上DM1之间的一动点,是否存在一点P,使四边形PM1MD的面积最大?如果存在,请求出点P的坐标及四边形PM1MD的面积;如果不存在,请说明理由.
【分析】(1)利用A坐标和A、B关于直线x=1对称求得点B坐标,即能用交点式表示抛物线解析式,再化简为一般式.
(2)求点M坐标和直线AM解析式;利用旋转求点A1坐标,把A1横坐标代入直线AM解析式求得y的值与A1总坐标相等,即点A1在直线AM上,得证.
(3)设点P(s,t)在旋转前对应点E,分别过点E、P作x轴垂线EG、PH,构造△BEG≌△PBH,由对应边相等推得点E坐标为(5+t,5﹣s),代回原抛物线解析式得到s与t的关系式.点D即s=0时,求得t=﹣10,点M即5+t=1,5﹣s=﹣4求得M1(9,﹣4),即MM1∥x轴.把四边形PM1MD分成△M1MD和△PM1D求面积和,其中△M1MD面积固定;PH与M1D交于点Q,则△PM1D面积等于PQ与点M1横坐标的积的一半.把前面所求s与t的关系书代入PQ的式子,即得到四边形PM1MD面积与t的二次函数关系,求得顶点式且顶点横坐标在可取值范围内,即求得P的坐标和面积最大值.
【解析】(1)∵原抛物线与x轴的交点为A(﹣3,0)和B
∴点A、B关于对称轴:直线x=1对称
∴点B坐标(5,0)
∴原抛物线解析式为y=(x+3)(x﹣5)=x2﹣x﹣
(2)证明:∵y=x2﹣x﹣=(x﹣1)2﹣4
∴M(1,﹣4)
设直线AM解析式为y=kx+a
∴ 解得:
∴直线AM解析式为y=﹣x﹣3
∵点A绕点B逆时针方向旋转90°得点A1
∴A1B=AB=5﹣(﹣3)=8,∠ABA1=90°
∴A1B⊥x轴,即xA1=xB=5
∴A1(5,﹣8)
当x=5时,y=﹣x﹣3=﹣5﹣3=﹣8
∴点A1在直线AM上
∴A,M,A1三点在同一直线上
(3)设原抛物线上的点E经旋转后为新抛物线上的点P,P在抛物线上DM1之间,如图1,
连接BE、BP、DM1,过点E作EG⊥x轴于点G,过点P作PH⊥x轴于点H,交DM1于点Q
∴∠EBP=∠EGB=∠BHP=90°,BE=BP
∴∠EBG+∠HBP=∠EBG+∠GEB=90°
∴∠HBP=∠GEB
在△BEG与△PBH中
∴△BEG≌△PBH(AAS)
∴EG=BH,BG=PH
设P(s,t)(s≥0,t<0)
∴BG=PH=﹣t,EG=BH=|s﹣5|
∴xE=5﹣(﹣t)=5+t
当s≤5时,EG=BH=5﹣s,点E在x轴上方
∴yE=5﹣s
当s>5时,EG=BH=s﹣5,点E在x轴下方
∴yE=﹣(s﹣5)=5﹣s
∴点E(5+t,5﹣s)在原抛物线上
∴(5+t)2﹣(5+t)﹣=5﹣s
整理得:s=﹣t2﹣2t+5
当s=0时,﹣t2﹣2t+5=0,解得:t1=2,t2=﹣10
∴D(0,﹣10)
∵M(1,﹣4)即
解得: 即点M1(9,﹣4)
∴MM1∥x轴,MM1=8,0≤s≤9,﹣10≤t≤﹣4
∴直线DM1解析式为y=x﹣10
∴Q(s,s﹣10)
∴PQ=s﹣10﹣t=(﹣t2﹣2t+5)﹣10﹣t=﹣t2﹣t﹣
∴S四边形PM1MD=S△M1MD+S△PM1D=M1M•(yM﹣yD)+PQ•(xM1﹣xD)=×8×6+(﹣t2﹣t﹣)=﹣t2﹣t﹣6=﹣(t+7)2+
∴当t=﹣7时,Smax=
∴s=﹣t2﹣2t+5=﹣×49﹣2×(﹣7)+5=
∴点P坐标为(,﹣7)使四边形PM1MD的面积最大,最大值为.
14. (2023秋•道里区校级期中)如图,在平面直角坐标系中,点O为坐标原点,直线y=x+3交x轴于点A,y轴于点D,抛物线y=x2+bx﹣3与x轴交于A,B两点,交y轴于点C.
(1)求抛物线的解析式;
(2)P在第三象限抛物线上,P点横坐标为t,连接AP、DP,△APD的面积为s,求s关于t的函数关系式;(不要求写自变量t的取值范围)
(3)在(2)的条件下,PD绕点P逆时针旋转,与线段AD相交于点E,且∠EPD=2∠PDC,过点E作EF⊥PD交PD于G,y轴于点F,连接PF,若,求线段PF的长.
【分析】(1)直接把A点坐标代入y=x2+bx﹣3求出b的值即可得到抛物线解析式为y=x2+2x﹣3;
(2)连接OP,过点P作PH⊥x轴于H,PN⊥y轴于N,根据s=S△APD=S△OAD+S△OAP﹣S△OPD可得出s与t的函数关系式;
(3)过D作DH⊥y轴交PE的延长线于H,作PM⊥DH于M,PN⊥y轴于N,如图3,利用PM∥DN得到∠PDC=∠DPM,加上∠EPD=2∠PDC,则∠HPM=∠DPM,于是根据等腰三角形的性质可得MH=MD,接着判断四边形PNDM为矩形得到MD=PN,则DH=2PN,然后证明△DEH≌△DEF得到DH=DF,所以DF=2MD=2PN;再在Rt△PFN中利用正弦定义可得到PF=3PN,利用勾股定理得FN=PN,设P点坐标为(t,t2+2t﹣3),则DF=﹣2t,FN=﹣2t,于是可表示出ON=DF+FN﹣OD=﹣2t﹣2t﹣3,所以﹣2t﹣2t﹣3=﹣(t2+2t﹣3),解方程得到得t1=﹣,t2=3(舍去),所以PF=3PN=3.
【解析】(1)∵直线y=x+3交x轴于点A,y轴于点D,
∴A(﹣3,0),D(0,3),
将A(﹣3,0)代入抛物线y=x2+bx﹣3,
∴(﹣3)2﹣3b﹣3=0,
∴b=2,
∴抛物线解析式为y=x2+2x﹣3,
(2)连接OP,过点P作PH⊥x轴于H,PN⊥y轴于N,
∵P在第三象限抛物线上,P点横坐标为t(t<0),
∴P(t,t2+2t﹣3),
∴s=S△APD=S△OAD+S△OAP﹣S△OPD
=
=
=
=﹣t2﹣t+9.
(3)过D作DH⊥y轴交PE的延长线于H,作PM⊥DH于M,PN⊥y轴于N,如图3,
∵PM∥DN,
∴∠PDC=∠DPM,
∵∠EPD=2∠PDC,
∴∠HPM=∠DPM,
而PM⊥DH,
∴MH=MD,
易得四边形PNDM为矩形,
∴MD=PN,
∴DH=2PN,
∵EF⊥PD,
∴∠GDF+∠DFG=90°,
而∠PHD+∠HPM=90°,
∴∠DFG=∠PHM,
∵∠ADF=45°,
∴∠HDE=45°,
∴△DEH≌△DEF(AAS),
∴DH=DF,
∴DF=2MD=2PN,
在Rt△PFN中,∵,
∴PF=3PN,
∴PN,
∴设P点坐标为(t,t2+2t﹣3),则DF=﹣2t,FN=﹣2t,
∴ON=DF+FN﹣OD=﹣2t﹣2t﹣3,
∴﹣2t﹣2t﹣3=﹣(t2+2t﹣3),
整理得t1=﹣,t2=3(舍去),
∴PF=3PN=﹣3t=3.
15. (2023秋•大兴区期中)在平面直角坐标系xOy中,已知四边形OABC是平行四边形,点A(4,0),∠AOC=60°,点C的纵坐标为,点D是边BC上一点,连接OD,将线段OD绕点O逆时针旋转60°得到线段OE.
给出如下定义:
如果抛物线y=ax2+bx(a≠0)同时经过点A,E,则称抛物线y=ax2+bx(a≠0)为关于点A,E的“伴随抛物线”.
(1)如图1,当点D与点C重合时,点E的坐标为 (﹣1,) ,此时关于点A,E的“伴随抛物线”的解析式为 y=x2﹣ ;
(2)如图2,当点D在边BC上运动时,连接CE.
①当CE取最小值时,求关于点A,E的“伴随抛物线”的解析式;
②若关于点A,E的“伴随抛物线”y=ax2+bx(a≠0)存在,直接写出a的取值范围.
【分析】(1)如图,连接CE,过点E作E′作x轴的垂线于点E′,由旋转可知,△COE是等边三角形,则∠EOE′=60°,解直角三角形可得到点E的坐标,将A,E的坐标代入抛物线解析式可得出结论;
(2)①由旋转可知,点E在线段C′B′上运动,过点C作CE⊥C′B′于点E,点E即为所求,过点E作y轴的垂线,过点C′作x轴的垂线,交EM于点M,交x轴于点N,
②过点B′作x轴的平行线,交MN于点P,由此可求出点B′的坐标,将点B′的坐标代入抛物线的解析式,即可得出a的最小值;由此可得出a的取值范围.
【解析】(1)如图,连接CE,过点E作E′作x轴的垂线于点E′,过点C作CC′⊥x轴于点C′,
∴CC′=,
∵∠AOC=60°,
∴OC=2,
由旋转可知,OE=OC=2,∠EOC=60°,
∴△COE是等边三角形,
∴∠EOE′=60°,
∴OE′=1,EE′=,
∴E(﹣1,).
将A(4,0),E(﹣1,)代入抛物线y=ax2+bx(a≠0),
∴,
解得.
∴抛物线的解析式为:y=x2﹣;
故答案为:(﹣1,);y=x2﹣;
(2)①由旋转可知,点E在线段C′B′上运动,过点C作CE⊥C′B′于点E,点E即为所求,过点E作y轴的垂线,过点C′作x轴的垂线,交EM于点M,交x轴于点N,
由题意可知,CC′=2,
由旋转可知,△OBC≌△OB′C′,
∴C′B′=CB=OA=4,∠OCB=∠OC′′=120°,
∵∠OC′C=60°,
∴∠B′C′C=60°,CC′=OC=2,
∴C′E=1,CE=,
∴ME=,C′M=,
∴E(﹣,).
将A(4,0),E(﹣,)代入抛物线y=ax2+bx(a≠0),
∴,
解得.
∴关于点A,E的“伴随抛物线”的解析式为:y=x2﹣.
②如图,过点B′作x轴的平行线,交MN于点P,
∴B′P=2,PC′=2,
∴B′(1,3),
将B′(1,3),A(4,0)代入抛物线的解析式y=ax2+bx(a≠0),
∴,
解得.
∴抛物线的解析式为:y=﹣x2+4.
结合图象可知,a的取值范围为:<a<;﹣<a<0.
16. (2023秋•天心区期末)如图1,在平面直角坐标系xOy中,抛物线C:y=﹣x2+bx+c与x轴相交于A,B两点,顶点为D,其中A(﹣4,0),B(4,0),设点F(m,0)是x轴的正半轴上一点,将抛物线C绕点F旋转180°,得到新的抛物线C'.
(1)求抛物线C的函数解析式;
(2)若抛物线C'与抛物线C在y轴的右侧有两个不同的公共点,求m的取值范围;
(3)如图2,P是第一象限内抛物线C上一点,它到两坐标轴的距离相等,点P在抛物线C'上的对应点P',设M是C上的动点,N是C'上的动点,试探究四边形PMP'N能否成为正方形?若能,求出m的值;若不能,请说明理由.
【分析】(1)运用待定系数法将A(﹣4,0),B(4,0),代入y=﹣x2+bx+c中,即可求得答案;
(2)设抛物线C′的解析式为:y=(x﹣2m)2﹣8,联立方程组,可得,由抛物线C′与抛物线C在y轴的右侧有两个不同的公共点,得出,解不等式组即可求得答案;
(3)如图2,作PE⊥x轴于E,MH⊥x轴于H.利用AAS证明△PFE≌△FMH,进而得出M(m+4,m﹣4),根据点M在y=﹣x2+8上,建立方程求解即可.
【解析】(1)由题意把点A(﹣4,0),B(4,0),代入y=﹣x2+bx+c中,
得:,
解得:,
∴抛物线C的函数解析式为:y=﹣x2+8;
(2)如图1,由题意抛物线C′的顶点坐标为(2m,﹣8),
设抛物线C′的解析式为:y=(x﹣2m)2﹣8,
由,
消去y得到:,
∵抛物线C′与抛物线C在y轴的右侧有两个不同的公共点,
∴,
解得:,
∴满足条件的m的取值范围为:4<m<4;
(3)结论:四边形PMP'N能成为正方形.
理由:情形1,如图2,作PE⊥x轴于E,MH⊥x轴于H.
由题意易知P(4,4),
当△PFM是等腰直角三角形时,四边形PMP'N是正方形,
∴PF=FM,∠PFM=90°,
∵∠PEF=∠FHM=90°,
∴∠PFE+∠FPE=90°,∠PFE+∠MFH=90°,
在△PFE和△FMH中,
∴,
∴△PFE≌△FMH(AAS),
∴PE=FH=4,EF=HM=4﹣m,
∴M(m+4,m﹣4),
∵点M在y=﹣x2+8上,
∴m﹣4=﹣(m+4)2+8,
解得或(舍),
∴m=﹣6+2时,四边形PMP'N是正方形.
情形2,如图,四边形PMP′N是正方形,同法可得M(m﹣4,4﹣m),
把M(m﹣4,4﹣m)代入y=﹣x2+8中,4﹣m=﹣(m﹣4)2+8,
解得m=12或m=0(舍去),
∴m=12时,四边形PMP′N是正方形.
综上,四边形PMP′N能成为正方形,m=﹣6+2或12.
17. (2023•大庆模拟)如图1,在平面直角坐标系xOy中,直线l:与x轴、y轴分别交于点A和点B(0,﹣1),抛物线经过点B,且与直线l的另一个交点为C(4,n).
(1)求n的值和抛物线的解析式;
(2)点D在抛物线上,且点D的横坐标为t(0<t<4).DE∥y轴交直线l于点E,点F在直线l上,且四边形DFEG为矩形(如图2).若矩形DFEG的周长为p,求p与t的函数关系式以及p的最大值;
(3)M是平面内一点,将△AOB绕点M沿逆时针方向旋转90°后,得到△A1O1B1,点A、O、B的对应点分别是点A1、O1、B1.若△A1O1B1的两个顶点恰好落在抛物线上,请直接写出点A1的横坐标.
【分析】(1)把点B的坐标代入直线解析式求出m的值,再把点C的坐标代入直线求解即可得到n的值,然后利用待定系数法求二次函数解析式解答;
(2)令y=0求出点A的坐标,从而得到OA、OB的长度,利用勾股定理列式求出AB的长,然后根据两直线平行,内错角相等可得∠ABO=∠DEF,再解直角三角形用DE表示出EF、DF,根据矩形的周长公式表示出p,利用直线和抛物线的解析式表示DE的长,整理即可得到P与t的关系式,再利用二次函数的最值问题解答;
(3)根据逆时针旋转角为90°可得A1O1∥y轴时,B1O1∥x轴,然后分①点O1、B1在抛物线上时,表示出两点的横坐标,再根据纵坐标相同列出方程求解即可;②点A1、B1在抛物线上时,表示出点B1的横坐标,再根据两点的纵坐标相差A1O1的长度列出方程求解即可.
【解析】(1)∵直线l:y=x+m经过点B(0,﹣1),
∴m=﹣1,
∴直线l的解析式为y=x﹣1,
∵直线l:y=x﹣1经过点C(4,n),
∴n=×4﹣1=2,
∵抛物线y=x2+bx+c经过点C(4,2)和点B(0,﹣1),
∴,
解得,
∴抛物线的解析式为y=x2﹣x﹣1;
(2)令y=0,则x﹣1=0,
解得x=,
∴点A的坐标为(,0),
∴OA=,
在Rt△OAB中,OB=1,
∴AB===,
∵DE∥y轴,
∴∠ABO=∠DEF,
在矩形DFEG中,EF=DE•cs∠DEF=DE•=DE,
DF=DE•sin∠DEF=DE•=DE,
∴p=2(DF+EF)=2(+)DE=DE,
∵点D的横坐标为t(0<t<4),
∴D(t,t2﹣t﹣1),E(t,t﹣1),
∴DE=(t﹣1)﹣(t2﹣t﹣1)=﹣t2+2t,
∴p=×(﹣t2+2t)=﹣t2+t,
∵p=﹣(t﹣2)2+,且﹣<0,
∴当t=2时,p有最大值;
(3)∵△AOB绕点M沿逆时针方向旋转90°,
∴A1O1∥y轴时,B1O1∥x轴,设点A1的横坐标为x,
①如图1,点O1、B1在抛物线上时,点O1的横坐标为x,点B1的横坐标为x+1,
∴x2﹣x﹣1=(x+1)2﹣(x+1)﹣1,
解得x=,
②如图2,点A1、B1在抛物线上时,点B1的横坐标为x+1,点A1的纵坐标比点B1的纵坐标大,
∴x2﹣x﹣1=(x+1)2﹣(x+1)﹣1+,
解得x=﹣,
综上所述,点A1的横坐标为或﹣.
18. (2023•苏州一模)如图,二次函数y=x2+bx+4的图象与x轴交于点A、B,与y轴交于点C,点A的坐标为(﹣8,0),P是抛物线上一点(点P与点A、B、C不重合).
(1)b= ﹣ ,点B的坐标是 (3,0) ;
(2)连接AC、BC,证明:∠CBA=2∠CAB;
(3)点D为AC的中点,点E是抛物线在第二象限图象上一动点,作DE,把点A沿直线DE翻折,点A的对称点为点G,点E运动时,当点G恰好落在直线BC上时,求E点的坐标.
【分析】(1)利用待定系数法解答即可;
(2)连接AC,BC,在OA上截取OD=OB,连接CD,利用线段垂直平分线的性质,等腰三角形的性质和三角形的外角等于和它不相邻的两个内角的和解答即可;
(2)依题意画出图形,连接DG,利用如果一个三角形一条边上的中线等于这边的一半,那么这个三角形是直角三角形得到AG⊥BC,利用待定系数法求得直线BC的解析式,进而得到直线DE的解析式,将直线DE的解析式与抛物线解析式联立即可求得点E坐标.
【解答】(1)解:∵二次函数y=x2+bx+4的图象与x轴交于点A(﹣8,0),
∴﹣+4=0,
解得:b=﹣.
∴抛物线的解析式为:y=﹣x+4.
令y=0,则﹣x+4=0,
解得:x=﹣8或3,
∴B(3,0).
故答案为:﹣;(3,0);
(2)证明:连接AC,BC,在OA上截取OD=OB,连接CD,如图,
∵A(﹣8,0),B(3,0),
∴OA=8,OB=3,
∴OD=OB=3,
∴CO是BD的垂直平分线,
∴BC=CD.
∴∠CBA=∠CDB.
令x=0,则y=4,
∴OC=4,
∴CD==5.
∵AD=OA﹣OD=8﹣3=5,
∴AD=DC,
∴∠BAC=∠ACD.
∵∠CDB=∠BAC+∠ACD,
∴∠CDB=2∠BAC,
∴∠CBA=2∠CAB;
(3)解:连接DG,如图,
∵点D为AC的中点,
∴D(﹣4,2),AD=CD.
∵把点A沿直线DE翻折,点A的对称点为点G,
∴DG=DA,
∴DG=AD=DC,
∴∠AGC=90°,
∴AG⊥BC.
设直线BC的解析式为y=kx+n,
∴,
解得:,
∴直线BC的解析式为y=x+4.
设直线DE的解析式为y=x+m,
∴﹣×(﹣4)+m=2,
∴m=﹣.
∴直线DE的解析式为y=x﹣.
∴.
解得:x=.
∵点E是抛物线在第二象限图象上一动点,
∴x=.
∴y=,
∴E(,).
19. (2023•大连模拟)已知抛物线G:y=(m+1)x2+2(n﹣1)x+n+1(m≠﹣1,m为常数)的对称轴与直线y=kx+k(k>0,k为常数)相交于x轴上一点P.
(1)求m与n的数量关系;
(2)若直线y=kx+k与y轴交于点Q,且OQ=OP,
①把直线y=kx+k绕点Q顺时针旋转45°得到的直线与抛物线G相交于A、B两点,若AB=4,求m的值;
②将直线y=kx+k向上平移2k个单位,得到的直线与抛物线G的两个交点的横坐标x1,x2满足﹣2<x1<x2<2,求m的取值范围.
【分析】(1)由题意可知对称轴为直线x==﹣1,即可求m、n的关系;
(2)①由条件求出k的值,在求出旋转后直线的解析式为y=1,由题意可得1=(m+1)x2+2(n﹣1)x+n+1,利用根与系数的关系求出AB=4=,求出n的值即可求m的值;
②先求出平移后直线的解析式,由x+3=(m+1)x2+2(n﹣1)x+n+1,解得x=﹣1或x=﹣,当m+1>0时,x1=﹣1,x2=﹣,则﹣1<﹣<2,解得m>﹣;当m+1<0时,x1=﹣,x2=﹣1,则﹣2<﹣<﹣1,解得m<﹣2.
【解析】(1)y=(m+1)x2+2(n﹣1)x+n+1的对称轴为直线x=﹣=,
∵直线y=kx+k与x轴的交点为(﹣1,0),
∴=﹣1,
∴n﹣m=2;
(2)①y=kx+k与y轴交于点Q(0,k),
∵OQ=OP,
∴k=1,
∴Q(0,1),
∵直线y=x+1绕点Q顺时针旋转45°,
∴直线y=x+1旋转后的直线为y=1,
∵直线y=1与抛物线G相交于A、B两点,
∴1=(m+1)x2+2(n﹣1)x+n+1,
∵n﹣2=m,
∴(n﹣1)x2+2(n﹣1)x+n=0,
∴xA+xB=﹣2,xA•xB=,
∵AB=4,
∴4=,
解得n=,
∴m=﹣;
②直线y=x+1向上平移2个单位后得到y=x+3,
∵直线与抛物线有两个交点,
∴x+3=(m+1)x2+2(n﹣1)x+n+1,
∵n=m+2,
∴(m+1)x2+(2m+1)x+m=0,
∴x=﹣1或x=﹣,
当m+1>0时,x1=﹣1,x2=﹣,
∵﹣2<x1<x2<2,
∴﹣1<﹣<2,
解得m>﹣;
当m+1<0时,x1=﹣,x2=﹣1,
∵﹣2<x1<x2<2,
∴﹣2<﹣<﹣1
解得m<﹣2;
综上所述:m<﹣2或m>﹣.
20. (2023•兰州)如图1,二次函数y=a(x+3)(x﹣4)图象交坐标轴于点A,B(0,﹣2),点P为x轴上一动点.
(1)求二次函数y=a(x+3)(x﹣4)的表达式;
(2)过点P作PQ⊥x轴分别交线段AB,抛物线于点Q,C,连接AC.当OP=1时,求△ACQ的面积;
(3)如图2,将线段PB绕点P逆时针旋转90°得到线段PD.当点D在抛物线上时,求点D的坐标.
【分析】(1)将B(0,﹣2)代入y=a(x+3)(x﹣4),即可求解;
(2)先求直线AB的解析式为y=x﹣2,则Q(1,﹣),C(1,﹣2),可求S△ACQ=S△ACP﹣S△APQ=;
(3)设P(t,0),过点D作x轴垂线交于点N,可证明△PND≌△BOP(AAS),则D(t+2,﹣t),将D点代入抛物线解析式得﹣t=(t+2+3)(t+2﹣4),求得D(3,﹣1)或D(﹣8,10).
【解析】(1)将B(0,﹣2)代入y=a(x+3)(x﹣4),
∴a=,
∴y=(x+3)(x﹣4)=x2﹣x﹣2;
(2)令y=0,则(x+3)(x﹣4)=0,
∴x=﹣3或x=4,
∴A(4,0),
设直线AB的解析式为y=kx+b,
∴,
∴,
∴y=x﹣2,
∵OP=1,
∴P(1,0),
∵PQ⊥x轴,
∴Q(1,﹣),C(1,﹣2),
∴AP=3,
∴S△ACQ=S△ACP﹣S△APQ=×3×2﹣×3×=;
(3)设P(t,0),
如图2,过点D作x轴垂线交于点N,
∵∠BPD=90°,
∴∠OPB+∠NPD=90°,∠OPB+∠OBP=90°,
∴∠NPD=∠OBP,
∵BP=PD,
∴△PND≌△BOP(AAS),
∴OP=ND,BO=PN,
∴D(t+2,﹣t),
∴﹣t=(t+2+3)(t+2﹣4),
解得t=1或t=﹣10,
∴D(3,﹣1)或D(﹣8,10).
2024年中考数学压轴题之学霸秘笈大揭秘专题15二次函数与角综合问题(原卷版+解析): 这是一份2024年中考数学压轴题之学霸秘笈大揭秘专题15二次函数与角综合问题(原卷版+解析),共107页。试卷主要包含了角的数量关系问题,角的最值问题等内容,欢迎下载使用。
中考数学压轴题之学霸秘笈大揭秘(全国通用)专题16二次函数与动点综合问题(全国通用)(原卷版+解析): 这是一份中考数学压轴题之学霸秘笈大揭秘(全国通用)专题16二次函数与动点综合问题(全国通用)(原卷版+解析),共80页。
中考数学压轴题之学霸秘笈大揭秘(全国通用)专题7二次函数与菱形存在性问题(原卷版+解析): 这是一份中考数学压轴题之学霸秘笈大揭秘(全国通用)专题7二次函数与菱形存在性问题(原卷版+解析),共104页。












