

重庆市沙坪坝区重点学校2023-2024学年七年级上学期期末数学试题(无答案)
展开一、选择题(本大题12个小题,每小题3分,共36分)在每个小题的下面,都给出了代号为A、B、C、D的四个答案,其中只有一个是正确的,请将答题卡对应的方框涂黑.
1.2024的相反数是( )
A.2024B.C.D.
2.五个大小相同的正方体搭成的几何体如图所示,从左面看到的图形是( )
A.B.C.D.
3.下列调查中,最适宜采用全面调查(普查)的是( )
A.调查全国中学生每天作业完成的时间
B.调查一批“遥遥领先”手机的电池寿命
C.调查我市中学生观看电影《流浪地球2》的情况
D.为保证全球首架C919大型客机首飞成功,对其零部件进行检查
4.下列各式成立的是( )
A.B.C.D.
5.已知,则下列变形中不成立的是( )
A.B.C.D.
6.如图所示,射线在射线的反向延长线上,则射线的方向是( )
A.北偏东65°B.东偏北65°C.北偏东75°D.东偏北75°
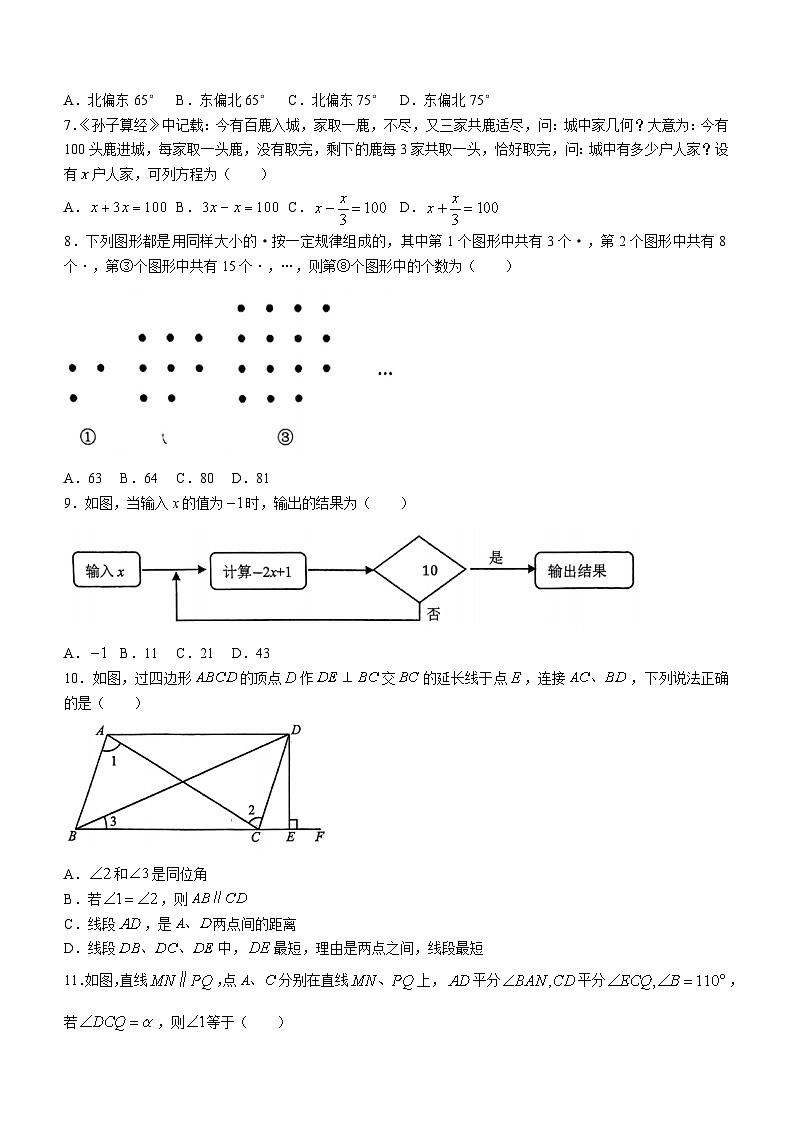
7.《孙子算经》中记载:今有百鹿入城,家取一鹿,不尽,又三家共鹿适尽,问:城中家几何?大意为:今有100头鹿进城,每家取一头鹿,没有取完,剩下的鹿每3家共取一头,恰好取完,问:城中有多少户人家?设有户人家,可列方程为( )
A.B.C.D.
8.下列图形都是用同样大小的·按一定规律组成的,其中第1个图形中共有3个·,第2个图形中共有8个·,第③个图形中共有15个·,…,则第⑧个图形中的个数为( )
A.63B.64C.80D.81
9.如图,当输入x的值为时,输出的结果为( )
A.B.11C.21D.43
10.如图,过四边形的顶点作交的延长线于点,连接,下列说法正确的是( )
A.和是同位角
B.若,则
C.线段,是两点间的距离
D.线段中,最短,理由是两点之间,线段最短
11.如图,直线,点分别在直线上,平分平分,若,则等于( )
A.B.C.D.
13.已知3个多项式分别为:,下列结论正确的个数有( )
①若,则;
②若的结果为单项式,则;
③若关于的方程无解,则;
④代数式化简后共有3种不同表达式.
A.1个B.2个C.3个D.4个
二、填空题(本大题14个小题,每空2分,共30分)请将每小题的答案直接填在答题卡对应的横线上.
13.单项式的系数为______.
14.2023年除夕之夜,盛大的光影焰火秀在重庆绽放,浪漫的山城以跨年焰火的形式辞旧迎新.据统计,近距离线下观看焰火秀的人数近590000人,将数据590000用科学记数法表示应为______.
15.已知是关于的方程的解,则的值为______.
16.若两个单项式与是同类项,则的值为______.
17.一个角的补角为,则这个角的度数为______.
18.如图,为线段的中点,若点在线段上,且,则线段的长为______.
19.如图,当钟表上的时间显示为7:20,时针与分针所成的夹角为______度.
20.艳艳和君君约定从地沿相同路线骑行去地,已知艳艳的速度是君君速度的1.2倍,若君君先骑行2千米,艳艳才从地出发,艳艳出发半小时后恰好追上君君,则君君每小时骑行______千米.
21.若,则代数式的值为______.
22.有理数在数轴上的对应点如图所示,化简:______.
23.如图,,连接,点在上,连接,已知平分,根据尺规所作出射线的痕迹,求为______度.
24.一个学习小组开展了“长方体纸盒的制作”实践活动.图①是一个正方形纸板,裁掉阴影部分后将其折叠成如图②所示的长方体盒子,已知该长方体的宽是高的2倍,长比高多,则这个正方形纸板的边长为______.
25.如图①,分别在上,平分,且.如图②,将绕点以的速度逆时针转动,将绕点以的速度逆时针转动,若它们同时开始转动,设转动时间为秒,当转至所在射线后,二者同时停止转动,则在旋转过程中,当与互相平行或垂直时,的值为______.
26.一个三位正整数,若百位上的数字与个位上的数字之和是十位上的数字的3倍,则称这个三位数为“3倍特征数”.例如:125满足,所以125是“3倍特征数”.对于某些“3倍特征数”,可进行如下操作:取相邻数位上的两个数的平均数放入这两个数之间,并去掉未取数位上的数字,得到两个新的三位数.并规定,且能被3整除,则满足题意的“3倍特征数”的值为______.
三、计算题(本大题4个小题,每小题8分,共32分)解答时每小题必须给出必要的演算过程,请将解答过程书写在答题卡中对应的位置上.
27.计算:
(1);(2).
28.合并同类项:
(1);(2).
29.解方程:
(1);(2).
30.先化简,再求值:,其中为的倒数,.
四、解答题(本大题5个小题,31-34每小题10分,35题12分,共52分)解答时每小题必须给出必要的演算过程或推理步骤,画出必要的图形(包括辅助线),请将解答过程书写在答题卡中对应的位置上.
31.如图,已知点在线段上,为直线外一点.
(1)请按要求进行尺规作图(不写作法,保留作图痕迹).
①连接;
②在线段上截取点,使得线段;
③若,在线段上取的中点.
(2)由于M为AB的中点,小敏在学习完线段中点的相关知识后,进行了自主研究,若N为AC的中点,则双中点M、N构成的线段MN与图中线段存在一定的关系,请根据她的思路,补全下列解题过程:
解:点是线段的中点,
①______
点是线段的中点,
∴②______
③______
即
④______.
32.重庆市北关中学七年级在本学期举行了速算比赛,为了解该年级525名学生的速算成绩分布情况,随机抽取了部分学生的速算成绩,根据成绩情况分为五组(成绩得分为百分制,用x表示):A组:,B组:,C组:,D组:,E组:,将调查的数据进行整理,绘制了如下两幅不完整的统计图。请根据以上信息,解答下列问题:
(1)此次调查的总体是______;(选填“A”或“B”)
A.525名学生B.525名学生的速算成绩
(2)此次调查的样本容量是______,在扇形统计图中D组所在扇形的圆心角为______度;
(3)请把频数直方图补充完整;
(4)请估计该校七年级速算成绩不低于80分的学生人数.
33.如图,平分为延长线上一点,连接,使,过作.
(1)求证:;
(2)若,求的度数.
34.小南计划安装如图所示由六块相同的长方形玻璃组成的窗户(如图①),该窗户长为6米,宽为a米(),玻璃上方安装了两张半径相同且不重叠的扇形遮光帘(如图②).
(1)该窗户的透光面积共______平方米;(用含a的代数式表示,结果保留)
(2)(列一元一次方程解决问题)安装一扇这样的窗户需要6块长方形玻璃,2张遮光帘,某厂家现有工人50人,平均每人每天可加工长方形玻璃8块或遮光帘4张,为了使每天的产品刚好配套,应该分配多少名工人生产长方形玻璃,多少名工人生产遮光帘?
(3)在同等质量的前提下,甲、乙两个厂家制作玻璃与遮光帘的收费方式如下:
若小南选择甲、乙两个厂家所需费用相同,求a的值.(在(3)小问中的取3)
35.如图①,在直角三角形中,.
(1)动点同时从出发,以每秒1个单位长度的速度沿折线方向运动,以每秒2个单位长度的速度沿折线方向运动,经过______秒两点首次相遇,相遇时它们距点______个单位长度;
(2)如图②,动点从出发,沿折线(含端点和)运动,速度为每秒2个单位长度,到达点停止运动,已知点到的距离为个单位长度,设点的运动时间为秒,当的面积为时,求的值;
(3)如图③,将三角形的顶点与数轴原点重合,将数轴正半轴部分沿折叠在三角形的两边上,得到一条“折线数轴”,在“折线数轴”上,把两点所对应的两数之差的绝对值叫这两点间的距离.例如,点和点在折线数轴上的距离为个单位长度.动点从点出发,以4个单位/秒的速度沿着折线数轴的正方向运动,从点运动到点期间速度变为原来的一半,过点后继续以原来的速度向数轴的正方向运动;与此同时,点从点出发,以2个单位/秒的速度沿着折线数轴的负方向运动,从点运动到点期间速度变为3.5个单位/秒,过点后继续以原来的速度向数轴的负方向运动,设运动时间为秒.在此运动过程中,两点的距离与两点的距离是否会相等?若相等,请直接写出的值;若不相等,请说明理由.
遮光帘(元/平方米)
玻璃(元/平方米)
甲厂家
40
不超过10平方米的部分,90元/平方米;
超过10平方米的部分,78元/平方米
乙厂家
50
85元/平方米,且每购买1平方米的玻璃赠送0.1平方米遮光帘
重庆市沙坪坝区南开中学校2023-2024学年七年级上学期期末数学试题: 这是一份重庆市沙坪坝区南开中学校2023-2024学年七年级上学期期末数学试题,共29页。
重庆市沙坪坝区2023-2024学年七年级上学期期末数学试题(含答案): 这是一份重庆市沙坪坝区2023-2024学年七年级上学期期末数学试题(含答案),共20页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。
重庆市沙坪坝区2023-2024学年七年级上学期期末数学试题: 这是一份重庆市沙坪坝区2023-2024学年七年级上学期期末数学试题,共6页。












