

吉林省长春市南关区2023-2024学年上学期七年级期末质量调研数学试卷
展开一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
1.−14的相反数是( )
A.−14B.4C.−4D.14
2.随着科学技术的不断提高,5G网络已经成为新时代的“宠儿”,预计到2025年,全球5G用户将达到1570000000人.将1570000000用科学记数法表示为( )
A.1.57×109B.1.57×107C.1.57×108D.157×109
3.下列单项式中,与−3ab2是同类项的是( )
A.−3ab3B.12ba2C.2ab2D.3a2b2
4.下列去括号正确的是( )
A.3a−(b−2c)=3a+b−2cB.3a−(b−2c)=3a−b−2c
C.−2a+3(b−1)=−2a+3b−1D.−2a+3(b−1)=−2a+3b−3
5.如所示四个图形中,不能作为正方体的展开图的是( )
A.B.
C.D.
6.将多项式3xy3−x2y3−9y+x3按x的升幂排列的结果是( )
A.x3−9y−x2y3+3xy3B.x3−x2y3+3xy3−9y
C.−9y+x3+3xy3−x2y3D.−9y+3xy3−x2y3+x3
7.如图,从A地到B地有三条路线,由上至下依次记为a、b、c,则从A地到B地的最短路径是b,其中蕴含的数学道理是( )
A.直线比曲线短B.两点确定一条直线
C.两点之间,线段最短D.经过一点有无数条直线
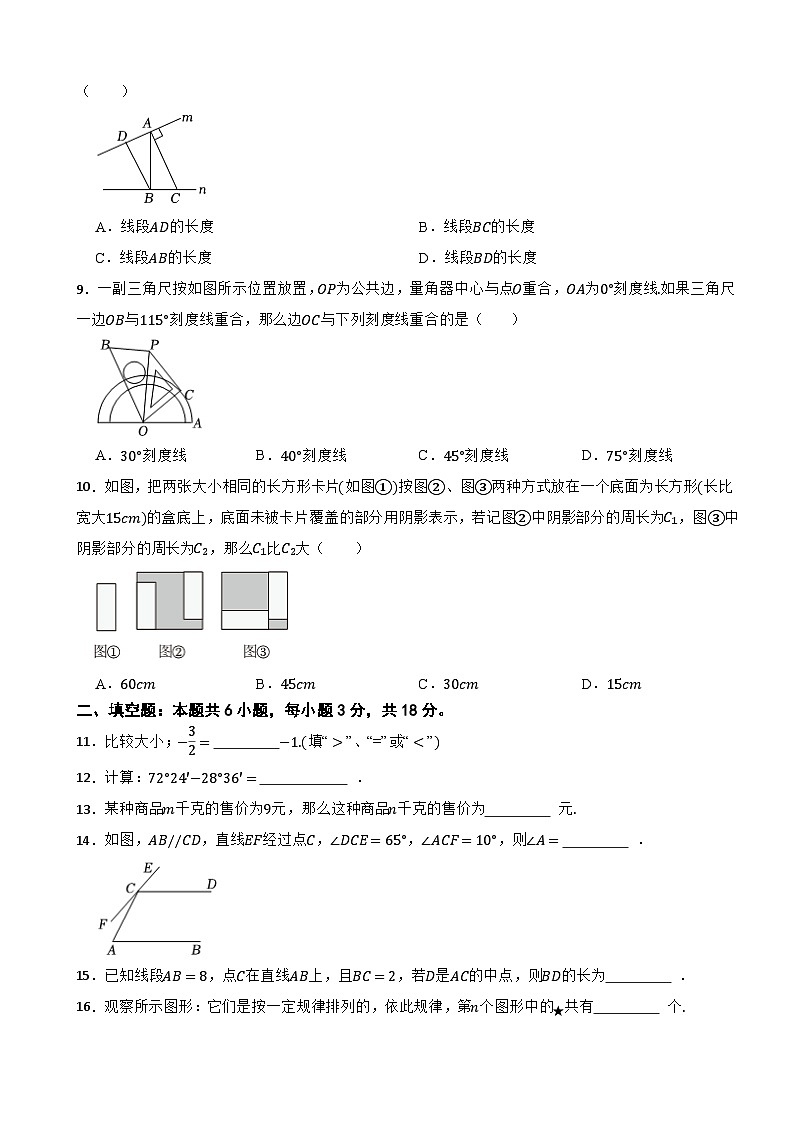
8.如图,点A,D在直线m上,点B,C在直线n上,AB⊥n,AC⊥m,BD⊥m,点A到直线BD的距离是( )
A.线段AD的长度B.线段BC的长度
C.线段AB的长度D.线段BD的长度
9.一副三角尺按如图所示位置放置,OP为公共边,量角器中心与点O重合,OA为0°刻度线.如果三角尺一边OB与115°刻度线重合,那么边OC与下列刻度线重合的是( )
A.30°刻度线B.40°刻度线C.45°刻度线D.75°刻度线
10.如图,把两张大小相同的长方形卡片(如图①)按图②、图③两种方式放在一个底面为长方形(长比宽大15cm)的盒底上,底面未被卡片覆盖的部分用阴影表示,若记图②中阴影部分的周长为C1,图③中阴影部分的周长为C2,那么C1比C2大( )
A.60cmB.45cmC.30cmD.15cm
二、填空题:本题共6小题,每小题3分,共18分。
11.比较大小;−32= −1.(填“>”、“=”或“<”)
12.计算:72°24'−28°36'= .
13.某种商品m千克的售价为9元,那么这种商品n千克的售价为 元.
14.如图,AB//CD,直线EF经过点C,∠DCE=65°,∠ACF=10°,则∠A= .
15.已知线段AB=8,点C在直线AB上,且BC=2,若D是AC的中点,则BD的长为 .
16.观察所示图形:它们是按一定规律排列的,依此规律,第n个图形中的★共有 个.
三、解答题:本题共12小题,共72分。解答应写出文字说明,证明过程或演算步骤。
17. 计算:−15−(+21)−(−8).
18. 计算:24÷(−6)×32÷(−43).
19. 计算:−52+2×(−3)2−(−8)÷(−113).
20. 计算:(5x−y)−3(2x−3y)+x.
21. 先化简,再求值:2ab2−[3a2b−2(3a2b−ab2−1)],其中a=−1,b=3.
22. 如图,是6×6的正方形网格,每个小正方形的顶点为格点,线段AB的两个端点及点C均在格点上.
(1)过点C作AB的垂线,垂足为点D;
(2)过点C作AB的平行线MN(点M、N在点C的异侧,点M在点N上方);
(3)E是线段AB与网格线的交点,连接CE、CB.
写出∠AEC的同旁内角 ;
写出与∠ABC相等的角 ;
比较线段的大小:CB CE,CD CE.(填“>”、“<”或“=”)
23. 如图,直线AB、CD相交于点O,OE平分∠AOD,OF⊥CD.若∠AOC=40°,求∠EOF的度数.
24.如图是长春市南北方向上地铁一号线的线路图,途中共设15个站点.某天,李华参加该线路上的志愿者服务活动,从北环城路站出发,最后在A站结束服务活动.如果规定向南为正,向北为负,李华当天乘坐地铁的站数按先后顺序依次记录如下(单位:站):+5,−2,+3,+1,+4,−2,+3,−4,−6.
(1)请通过计算说明A站是哪一站?
(2)若相邻两站之间的平均距离约为1.5千米,求这次李华志愿服务期间乘坐地铁行进的总路程约是多少千米?
25.如图,已知∠1=∠2,∠4=∠B,∠ADF=90°,求证:GF⊥BC.
阅读下面的解答过程,填空并填写理由.
证明:
∵∠4=∠B(已知),
∴AB// ( ).
∴∠2=∠3( )
∵∠1=∠2(已知),
∴∠1=∠3(等量代换).
∴AD// ( )
∴∠ADF+∠GFD= ( )
又∵∠ADF=90°(已知),
∴∠GFD=90°.
∴GF⊥BC.
26. 某学校为了全面提高学生的综合素养,开展了音乐、朗诵、舞蹈、美术共四个社团,学生积极参加(每个学生限报一项),参加社团的学生共有220人,其中音乐社团有a人参加,朗诵社团的人数比音乐社团人数的一半多b人,舞蹈社团的人数比朗诵社团人数的2倍少40人.
(1)参加朗诵社团有 人,参加舞蹈社团有 人.(用含a,b的式子表示)
(2)求美术社团有多少人?(用含a,b的式子表示)
(3)若a=60,b=25,求美术杜团的人数.
27.
(1)【猜想】如图①,AB//CD,点E在直线AB、CD之间,连结EB、ED.若∠B=25°,∠D=40°,则∠BED的大小为 度.
(2)【探究】如图②,AB//CD、BE、CE交于点E,探究∠E、∠B、∠C之间的数量关系.
(3)【拓展】如图③,AB//CD,BF、CG分别平分∠ABE和∠DCE,且BF、CG所在直线交于点F,过点F作FH//AB,若∠BEC=104°,则∠BFC= 度.
28.如图,点M、A、B、N由左至右依次均在数轴上,点A在原点,AB=3AM,AM=2BN,AB=30cm,点P从点M出发,沿MN方向以2cm/s的速度运动,同时点Q从点N出发沿NM方向向点M匀速运动(点Q运动到点M时停止运动),设运动的时间为t秒.
(1)点M表示的数是 ,点P表示的数是 .(点P用含t的代数式表示)
(2)点P在线段AB上,当PA=2PB时,点Q运动到的位置恰好是线段AB的中点,求点Q的运动速度.
(3)若点Q的运动速度为3cm/s,经过多长时间P、Q两点相距35cm?
答案解析部分
1.【答案】D
【知识点】实数的相反数
【解析】【解答】解:由题意得−14的相反数是14,
故答案为:D
【分析】根据题意结合相反数的定义即可得到−14的相反数,进而即可求解。
2.【答案】A
【知识点】科学记数法表示大于10的数
【解析】【解答】解:由题意得将1570000000用科学记数法表示为1.57×109,
故答案为:A
【分析】根据题意结合科学记数法表示数据1570000000即可求解。
3.【答案】C
【知识点】单项式的概念;同类项的概念
【解析】【解答】解:由题意得2ab2与−3ab2是同类项,
故答案为:C
【分析】根据同类项的定义结合题意对选项逐一分析即可得到2ab2与−3ab2是同类项。
4.【答案】D
【知识点】去括号法则及应用
【解析】【解答】解:
AB、3a−(b−2c)=3a−b+2c,AB不符合题意;
CD、−2a+3(b−1)=−2a+3b−3,C不符合题意,D符合题意;
故答案为:D
【分析】根据题意对选项逐一去括号即可得到3a−(b−2c)=3a−b+2c,−2a+3(b−1)=−2a+3b−3,进而即可求解。
5.【答案】B
【知识点】几何体的展开图
【解析】【解答】解:由题意得,,均可还原为正方体,可以作为正方体的展开图;不可还原为正方体,不能做完正方体的展开图,
故答案为:B
【分析】根据正方体的展开图结合题意对选项逐一分析即可求解。
6.【答案】D
【知识点】幂的排列;多项式的项、系数与次数
【解析】【解答】解:由题意得将多项式3xy3−x2y3−9y+x3按x的升幂排列的结果是−9y+3xy3−x2y3+x3,
故答案为:D
【分析】根据升幂的定义结合题意对多项式每一项进行排序,进而即可求解。
7.【答案】C
【知识点】线段的性质:两点之间线段最短
【解析】【解答】解:由题意得从A地到B地的最短路径是b,其中蕴含的数学道理是两点之间,线段最短,
故答案为:C
【分析】根据线段的定义:两点之间,线段最短,结合题意即可求解。
8.【答案】A
【知识点】点到直线的距离
【解析】【解答】解:由题意得∠ADB=90°,
∴点A到直线BD的距离是AD的长度,
故答案为:A
【分析】根据点到直线的距离结合题意即可得到点A到直线BD的距离是线段AD的长度。
9.【答案】B
【知识点】角的运算
【解析】【解答】解:由图可知∠BOP=30°,∠POC=45°,∠BOA=115°,
∴∠AOC=∠BOA−∠BOP−∠POC=115°−30°−45°=40°.
故答案为:B
【分析】由图可知∠BOP=30°,∠POC=45°,∠BOA=115°,进而结合题意进行角的运算即可求解。
10.【答案】C
【知识点】整式的混合运算;用代数式表示几何图形的数量关系
【解析】【解答】解:设大长方形的宽为a cm,则长为(a+15)cm,图①中的长方形长为x cm,宽为y cm,
图②中阴影部分的周长为C1为:2[(a+15)+a]=(4a+30)cm,
由图③可得,x+y=a+15,
图③中阴影部分的周长为C2为:2(a+15)+2(a−y)+2(a−x)=2(3a+15−x−y)=2(3a+15−a−15)=4a(cm),
(4a+30)−4a
=4a+30−4a
=30(cm),
即C1比C2大30cm,
故答案为:C
【分析】设大长方形的宽为a cm,则长为(a+15)cm,图①中的长方形长为x cm,宽为y cm,进而结合题意计算C1和C2即可求解。
11.【答案】<
【知识点】有理数的大小比较-直接比较法
【解析】【解答】解:由题意得−32<−1,
故答案为:<
【分析】根据题意直接比较有理数的大小即可得到−32<−1。
12.【答案】43°48'
【知识点】角的运算
【解析】【解答】解:由题意得72°24'−28°36'=43°48',
故答案为:43°48'
【分析】根据题意直接进行角的运算即可得到72°24'−28°36'=43°48'。
13.【答案】9nm
【知识点】用代数式表示实际问题中的数量关系
【解析】【解答】解:由题意得1kg这种商品的售价为9m元,
∴这种商品n千克的售价为9nm元,
故答案为:9nm
【分析】先根据题意得到1kg这种商品的售价,进而结合题意即可得到这种商品n千克的售价。
14.【答案】75°
【知识点】平行线的性质
【解析】【解答】解:由题意得∠DCA=180°-10°-65°=105°,
∵AB∥CD,
∴∠A+∠DCA=180°,
∴∠A=75°,
故答案为:75°
【分析】先根据平角得到∠DCA的度数,进而根据平行线的性质即可求解。
15.【答案】3或5
【知识点】线段的中点;线段的计算
【解析】【解答】解:分两种情况当点C在点B的右侧时,如图1:
∵AB=8,BC=2,
∴AC=CB+BA=10,
∵点D为的AC中点,
∴AD=5,
∴BD=AB−AD=3;
当点C在点B的左侧时,如图2:
∵AB=8,BC=2,
∴AC=AB−BC=6,
∵点D为的AC中点,
∴AD=3,
∴BD=AB−AD=5;
综上所述:BD的长为3或5.
故答案为:3或5
【分析】先根据题意分类讨论:当点C在点B的右侧时,当点C在点B的左侧时,进而运用中点的性质进行线段的运算即可求解。
16.【答案】(2n+4)
【知识点】探索图形规律;用代数式表示图形变化规律
【解析】【解答】解:由题意得第1个图形中★的个数为:6=1×2+4;
第2个图形中★的个数为:8=2×2+4;
第3个图形中★的个数为:10=3×2+4;
…,
∴第n个图形中★的个数为:2n+4.
故答案为:(2n+4)
【分析】根据题意结合图片写出前3个图形中★的个数,进而即可得到第n个图形中★的个数。
17.【答案】解:原式=−15−21+8
=−36+8
=−28.
【知识点】有理数的加、减混合运算
【解析】【分析】运用有理数的加减混合运算结合题意即可求解。
18.【答案】解:原式=24×(−16)×32×(−34)
=24×16×32×34
=92.
【知识点】有理数的乘除混合运算
【解析】【分析】根据有理数的乘除混合运算结合题意即可求解。
19.【答案】解:−52+2×(−3)2−(−8)÷(−113)
=−25+2×9−8×34
=−25+18−6
=−13.
【知识点】有理数混合运算法则(含乘方)
【解析】【分析】根据有理数的混合运算(含乘方)即可求解。
20.【答案】解:原式=5x−y−6x+9y+x
=8y.
【知识点】整式的混合运算
【解析】【分析】根据整式的混合运算结合题意即可求解。
21.【答案】解:原式=2ab2−(3a2b−6a2b+2ab2+2)
=2ab2−3a2b+6a2b−2ab2−2
=(−3+6)a2b+(2−2)ab2−2
=3a2b−2,
当a=−1,b=3时,
原式=3×(−1)2×3−2
=3×1×3−2
=9−2
=7.
【知识点】利用整式的混合运算化简求值
【解析】【分析】先根据整式的混合运算进行化简,进而代入数值即可求解。
22.【答案】(1)解:见解析;如图,CD即为所求.
(2)解:见解析;如图,MN即为所求.
(3)∠MCE;∠NCB;>;<
【知识点】作图-平行线;作图-垂线;线段的长短比较;同旁内角
【解析】【解答】解:
(3)∠AEC的同旁内角为∠MCE.
∵AB//MN,
∴与∠ABC相等的角为∠NCB.
由图可知,CB>CE,CD
【分析】(1)根据作图-垂线结合题意画图即可求解;
(2)根据作图-平行线结合题意画图即可求解;
(3)根据同旁内角的定义、线段的比较、角结合题意填空即可求解。
23.【答案】解:∵∠AOC=40°,
∴∠AOD=180°−∠AOC=180°−40°=140°,
∵OE平分∠AOD,
∴∠EOD=12∠AOD=12×140°=70°,
∵OF⊥CD,
∴∠FOD=90°,
∴∠EOF=90°−∠EOD=90°−70°=20°.
【知识点】角的运算;角平分线的定义
【解析】【分析】先根据题意得到∠AOD的度数,进而根据角平分线的定义得到∠EOD的度数,再结合题意进行运算即可求解。
24.【答案】(1)解:+5−2+3+1+4−2+3−4−6=2,
则A站是一国街;
答:A站是一国街.
(2)解:(5+2+3+1+4+2+3+4+6)×1.5
=30×1.5
=45(千米),
答:这次李华志愿服务期间乘坐地铁行进的总路程约是45千米.
【知识点】有理数混合运算的实际应用
【解析】【分析】(1)根据有理数的加减混合运算结合正数与负数即可求解;
(2)根据题意进行有理数的混合运算即可求解。
25.【答案】证明:∵∠4=∠B(已知),
∴AB//DE(同位角相等,两直线平行).
∴∠2=∠3(两直线平行,内错角相等).
∵∠1=∠2(已知),
∴∠1=∠3(等量代换).
∴AD//GF(同位角相等,两直线平行).
∴∠ADF+∠GFD=180°(两直线平行,同旁内角互补).
又∵∠ADF=90°(已知),
∴∠GFD=90°.
∴GF⊥BC.
故答案为:DE;同位角相等,两直线平行;两直线平行,内错角相等;GF;同位角相等,两直线平行;180°;两直线平行,同旁内角互补.
【知识点】平行线的判定与性质
【解析】【分析】根据平行线的判定与性质结合题意即可求解。
26.【答案】(1)(12a+b);(a+2b−40)
(2)解:参加美术社团的人数为:220−a−(12a+b)−(a+2b−40)=(260−52a−3b)人,
答:参加美术社团的人数为(260−52a−3b)人;
(3)解:当a=60,b=25时,
260−52a−3b=260−52×60−3×25=260−150−75=35,
答:美术杜团的人数为35人.
【知识点】整式的混合运算;用代数式表示实际问题中的数量关系;求代数式值的实际应用
【解析】【解答】解:(1)由题意可知,参加朗诵社团的人数为(12a+b)人,参加舞蹈社团的人数为2(12a+b)−40=(a+2b−40)人,
故答案为:(12a+b),(a+2b−40);
【分析】(1)结合题意即可写出代数式;
(2)根据题意运用社团总人数减去其他社团的人数即可求解;
(3)根据题意代入数值即可求解。
27.【答案】(1)65
(2)解:过点E作EN//AB,如图②所示:
∵AB//CD,EN//AB,
∴AB//EN//AB,
∴∠B+∠BEN=180°,∠CEN=∠C,
∴∠B+∠BEN+∠CEN=180°+∠C,
∵∠BEC=∠BEN+∠CEN∴∠B+∠BEC=180°+∠C,
即∠B+∠BEC−∠C=180°;
(3)38
【知识点】角的运算;平行公理及推论;平行线的性质;角平分线的定义
【解析】【解答】解:(1)过点E作EM//AB,如图①所示:
∵AB//CD,EM//AB,
∴AB//EM//AB,
∴∠BEM=∠B,∠DEM=∠D,
∴∠BEM+∠DEM=∠B+∠D,
即∠BED=∠B+∠D,
∵∠B=25°,∠D=40°,
∴∠BED=25°+40°=65°,
故答案为:65.
(3)过点E作EK//AB,如图③所示:
设∠ECG=α,∠ABF=β,
∵CG平分∠DCE,
∴∠ECG=∠GCD=α,∠DCE=2α,
∵BF平分∠ABE,
∴∠ABE=2β,
∵AB//CD,FH//AB,EK//AB,
∴AB//EK//FH//AB,
∴∠BFH=∠ABF=β,∠ABE+∠BEK=180°,∠CEK=∠DCE=2α,∠GFH=∠GCD=α,
∴∠BEK=180°−∠ABE=180°−2β,
∵∠BEC=∠BEK+∠CEK=104°,
∴180°−2β+2α=104°,
即β−α=38°,
∴∠BFC=∠BFH−∠GFH=β−α=38°.
故答案为:38.
【分析】(1)过点E作EM//AB,进而根据平行公理推论即可得到AB//EM//AB,再根据平行线的性质得到∠BEM=∠B,∠DEM=∠D,进而结合题意进行角的运算即可求解;
(2)过点E作EN//AB,先根据平行公理推论得到AB//EN//AB,进而根据平行线的性质得到∠B+∠BEN=180°,∠CEN=∠C,再结合题意进行角的运算即可求解;
(3)过点E作EK//AB,设∠ECG=α,∠ABF=β,进而根据角平分线的性质得到∠ECG=∠GCD=α,∠DCE=2α,再结合题意运用平行公理推论得到AB//EK//FH//AB,从而根据平行线的性质得到∠BFH=∠ABF=β,∠ABE+∠BEK=180°,∠CEK=∠DCE=2α,∠GFH=∠GCD=α,进而结合题意进行角的运算即可求解。
28.【答案】(1)−10;−10+2t
(2)解:∵PA=2PB,AB=30cm,
∴PA=20cm,PB=10cm,
−10+2t=20,
解得:t=15,
点Q运动到的位置恰好是线段AB的中点,即NQ=20cm,
∴点Q的运动速度为20÷15=43(cm/s);
(3)解:点Q表示的数是35−3t,
①0
②9≤t时,−10+2t−(35−3t)=35,
当点Q运动到点M时停止运动,即t=15时,点Q停止运动,此时PQ=30cm,
还需P点运动5cm,5÷2=2.5(s),
∴t=15+2.5=17.5(s),
答:经过2秒或17.5秒P、Q两点相距35cm.
【知识点】一元一次方程的实际应用-行程问题;数轴上两点之间的距离;用代数式表示实际问题中的数量关系;折线数轴(双动点)模型
【解析】【解答】解:(1)∵AB=3AM,AM=2BN,AB=30cm,
∴AM=10cm,BN=5cm,
∵点A在原点,
∴点M表示的数是−10,点P表示的数是−10+2t,
故答案为:−10,−10+2t;
【分析】(1)先根据题意得到AM和BN的长,进而结合数轴即可求解;
(2)先根据题意得到PA和PB,进而即可列出一元一次方程,从而即可求出NQ,再结合题意即可求解;
(3)先根据题意得到点Q表示的数是35−3t,进而分类讨论:①0
2023-2024学年吉林省长春市南关区九上数学期末监测试题含答案: 这是一份2023-2024学年吉林省长春市南关区九上数学期末监测试题含答案,共7页。试卷主要包含了若,相似比为1等内容,欢迎下载使用。
吉林省长春市南关区2023一2024学年上学期八年级期末质量调研数学试题: 这是一份吉林省长春市南关区2023一2024学年上学期八年级期末质量调研数学试题,共6页。
吉林省长春市南关区2023届九年级下学期质量调研(中考二模)数学试卷(含解析): 这是一份吉林省长春市南关区2023届九年级下学期质量调研(中考二模)数学试卷(含解析),共25页。试卷主要包含了 不等式组的解集为, 分解因式等内容,欢迎下载使用。












