高三数学高考高分突破之概率统计专题31 自主招生问题（原卷版）50

这是一份高三数学高考高分突破之概率统计专题31 自主招生问题（原卷版）50，共6页。
（Ⅰ）求甲通过自主招生初试的概率；
（Ⅱ）试通过概率计算，分析甲、乙两人谁通过自主招生初试的可能性更大；
（Ⅲ）记甲答对试题的个数为，求的分布列及数学期望．
例2．甲、乙两位同学从共所高校中，任选两所参加自主招生考试（并且只
能选两所高校），但同学特别喜欢高校，他除选高校外，再在余下的所中随机选1所；同学乙
对所高校没有偏爱，在所高校中随机选2所． 若甲同学未选中高校且乙选中高校的概率为．
（1）求自主招生的高校数；
（2）记为甲、乙两名同学中未参加高校自主招生考试的人数，求的分布列和数学期望．
例3．有一名高二学生盼望2020年进入某名牌大学学习，假设该名牌大学有以下条件之一均可录取：①2020年2月通过考试进入国家数学奥赛集训队（集训队从2019年10月省数学竞赛一等奖中选拔）：②2020年3月自主招生考试通过并且达到2020年6月高考重点分数线，③2020年6月高考达到该校录取分数线（该校录取分数线高于重点线），该学生具备参加省数学竞赛、自主招生和高考的资格且估计自己通过各种考试的概率如下表
若该学生数学竞赛获省一等奖，则该学生估计进入国家集训队的概率是0.2.若进入国家集训队，则提前录取，若未被录取，则再按②、③顺序依次录取：前面已经被录取后，不得参加后面的考试或录取.（注：自主招生考试通过且高考达重点线才能录取）
（Ⅰ）求该学生参加自主招生考试的概率；
（Ⅱ）求该学生参加考试的次数的分布列及数学期望；
（Ⅲ）求该学生被该校录取的概率.
例4．大学先修课程，是在高中开设的具有大学水平的课程，旨在让学有余力的高中生早接受大学思维方式、学习方法的训练，为大学学习乃至未来的职业生涯做好准备.某高中成功开设大学先修课程已有两年，共有250人参与学习先修课程，这两年学习先修课程的学生都参加了高校的自主招生考试（满分100分），结果如下表所示：
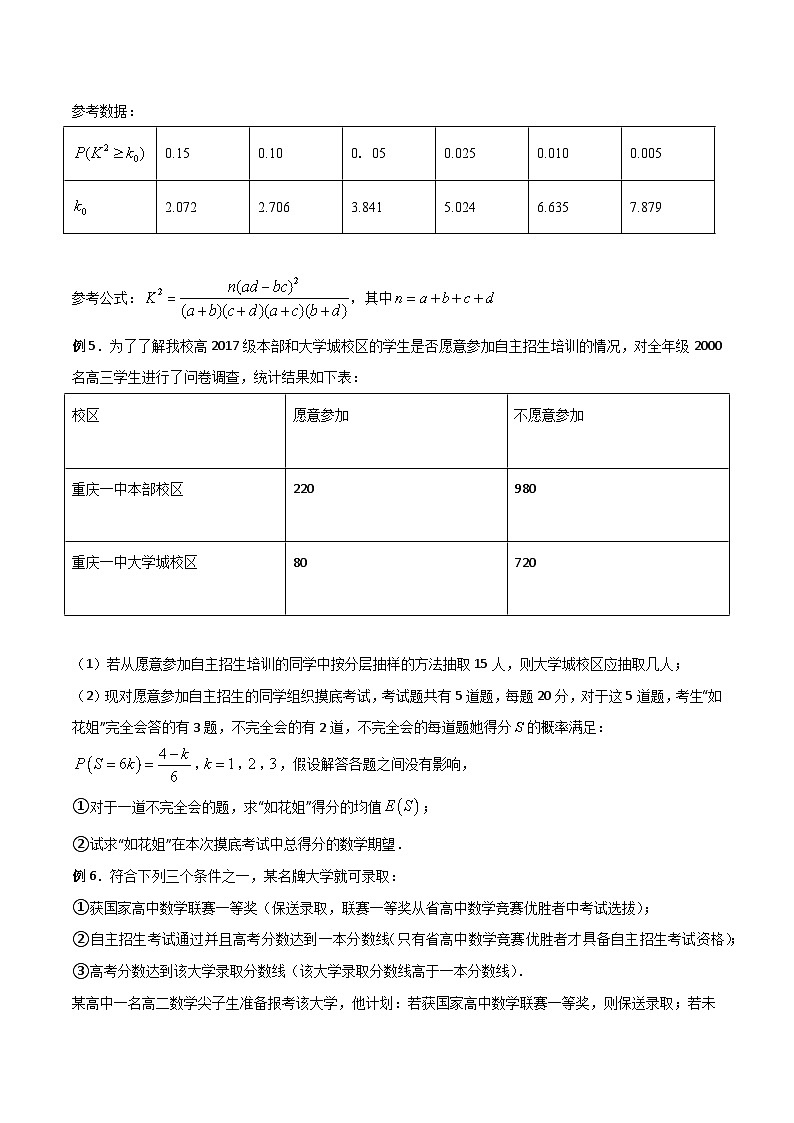
（Ⅰ）这两年学校共培养出优等生150人，根据下图等高条形图，填写相应列联表，并根据列联表检验能否在犯错的概率不超过0.01的前提下认为学习先修课程与优等生有关系？
（Ⅱ）已知今年全校有150名学生报名学习大学选项课程，并都参加了高校的自主招生考试，以前两年参加大学先修课程学习成绩的频率作为今年参加大学先修课程学习成绩的概率.
（ⅰ）在今年参与大学先修课程学习的学生中任取一人，求他获得高校自主招生通过的概率；
（ⅱ）某班有4名学生参加了大学先修课程的学习，设获得高校自主招生通过的人数为，求的分布列，试估计今年全校参加大学先修课程学习的学生获得高校自主招生通过的人数.
参考数据：
参考公式：，其中
例5．为了了解我校高2017级本部和大学城校区的学生是否愿意参加自主招生培训的情况，对全年级2000名高三学生进行了问卷调查，统计结果如下表：
（1）若从愿意参加自主招生培训的同学中按分层抽样的方法抽取15人，则大学城校区应抽取几人；
（2）现对愿意参加自主招生的同学组织摸底考试，考试题共有5道题，每题20分，对于这5道题，考生“如花姐”完全会答的有3题，不完全会的有2道，不完全会的每道题她得分的概率满足：，假设解答各题之间没有影响，
①对于一道不完全会的题，求“如花姐”得分的均值；
②试求“如花姐”在本次摸底考试中总得分的数学期望．
例6．符合下列三个条件之一，某名牌大学就可录取：
①获国家高中数学联赛一等奖（保送录取，联赛一等奖从省高中数学竞赛优胜者中考试选拔）；
②自主招生考试通过并且高考分数达到一本分数线（只有省高中数学竞赛优胜者才具备自主招生考试资格）；
③高考分数达到该大学录取分数线（该大学录取分数线高于一本分数线）．
某高中一名高二数学尖子生准备报考该大学，他计划：若获国家高中数学联赛一等奖，则保送录取；若未被保送录取，则再按条件②、条件③的顺序依次参加考试．
已知这名同学获省高中数学竞赛优胜奖的概率是0.9，通过联赛一等奖选拔考试的概率是0.5，通过自主招生考试的概率是0.8，高考分数达到一本分数线的概率是0.6，高考分数达到该大学录取分数线的概率是0.3．
（I）求这名同学参加考试次数的分布列及数学期望；
（II）求这名同学被该大学录取的概率．
例7．已知A,B,C,D,E五所高校举行自主招生考试，某同学决定按A,B,C,D,E的顺序参加考试，假设该同学参加每所高校的考试获得通过的概率均为13.
（1）如果该同学五所高校的考试都参加，求在恰有两所通过的条件下，不是连续两所通过的概率；
（2）如果该同学一旦通过某所高校的考试，就不再参加后面高校的考试，假设参加每所高校考试所需的费用均为162元，试求该同学参加考试所需费用X的数学期望.
例8．已知，，，…，等10所高校举行自主招生考试，某同学参加每所高校的考试获得通过的概率均为.
（1）如果该同学10所高校的考试都参加，恰有所通过的概率为，当为何值时，取得最大值；
（2）若，该同学参加每所高校考试所需的费用均为元，该同学决定按，，，…，顺序参加考试，一旦通过某所高校的考试，就不再参加其它高校的考试，否则，继续参加其它高校的考试，求该同学参加考试所需费用的分布列及数学期望.
例9．某中学的甲、乙、丙三名同学参加高校自主招生考试，每位同学彼此独立的从四所高校中选2所.
（Ⅰ）求甲、乙、丙三名同学都选高校的概率；
（Ⅱ）若已知甲同学特别喜欢高校，他必选校，另在三校中再随机选1所；而同学乙和丙对四所高校没有偏爱，因此他们每人在四所高校中随机选2所.
（ⅰ）求甲同学选高校且乙、丙都未选高校的概率；
（ⅱ）记为甲、乙、丙三名同学中选校的人数，求随机变量的分布列及数学期望.
例10．某中学的甲、乙、丙三名同学参加高校自主招生考试，每位同学彼此独立的从五所高校中任选2所．
（1）求甲、乙、丙三名同学都选高校的概率；
（2）若已知甲同学特别喜欢高校，他必选校，另在四校中再随机选1所；而同学乙和丙对五所高校没有偏爱，因此他们每人在五所高校中随机选2所．
（i）求甲同学选高校且乙、丙都未选高校的概率；
（ii）记为甲、乙、丙三名同学中选高校的人数，求随机变量的分布列及数学期望．
例11．现有甲、乙、丙三名学生参加某大学的自主招生考试，考试分两轮，第一轮笔试，第二轮面试，只有第一轮笔试通过才有资格进入第二轮面试，面试通过就可以在高考录取中获得该校的优惠加分，两轮考试相互独立.根据以往多次的模拟测试，甲、乙、丙三名学生能通过笔试的概率分别为0.4，0.8，0.5，能通过面试的概率分别为0.8，0.4，0.64.根据这些数据我们可以预测：
（1）甲、乙、丙三名学生中至少有两名学生通过第一轮笔试的概率；
（2）甲、乙、丙三名学生能获得该校优惠加分的人数的数学期望.
例12．中国大学先修课程,是在高中开设的具有大学水平的课程,旨在让学有余力的高中生早接受大学思维方式、学习方法的训练,为大学学习乃至未来的职业生涯做好准备，某高中每年招收学生1000人,开设大学先修课程已有两年,共有300人参与学习先修课程，两年全校共有优等生200人,学习先修课程的优等生有50人，这两年学习先修课程的学生都参加了考试,并且都参加了某高校的自主招生考试，结果如下表所示:
(1)填写列联表,并画出列联表的等高条形图,并通过图形判断学习先修课程与优等生是否有关系，根据列联表的独立性体验，能否在犯错误的概率不超过0.01的前提下认为学习先修课程与优等生有关系?
（2）已知今年有150名学生报名学习大学先修课程,以前两年参加大学先修课程学习成绩的频率作为今年参加大学先修课程学习成绩的概率.
①在今年参与大学先修课程的学生中任取一人,求他获得某高校自主招生通过的概率;
②某班有4名学生参加了大学先修课程的学习,设获得某高校自主招生通过的人数为,求的分布列,并求今年全校参加大学先修课程的学生获得大学自主招生通过的人数.
参考数据:
参考公式: ，期中，
省数学竞赛一等奖
自主招生通过
高考达重点线
高考达该校分数线
0.5
0.6
0.9
0.7
分数
人数
25
50
100
50
25
参加自主招生获得通过的概率
0.9
0.8
0.6
0.4
0.3
优等生
非优等生
总计
学习大学先修课程
250
没有学习大学先修课程
总计
150
0.15
0.10
0．05
0.025
0.010
0.005
2.072
2.706
3.841
5.024
6.635
7.879
校区
愿意参加
不愿意参加
重庆一中本部校区
220
980
重庆一中大学城校区
80
720